【机器学习】之第十一章——特征选择与稀疏学习
11.1、子集搜索与评价
对于一个学习任务来说,往往不是给定的属性集中所有的属性都很重要的,我们将对当前学习任务有用的属性称为“相关特征”,没什么用的属性称为“无关特征”。那么从给定的特征集合中选择出响应特征子集的过程就称为特征选择。
那么为什么要进行特征选择呢?具体可以认为有两个原因:
- 我们在现实任务重常常遇到维数灾难问题,也就是属性的数目过多,如果能够选择出重要的特征,那么维数灾难问题将大为减轻。
- 去除不相关特征往往会降低学习任务的难度
那么如何从初始的特征集合中选取出一个包含了所有重要信息的特征子集就是当前的问题。那么如果没有任何先验假设的话就相当于只能遍历所有可能的子集了,但这并不是我们想要的办法。可行的做法是产生一个“候选子集”,评价它的好坏,基于评价结果产生下一个“候选子集”,再评价再产生等等。
显然这就涉及到两个关键问题:
- 如何根据评价结果获取下一个候选特征子集
- 如何评价候选特征子集的好坏
第一个环节是“子集搜索”问题,例如每次不断选取单个当前表现最优的特征来加入特征子集中,直接再加入子集已经无法再次提升特征子集的表现就停止。这种称为前向搜索,还有后向搜索就是从全部的特征子集中来逐渐剔除。但是这两种方法主要是利用了贪心的思想,它们仅能够保证当前轮次是最优的,无法保证全局是最优的。
第二个环节是“子集评价”的问题,这种就有比较多样化的评价指标。
常见的特征选择方法可分为三大类:
- 过滤式
- 包裹式
- 嵌入式
11.2、过滤式
过滤式的方法是先对数据集进行特征选择,然后再来训练学习器。
著名过滤式特征选择方法设计了一个“相关统计量”来度量特征的重要性,该统计量是一个向量,其每个分量分别对应一个初始特征,而特征子集的重要性就是由子集中每个特征所对应的相关特征量分量之和来决定,最终通过一个阈值来筛选即可。
相关统计量的计算方法为:给定训练集 { ( x i , y i ) } \{(x_i,y_i)\} {(xi,yi)},对于每一个样本 x i x_i xi,先在它的同类样本中寻找其最近邻 x i , n h x_{i,nh} xi,nh,称为“猜中近邻”;再从其异类样本中寻找其最近邻 x i , n m x_{i,nm} xi,nm,称为“猜错近邻”。然后相关统计量对于属性j的分量为:
δ j = ∑ i − d i f f ( x i j , x i , n h j ) 2 + d i f f ( x i j , x i , n m j ) 2 \delta ^j=\sum_{i}-diff(x^j_i,x^j_{i,nh})^2+diff(x^j_i,x^j_{i,nm})^2 δj=i∑−diff(xij,xi,nhj)2+diff(xij,xi,nmj)2
其中如果该属性的分布是离散型,则如果两个类别相等就diff=0,否则为1;如果是连续性则 d i f f = ∣ x a j − x b j ∣ diff=\vert x^j_a-x^j_b \vert diff=∣xaj−xbj∣。注意需要先对属性进行标准化。
那么对于上述公式可以这样理解:如果该样本在属性j上与猜中近邻的距离,比其与猜错近邻的距离小,那么就认为该属性j对区分同类和异类样本有帮助,于是应该增大属性j所对应的统计量分量;反之则说明属性j其负面作用,于是减小属性j对应的统计量分量。因此最终得到的相关统计量分量数值越大,则说明该属性的分类能力越强。
上述计算方法是针对于二分类问题的,还可以进行拓展到多分类问题,即在同类(第k类)中找到最近邻之外,**在其余的每个类中都找到一个最近邻样本 x i , l , n m ( l = , 1 , 2 , . . , 类别数 ) x_{i,l,nm}(l=,1,2,..,类别数) xi,l,nm(l=,1,2,..,类别数)。那么:
δ j = ∑ i − d i f f ( x i j , x i , n h j ) 2 + ∑ l ≠ k ( p l × d i f f ( x i j , x i , l , n m j ) 2 ) \delta^j=\sum_{i}-diff(x^j_i,x^j_{i,nh})^2+\sum_{l\neq k}(p_l\times diff(x^j_i,x^j_{i,l,nm})^2) δj=i∑−diff(xij,xi,nhj)2+l=k∑(pl×diff(xij,xi,l,nmj)2)
其中 p l p_l pl为第 l l l类样本在数据集中所占的比例。
11.3、包裹式选择
包裹式特征选择最主要的特点在于其直接将最终要使用的学习器的性能作为特征子集的评价准则,也就是在先训练完分类器之后再根据该分类器来选择“量身定做”的特征子集。这就导致从最终学习器的性能来说,包裹式比过滤式的特征选择更好。
LVW是一种典型的包裹式特征选择方法,其算法描述如下:
需要注意的是由于LVW算法中特征子集搜索采取了随机策略,那么每次特征子集评价都需要训练学习器,因此计算开销会很大。
11.4、嵌入式选择与L1正则化
嵌入式特征选择的特点在于,其是将特征选择过程与学习器的训练过程融为一体,两者在同一个优化过程中完成,即在学习器训练过程中自动地进行了特征选择。
给定数据集,我们考虑最简单的线性回归模型,以平方误差为损失函数,其优化目标为:
min w ∑ i = 1 m ( y i − w T x i ) 2 \min_{w}\sum_{i=1}^m(y_i-w^Tx_i)^2 wmini=1∑m(yi−wTxi)2
为了防止其过拟合,通常我们会加入正则化项,若采用 L 2 L_2 L2范数正则化:
min w ∑ i = 1 m ( y i − w T x i ) 2 + λ ∥ w ∥ 2 2 \min_{w}\sum_{i=1}^m(y_i-w^Tx_i)^2+\lambda \Vert w \Vert^2_2 wmini=1∑m(yi−wTxi)2+λ∥w∥22
这也称为岭回归。
那么也可以将其中的 L 2 L_2 L2范数替换为 L p L_p Lp范数,例如使 p = 1 p=1 p=1,那么 L 1 L_1 L1范数为:
min w ∑ i = 1 m ( y i − w T x i ) 2 + λ ∥ w ∥ 1 \min_{w}\sum_{i=1}^m(y_i-w^Tx_i)^2+\lambda \Vert w \Vert_1 wmini=1∑m(yi−wTxi)2+λ∥w∥1
这称为LASSO回归。
上述提到的两个范数正则化都可以降低过拟合的风险,但 L 1 L_1 L1范数还有一个额外的好处为,它能够比 L 2 L_2 L2范数更容易获得稀疏解,也就是它求得的 w w w向量将含有更少的非零分量。
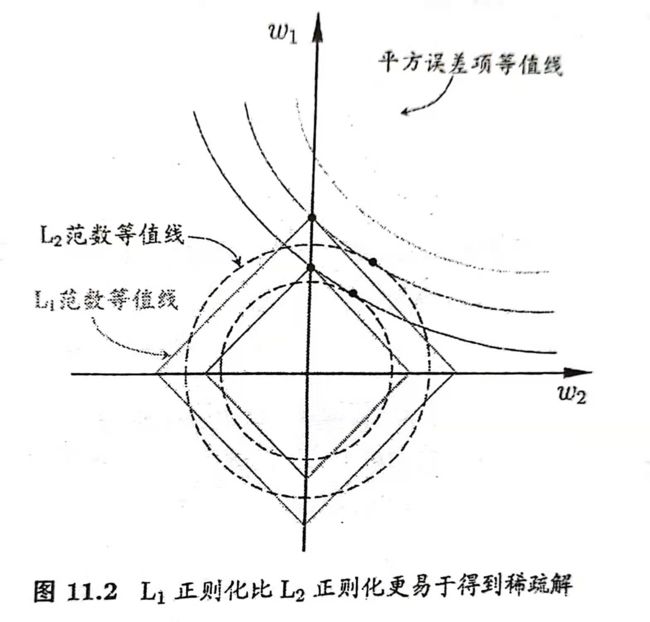
为了理解这一点可以通过下图来观察,假设有两个属性,那么在坐标轴中画出:
可以看到,采用 L 1 L_1 L1范数平方误差项等值线与正则化项等值线的交点通常出现在坐标轴上,即有某一个坐标为0,而采用 L 2 L_2 L2范数的话其交点通常出现在某个象限中。
那么 w w w得到稀疏解就意味着初始的d个特征中仅有对应着 w w w的非零分量的特征才会出现在最终模型中,于是求解 L 1 L_1 L1范数正则化的结果就是得到了仅采用一部分初始特征的模型;换而言之,这就是一种嵌入式的特征选择方法。