理解办公室政治就能理解神经网络
上节课我们讨论了神经元是如何工作的以及相关数学表示,这节课我们使用“人”话讨论神经元究竟是如何组成神经网络并且实现识别数字0和1。
先来个人脑神经网络示意图,
请问童鞋们能理解吗?
这样复杂的网络结构是很难理解的,学术上的说法是人大脑目前只开发了不到10%的功能吗?我们还是从简单的数字识别入手讲解人工智能神经网络吧。
先看下面这几张用12个灰黑、灰白方块组成的图
各位童鞋这些图片看上去是哪个数字呢?
产品黄此时说了句都是数字0呀,其他三位童鞋也纷纷点头。
老师接着又问哪还会不会有其他的表现形式呢?
产品黄立刻说到还有很多的比如下面这几张图都可以表示数字0。
此时应用张说道其实还会有很多其他组合模式,很难穷尽,这只是12个黑白方块,如果不只12个呢,怎么办,我们搞传统编程根本解决不了这个问题呀。
此时老师说道,是的,传统编程根本解决不了这个问题,是因为答案不标准呀。每个方块呢,我们都可以理解成是一个像素,而由12个二值像素组成的数字0,其组合模式也是多种多样的远远不只我们列出的这8种,对于这种没有标准答案,识别困难的问题,基于神经网络的深度学习技术是可以解决的。下面我们就通过一个三层的组织架构图来讲解神经网络是如何识别出数字0和1的。
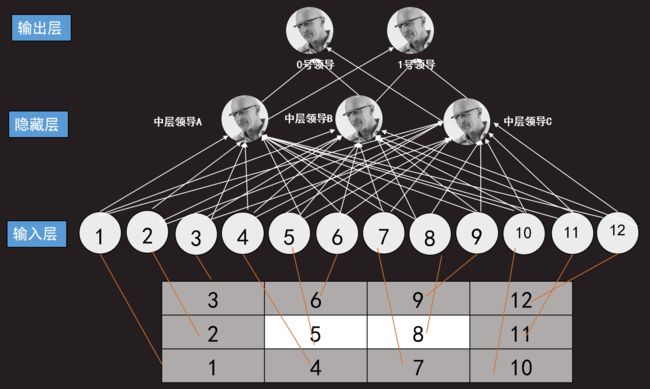
先看下图:
在图中所示的组织架构中,输入层即最下层有12个员工,他们分别代别代表数字0或1的12个黑白方块即12个黑白像素。输入层的12个员工就是负责把自已像素是什么颜色汇报给隐藏层的中层领导(神经元)A、B、C,隐藏层领导获得了12个手下是什么颜色的信息之后,进行整合,再把整合结果向输出层领导(神经元)汇报,由输出层0、1两个领导来判断数字究竟是“0”还是“1”。
现在的关键是隐藏层领导是如何进行整合,对于输出层领导做决策是决定性的。
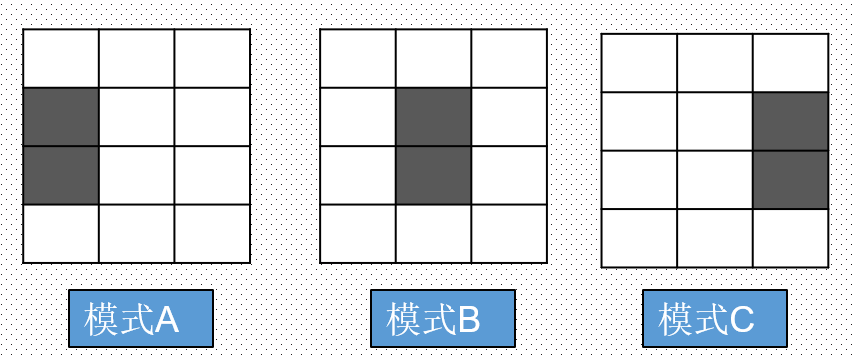
仔细来研究下发现隐藏层领导A、B、C有不同的喜好,他们分别喜欢下图所示的模式A、模式B、模式C的图案。
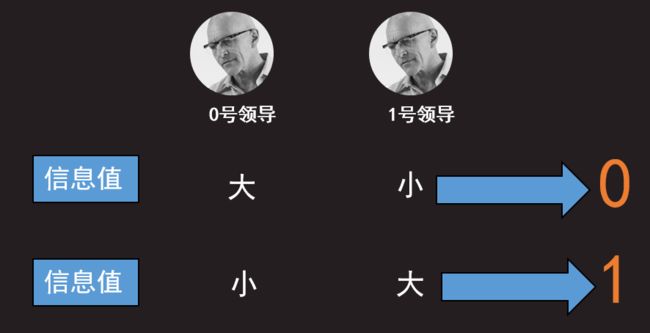
最上层的两个输出层领导,也是从下层的三个隐藏层ABC领导那里得到信息,并对信息进行整合,如果输出层0号领导整合后的信息比1号领导整合后的信息值大的话呢,就判定数字为0,反之就判定数字为1。
隐藏层领导A、B、C对模式有各自的偏好,和12个手下员工有不同的交情,领导A的偏好是之前的模式A,因此和4号还有7号关系好,因为模式A的4号像素与7号像素是黑色。中层领导的各自偏好见下图:
隐藏藏层领导A、B、C和输出层的领导也有着人际关系,由于某种关系输出层0号领导和隐藏层领导A、C关系较好,输出层1号领导与隐藏层B领导关系较好。注意看下图白色粗线代表关系好。
在把三个层次之间的关系说明白以后,我们来试着使用这个组织架构(神经网络)读入如下图所示的数字0,看看会产生什么反应呢?
变黑的4号和7号员工向性情相投的隐藏层领导A传递了较强的信息,变黑的6号9号员工也向向性情相投的隐藏层领导C传递了较强的信息,由于5号8号员工的颜色没有变黑,所以隐藏层领导B是没有得到较强的信息,这就直接导致了如下图所示的结果。
隐藏层领导A、B、C对接收到的信息进行整合之后向输出层领导汇报,输出层0号领导和1号领导根据关系好坏程度分别对信息整合,最后0号领导得到的信息值很强而1号领导得到信息值较弱,所以判断数字为0,具体过程如下图所示。
到此领导的神经网络终于推导出正确答案了。
现在想问下几位童鞋,学到这了,你们能否指出本节和神经元如何组成神经网络? 中的知识有哪些关联关系呢?
产品黄低头思考了一会儿说道,12个手下员工就是神经元的树突,最主要是在领导整合信息这一环节,领导就是细胞核,他们对于关系好的手下传过来的信息是比较信任,容易把这些信息整合向上汇报,关系好就是我们在神经元如何组成神经网络?一节中所说的权重,而对于关系较弱的手下传过来的信息,给出的权重就较低了。而隐藏层领导何时决定向上层传递信息,是由隐藏层领导根据自已实际情况来判断是否还需要把信息向上层汇报,而这个判断也就是我们在神经元如何组成神经网络?一节中所说的阀值了。
听完产品黄的回答,老师向产品黄竖起了大拇指。
此时算法刘问道:老师,隐藏层领导的人数到底如何确定呢?还有如果想把这个组织架构变成真正的神经网络,那么这个权重和阀值是应该能够量化确定下来的吧?这就好像一个能够正常运转的组织架构,必须要把相关的规章制度给确定下来,相关岗位的职责权给确定下来是一个道理吧?
老师听完算法刘的问题,说道这是个好问题呀,隐藏层领导的人数是需要人为来设置,那么根据什么来设置呢?最主要是根据需要识别的这个模式有多少种,种类越多,隐藏层的领导人数越多,这个其实也好理解,如果一个组织架构里面业务越多越复杂,那么呢中层领导也有可能就越多。
算法刘听完又接着问,那怎么知道这个模式会有多少呢?有时候根本不可能穷举所有的模式的,因为就像我们这个实际的12个像素识别手写数字的例子模式都有很多种,去穷举的话都代价很大。
老师听完算法刘的问题,说道这又是个好问题呀,是的,不可能穷举所有的模式,但是你可以先预估一下这个模式的复杂性设定一个隐层领导人数,然后根据实际的业务情况或者是说呢,你不断做实验反馈出来的一个结果来调整这个人数,比如说我们识别的这个准确率越来越高了,那当达到一个标准的时候,我们就不再调整这个人数了。
至于权重和阀值的确定,这是需要神经网络不断从数据中学习而来,比如说我们准备了几千张甚至上万张这种手写数字图片,那么这些数字图片里面所包含的模式特征就有很多,神经网络就可以通过这些模式特征和学习到什么样的权重和阀值适合这种模式特征,从而把权重和阀值给确定下来。举个例子来说,一个公司的业务在不断的扩充发展,那么它所包含的这个隐藏层的领导人数,还有整个的规章制度(权重和阀值)也是需要在不断的调整过程中的。
听完了老师的回答之后,此时应用张问道:刚才的问题都是在说隐藏层的领导人数和权重阀值,这个我听懂了,那输出层的领导人数又怎么来确定呢?难道输出层的领导人数就是根据你要识别的技术有多少个你就有多少人吗?假如我们要识别0~9的10个数字就要有10个领导吗?
老师听完应用张的问题,说道这又是个好问题呀,看看样子同学们都是非常认真的在听课呀,否则提不出这些问题。虽然从理论上来说,可以用一个领导就可以解决多分类的问题,可这会使算法变复杂,在数学上进行表达非常的麻烦,不直观不美,所以在实践的过程中就是按照应用张提出来的解决办法,既有多少分类问题,我们就设多少个输出层领导。
课程到此,大家还有什么问题没有?没有问题我们就结束这节课程的讲解了。
算法刘问道,整个课程讲下来,是比较通俗易懂,也很容易听懂。但神经网络究竟如何学到这个权重和阀值好像还不是很清楚?
老师听完算法刘的问题,说道算法刘真不愧是搞算法的,这种打破砂锅问到底的精神值得点赞。神经网络如何学习到这个权重和阀值其实是通过很多算法来进行学习的,比如说损失函数中入门性的算法最小二乘法、优化算法梯度下降,激活函数算法、反向传播算法,这些算法的学习又要用到很多相应的数学知识,比如说线性代数里面的矩阵分解,方程组求解、高等数学中的求导,还有概率论中的极大似然、概率分布等等等,这些知识我们都会在后续的课程中一边学习AI的实例一边来讲解。
问题,这节课就到此结束了,如果后续还有什么问题的话,欢迎大家在课程的评论区中留言咨询就行了。
再次提示如果童鞋们忘记了权重和阀值是什么含义的话,最好是回看我们在神经元如何组成神经网络?这一章节。
最后还是给大家留个作业吧。
作业:请使用本章给出的领导神经网络,画出如下图数字1的识别过程?
课程结束时,如果觉得课程GET到你了,请一键三连哟!
为了奖励阅读完成你,给出个彩蛋,推荐购买《深度学习的数学》,本课程中很多知识案例都是取材于此本书中,包括本节的知识。