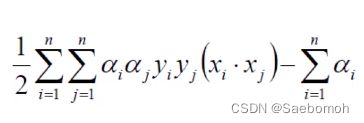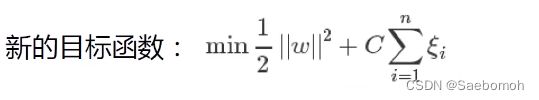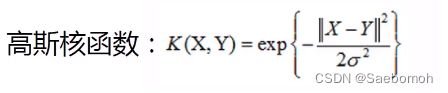支持向量机
原理推导:
1.支持向量机要解决的问题
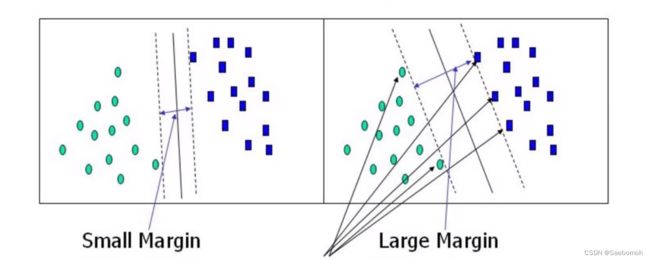
决策边界:
选出来的边界距离两边最近点的距离达到最大,最大间隔。
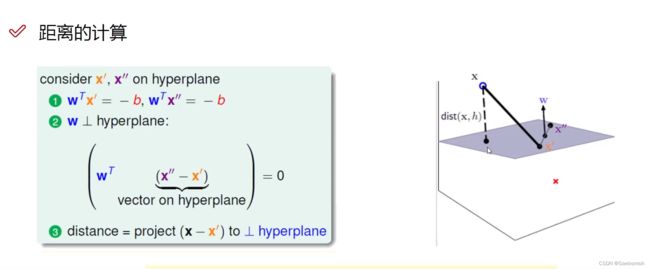
2.距离与数据的定义
找出最近点到面的距离推导:
数据定义:
3.目标函数推导
4.拉格朗日化简最终函数
有约束条件,又要求极值问题,所以引入拉格朗日函数,简单来说拉格朗日就是让目标方程与一个参数方程联系,再有当前方程与参数方程联系,最后再让目标方程和当前方程联系,做一个中介人的作用。
最后求偏导即可 ,最终方程
6.软间隔优化
软间隔︰有时候数据中有一些噪音点,如果考虑它们,咱们的线就不太好了。
之前的方法要求要把两类点完全分得开,这个要求有点过于严格了,我们来放松一点!
为了解决该问题,引入松弛因子
y,(w·x,+b)>1一![]()
C是我们应该设定的参数,这个值实验用到
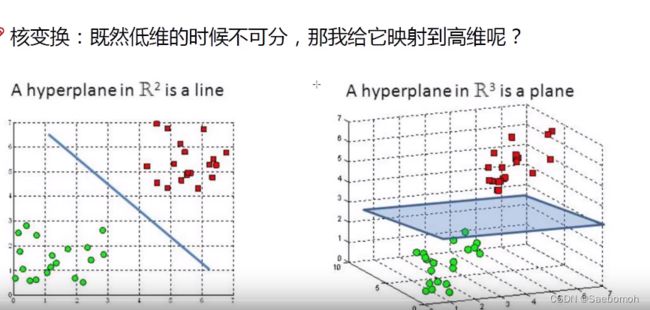
7.核函数
主要思想就是 将 低纬度的转换成高纬度的,如果从低纬度变换到高纬度再进行求解,时间复杂度会很大,若我先在低纬度求解后映射到高纬度,时间复杂度会大大缩短!
实验中用到
高斯核函数
代码部分:
线性可分支持向量机学习算法--最大间隔法
from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt
# 构建正态分布来产生数字,20行2列*2
train_x = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
# 构建 20个class0,20个class1
label_y = [0] * 20 + [1] * 20
# svm设置:
clf = svm.SVC(kernel='linear')
clf.fit(train_x, label_y)
# 获取weights
weights = clf.coef_[0]
rate = -weights[0] / weights[1] # 斜率
# 画图划线
xx = np.linspace(-5, 5) # (-5,5)之间x的值
yy = rate * xx - (clf.intercept_[0]) /weights[1] # xx带入y,截距
# 画出与点相切的线
b = clf.support_vectors_[0]
#yy_down 是线 yy的下边的边界线
yy_down = rate * xx + (b[1] - rate* b[0])
b = clf.support_vectors_[-1]
#yy_up 是线 yy的上边的边界线
yy_up =rate * xx + (b[1] - rate * b[0])
# 测试
for i in range(20):
test_x = np.random.randn(1, 2) * 10
print('测试:点({},{}) 所属类别{}'.format(test_x[0][0],test_x[0][1], clf.predict(test_x)))
plt.figure(figsize=(8, 4))
plt.plot(xx, yy)
#绘制左上角的线
plt.plot(xx, yy_up)
#绘制 左下角的线
plt.plot(xx, yy_down)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80)
plt.scatter(train_x[:, 0], train_x[:, 1], c=label_y, cmap=plt.cm.Paired) # [:,0]列切片,第0列
plt.axis('tight')
plt.show()
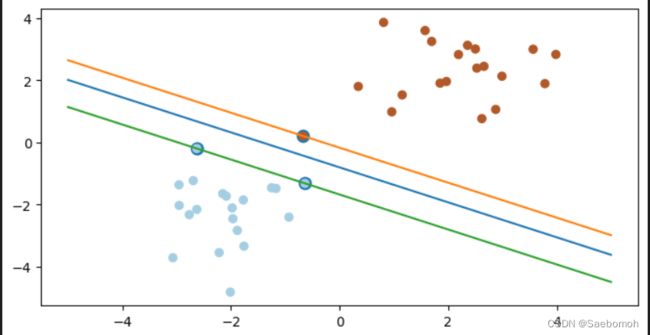
结果展示:
两个样本类型 ,上面只有三个点与求解的优化问题有关,它们就叫做支持向量。可以看出效果还不错
2.非线性支持向量机学习算法
输入:训练集T={(x1,y1),(x2,y2),...,(xN,yN)}
输出:分类决策函数
第一步:选取适当的核函数K(x,z)和适当的参数C,构造并求解最优化问题,求得最优化问题的解
第二步:选择α的一个正分量
第三步:构造决策函数
代码部分:
import matplotlib.pyplot as plt
import numpy as np
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
from sklearn import datasets
from tensorflow.python.framework import ops
sess = tf.compat.v1.Session()
#加载数据
# iris.数据 [(Sepal Length, Sepal Width, Petal Length, Petal Width)]
iris = datasets.load_iris()
x_vals = np.array([[x[0], x[3]] for x in iris.data])
y_vals = np.array([1 if y==0 else -1 for y in iris.target])
class1_x = [x[0] for i,x in enumerate(x_vals) if y_vals[i]==1]
class1_y = [x[1] for i,x in enumerate(x_vals) if y_vals[i]==1]
class2_x = [x[0] for i,x in enumerate(x_vals) if y_vals[i]==-1]
class2_y = [x[1] for i,x in enumerate(x_vals) if y_vals[i]==-1]
#声明变量
# 批量大小
batch_size = 150
# 初始化占位符
x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32)
y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)
prediction_grid = tf.placeholder(shape=[None, 2], dtype=tf.float32)
# 创建变量
b = tf.Variable(tf.random_normal(shape=[1,batch_size]))
#高斯核函数
# 高斯核函数 (RBF)
gamma = tf.constant(-50.0)
sq_vec = tf.multiply(2., tf.matmul(x_data, tf.transpose(x_data)))
my_kernel = tf.exp(tf.multiply(gamma, tf.abs(sq_vec)))
## SVM模型的损失函数
first_term = tf.reduce_sum(b)
b_vec_cross = tf.matmul(tf.transpose(b), b)
y_target_cross = tf.matmul(y_target, tf.transpose(y_target))
second_term = tf.reduce_sum(tf.multiply(my_kernel, tf.multiply(b_vec_cross, y_target_cross)))
loss = tf.negative(tf.subtract(first_term, second_term))
rA = tf.reshape(tf.reduce_sum(tf.square(x_data), 1),[-1,1])
rB = tf.reshape(tf.reduce_sum(tf.square(prediction_grid), 1),[-1,1])
pred_sq_dist = tf.add(tf.subtract(rA, tf.multiply(2., tf.matmul(x_data, tf.transpose(prediction_grid)))), tf.transpose(rB))
pred_kernel = tf.exp(tf.multiply(gamma, tf.abs(pred_sq_dist)))
#声明预测时所采用的的很函数RBF
prediction_output = tf.matmul(tf.multiply(tf.transpose(y_target),b), pred_kernel)
prediction = tf.sign(prediction_output-tf.reduce_mean(prediction_output))
accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.squeeze(prediction), tf.squeeze(y_target)), tf.float32))
# 优化器的设置
my_opt = tf.train.GradientDescentOptimizer(0.01)
train_step = my_opt.minimize(loss)
# 初始化变量
init = tf.global_variables_initializer()
sess.run(init)
#开始训练
# 开始训练
loss_vec = []
batch_accuracy = []
for i in range(300):
rand_index = np.random.choice(len(x_vals), size=batch_size)
rand_x = x_vals[rand_index]
rand_y = np.transpose([y_vals[rand_index]])
sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})
temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})
loss_vec.append(temp_loss)
acc_temp = sess.run(accuracy, feed_dict={x_data: rand_x,
y_target: rand_y,
prediction_grid: rand_x})
batch_accuracy.append(acc_temp)
if (i + 1) % 75 == 0:
print('Step #' + str(i + 1))
print('Loss = ' + str(temp_loss))
#构建绘图时的数据点
# Create a mesh to plot points in
x_min, x_max = x_vals[:, 0].min() - 1, x_vals[:, 0].max() + 1
y_min, y_max = x_vals[:, 1].min() - 1, x_vals[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
grid_points = np.c_[xx.ravel(), yy.ravel()]
[grid_predictions] = sess.run(prediction, feed_dict={x_data: x_vals,
y_target: np.transpose([y_vals]),
prediction_grid: grid_points})
grid_predictions = grid_predictions.reshape(xx.shape)
#绘制图形
plt.contourf(xx, yy, grid_predictions, cmap=plt.cm.Paired, alpha=0.8)
plt.plot(class1_x, class1_y, 'ro', label='I. setosa')
plt.plot(class2_x, class2_y, 'kx', label='Non setosa')
plt.title('Gaussian SVM Results on Iris Data')
plt.xlabel('Petal Length')
plt.ylabel('Sepal Width')
plt.legend(loc='lower right')
plt.ylim([-0.5, 3.0])
plt.xlim([3.5, 8.5])
plt.show()
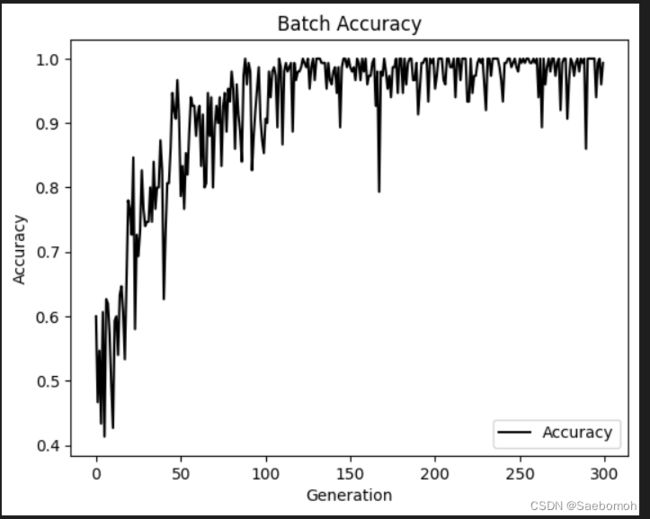
# Plot batch accuracy
plt.plot(batch_accuracy, 'k-', label='Accuracy')
plt.title('Batch Accuracy')
plt.xlabel('Generation')
plt.ylabel('Accuracy')
plt.legend(loc='lower right')
plt.show()
# Plot loss over time
plt.plot(loss_vec, 'k-')
plt.title('Loss per Generation')
plt.xlabel('Generation')
plt.ylabel('Loss')
plt.show()
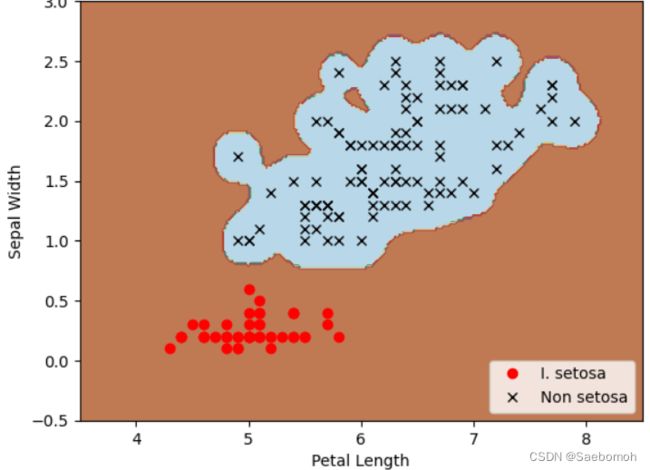
横轴是花瓣长度,纵轴是刚毛宽度,背景用颜色填充。从整体来说这个模型可能优点过拟合,
可以看出来,这个实验测试数据有点过拟合了,误差突然变大在中间时候 。这个采用的是高斯核函数进行的,可以看出他能够分离出非线性的边界。
总结
SVM中利用了核函数的计算技巧,大大降低了计算复杂度:
增加gamma v 使高斯曲线变窄,因此每个实例的影响范围都较小:决策边界最终变得更不规则,在个别实例周围摆动。
减少gamma y使高斯曲线变宽,因此实例具有更大的影响范围,并且决策边界更加平滑。
在软间隔中,我们可以知道C值大小影响着整个决策函数,若C值很大,我们不允许有任何出错,这样松弛因子就很小几乎没有很容易受噪声影响,若C值很小,则我们可以允许较大的误差范围,因此C值得选择十分重要!
参考:
1.CyberToday 公众号
2.唐宇迪精讲机器学习