人工晶状体计算——人工智能算法（R语言）

人工晶状体计算——人工智能算法（R语言）

1. 准备数据

2. 建立模型

2.1 方法1

2.2 方法2

---

1. 准备数据

准备数据Data.xlsx，示例如图

 

Age	AL	ACD	K1	K2	WTW	LT	Ref	IOLPower
68.00	22.68	2.21	42.44	42.75	11.20	4.82	-1.13	26.50
62.00	23.79	3.42	43.93	45.51	11.70	4.49	-0.11	19.50
62.00	23.82	3.12	44.08	44.53	12.00	4.90	-0.86	21.00
68.00	22.56	2.30	42.65	43.13	11.00	4.65	-0.37	25.50
73.00	23.50	2.38	43.43	43.84	11.40	4.85	-0.26	21.50
74.00	23.09	2.91	43.86	44.74	11.90	4.45	-0.53	23.00
73.00	24.61	3.57	41.70	42.23	11.90	3.49	-0.80	21.00
64.00	22.47	2.89	46.63	48.01	11.10	4.41	-0.52	21.00
63.00	21.35	2.67	43.89	44.53	12.20	4.68	-0.58	29.50

2. 建立模型

2.1 方法1

直接建立Age,AL,ACD,K1,K2,WTW,LT,Ref与IOLPower之间的关系

将使用多种人工智能模型，最后将表现最优的三种叠加在一起。

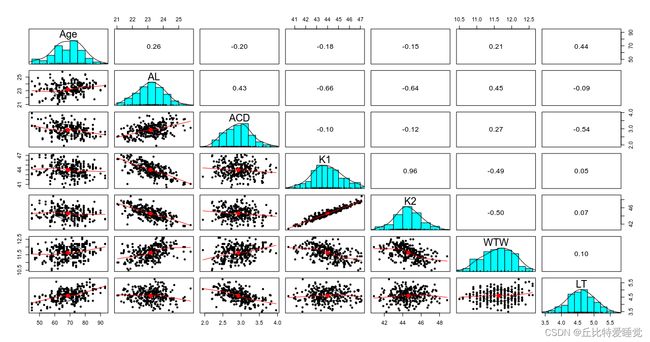
开始先看一下各自变量之间的相关性：

可以看到自变量之间还是有一定相关性的，比如LT(Lens Thickness)与Age正相关，ACD与AL正相关等。

rm(list=ls())
# load libraries
library(caret)
library(corrplot)
library(tidyverse)
library(xlsx)
# Split out validation dataset
set.seed(123)
df <- read.xlsx("./Data.xlsx",sheetName ="Sheet1",stringsAsFactors = FALSE)
str(df)
names(df)<-c("Age","AL","ACD","K1","K2","WTW","LT","IOLPower","Ref")
cor(df[c("Age","AL","ACD","K1","K2","WTW","LT")])
pairs(df[c("Age","AL","ACD","K1","K2","WTW","LT")])
# more informative scatterplot matrix
library(psych)
pairs.panels(df[c("Age","AL","ACD","K1","K2","WTW","LT")])

train.idx <- sample(1:nrow(df), 0.7*nrow(df))
train.df <- as_tibble(df[train.idx,])
test.df <- as_tibble(df[-train.idx,])
train_x = train.df %>% select(-'IOLPower')
train_y = train.df[,'IOLPower']
test_x = test.df %>% select(-'IOLPower')
test_y = test.df[,'IOLPower']
# Run algorithms using 10-fold cross validation
control <- trainControl(method="repeatedcv", number=10, repeats=3, search="random")
metric <- "RMSE"
# lm
set.seed(123)
fit_lm <- train(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref, data=train.df, method="lm",
metric=metric, preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_lm
# SVM
set.seed(123)
fit_svm <- train(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.df,
method="svmRadial", metric=metric, preProc=c("center", "scale"), tuneLength=15,
trControl=control)
fit_svm

# ANNs
fit_nnet <- train(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.df, method="nnet",
                  metric=metric, preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_nnet
if(FALSE)
{
  pred_Power <-predict(fit_nnet,test_x)
  print(pred_Power)
  err<- test_y$IOLPower-pred_Power
  print(err)
  plot(err)
}

# random forest
set.seed(123)
fit_rf <- train(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref, data = train.df, method="rf",
metric=metric, preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_rf
# CART
set.seed(123)
fit_cart <- train(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.df, method="rpart",
metric=metric,preProc=c("center", "scale"),tuneLength=15, trControl=control)
fit_cart
# kNN
set.seed(123)
fit_knn <- train(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.df, method="knn",
metric=metric, preProc=c("center", "scale"),tuneLength=15, trControl=control)
fit_knn
#MARS
set.seed(123)
fit_MARS<- train(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.df,
method="earth", metric=metric, preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_MARS
# GBM
set.seed(123)
fit_gbm <- train(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref, data = train.df, method =
"gbm",metric=metric,preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_gbm
#cubist
set.seed(123)
trControl=control
fit_cubist<- train(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref, data = train.df, method =
                     "cubist",metric=metric,preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_cubist
# Compare algorithms
results <- resamples(list(LM = fit_lm, CART = fit_cart, KNN= fit_knn, RF = fit_rf, SVR = fit_svm,
GBM = fit_gbm, MARS= fit_MARS, Cubist = fit_cubist,ANNs=fit_nnet))
summary(results)
dotplot(results)
# Stacking
library(caretEnsemble)
set.seed(123)

allModels <- caretList(IOLPower ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.df,trControl
= trainControl("repeatedcv", number = 10, repeats = 3, search="random",verboseIter = T),metric =
"RMSE", tuneList = list(cubist = caretModelSpec(method = "cubist", tuneLength = 15, preProc =
c("center","scale")),svmRadial = caretModelSpec(method = "svmRadial", tuneLength = 15, preProc
= c("center","scale")),Earth = caretModelSpec(method = "earth", tuneLength = 15, preProc =
c("center","scale"))))

bwplot(resamples(allModels), metric = "RMSE")
summary(allModels)
# Stack with lm
set.seed(123)
stack <- caretStack(allModels, metric = "RMSE", method = "lm", tuneLength = 10,trControl =
trainControl("repeatedcv", number = 5, repeats = 3, verboseIter = T))
summary(stack)
print(stack)

if(TRUE){
  ggplot(varImp(fit_lm))
  pred_Power <-predict(stack,test_x)
  print(pred_Power)
  plot(pred_Power)
  pred_err <- test_y$IOLPower - pred_Power
  print(pred_err)
  summary(pred_err)
  plot(pred_err)
}

运行结果误差还是很小的。

2.2 方法2

结合光学公式与人工智能（此法源自中山的一篇论文）

光学人工晶体计算公式如下

Power =1336 / (AL- ELP) - (1336/(1336 /(1000 /(1000 /Ref-12)+K)-ELP))

临床实践中最难的就是预测ELP(Effective Lens Position，有效人工晶状体位置，个人觉得"等效人工晶状体位置"这个翻译可能更好)，以下代码中Ratio指

Ratio =(ELP-ACD)/LT

下面代码的各个模型都是为了预测这个Ratio，最后求得ELP，然后代入上述光学计算公式中得到最后的人工晶状体度数。

if (TRUE){
  rm(list=ls())
  library(xlsx)
  data <- read.xlsx("./Data.xlsx",sheetName ="Sheet1",stringsAsFactors = FALSE)
  f<-function(ELP,AL,K,Ref,P)
  {1336 / (AL- ELP) - (1336/(1336 /(1000 /(1000 /Ref-12)+K)-ELP))-P}
  root<-c()
  
  for(i in 1:nrow(data)){
    root[i]<-uniroot(f,c(0,20),AL=data$AL[i],K=(data$K1[i]+data$K2[i])/2,R=data$Ref[i],P=data$IOLPower[i])$root
  }
  root
  data$ELP <-root
  Ratio <- (data$ELP-data$ACD)/data$LT
  Ratio
  data$Ratio<-Ratio
  PowerCalc<-function(ELP,AL,K,Ref)
  {1336 / (AL- ELP) - (1336/(1336 /(1000 /(1000 /Ref-12)+K)-ELP))}
  P<-PowerCalc(data$ELP,data$AL,(data$K1+data$K2)/2,data$Ref)
  P
  options(scipen = 100) #小数点后100位不使用科学计数法
  err <- data$IOLPower - P
  summary(err)
  plot(err)
}


library(caret)
library(corrplot)
library(tidyverse)
library(xlsx)
# Split out validation dataset
set.seed(123)
cor(data[c("Age","AL","ACD","K1","K2","WTW","LT")])
pairs(data[c("Age","AL","ACD","K1","K2","WTW","LT")])
# more informative scatterplot matrix
library(psych)
pairs.panels(data[c("Age","AL","ACD","K1","K2","WTW","LT")])

train.idx <- sample(1:nrow(data), 0.7*nrow(data))
train.data <- as_tibble(data[train.idx,])
test.data <- as_tibble(data[-train.idx,])
train_x = train.data %>% select(-'Ratio')
train_y = train.data[,'Ratio']
test_x = test.data %>% select(-'Ratio')
test_y = test.data[,'Ratio']
# Run algorithms using 10-fold cross validation
control <- trainControl(method="repeatedcv", number=10, repeats=3, search="random")
metric <- "RMSE"
# lm
set.seed(123)
fit_lm <- train(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref, data=train.data, method="lm",
                metric=metric, preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_lm
# SVM
set.seed(123)
fit_svm <- train(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.data,
                 method="svmRadial", metric=metric, preProc=c("center", "scale"), tuneLength=15,
                 trControl=control)
fit_svm
plot(fit_svm)
# ANNs
fit_nnet <- train(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.data, method="nnet",
                  metric=metric, preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_nnet
if(TRUE)
{
  pred <-predict(fit_nnet,test_x)
  print(pred)
  err<- test_y$Ratio-pred
  print(err)
  plot(err)
}

# random forest
set.seed(123)
fit_rf <- train(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref, data = train.data, method="rf",
                metric=metric, preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_rf
# CART
set.seed(123)
fit_cart <- train(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.data, method="rpart",
                  metric=metric,preProc=c("center", "scale"),tuneLength=15, trControl=control)
fit_cart
# kNN
set.seed(123)
fit_knn <- train(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.data, method="knn",
                 metric=metric, preProc=c("center", "scale"),tuneLength=15, trControl=control)
fit_knn
#MARS
set.seed(123)
fit_MARS<- train(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.data,
                 method="earth", metric=metric, preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_MARS
# GBM
set.seed(123)
fit_gbm <- train(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref, data = train.data, method =
                   "gbm",metric=metric,preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_gbm
#cubist
set.seed(123)
trControl=control
fit_cubist<- train(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref, data = train.data, method =
                     "cubist",metric=metric,preProc=c("center", "scale"), tuneLength=15, trControl=control)
fit_cubist
# Compare algorithms
results <- resamples(list(LM = fit_lm, CART = fit_cart, KNN= fit_knn, RF = fit_rf, SVR = fit_svm,
                          GBM = fit_gbm, MARS= fit_MARS, Cubist = fit_cubist,ANNs=fit_nnet))
summary(results)
dotplot(results)
# Stacking
library(caretEnsemble)
set.seed(123)

allModels <- caretList(Ratio ~ Age+AL+ACD+K1+K2+WTW+LT+Ref,data=train.data,trControl
                       = trainControl("repeatedcv", number = 10, repeats = 3, search="random",verboseIter = T),metric =
                         "RMSE", tuneList = list(cubist = caretModelSpec(method = "cubist", tuneLength = 15, preProc =
                                                                           c("center","scale")),svmRadial = caretModelSpec(method = "svmRadial", tuneLength = 15, preProc
                                                                                                                           = c("center","scale")),Earth = caretModelSpec(method = "earth", tuneLength = 15, preProc =
                                                                                                                                                                           c("center","scale"))))

bwplot(resamples(allModels), metric = "RMSE")
summary(allModels)
# Stack with lm
set.seed(123)
stack <- caretStack(allModels, metric = "RMSE", method = "lm", tuneLength = 10,trControl =
                      trainControl("repeatedcv", number = 5, repeats = 3, verboseIter = T))
summary(stack)
print(stack)

if(TRUE){
  ggplot(varImp(fit_nnet))
  pred_Ratio <-predict(stack,test_x)
  print(pred_Ratio)
  plot(pred_Ratio)
  pred_err1 <- test_y$Ratio - pred_Ratio
  print(pred_err1)
  summary(pred_err1)
  plot(pred_err1)
  ELPCalc<-function(Ratio,LT,ACD){Ratio*LT+ACD}
  ELP = ELPCalc(pred_Ratio,test_x$LT,test_x$ACD)
  Pred_Power<-PowerCalc(ELP,test_x$AL,(test_x$K1+test_x$K2)/2,test_x$Ref)
  Pred_err2<-test_x$IOLPower - Pred_Power
  summary(Pred_err2)
  plot(Pred_err2)
}

复现论文也算勉强成功，但是样本量太少，暂无法比较两种方法的优劣。