多分类逻辑回归 MNLogit python

引言

相比二分类Logistics回归的广泛应用与大量例子帖子，多分类Logistics回归的python实现的帖子则数量有限，特此记录一下。

本文介绍了多分类Logistics回归的统计方面的应用，更加关注于统计分析中的模型显著性、变量显著性、变量系数等问题，使用的是python的statsmodels库中的MNLogit函数。若更加注重预测的准确性，或构造更加良好的预测模型，建议尝试使用sklearn库中的相关函数。

实例及python实现

数据集

[数据集链接]
(https://download.csdn.net/download/weixin_45272208/86402859)

数据集基本情况如下：共5个特征变量（gre(考试成绩)，gpa(平均成绩点)，gender(性别)，prestige(学校威望)），1个分类变量admit(是否录取)。其中admit有3种取值：2表示录取，1表示待考虑，0表示不录取。gender（性别）0代表女性，1代表男性。prestige(学校威望)取值共1、2、3、4，4种情况，值越大，表示学校声望越差。（zhihu上的数据集做了点小改动）

import numpy as np
import pandas as pd
import os

import warnings
warnings.filterwarnings('ignore')
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = 'all'       # 多行结果同时输出

os.chdir(r'D:\Work\data')    # 设置数据集所在路径
data = pd.read_csv('graduate.csv')

查看数据情况

data.info()
data.head()
data['admit'].value_counts()

0、1、2三类分别有39、234、127个人

Logistics回归

X = data.drop(['admit'], axis=1, inplace=False)
X['intercept'] = 1.0     # 添加截距列
Y = data['admit']

from statsmodels.discrete.discrete_model import MNLogit
model_LR = MNLogit(Y,X,missing='drop').fit()
model_LR.summary()	# 查看结果
model_LR.params		# 查看参数的系数

输出结果

Optimization terminated successfully.意味着迭代成功，若超过迭代次数失败，则可尝试在fit()中添加 maxiter = n ，n为最大迭代次数，从而迭代多次获得结果。

还可以用summary2()查看模型结果。

LLR p-value即为模型的p值，可以看出模型显著。P>|z|为参数的p值，参数部分显著。

参数系数

模型评价

Precision、Recall、f1_score

from sklearn.metrics import accuracy_score, roc_auc_score, roc_curve, precision_score, recall_score, f1_score, auc
from sklearn.preprocessing import label_binarize 
from itertools import cycle

# Precision Recall 和 F1
nb_classes = 3          # 设置分类数

y_pred = model_LR.predict()      # 自我预测，得到预测为各类的概率
y_pred_max = [np.argmax(y) for y in y_pred]   # 取出y中元素最大值所对应的索引
y_true = Y

y_pred_b = label_binarize(y_pred_max, classes=[i for i in range(nb_classes)])    # binarize the output
y_true_b = label_binarize(y_true, classes=[i for i in range(nb_classes)])    # binarize the output

precision = precision_score(y_true_b, y_pred_b, average='micro')
recall = recall_score(y_true_b, y_pred_b, average='micro')
f1_score = f1_score(y_true_b, y_pred_b, average='micro')

print("Precision_score:",precision)
print("Recall_score:",recall)
print("F1_score:",f1_score)

因为是多分类，这里我用是micro方法求得整个模型的平均的Precision、Recall和fi_score。在多分类中，这三个值是相同的。

ROC曲线及AUC

import matplotlib.pyplot as plt

Y_valid = y_true_b
Y_pred = y_pred_b

fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(nb_classes):
    fpr[i], tpr[i], _ = roc_curve(Y_valid[:, i], Y_pred[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

fpr["micro"], tpr["micro"], _ = roc_curve(Y_valid.ravel(), Y_pred.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

lw = 2
plt.figure()
plt.plot(fpr["micro"], tpr["micro"],
  label='micro-average ROC curve (area = {0:0.2f})'
  ''.format(roc_auc["micro"]),
  color='deeppink', linestyle=':', linewidth=4)


colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])  # 几个类别就设置几个颜色
for i, color in zip(range(nb_classes), colors):
    plt.plot(fpr[i], tpr[i], color=color, lw=lw,
    label='ROC curve of class {0} (area = {1:0.2f})'
    ''.format(i, roc_auc[i]))

# plt.plot([0, 1], [0, 1], 'k--', lw=lw)    # 斜着的分界线
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.title('ROC曲线')
plt.legend(loc="lower right")
# plt.savefig("../images/ROC/ROC_3分类.png")
plt.show()

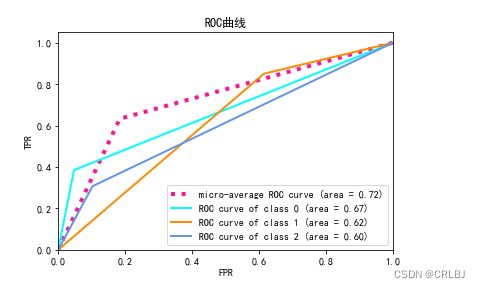
虚线为平均的ROC曲线，其余三条分别为0、1、2三类各自的ROC曲线。

混淆矩阵

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['font.family']='sans-serif'  # 解决绘图中文乱码
plt.rcParams['axes.unicode_minus'] = False   # 解决负号显示为框

# 混淆矩阵
classes = ['不录取','待考虑','录取']

confusion_matrix = model_LR.pred_table()

plt.figure(figsize=(6, 4), dpi=90)

plt.imshow(confusion_matrix, interpolation='nearest', cmap=plt.cm.Oranges)  #按照像素显示出矩阵
plt.title('混淆矩阵')
plt.colorbar()

tick_marks = np.arange(3)
plt.xticks(tick_marks, classes)
plt.yticks(tick_marks, classes, rotation=90,verticalalignment='center')

for x in range(len(confusion_matrix)):
    for y in range(len(confusion_matrix)):
        plt.annotate(confusion_matrix[y,x], xy = (x,y), horizontalalignment = 'center', verticalalignment = 'center')

plt.ylabel('Ground Truth')
plt.xlabel('Prediction')
plt.tight_layout()

（此例子的结果准确性确实比较差，主要是记录分享代码和流程，准确性还请忽略）

筛选协变量

根据AIC准则，使用前进后退法对协变量进行筛选，得到最优模型。（zhihu大佬的代码，亲测可用，我修改成了MNLogit，多加了几个输出结果）

#################################### 逐步回归（MNLogit）
def stepwise_select_MNLogit(data,label,cols_all,method='forward'):
    '''
    args:
        data：数据源，df
        label：标签，str
        cols_all：逐步回归的全部字段
        methrod：方法，forward:向前，backward:向后，both:双向
    return:
        select_col：最终保留的字段列表，list 
        summary：模型参数
        AIC：aic
    '''
    import statsmodels.api as sm
    
    ######################## 1.前向回归
    # 前向回归：从一个变量都没有开始，一个变量一个变量的加入到模型中，直至没有可以再加入的变量结束
    if method == 'forward':  
        add_col = [] 
        AIC_None_value = np.inf
        while cols_all:
            # 单个变量加入，计算aic
            AIC = {}
            for col in cols_all:
                print(col)
                X_col = add_col.copy()
                X_col.append(col)
                X = sm.add_constant(data[X_col])
                y = data[label]
                LR = sm.MNLogit(y, X).fit()
                AIC[col] = LR.aic
            AIC_min_value = min(AIC.values())   
            AIC_min_key = min(AIC,key=AIC.get)
            # 如果最小的aic小于不加该变量时的aic，则加入变量，否则停止
            if AIC_min_value < AIC_None_value:
                cols_all.remove(AIC_min_key)
                add_col.append(AIC_min_key)
                AIC_None_value = AIC_min_value
            else:
                break
        select_col = add_col
    ######################## 2.后向回归
    # 从全部变量都在模型中开始，一个变量一个变量的删除，直至没有可以再删除的变量结束
    elif method == 'backward': 
        p = True  
        # 全部变量，一个都不剔除，计算初始aic
        X_col = cols_all.copy()
        X = sm.add_constant(data[X_col])
        y = data[label]
        LR = sm.MNLogit(y, X).fit()
        AIC_None_value = LR.aic        
        while p:
            # 删除一个字段提取aic最小的字段
            AIC = {}
            for col in cols_all:
                print(col)
                X_col = [i for i in cols_all if i!=col]
                X = sm.add_constant(data[X_col])
                LR = sm.MNLogit(y, X).fit()
                AIC[col] = LR.aic
            AIC_min_value = min(AIC.values()) 
            AIC_min_key = min(AIC, key=AIC.get)  
            # 如果最小的aic小于不删除该变量时的aic，则删除该变量，否则停止
            if AIC_min_value < AIC_None_value:
                cols_all.remove(AIC_min_key)
                AIC_None_value = AIC_min_value
                p = True
            else:
                break 
        select_col = cols_all             
    ######################## 3.双向回归
    elif method == 'both': 
        p = True
        add_col = []
        # 全部变量，一个都不剔除，计算初始aic
        X_col = cols_all.copy()
        X = sm.add_constant(data[X_col])
        y = data[label]
        LR = sm.MNLogit(y, X).fit()
        AIC_None_value = LR.aic        
        while p: 
            # 删除一个字段提取aic最小的字段
            AIC={}
            for col in cols_all:
                print(col)
                X_col = [i for i in cols_all if i!=col]
                X = sm.add_constant(data[X_col])
                LR = sm.MNLogit(y, X).fit()
                AIC[col] = LR.aic     
            AIC_min_value = min(AIC.values())
            AIC_min_key = min(AIC, key=AIC.get)
            if len(add_col) == 0: # 第一次只有删除操作，不循环加入变量
                if AIC_min_value < AIC_None_value:
                    cols_all.remove(AIC_min_key)
                    add_col.append(AIC_min_key)
                    AIC_None_value = AIC_min_value
                    p = True
                else:
                    break
            else:
                # 单个变量加入，计算aic
                for col in add_col:
                    print(col)
                    X_col = cols_all.copy()
                    X_col.append(col)
                    X = sm.add_constant(data[X_col])
                    LR = sm.MNLogit(y, X).fit()
                    AIC[col] = LR.aic
                AIC_min_value = min(AIC.values())
                AIC_min_key = min(AIC, key=AIC.get)
                if AIC_min_value < AIC_None_value:
                    # 如果aic最小的字段在添加变量阶段产生，则加入该变量，如果aic最小的字段在删除阶段产生,则删除该变量
                    if AIC_min_key in add_col:
                        cols_all.append(AIC_min_key)
                        add_col = list(set(add_col)-set(AIC_min_key))
                        p = True                    
                    else: 
                        cols_all.remove(AIC_min_key)
                        add_col.append(AIC_min_key)
                        p = True
                    AIC_None_value = AIC_min_value
                else:
                    break
        select_col = cols_all 
    ######################## 模型
    X = sm.add_constant(data[select_col])
    LR = sm.MNLogit(y, X).fit()    
    summary = LR.summary()
    summary2 = LR.summary2()
    AIC = LR.aic
    return select_col,summary,summary2,AIC,LR

逐步回归

cols_all = X.drop(['intercept'],axis=1,inplace=False).columns
cols_all = list(cols_all)
cols ,summary ,summary2 ,AIC, model = stepwise_select_MNLogit(data,'admit',cols_all,method='both')

查看结果

summary2()

可以看到，age变量被剔除。（很合理，这列年龄是我自己使用随机数添加的，就是为了使用一下逐步回归法hhh）

部分代码实在不记得或找不到是从哪里偷师来的了，漏加引用实属抱歉。