周志华《机器学习》习题7.3——python实现朴素贝叶斯分类器

1.题目

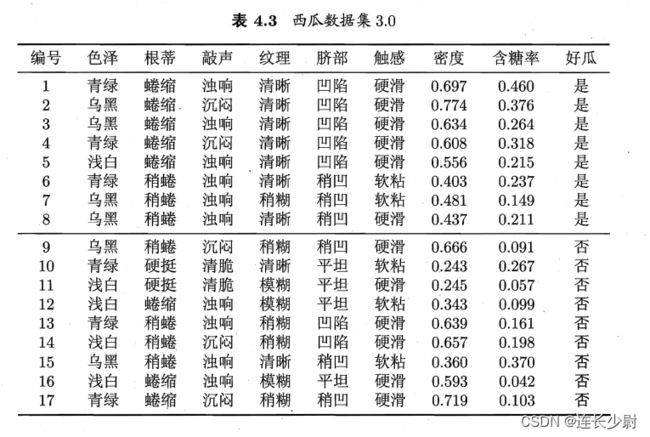
试编程实现拉普拉斯修正的朴素贝叶斯分类器，并以西瓜数据集3.0为训练集，对p151“测1”样本进行判别。

西瓜数据集3.0如下：

测1如下：

附文本版的西瓜数据集：

青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.460,是
乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是
乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是
青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是
浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是
青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是
乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是
乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是
乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否
青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否
浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否
浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否
青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否
浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否
乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.360,0.370,否
浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否
青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否

2. 思路+代码

第一步，实现数据集的获取，将训练数据放在x中，训练标签放在y中。

import numpy as np
import matplotlib.pyplot as plt
import math

def get_data():
    x = []
    y = []
    with open("./xigua.txt", 'r') as f:
        for line in f.readlines():
            words = line.split(',')
            x.append(words[:8])
            if '是' in words[8]:
                y.append(1)
            elif '否' in words[8]:
                y.append(0)
    return np.array(x), np.array(y)

然后，就可以开始实现学习器的训练过程了。首先在实现之前，我们需要明确，朴素贝叶斯分类器的预测过程用一个式子写出来就是：
$$h(\mathbf{x})=\underset{c\in y}{\mathrm{argmax}}P(c)\prod _d^{i=1}P(x_i|c)$$
其中 ，
h(x) 表示训练后的朴素贝叶斯分类器， x 表示样本或样本集，
argmax 下面的 c 表示类别， y 是全部类别，
P( c ) 表示对于每个类别的“先验概率”，在这里，朴素贝叶斯分类器会直接将训练集中每个类别所占的比例作为先验概率（例如，对于本题，P(c=好瓜) 就是 8/17）。用式子写出就是：
$$p(c)=\frac{\left|D_c\right|}{\left|D\right|}$$
$P(x_i|c)$ 是条件概率，表示给定一个类别，这个类别对应数据中第i个属性等于xi的概率（例如， P(x1=青绿|c=好瓜) 就表示一个好瓜的色泽是青绿的概率 ）。用式子写出就是：
$$P(x_i|c)=\frac{\left|D_{c,x_i}\right|}{\left|D_c\right|}$$
上述是属性为离散时的计算方法，而对于连续型属性，我们可以假定这个属性服从正太分布，然后通过训练数据估计得到mu和sigma（mu就是算均值，sigma^2就是算方差），这样就计算出了该属性得分布，然后将属性值带入到正太分布公式中，得到得概率结果就作为条件概率。

另外，有一种特殊情况，即某一个概率为0，这样在它们相乘的过程中，整体就为0，其他不为0的概率起不到作用，为了避免这种情况，需要进行拉普拉斯修正，其实很简单，就是在计算概率的过程中令每一项都加一，这样就可以避免条件概率为0，将修正后的P( c ) 和 $P(x_i|c)$ 为：
$$p(c)=\frac{\left|D_c\right|+1}{\left|D\right|+N}$$
$$p(c)=\frac{\left|D_{c,x_i}\right|+1}{\left|D_c\right|+N_i}$$
其中N表示可能出现的类别数，Ni表示第i个属性可能的取值数。

所以我们发现，训练过程实际上就是把上述的各种概率值都算出来，然后存储起来，当预测时，只需要把对应概率取出来，然后套到h(x)公式里就可以了。

明白了上述流程，就可以实现代码了：

def train_model():
    # 将分类器的概率值存储在model中
    model = {}
    train_data, train_lable = get_data()
    
    # 首先计算正反类的先验概率
    # model['pri_p_c1']为正类的先验概率，model['pri_p_c0']为反类的先验概率
    positive_cnt = np.sum(train_lable==1)
    negative_cnt = np.sum(train_lable==0)
    model['pri_p_c1'] = (positive_cnt + 1) / ((positive_cnt + negative_cnt) + 2)
    model['pri_p_c0'] = (negative_cnt + 1) / ((positive_cnt + negative_cnt) + 2)
    con_p_c1 = []
    con_p_c0 = []
    
    # 循环计算条件概率，
    # 第一层循环遍历每个属性（不包括连续属性），i表示每种属性
    for i in range(len(train_data[0])-2):
        # cnt_in_c1和cnt_in_c0存储，正、反类中，属性i的每种取值对应样例数量
        # 例： cnt_in_c1['青绿'] 表示“好瓜中色泽为青绿的有几个瓜”
        cnt_in_c1 = dict()
        cnt_in_c0 = dict()
        
        # 第二层循环遍历所有训练数据，j表示每条训练数据
        for j in range(len(train_data)):
            if not train_data[j][i] in cnt_in_c1.keys():
                cnt_in_c1[train_data[j][i]] = 0
            if not train_data[j][i] in cnt_in_c0.keys():
                cnt_in_c0[train_data[j][i]] = 0
                
            if train_lable[j] == 1:
                cnt_in_c1[train_data[j][i]] += 1
            elif train_lable[j] == 0:
                cnt_in_c0[train_data[j][i]] += 1
        
        # p_xi_given_c1表示条件概率
        # 例：p_xi_given_c1['青绿'] 表示“好瓜色泽为青绿的概率”
        p_xi_given_c1 = {}
        for key in cnt_in_c1.keys():
            # 拉普拉斯修正要求分子+1，分母+n
            p_xi_given_c1[key] = (cnt_in_c1[key] + 1) / (positive_cnt + len(cnt_in_c1))
        con_p_c1.append(p_xi_given_c1)
        
        p_xi_given_c0 = {}
        for key in cnt_in_c0.keys():
            p_xi_given_c0[key] = (cnt_in_c0[key] + 1) / (negative_cnt + len(cnt_in_c0))
        con_p_c0.append(p_xi_given_c0) 
     
    # 遍历每个连续属性，i表示每种属性
    for i in range(len(train_data[0])-2, len(train_data[0])):
        p_xi_given_c1 = dict()
        p_xi_given_c0 = dict()
        p_xi_given_c1['mu'] = 0
        p_xi_given_c1['sigma'] = 0
        p_xi_given_c0['mu'] = 0
        p_xi_given_c0['sigma'] = 0
        
        # 计算均值
        for j in range(len(train_data)):
            if train_lable[j] == 1:
                p_xi_given_c1['mu'] += float(train_data[j][i])
            elif train_lable[j] == 0:
                p_xi_given_c0['mu'] += float(train_data[j][i])
        p_xi_given_c1['mu'] = p_xi_given_c1['mu'] / positive_cnt
        p_xi_given_c0['mu'] = p_xi_given_c0['mu'] / negative_cnt
        
        # 计算方差
        for j in range(len(train_data)):
            if train_lable[j] == 1:
                p_xi_given_c1['sigma'] += (float(train_data[j][i]) - p_xi_given_c1['mu'])**2
            elif train_lable[j] == 0:
                p_xi_given_c0['sigma'] += (float(train_data[j][i]) - p_xi_given_c0['mu'])**2
        p_xi_given_c1['sigma'] =  np.sqrt(p_xi_given_c1['sigma'] / positive_cnt)
        p_xi_given_c0['sigma'] = np.sqrt(p_xi_given_c0['sigma'] / negative_cnt)
        
        con_p_c1.append(p_xi_given_c1)
        con_p_c0.append(p_xi_given_c0)
    
    model['con_p_c1'] = con_p_c1
    model['con_p_c0'] = con_p_c0
    
    return model

正态分布函数：

# 正态分布公式
def N(mu, sigma, x):
    return np.exp(-(x-mu)**2/(2*sigma**2)) / (np.sqrt(2*np.pi) * sigma)

然后就可以预测了，预测过程很简单，就是按照h(x)那个公式，从model中取出需要得概率，然后算一下取最大对应类别就可以了。

def predict(model, x):
    p_c1 = model['pri_p_c1']
    p_c0 = model['pri_p_c0']
    for i in range(len(x)-2):
        p_c1 *= model['con_p_c1'][i][x[i]]
        p_c0 *= model['con_p_c0'][i][x[i]]
    for i in range(len(x)-2, len(x)):
        p_c1 *= N(model['con_p_c1'][i]['mu'], model['con_p_c1'][i]['sigma'], float(x[i]))
        p_c0 *= N(model['con_p_c0'][i]['mu'], model['con_p_c0'][i]['sigma'], float(x[i]))
    print("p_c0:", p_c0, "\np_c1", p_c1)
    return np.argmax([p_c0, p_c1])

然后，开始训练，并打印一下训练得到得概率值：

model = train_model() 
for key in model.keys():
    print(key, ":\n", model.get(key))

其中：
pri_p_c1: 正类的先验概率
pri_p_c0 : 反类的先验概率
con_p_c1 : 正类的条件概率
con_p_c0 : 反类的条件概率
将书中“测1”代入模型进行预测：

text_x1 = ['青绿','蜷缩','浊响','清晰','凹陷','硬滑','0.697','0.460']
y = predict(model, text_x1)
if y == 1:
    print("好瓜")
else:
    print("坏瓜")

结果如下：

可以看到预测结果正确，
另外，因为书中p152结果是不加修正的结果，所以和书上的有所偏差，要比不加修正的结果值要小。