Cosine decay with warmup和 周期性学习率(CLR)(学习率更新方式)
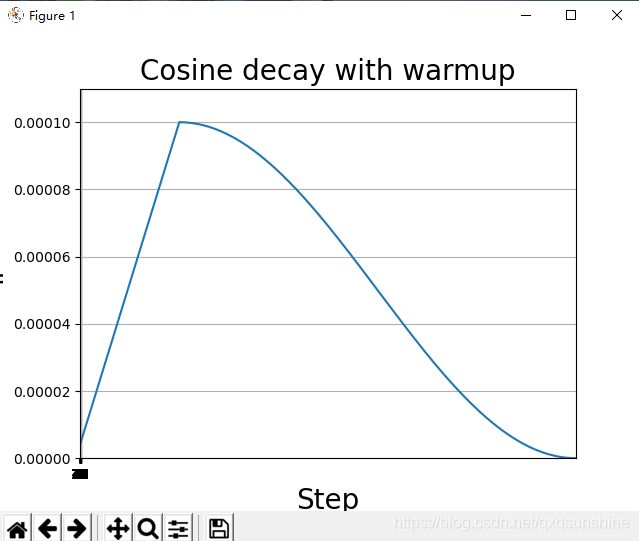
Cosine decay with warmup:
import numpy as np
from tensorflow import keras
from keras import backend as K
# 带有warm-up的cosine学习率
def cosine_decay_with_warmup(global_step,
learning_rate_base,
total_steps,
warmup_learning_rate=0.0,
warmup_steps=0,
hold_base_rate_steps=0):
"""Cosine decay schedule with warm up period.
Cosine annealing learning rate as described in:
Loshchilov and Hutter, SGDR: Stochastic Gradient Descent with Warm Restarts.
ICLR 2017. https://arxiv.org/abs/1608.03983
In this schedule, the learning rate grows linearly from warmup_learning_rate
to learning_rate_base for warmup_steps, then transitions to a cosine decay
schedule.
Arguments:
global_step {int} -- global step.
learning_rate_base {float} -- base learning rate.
total_steps {int} -- total number of training steps.
Keyword Arguments:
warmup_learning_rate {float} -- initial learning rate for warm up. (default: {0.0})
warmup_steps {int} -- number of warmup steps. (default: {0})
hold_base_rate_steps {int} -- Optional number of steps to hold base learning rate
before decaying. (default: {0})
Returns:
a float representing learning rate.
Raises:
ValueError: if warmup_learning_rate is larger than learning_rate_base,
or if warmup_steps is larger than total_steps.
"""
if total_steps < warmup_steps:
raise ValueError('total_steps must be larger or equal to '
'warmup_steps.')
learning_rate = 0.5 * learning_rate_base * (1 + np.cos(
np.pi *
(global_step - warmup_steps - hold_base_rate_steps
) / float(total_steps - warmup_steps - hold_base_rate_steps)))
if hold_base_rate_steps > 0:
learning_rate = np.where(global_step > warmup_steps + hold_base_rate_steps,
learning_rate, learning_rate_base)
if warmup_steps > 0:
if learning_rate_base < warmup_learning_rate:
raise ValueError('learning_rate_base must be larger or equal to '
'warmup_learning_rate.')
slope = (learning_rate_base - warmup_learning_rate) / warmup_steps
warmup_rate = slope * global_step + warmup_learning_rate
learning_rate = np.where(global_step < warmup_steps, warmup_rate,
learning_rate)
return np.where(global_step > total_steps, 0.0, learning_rate)
class WarmUpCosineDecayScheduler(keras.callbacks.Callback):
"""Cosine decay with warmup learning rate scheduler
"""
def __init__(self,
learning_rate_base,
total_steps,
global_step_init=0,
warmup_learning_rate=0.0,
warmup_steps=0,
hold_base_rate_steps=0,
verbose=0):
"""Constructor for cosine decay with warmup learning rate scheduler.
Arguments:
learning_rate_base {float} -- base learning rate.
total_steps {int} -- total number of training steps.
Keyword Arguments:
global_step_init {int} -- initial global step, e.g. from previous checkpoint.
warmup_learning_rate {float} -- initial learning rate for warm up. (default: {0.0})
warmup_steps {int} -- number of warmup steps. (default: {0})
hold_base_rate_steps {int} -- Optional number of steps to hold base learning rate
before decaying. (default: {0})
verbose {int} -- 0: quiet, 1: update messages. (default: {0})
"""
super(WarmUpCosineDecayScheduler, self).__init__()
self.learning_rate_base = learning_rate_base
self.total_steps = total_steps
self.global_step = global_step_init
self.warmup_learning_rate = warmup_learning_rate
self.warmup_steps = warmup_steps
self.hold_base_rate_steps = hold_base_rate_steps
self.verbose = verbose
self.learning_rates = []
def on_batch_end(self, batch, logs=None):
self.global_step = self.global_step + 1
lr = K.get_value(self.model.optimizer.lr)
self.learning_rates.append(lr)
def on_batch_begin(self, batch, logs=None):
lr = cosine_decay_with_warmup(global_step=self.global_step,
learning_rate_base=self.learning_rate_base,
total_steps=self.total_steps,
warmup_learning_rate=self.warmup_learning_rate,
warmup_steps=self.warmup_steps,
hold_base_rate_steps=self.hold_base_rate_steps)
K.set_value(self.model.optimizer.lr, lr)
if self.verbose > 0:
print('\nBatch %05d: setting learning '
'rate to %s.' % (self.global_step + 1, lr))
if __name__ == '__main__':
from keras.models import Sequential
from keras.layers import Dense
# Create a model.
model = Sequential()
model.add(Dense(32, activation='relu', input_dim=100))
model.add(Dense(10, activation='softmax'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
# Number of training samples.
# gen1
sample_count = 12608
# gen
# Total epochs to train.
epochs = 50
# Number of warmup epochs.
warmup_epoch = 10
# Training batch size, set small value here for demonstration purpose.
batch_size = 16
# Base learning rate after warmup.
learning_rate_base = 0.0001
total_steps = int(epochs * sample_count / batch_size)
# Compute the number of warmup batches.
warmup_steps = int(warmup_epoch * sample_count / batch_size)
# Generate dummy data.
data = np.random.random((sample_count, 100))
labels = np.random.randint(10, size=(sample_count, 1))
# Convert labels to categorical one-hot encoding.
one_hot_labels = keras.utils.to_categorical(labels, num_classes=10)
# Compute the number of warmup batches.
warmup_batches = warmup_epoch * sample_count / batch_size
# Create the Learning rate scheduler.
warm_up_lr = WarmUpCosineDecayScheduler(learning_rate_base=learning_rate_base,
total_steps=total_steps,
warmup_learning_rate=4e-06,
warmup_steps=warmup_steps,
hold_base_rate_steps=5,
)
# Train the model, iterating on the data in batches of 32 samples
model.fit(data, one_hot_labels, epochs=epochs, batch_size=batch_size,
verbose=0, callbacks=[warm_up_lr])
import matplotlib.pyplot as plt
plt.plot(warm_up_lr.learning_rates)
plt.xlabel('Step', fontsize=20)
plt.ylabel('lr', fontsize=20)
plt.axis([0, total_steps, 0, learning_rate_base * 1.1])
plt.xticks(np.arange(0, epochs, 1))
plt.grid()
plt.title('Cosine decay with warmup', fontsize=20)
plt.show()效果:
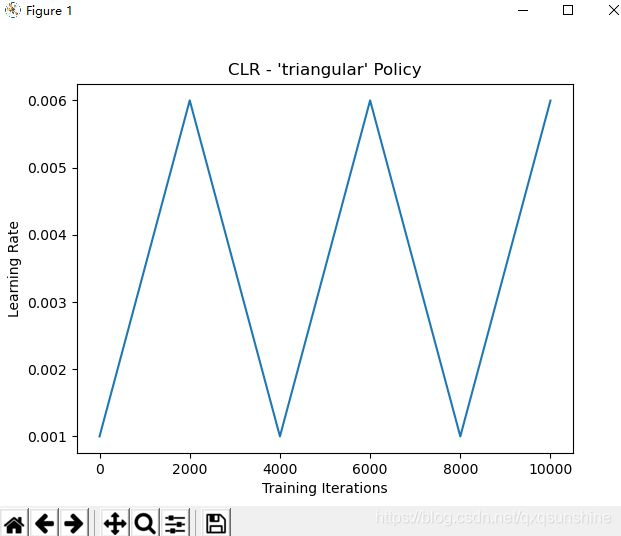
周期性学习率(CLR):
from keras.callbacks import *
from keras.models import Sequential, Model
from keras.layers import Dense, Activation, Input
from keras.optimizers import *
import matplotlib.pyplot as plt
'''循环学习率是学习率调整的策略,其在周期性质中将学习率从基值增加。
通常,周期的频率是恒定的,但是振幅通常在每个周期或每个小批量迭代中动态地缩放。
'''
class CyclicLR(Callback):
"""This callback implements a cyclical learning rate policy (CLR).
The method cycles the learning rate between two boundaries with
some constant frequency, as detailed in this paper (https://arxiv.org/abs/1506.01186).
The amplitude of the cycle can be scaled on a per-iteration or
per-cycle basis.
This class has three built-in policies, as put forth in the paper.
"triangular":
A basic triangular cycle w/ no amplitude scaling.
"triangular2":
A basic triangular cycle that scales initial amplitude by half each cycle.
"exp_range":
A cycle that scales initial amplitude by gamma**(cycle iterations) at each
cycle iteration.
For more detail, please see paper.
# Example
```python
clr = CyclicLR(base_lr=0.001, max_lr=0.006,
step_size=2000., mode='triangular')
model.fit(X_train, Y_train, callbacks=[clr])
```
Class also supports custom scaling functions:
```python
clr_fn = lambda x: 0.5*(1+np.sin(x*np.pi/2.))
clr = CyclicLR(base_lr=0.001, max_lr=0.006,
step_size=2000., scale_fn=clr_fn,
scale_mode='cycle')
model.fit(X_train, Y_train, callbacks=[clr])
```
# Arguments
base_lr: initial learning rate which is the
lower boundary in the cycle.
max_lr: upper boundary in the cycle. Functionally,
it defines the cycle amplitude (max_lr - base_lr).
The lr at any cycle is the sum of base_lr
and some scaling of the amplitude; therefore
max_lr may not actually be reached depending on
scaling function.
step_size: number of training iterations per
half cycle. Authors suggest setting step_size
2-8 x training iterations in epoch.
mode: one of {triangular, triangular2, exp_range}.
Default 'triangular'.
Values correspond to policies detailed above.
If scale_fn is not None, this argument is ignored.
gamma: constant in 'exp_range' scaling function:
gamma**(cycle iterations)
scale_fn: Custom scaling policy defined by a single
argument lambda function, where
0 <= scale_fn(x) <= 1 for all x >= 0.
mode paramater is ignored
scale_mode: {'cycle', 'iterations'}.
Defines whether scale_fn is evaluated on
cycle number or cycle iterations (training
iterations since start of cycle). Default is 'cycle'.
"""
def __init__(self, base_lr=0.001, max_lr=0.006, step_size=2000., mode='triangular',
gamma=1., scale_fn=None, scale_mode='cycle'):
super(CyclicLR, self).__init__()
self.base_lr = base_lr
self.max_lr = max_lr
self.step_size = step_size
self.mode = mode
self.gamma = gamma
if scale_fn == None:
if self.mode == 'triangular':
self.scale_fn = lambda x: 1.
self.scale_mode = 'cycle'
elif self.mode == 'triangular2':
self.scale_fn = lambda x: 1 / (2. ** (x - 1))
self.scale_mode = 'cycle'
elif self.mode == 'exp_range':
self.scale_fn = lambda x: gamma ** (x)
self.scale_mode = 'iterations'
else:
self.scale_fn = scale_fn
self.scale_mode = scale_mode
self.clr_iterations = 0.
self.trn_iterations = 0.
self.history = {}
self._reset()
def _reset(self, new_base_lr=None, new_max_lr=None,
new_step_size=None):
"""Resets cycle iterations.
Optional boundary/step size adjustment.
"""
if new_base_lr != None:
self.base_lr = new_base_lr
if new_max_lr != None:
self.max_lr = new_max_lr
if new_step_size != None:
self.step_size = new_step_size
self.clr_iterations = 0.
def clr(self):
cycle = np.floor(1 + self.clr_iterations / (2 * self.step_size))
x = np.abs(self.clr_iterations / self.step_size - 2 * cycle + 1)
if self.scale_mode == 'cycle':
return self.base_lr + (self.max_lr - self.base_lr) * np.maximum(0, (1 - x)) * self.scale_fn(cycle)
else:
return self.base_lr + (self.max_lr - self.base_lr) * np.maximum(0, (1 - x)) * self.scale_fn(
self.clr_iterations)
def on_train_begin(self, logs={}):
logs = logs or {}
if self.clr_iterations == 0:
K.set_value(self.model.optimizer.lr, self.base_lr)
else:
K.set_value(self.model.optimizer.lr, self.clr())
def on_batch_end(self, epoch, logs=None):
logs = logs or {}
self.trn_iterations += 1
self.clr_iterations += 1
self.history.setdefault('lr', []).append(K.get_value(self.model.optimizer.lr))
self.history.setdefault('iterations', []).append(self.trn_iterations)
for k, v in logs.items():
self.history.setdefault(k, []).append(v)
K.set_value(self.model.optimizer.lr, self.clr())
if __name__ == '__main__':
'''
一个epoch是至将整个训练集训练一轮。如果我们令batch_size等于100(每次使用100个样本进行训练),
那么一个epoch总共需要计算500次iteration。
iteration : 一代中进行了多少次迭代 np.ceil(train_data / batch_size)
'''
inp = Input(shape=(15,))
x = Dense(10, activation='relu')(inp)
x = Dense(1, activation='sigmoid')(x)
model = Model(inp, x)
X = np.random.rand(2000000, 15)
Y = np.random.randint(0, 2, size=2000000)
clr_triangular = CyclicLR(mode='triangular')
model.compile(optimizer=SGD(0.1), loss='binary_crossentropy', metrics=['accuracy'])
model.fit(X, Y, batch_size=2000, nb_epoch=10, callbacks=[clr_triangular], verbose=0)
plt.figure()
plt.plot(clr_triangular.history['iterations'], clr_triangular.history['lr'])
plt.xlabel('Training Iterations')
plt.ylabel('Learning Rate')
plt.title("CLR - 'triangular' Policy")
plt.show()
# clr_triangular = CyclicLR(mode='triangular2')
# model.compile(optimizer=SGD(), loss='binary_crossentropy', metrics=['accuracy'])
# model.fit(X, Y, batch_size=2000, nb_epoch=20, callbacks=[clr_triangular], verbose=0)
# clr_triangular._reset()
# model.fit(X, Y, batch_size=2000, nb_epoch=10, callbacks=[clr_triangular], verbose=0)
# plt.xlabel('Training Iterations')
# plt.ylabel('Learning Rate')
# plt.title("'triangular2' Policy Reset at 20000 Iterations")
# plt.plot(clr_triangular.history['iterations'], clr_triangular.history['lr'])
(来自于博客:https://blog.csdn.net/qq_38410428/article/details/88061738,里面还有其他的可以用的,写的非常好)
这个类的参数包括:
base_lr:初始学习率,这是周期中的下限。这会覆盖优化器lr。默认值为0.001。
max_lr:循环中的上边界。在功能上,它定义了循环幅度(max_lr- base_lr)。任何周期的lr是base_lr幅度的总和和一些比例; 因此,max_lr根据缩放功能,实际上可能无法达到。默认0.006。
step_size:每半个周期的训练迭代次数。作者建议设定step_size = (2-8) x (training iterations in epoch)。默认2000。
mode:其中一个{‘triangular’, ‘triangular2’, ‘exp_range’}。值对应于下面详述的策略。如果scale_fn不是None,则忽略该参数。默认’triangular’。
gamma:‘exp_range’缩放功能常数,gamma^(cycle iterations)。默认1。
scale_fn:自定义扩展策略由单个参数lambda函数定义,0 <= scale_fn(x) <= 1适用于所有x >= 0。mode使用此参数时,将忽略该参数。默认None。
scale_mode:{‘cycle’, ‘iterations’}。定义是否scale_fn根据循环次数或循环迭代进行评估(自循环开始后的训练迭代)。默认是’cycle’。