本文基于台大机器学习技法系列课程进行的笔记总结。
一、主要内容
topic 1 深度神经网络结构
从类神经网络结构中我们已经发现了神经网络中的每一层实际上都是对前一层进行的特征转换,也就是特征抽取。
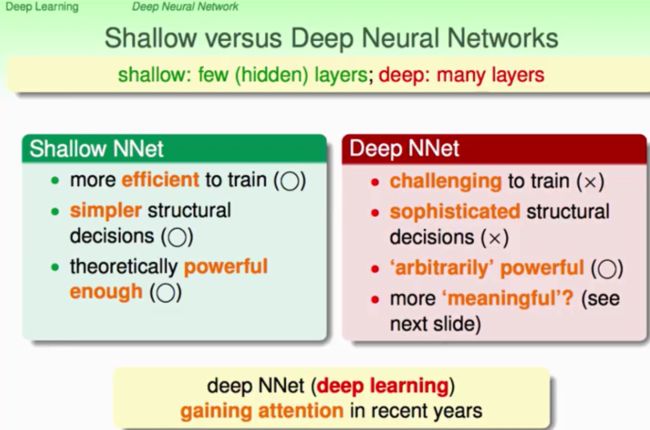
一般的隐藏层(hidden layer)较少的类神经网络结构我们称之为shallow,而当隐藏层数比較多的类神经网络结构我们称之为deep。例如以下图所看到的:
从两者的对照中能够明显发现,随着类神经网络结构的层数逐渐变多,由shallow转向deep,训练的效率会下降,结构变得复杂。那么相应的能力(powerful)呢?实际上shallow的类神经网络已经非常强的powerful了。那么多添加layer的目的究竟是什么呢?是怎样的更加富有意义(meaningful)呢?且往下看:
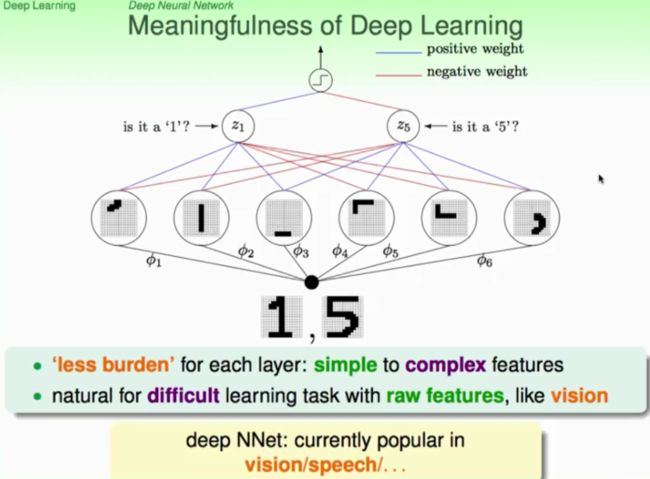
图中所看到的的一个很常见的问题:识别手写体数字的模式识别问题。最原始的特征就是我们的原始数字化的图像(raw features:pixels)。从pixels出发。通过第一层的转换我们能够得到一些略微复杂一点点的features:笔画特征,然后我们再由这些笔画特征開始输入到下一层中,就能够得到更加抽象的认识特征(将像素组合成笔画,然后再由笔画的组成去构成对数字的认识,进而识别数字)。上图中能够看出。数字1能够由第一层的左边三个笔画构成,而数字5能够由第一层右边四个笔画构成,从第一层到第二层,链接权重红色表示抑制,蓝色表示激励。事实上就是模仿人类神经元的工作机制(最简单的模仿:激励和抑制)。那么这个手写体数字的模式识别问题就能够通过这一层一层的类神经网络结构得到解决。可是问题是。类神经网络的结构怎样确定,模型复杂度怎样评估(会不会overfitting呢),以及优化的方式和计算复杂度的评估呢?且看下图总结:
对于第一个问题,怎样确定类神经网络的结构。能够通过domain knowledge来解决,比方在图像处理中应用的卷积神经网络,就是利用了像素在空间上的关系。
对于第二个问题,我们知道一个很经典的关系,overfitting与模型复杂度、数据量、噪声的关系:模型复杂度越大,数据量越小,噪声越大,就越easy发生overfitting,反之亦然。所以,假设我们训练时候的数据量足够大,就全然能够消弭因为模型复杂度带来的overfitting的风险。所以,对于模型复杂度。要保证足够大的数据量。当然,第二种我们最熟悉的用来抑制模型复杂度的工具就是regularization,通过对噪声的容忍(noise-tolerant)对象不同能够有两种regularization的方式:对网络节点退化能够容忍的dropout以及对输入数据退化能够容忍的denoising。都表如今对噪声的抑制。所以,第二个问题能够通过在数据量上的保证和对噪声的抑制来解决。
对于第三个问题。deep learning的layer越多。权重也就越多,在进行优化的时候就更加easy出现局部最优,由于变量多了,想象一下。似乎连绵起伏的山一样,局部最优的情况也就更加easy发生。那么假设克服发生局部最优的优化问题呢?
能够通过一个叫做pre-training的方法。谨慎的对权重进行初始化。使得权重一開始就出如今全局最优的那个“山峰”上,然后通过梯度下降或者随机梯度的方式往下滚,直到全局最优。所以。这个pre-training就能够克服局部最优的问题。后面也将是我们解说的一个重点。
对于第四个问题。计算的复杂度是与deep learning的结构复杂度正相关的。可是不用操心,一个强有力的硬件支持或者架构支持已经被用来进行深度神经网络的训练和计算,那就是GPU或FPGA这样的能够进行大量的硬件上的并行计算的处理器。
所以第四个问题仅仅要通过选择专用的硬件平台就能够解决。
那么四个问题都加以了分析和解决。我们以下的重点在于pre-training的机制,怎样获得较好的网络初始值呢?
上图就是典型的深度神经网络的训练过程,先通过pre-training进行网络參数的初始设置。然后再通过第二步利用误差回传机制对网络參数进行调优(fine-tune)。
那么这个pre-training的详细是怎样进行的呢?实际上就是如上图所看到的,每次仅仅进行两层之间的參数训练。确定之后再往其紧接着的上面两层參数进行训练。就这样逐层的训练。那么训练的机制呢?就是今天的第二个topic。autoencoder,自己主动编码器。
topic 2 自己主动编码器
那么我们看。自己主动编码器是怎样实现的。在这之前。先说明一个概念:information preserving,就是信息保持,我们在层与层之间的进行的特征转换实际上就是一个编码的过程。那么一个好的编码就是可以做到information preserving。
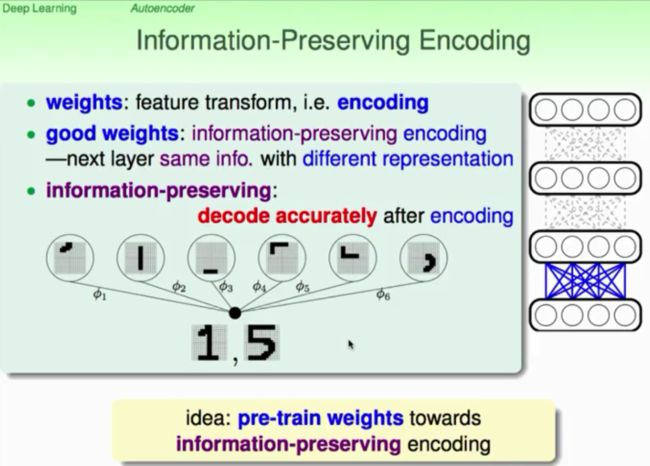
所以一个好的特征转换就是转换后的特征可以最大限度地保留原始信息。而不至于使得信息变得面目全非。转换后的特征是raw features的一个好的representation。且看下图:
我们还以原来的手写体数字的识别为例。将原始特征(raw features,pixels)转换为笔画特征是一个好的特征转换吗?能够保持原始信息吗?那么怎样衡量这个信息是不是丢失了呢?自然而然就想到了。我把数字1的转化成了笔画,那么这些笔画能不能又一次组合表示为数字1呢?依据上面的介绍。我们能够做到从1到笔画。然后还能够从笔画再到1的过程。这就是非常好的信息保持(information preserving)。
那么依据这样的由输入通过一层hidden layer,然后再转变为输入的机制去评估信息保持的效果,去衡量特征转化的品质。那么就得到下面的一个训练机制,且看下图:
这就是我们要将的pre-training的机制。
由输入经编码权重得到原始数据的特征转换,然后再由特征转换经解码权重得到原始数据的机制。
整个映射实际上就是一个identity function。由于输出=输入嘛!
那么实际上我们设计的这个训练过程能够应用到监督学习和非监督学习。对于监督学习,我们能够用来学习数据的informative representation,hidden layer的输出就是。
对于非监督学习,我们能够用来进行密度预计(density estimation):当g(x)≈x时的x处的密度更大;还能够用来进行outlier检測:那些g(x)与x相差远的x就能够作为outlier。那些g(x)≈x的隐藏层输出。能够作为x的典型表示(typical representation)。
因此,一个主要的autoencoder的完整流程就有了,且看下图:
由于上面解释的就比較多了,以下就不再对这个流程进行具体说明。一个须要点出的就是使得编码权重Wij与解码权重Wji相等能够用来作为一种形式的regularization。
而整个训练一层一层的进行实际上就是一个仅仅有两层的类神经网络。进行误差回传和梯度下降计算的复杂度都不会非常大。
有了pre-training。于是乎我们的deep learning的过程就变成了下图:
上面讲完了通过pre-training得到较好的初始权重。以便于整个deep learning可以在開始训练的时候就站在一个很好的位置,即在一定程度上避免因为模型结构复杂度导致的overfitting发生的风险。
由此引出的autoencoder。
那么前面讲为了克服overfitting的风险。还能够从还有一个角度:noise的角度出发。以下我们就进行denoising autoencoder的相关内容。
topic 3 去噪自己主动编码器
在类神经网络中事实上已经介绍过一些用于regularization的方法,比方通过限制模型输出的精度、权重的消减或者提前终止训练等,那么以下介绍的是一种比較另类的regularization的方法。
上面说了,基于消除噪声的方式。一般直接的想法或者经常使用的是data cleaning/pruning,那么我们这里介绍的也不是这样的常规的方法,而是一种反向思维的方式:假设我直接往输入数据中增加人工的噪声呢?会发生什么样的情况。这就是我们以下要探讨的去噪自己主动编码器。
这种往input中加入噪声的思维是以robustness健壮性出发的,试想假设我加完噪声后的数据作为输入,经过编码和解码后,假设输出依旧等于加入噪声前的数据。这种类神经网络结构是不是非常的稳健,也就说抗干扰能力非常强。
基于此想法。我们就得到denoising autoencoder的方法。且看下图
所以输入时x+人工噪声,标签是x。这样来对网络进行训练,这种神经网络结构自然就具备了denosing的效果。
topic 4 线性自己主动编码器与主成分分析
所曾经面讲的都是直接基于非线性映射的结构。而一般上我们经常是先通过线性的解释,然后再拓展至非线性。
那么我们看看线性自己主动编码器是如何的,看下图:
我们依旧通过平方误差进行推导。推导过程见下图。总之就是一堆矩阵的运算。假设学过矩阵分析课程看起来并不复杂,实际上就是进行谱分解。看不懂也没关系,仅仅要知道处理过程就好,求输入矩阵的最大特征值和其相应的特征向量,实际上这也是PCA处理的过程(PCA基于matlab的代码链接,小弟资源分不够。求个资源分勿怪)。
那么实际上,linear 的autoencoder实际上与主成分分析是很相近的。仅仅只是主成分分析具有统计学的说明。进行特征转换后的方差要大。
我们把数据进行零均值化作为autoencoder的输入,结果就跟PCA一样了。详细的关系能够看下图说明:
*************************************************************************************************************************************
通过以上的介绍。相信对整个deep learning的架构有了一定认识。当然这里面介绍的大部分都是入门级的知识,只是有了一个guideline之后,再去对更加细节的设计方法进行学习时就能有更加宏观方向的把握。