多径信道仿真参数
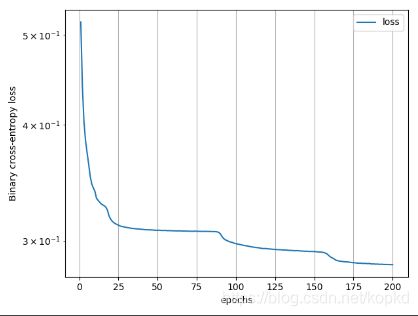
训练参数:
在神经网络中
训练信噪比 :12 dB
训练次数 : 200epoch
多径信道相关参数(一)fd = 56hz:
载波频率 fc = 2010MHZ
多普勒效应 车辆速度 V = 30KM/h
光速 c = 1.08*10^(9)KM/h
最大多普勒频移 fd = (v*fc)/c = 56hz
入射波数目 N = 20 (理解是这个与速度v有关,通过对比,入射波数目为40 ,这里推测为 20)
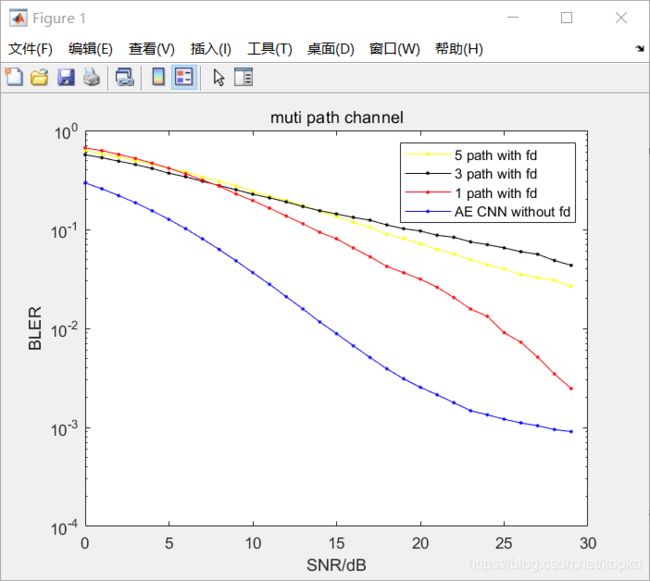
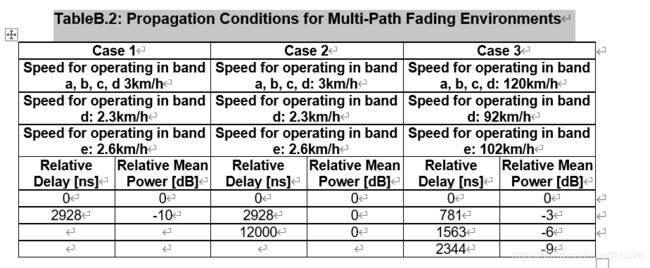
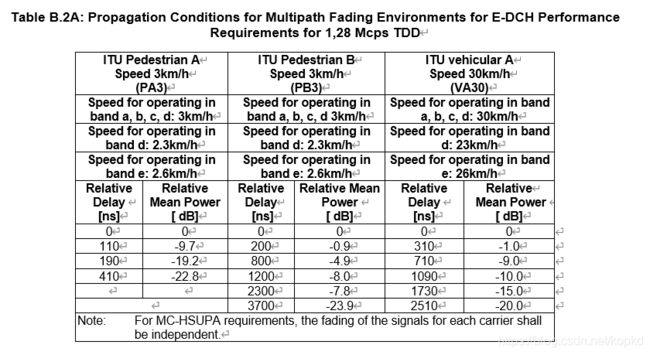
下图种多径参数以及其所适应的环境

python AE fd-56 仿真 5径训练
python AE fd-56 仿真 5径测试
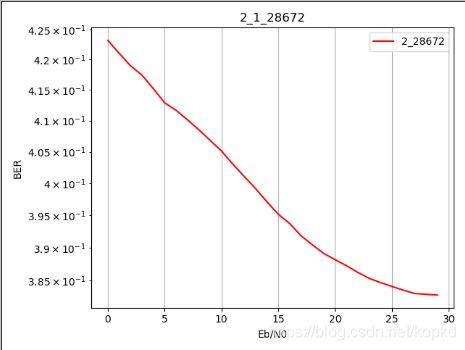
python AE fd-56 仿真 3径训练
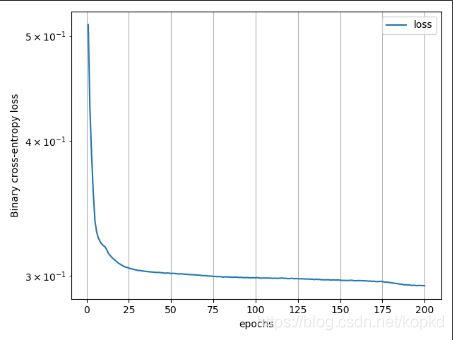
python AE fd-56 仿真 3径测试

python AE fd-56 仿真 1径训练

python AE fd-56 仿真 1径测试
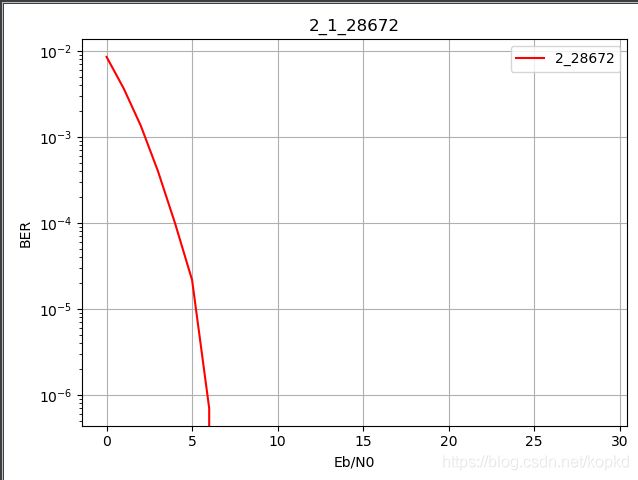
换算成延时点数和相对功率增益如下:
相对延时(单位:点数):
0 10 22 33 54 77
计算公式如下:
参考资料:
《LTE相关标准》首先确定子载波间隔为15000Hz,所以OFDM符号的长度是1/15000秒,再确定FFT点数为2048,所以采样间隔=时间/点数=1/15000/2048=1/(15000*2048)=1/30.72M直接从采样时间间隔来说明。
sr = 15000 # 一秒钟传多少个OFDM符号
Ns = 2048 # 一个OFDM符号所包含的符号
ts = 1/sr/Ns # 采样间隔
用延时/ts 就可以得到延时点数
相对功率增益:
sqrt(1/2) sqrt(2/5) sqrt(3/50) sqrt(1/20) sqrt(2/125) sqrt (1/200)
公式计算 :
power= 10.^(powerdB / 10); #信道抽头功率分布(线性)
sqrt(power / 2)
===================================================
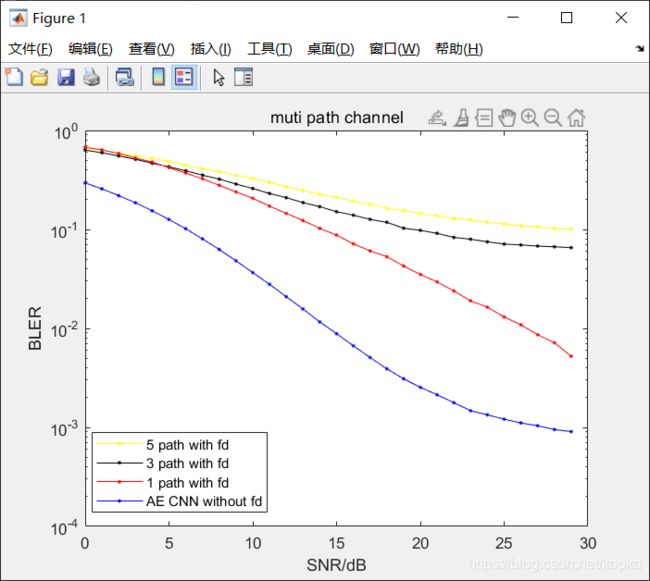
下面是matlab中仿真的效果(碰到的问题是这套参数中的仿真,3径效果没有5径的好):
延时点数(从左到右分别是1径到5径) 0 10 22 33 54 (自动编解码)
延时点数(从左到右分别是1径到5径) 0 6 14 22 33 (matlab)
这里自动编解码中延时和matlab中延时点数不同的原因是因为两者数据得格式是不同的,自动编解码中数据得结构是142048 matlab中数据的结构式是780。就导致两者的采样间隔式不同的,需要分开计算
多径信道相关参数(二)fd = 223:
载波频率 fc = 2017MHZ (传输的带宽)
多普勒效应 速度 V = 120KM/h
光速 c = 1.08*10^(9)
最大多普勒频移 fd = (v*fc)/c = 223hz
入射波数目 N = 80(理解是这个与速度v有关,之前代码种120KM/h时,入射波数目为40 ,这里推测为40)
相对功率增益:
sqrt(1/2) sqrt(1/4) sqrt(1/8) sqrt(1/16) sqrt(3/100)
相对延时(单位:点数):
0 16 31 47 63 这是在一个OFDM符号里面包含80个符号的情况下测得延时点数(matlab中)
0 26 52 78 103 这是在一个OFDM符号里面包含2048+160个符号的情况下测得延时点数(自动编解码神经网络)。 (一秒钟传15000*2048个符号)
0 24 48 72 96这是在一个OFDM符号里面包含2048个符号的情况下测得延时点数(自动编解码神经网络)。 (一秒钟传15000*2048个符号)
用comm.RayleighChannel()来生成多径信道
python端
训练 200 epoch
卷积核个数 8 个 3x3
训练信噪比 12dB
3径训练

1径训练
1径训测试
多径信道相关参数(三 )fd =100–matlab参数:
matlab端:
fd = 100
主要参数如下:

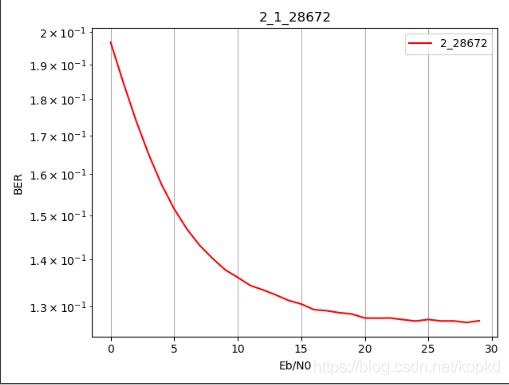
仿真结果:

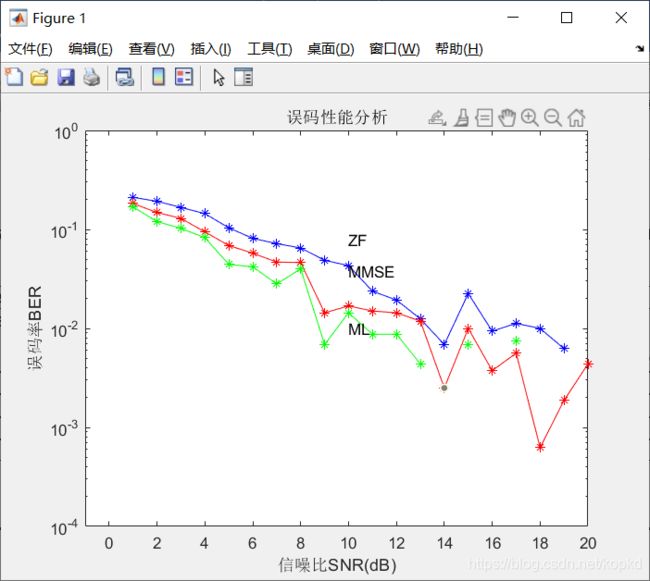
QPSK一径瑞利信道在三种均衡方式时的误码率
16QAM一径瑞利信道在三种均衡方式时的误码率
cost207典型城区(TU)信道参数
在这里插入图片描述
功率增益
powerdB = [0 -3 -6 -9 -12]; % 信道抽头功率分布(dB)
power = 10.^(powerdB / 10); % 信道抽头功率分布(线性)
ntap = length(powerdB); % 信道抽头数
channel = (randn(1, ntap) + 1i * randn(1, ntap)).* sqrt(power / 2);
时间延时
delay = [0 24 48 72 96]; % 信道延迟样本
lch = delay(end)+1; % 信道长度 信道脉冲响应 (这里为什么加1原因
% 也很简单 因为第一径没有延时,也就是0延时
% 相应对应的就是第一个位置,所以,0延时=>>位置1)
h = zeros(1, lch);
h(delay + 1) = channel; % 这里信道的长度是97,其中有数据的地方分别是
% 第1、25、49、73、97位置其他位置都是0
powerdB = [0 -3 -6 -9 -12]; % 信道抽头功率分布(dB)
power = 10.^(powerdB / 10); % 信道抽头功率分布(线性)
ntap = length(powerdB); % 信道抽头数
channel = (randn(1, ntap) + 1i * randn(1, ntap)).* sqrt(power / 2);
delay = [0 24 48 72 96]; % 信道延迟样本 根据每径延时时间计算出的每径延时符号数
lch = delay(end)+1; % 信道长度 信道脉冲响应 (这里为什么加1原因
% 也很简单 因为第一径没有延时,也就是0延时
% 相应对应的就是第一个位置,所以,0延时=>>位置1)
h = zeros(1, lch);
h(delay + 1) = channel; % 最后就得到了多径信道系数