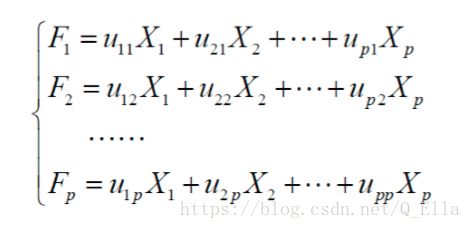多元统计之主成分分析(PCA)
1、基本思想
目标:在保证数据信息丢失最少的前提下,将原来众多具有相关性的指标转化为少数几个相互独立的综合指标。
作用:(1)、解决多重共线性。(2)、将高维数据进行降维处理。
2、数学模型
如下所示数学模型,X1-XP为原始指标,F1-FP为新的主成分,每一个主成分都是原始指标的线性组合,充分反映原始指标的信息,并且相互独立。
模型需要满足的条件:
(1)每个主成分与原始变量的系数的平方和为1。
(2)主成分之间相互独立,主成分之间的协方差为0。
(3)按照主成分的方差依次递减,即按照主成分的重要程度(包含信息量多少)依次递减。
3、几何直观
投影、旋转坐标轴:
旋转的目的:为使原始数据在F1上投影的离散程度最大,即F1的方差最大。
投影的离散化程度越大,即投影误差越小。F1是可以最小化投影误差的平方的方向,描述数据的主要变化。F2是与F1垂直,且除去F1这个方向外,可以最小化投影误差的平方的方向。即椭圆的长轴描述了数据的主要变化,短轴描述了数据的次要变化。
如我们的原始数据为X1和X2两维,可考虑将数据降为1维F1,舍去了次要的一维。
4、内在原理
矩阵分解,这里采用谱分解的方法(也可以用SVD分解)来证明:
谱分解的定理如下所示
我们的目标是获取方差最大的方向,即第一主成分。
下面寻找第二主成分:
因此,我们从矩阵分解的角度证明了主成分分析。每个主成分的系数即对应的特征向量,方差为对应的特征值。
接下来,我们需要决定选择主成分的数量。
定义某个主成分的贡献率为某个主成分的方差在所有方差和中的比重,等价于对应的特征值/特征值之和。
累计贡献率表示前k个主成分共有多大的综合能力,在实际工作中,一般选取累计贡献率>80%的主成分个数。
另外,也可以根据特征值是否大于1来确定主成分的个数。
概念补充:
因子载荷量
原始变量被主成分的提取率
5、具体步骤
(1)由原始数据X的协方差阵,求解出其特征值。
(2)分别求出各个特征值所对应的特征向量。
(3)计算累计贡献率,选择恰当个数的主成分。
(4)将原始数据标准化处理后,计算它在K个主成分上的得分,依次排列。
6、代码实现
R软件:
########################主成分回归###############################
#### read data
mydata=read.csv("***.csv")
mydata=mydata[,-1]
print(mydata)
#### linear model ################################
#标准化时
mydata1=scale(mydata)
lm.sol=lm(y~x1+x2+x3, data=data.frame(mydata1))
summary(lm.sol)
#未标准化时
lm.sol=lm(y~x1+x2+x3, data=mydata)
summary(lm.sol)
library(psych)
#平行分析法选择主成分个数:pc为主成分法,fa为主因子法,both为两者均有
fa.parallel(mydata, fa = "pc", n.iter = 100,
show.legend = FALSE, main = "Scree plot with parallel analysis")
#### principal components analysis ################
#注:cor=T表示用样本的相关矩阵做主成分分析,cor=T表示用样本的协方差阵做主成分分析
mydata.pr=princomp(~x1+x2+x3, data=mydata, cor=T)#cor=T就自带标准化summary(mydata.pr, loadings=TRUE)
#### principal components regression ##############
pre=predict(mydata.pr)
mydata$z1=pre[,1]
#mydata$z2=pre[,2]
lm.sol=lm(y~z1, data=mydata)
summary(lm.sol)
#### transformation ###############################
#主成分的系数
beta=coef(lm.sol)
#原始变量对主成分的系数
A=loadings(mydata.pr)
x.bar=mydata.pr$center
x.sd=mydata.pr$scale
coef=(beta[2]*A[,1])/x.sd
beta0=beta[1]-sum(x.bar*coef)
c(beta0, coef)
SAS软件
data data1;
input x1-x13;
cards;
/*数据省略*/
;
proc princomp out=prin; /*主成分分析模块*/
var x1-x13;
run;
proc print data=prin;
var prin1-prin13;
run;