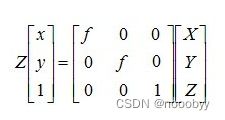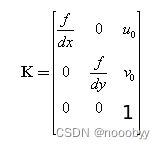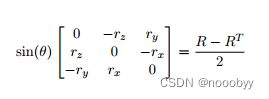计算机视觉 学习笔记（四）相机标定

一、相机标定原理

1.1 基本原理

摄像机标定(Camera calibration)简单来说是从世界坐标系换到图像坐标系的过程，也就是求最终的投影矩阵的过程。

[1]基本的坐标系：

• 世界坐标系；
• 相机坐标系；
• 成像平面坐标系；
• 像素坐标系

[2]一般来说，标定的过程分为两个部分：

• 第一步是从世界坐标系转为相机坐标系，这一步是三维点到三维点的转换，包括R，t（相机外参，确定了相机在某个三维空间中的位置和朝向）等参数；
• 第二步是从相机坐标系转为成像平面坐标系（像素坐标系），这一步是三维点到二维点的转换，包括K（相机内参,是对相机物理特性的近似）等参数；
• 投影矩阵 ： P=K [ R | t ] 是一个3×4矩阵，混合了内参和外参而成。
• 

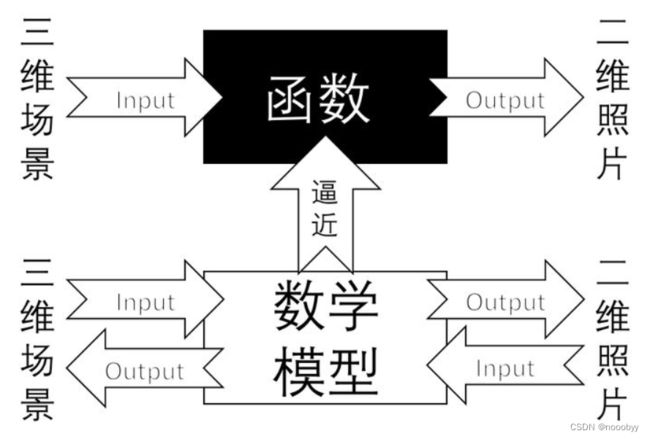
相机标定的目标是我们找一个合适的数学模型，求出这个模型的参数，这样我们能够近似这个三维到二维的过程，使这个三维到二维的过程的函数找到反函数。我们用简单的数学模型来表达复杂的成像过程，并且求出成像的反过程。标定之后的相机，可以进行三维场景的重建，即深度的感知，这是计算机视觉的一大分支。

1.2 相关知识

1、相机模型

这是一个小孔成像的模型，其中：
[1]O点表示camera centre，即相机的中心点，也是相机坐标系的中心点；
[2]z轴表示principal axis，即相机的主轴；
[3]q点所在的平面表示image plane，即相机的像平面，也就是图片坐标系所在的二维平面；
[4]O1点表示principal point，即主点，主轴与像平面相交的点；
[5]O点到O1点的距离，也就是右边图中的f,即相机的焦距；
[6]像平面上的x和y坐标轴是与相机坐标系上的X和Y坐标轴互相平行的；
[7]相机坐标系是以X,Y,Z（大写）三个轴组成的且原点在O点，度量值为米（m）；
[8]像平面坐标系是以x,y（小写）两个轴组成的且原点在O1点，度量值为米（m）；
[9]像素坐标系一般指图片相对坐标系，在这里可以认为和像平面坐标系在一个平面上，不过原点是在图片的角上，而且度量值为像素的个数（pixel）；

2、相机坐标系→成像平面坐标系
[1]以O点为原点建立摄像机坐标系。点Q(X,Y,Z)为摄像机坐标系空间中的一点，该点被光线投影到图像平面上的q(x,y,f)点。
图像平面与光轴z轴垂直，和投影中心距离为f （f是相机的焦距）。按照三角比例关系可以得出：
x/f = X/Z y/f = Y/Z ，即 x = fX/Z y = fY/Z
以上将坐标为(X,Y,Z)的Q点映射到投影平面上坐标为(x,y)的q点的过程称作投影变换。
上述Q点到q点的变换关系用3*3的矩阵可表示为：q = MQ ，其中

最终得出透视投影变换矩阵为：

[1]
M称为摄像机的内参数矩阵，单位均为物理尺寸。

3、成像平面坐标系→像素坐标系
通过下面，可以把像平面坐标系物理单位到像素单位[即→(u,v)]

以图像平面的左上角或左下角为原点建立坐标系。假设像平面坐标系原点位于图像左下角，水平向右为u轴，垂直向上为v轴，均以像素为单位。
以图像平面与光轴的交点O1 为原点建立坐标系，水平向右为x轴，垂直向上为y轴。原点O1一般位于图像中心处，O1在以像素为单位的图像坐标系中的坐标为(u0, v0)。
像平面坐标系和像素坐标系虽然在同一个平面上，但是原点并不是同一个。

设每个像素的物理尺寸大小为 dx * dy (mm) ( 由于单个像素点投影在图像平面上是矩形而不是正方形，因此可能dx != dy)，
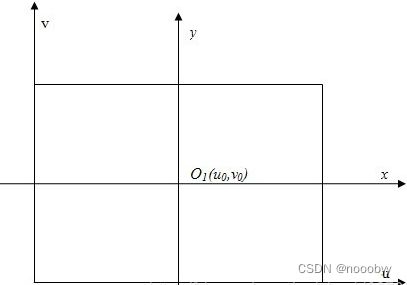
图像平面上某点在成像平面坐标系中的坐标为(x, y)，在像素坐标系中的坐标为(u, v)，则二者满足如下关系：[即(x, y)→(u, v)]
u = x / dx + u0 v = y / dy + v0
用齐次坐标与矩阵形式表示为：

将等式两边都乘以点Q(X,Y,Z)坐标中的Z可得：

将摄像机坐标系中的（1）式代入上式可得：

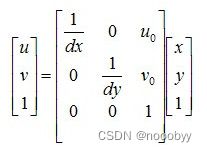
则右边第一个矩阵和第二个矩阵的乘积亦为摄像机的内参数矩阵（单位为像素），相乘后可得：

和（1）式相比，此内参数矩阵中f/dx, f/dy, cx/dx+u0, cy/dy+v0 的单位均为像素。令内参数矩阵为K，则上式可写成：

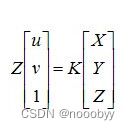
1.3 相机内参k

其中 f 为摄像机的焦距，单位一般是mm;dx,dy 为像元尺寸;u0,v0 为图像中心。
fx = f/dx, fy = f/dy,分别称为x轴和y轴上的归一化焦距.

1.4 畸变参数

1、径向畸变
径向畸变可以通过下面的泰勒级数展开式来校正：

里（x, y）是畸变点在成像仪上的原始位置，r为该点距离成像仪中心的距离，（Xcorrected ，Ycorrected ）是校正后的新位置。

2、切向畸变
如果一个矩形被投影到成像仪上时，
可能会变成一个梯形。切向畸变可以通过如下公式来校正：

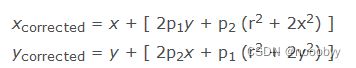
这里（x, y）是畸变点在成像仪上的原始位置，r为该点距离成像仪中心的距离，（Xcorrected ，Ycorrected ）是校正后的新位置。

1.5 相机外参

旋转向量（大小为1×3的矢量或旋转矩阵3×3）和平移向量（tx,ty,tz）。
旋转向量:旋转向量是旋转矩阵紧凑的变现形式，旋转向量为1×3的行矢量。

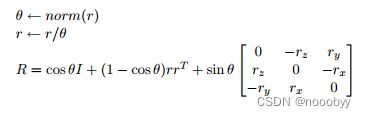
r就是旋转向量，旋转向量的方向是旋转轴 ,旋转向量的模为围绕旋转轴旋转的角度。
通过上面的公式，我们就可以求解出旋转矩阵R。同样的已知旋转矩阵，我们也可以通过下面的公式求解得到旋转向量：

二、代码实现

相机标定的目的：获取摄像机的内参和外参矩阵（同时也会得到每一幅标定图像的选择和平移矩阵），内参和外参系数可以对之后相机拍摄的图像就进行矫正，得到畸变相对很小的图像。
相机标定的输入：标定图像上所有内角点的图像坐标，标定图像上所有内角点的空间三维坐标（通常假定图像位于一个平面上）。
相机标定的输出：摄像机的内参、外参系数。

这三个基础的问题就决定了使用Opencv实现张正友法标定相机的标定流程、标定结果评价以及使用标定结果矫正原始图像的完整流程：

1.准备标定图片
2.对每一张标定图片，提取角点信息
3.对每一张标定图片，提取亚像素角点信息
4.在棋盘标定图上绘制找到的内角点
5.相机标定
6.评价标定结果
7.查看标定效果
我准备的是下图这种格子数为7×5，内角点为6×4的棋盘格图片

import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_MAX_ITER | cv2.TERM_CRITERIA_EPS, 30, 0.001)

# 获取标定板角点的位置
objp = np.zeros((4 * 6, 3), np.float32)
objp[:, :2] = np.mgrid[0:6, 0:4].T.reshape(-1, 2)  # 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y

obj_points = []  # 存储3D点
img_points = []  # 存储2D点

images = glob.glob("camerapic/*.jpg")
i=0;
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    size = gray.shape[::-1]
    ret, corners = cv2.findChessboardCorners(gray, (6, 4), None)
    #print(corners)

    if ret:

        obj_points.append(objp)

        corners2 = cv2.cornerSubPix(gray, corners, (5, 5), (-1, -1), criteria)  # 在原角点的基础上寻找亚像素角点
        #print(corners2)
        if [corners2]:
            img_points.append(corners2)
        else:
            img_points.append(corners)

        cv2.drawChessboardCorners(img, (6, 4), corners, ret)  # 记住，OpenCV的绘制函数一般无返回值
        i+=1;
        cv2.imwrite('conimg'+str(i)+'.jpg', img)
        cv2.waitKey(1500)

print(len(img_points))
cv2.destroyAllWindows()

# 标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(obj_points, img_points, size, None, None)

print("ret:", ret)
print("mtx:\n", mtx) # 内参数矩阵
print("dist:\n", dist)  # 畸变系数   distortion cofficients = (k_1,k_2,p_1,p_2,k_3)
print("rvecs:\n", rvecs)  # 旋转向量  # 外参数
print("tvecs:\n", tvecs ) # 平移向量  # 外参数

print("-----------------------------------------------------")

img = cv2.imread(images[2])
h, w = img.shape[:2]
newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))#显示更大范围的图片（正常重映射之后会删掉一部分图像）
print (newcameramtx)
print("------------------使用undistort函数-------------------")
dst = cv2.undistort(img,mtx,dist,None,newcameramtx)
x,y,w,h = roi
dst1 = dst[y:y+h,x:x+w]
cv2.imwrite('calibresult3.jpg', dst1)
print ("方法一:dst的大小为:", dst1.shape)

运行结果：

2、第二步就是对相机标定

图片数目：15

ret: 1.4748234258734128

内参矩阵（iPhone7plus后置摄像头内置参数矩阵）
mtx:
[[3.28597028e+03 0.00000000e+00 1.52155197e+03]
[0.00000000e+00 3.28046611e+03 1.97821366e+03]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]

畸变矩阵
dist:
[[ 2.15722800e-01 -1.14373758e+00 -1.50403668e-03 3.59889015e-04
1.90438821e+00]]

旋转向量：
rvecs:
[array([[-0.41068525],
[-0.39792937],
[ 1.55001661]]), array([[ 0.16678065],
[-0.17355707],
[ 0.80424154]]), array([[-0.380801 ],
[-0.48092802],
[ 0.60403784]]), array([[-0.50367147],
[ 0.46329121],
[-0.17623549]]), array([[-0.75760729],
[ 0.23383092],
[-0.6949084 ]]), array([[-0.26784188],
[-0.30357258],
[ 1.04894722]]), array([[-0.27920221],
[-0.26068599],
[ 1.52480717]]), array([[-0.07647601],
[-0.64891208],
[ 1.58514325]]), array([[ 0.1807976 ],
[-0.20055577],
[ 1.29838433]]), array([[0.05100636],
[0.01691499],
[1.43421651]]), array([[-0.38577352],
[ 0.12496657],
[ 1.26658523]]), array([[-0.55673024],
[-0.0538189 ],
[ 0.78834763]]), array([[-0.23600261],
[-0.06724515],
[ 1.05855565]]), array([[-0.09113601],
[ 0.00817876],
[ 1.56653157]]), array([[-0.02538916],
[ 0.04568121],
[ 0.01614318]])]

平移向量：
tvecs:
[array([[ 1.89136028],
[-2.4657994 ],
[ 8.36417853]]), array([[-0.28418468],
[-2.84342218],
[ 8.95186298]]), array([[-0.11600086],
[-1.67681554],
[ 9.25847487]]), array([[-3.12343049],
[-1.42958018],
[10.42777939]]), array([[-2.5684328 ],
[ 0.93585532],
[11.52470057]]), array([[ 0.41239482],
[-2.7536404 ],
[ 9.19495801]]), array([[ 1.34367566],
[-2.15969006],
[ 8.95274135]]), array([[ 2.14054344],
[-1.36541065],
[ 7.5066945 ]]), array([[ 1.14463385],
[-2.23291845],
[10.11019762]]), array([[ 0.64385648],
[-2.12159463],
[10.77170956]]), array([[ 0.18098066],
[-3.02154618],
[10.43552702]]), array([[-0.77626273],
[-2.88298209],
[11.19623161]]), array([[-0.11013634],
[-1.59418488],
[10.59346223]]), array([[ 1.34840172],
[-2.22381814],
[10.30140183]]), array([[-2.64570236],
[-1.85315491],
[ 9.43805798]])]

[[3.32460889e+03 0.00000000e+00 1.52234679e+03]
[0.00000000e+00 3.34257886e+03 1.97676019e+03]
[0.00000000e+00 0.00000000e+00 1.00000000e+00]]

畸变矫正：
------------------使用undistort函数-------------------
方法一:dst的大小为: (3826, 2839, 3)

这是原始照片：

矫正后的照片：

以看到，两张照片前后没有什么明显的变化，只是图片进行了轻微的拉伸。可能原图在拍摄时并没有太大的畸变。