单目相机模型

针孔相机模型

针孔相机模型是实际研究中最常用的模型。针孔是一个中间有一个小孔的假想墙壁，光只能从小孔通过。

$f$是摄像机焦距，$Z$是摄像机到物体的距离，$X$是物体长度，是图像平面上的物体长度。由相似三角形可得：
$$-x=f\frac{X}{Z}$$

可将上图等价转换为如下所示系统，图像平面防止在针孔前方的摄像机模型（数学上等价，形式更简单）。

经过转换得到
$$\begin{array}{r}{X}_p=f\frac{X_c}{Z_c}\\ Y_p=f\frac{Y_c}{Z_c}\end{array}⟺Z_c\left[\begin{array}{c}{X}_p\\ Y_p\\ 1\end{array}\right]=\left[\begin{array}{ccc}f& 0& 0\\ 0& f& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]$$

物体投影到成像平面之后由采样器件采样后转换为数字信号，成为像素图像。$\mathrm{d}\mathrm{x},\mathrm{d}\mathrm{y}$分别为一个像素占据的成像平面的物理尺寸(x方向,y方向)。
由于像素坐标系的原点和图像坐标系的原点不同，建模时需要加上两者原点的偏移和$u_0$和$v_0$。
$$\begin{array}{rl}u& =\frac{X_p}{\mathrm{d}\mathrm{x}}+u_0\\ v& =\frac{Y_p}{\mathrm{d}\mathrm{y}}+v_0\end{array}⟺\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{\mathrm{d}\mathrm{x}}& 0& u_0\\ 0& \frac{1}{\mathrm{d}\mathrm{y}}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_p\\ Y_p\\ 1\end{array}\right]$$

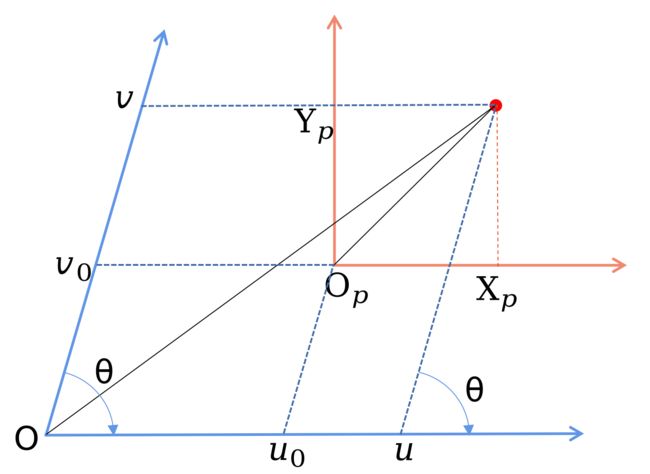
上述推导假设感光板的横轴和纵轴是正交的，但在实际中由于制造精度不会完美正交，假设感光板的横轴与纵轴(像素系的u轴和v轴)的夹角为$\theta$，则模型变为

$$\begin{array}{rl}u& =\frac{X_p}{\mathrm{d}\mathrm{x}}+u_0-\frac{Y_p}{\mathrm{d}\mathrm{x}\tan \theta }\\ v& =\frac{Y_p}{\mathrm{d}\mathrm{y}\sin \theta }+v_0\end{array}⟺\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{\mathrm{d}\mathrm{x}}& -\frac{1}{\mathrm{d}\mathrm{x}\tan \theta }& u_0\\ 0& \frac{1}{\mathrm{d}\mathrm{y}\sin \theta }& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_p\\ Y_p\\ 1\end{array}\right]$$
于是
$$\begin{array}{rl}\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]& =\frac{1}{Z_c}\left[\begin{array}{ccc}\frac{1}{\mathrm{d}\mathrm{x}}& -\frac{1}{\mathrm{d}\mathrm{x}\tan \theta }& u_0\\ 0& \frac{1}{\mathrm{d}\mathrm{y}\sin \theta }& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}f& 0& 0\\ 0& f& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]\\ & =\left[\begin{array}{ccc}\frac{f}{\mathrm{d}\mathrm{x}}& -\frac{f}{\mathrm{d}\mathrm{x}\tan \theta }& u_0\\ 0& \frac{f}{{\mathrm{d}}_{\mathrm{y}}\sin \theta }& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}\frac{X_c}{Z_c}\\ \frac{Y_c}{Z_c}\\ 1\end{array}\right]\end{array}⟺\mathbf{q}=\mathbf{K}\mathbf{x}=\left[\begin{array}{ccc}\alpha & \beta & u_0\\ 0& \gamma & v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]\text{\hspace{1em}(1)}$$

其中$x=\frac{X_c}{Z_c}$和$y=\frac{Y_c}{Z_c}$是归一化坐标(相当于成像与$Z_c=1$平面上)。

通常$\theta$与$90^{\circ }$ 相差很小，当$\theta =90^{\circ }$时，$\gamma =0$，令$\alpha =f_x=\frac{f}{\mathrm{d}\mathrm{x}}$和$\beta =f_y=\frac{f}{\mathrm{d}\mathrm{y}}$是x, y方向的缩放系数，另一种惯例将$u_0$写作$c_x$，$v_0$写作$c_y$，则上式写作：
$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ 0& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

畸变模型

为了获得好的成像效果，通常在相机的前方加上透镜。透镜的引入会对成像过程中光线的传播产生新的影响：一是透镜自身的形状会对光线的传播产生影响，二是在机械组装过程中，透镜和成像平面不完全平行，这也会֯得光线穿过透镜投影到成像面时的位置发生变化。

由透镜形状引起的畸变称为径向畸变 。在针孔模型中，一条直线投影到像素平面上还是一条直线。可是，实际拍摄的照片中，摄像机的透镜往往使得真实环境中的一条直线在图片中变成了曲线。越靠近图像的边缘，这种现象越明显。由于实际加工制作的透镜往往是中心对称的，这使得不规则的畸变通常径向对称。它们主要分为两大类：桶形畸变和枕形畸变，如下图所示。

桶形畸变图像放大率随着与光轴之间的距离增加而减小，而枕形畸变则恰好相反。在这两种畸变中，穿过图像中心和光轴有交点的直线还能保持形状不变。
除了透镜的形状会引入径向畸变，由于在相机的组装过程中不能使透镜和成像面严格平行，所以也会引入切向畸变。

通常选用较为规则的图形例如黑白棋盘格进行相机标定，标定效果较好。使用OpenCV中摄像机标定的相关函数定得出相机内参数$c_x,c_y,f_x,f_y$以及畸变系数$k_1,k_2,k_3$。

对于径向畸变，可以用一个多项式函数来描述畸变前后的坐标变化：这类畸变可以用与距中心的距离有关的二次及高次多项式函数进行拟合。考虑归一化平面上任意一点$\mathbf{p}$，其坐标为$[x,y{]}^T$，是理想成像点(未畸变)的坐标，也可以写成极坐标的形式$[r,\theta {]}^T$，其中$r$表示点与坐标原点之间的距离，$\theta$表示与水平轴的夹角。
$$\begin{gathered} x_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6) \\ {y}_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6) \end{gathered}$$
其中$[x_{distorted},y_{distorted}{]}^T$是畸变后的点的归一化坐标。
上述畸变模型中，对于畸变较小的图像中心区域，畸变校正主要是$k_1$起作用；对于畸变较大的边缘区域，主要是$k_2$起作用。对于切向畸变，可以使用另外的两个参数$p_1$，$p_2$来进行表征：
$$\begin{gathered} x_{distorted}=x+2p_{1}xy+p_2(r^2+2x^2) \\ {y}_{distorted}=y+p_1(r^2+2y^2)+2p_{2}xy \end{gathered}$$
联合上式，对于相机坐标系中的一点P$(x_c,y_c,z_c)$，能够通过5个畸变系数找到这个点在像素平面上的真实位置：

1. 将三维空间点投影到归一化图像平面。设它的归一化坐标为$[x,y{]}^T$。
2. 对归一化平面上的点计算径向畸变和切向畸变。
   $$\{\begin{array}{l}{x}_{distorted}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+2p_{1}xy+p_2(r^2+2x^2)\\ y_{distorted}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+p_1(r^2+2y^2)+2p_{2}xy\end{array}$$
3. 将畸变后的点通过内参数矩阵投影到像素平面，得到该点在图像上的真实位置。
   $$\{\begin{array}{l}u=\alpha x_{distorted}+\gamma y_{distorted}+u_0\\ v=\beta y_{distorted}+v_0\end{array}$$

张正友标定法

张正友标定法利用棋盘格标定，在得到一张标定板的图像之后，利用相应的图像检测算法得到每一个角点的像素坐标$(u,v)$。世界坐标系固定于棋盘格上，则棋盘格上任一点的世界系坐标$Z=0$，由于标定板上每一个格子的大小是已知的，可以计算得到每一个角点在世界坐标系下的坐标$(X,Y,Z)$。利用每一个角点的像素坐标$(u,v)$和每一个角点在世界坐标系下的物理坐标$(X,Y,Z=0)$，来进行相机的标定，获得相机的内外参矩阵、畸变参数。

1. 对每一幅图像得到一个单应性矩阵(像素平面到标定板平面的映射矩阵)$\mathbf{H}$
   内参矩阵设为$\mathbf{K}$，假定模板平面在世界坐标系$Z=0$的平面上，对于一张图片上的每一个角点有
   $$\begin{array}{rl}s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]& =\mathbf{K}\left[\begin{array}{cccc}{\mathbf{r}}_1& {\mathbf{r}}_2& {\mathbf{r}}_3& \mathbf{t}\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z=0\\ 1\end{array}\right]\\ & =\mathbf{K}\left[\begin{array}{ccc}{\mathbf{r}}_1& {\mathbf{r}}_2& \mathbf{t}\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]\end{array}$$
   设单应矩阵
   $$\mathbf{H}=\left[\begin{array}{ccc}{\mathbf{h}}_1& {\mathbf{h}}_2& {\mathbf{h}}_3\end{array}\right]=\mathbf{K}\left[\begin{array}{ccc}{\mathbf{r}}_1& {\mathbf{r}}_2& \mathbf{t}\end{array}\right]$$
   则对于每一个像素点都可以得到一个等式：
   $$\begin{array}{rl}\mathbf{q}& =\frac{1}{s}\mathbf{H}\mathbf{P}\\ \left[\begin{array}{c}u\\ v\\ 1\end{array}\right]& =\frac{1}{s}\mathbf{H}\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]\\ & =\frac{1}{s}\left[\begin{array}{ccc}{H}_{11}& H_{12}& H_{13}\\ H_{21}& H_{22}& H_{23}\\ H_{31}& H_{32}& H_{33}\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]\end{array}$$
   因为使用的是齐次坐标，所以单应矩阵$\mathbf{H}$与尺度无关，可以乘以任意非零因子，因此的自由度是8，然后根据第三行，去掉非零因子，于是有
   $$\{\begin{array}{l}u=\frac{H_{11}X+H_{12}Y+H_{13}}{H_{31}X+H_{32}Y+H_{33}}\\ v=\frac{H_{21}X+H_{22}Y+H_{23}}{H_{31}X+H_{32}Y+H_{33}}\end{array}$$
   最少需要四个角点就可以解出单应矩阵$\mathbf{H}$，求解方法参考。因此，当一张图片上的标定板角点数量等于4时，即可求得该图片对应的矩阵$\mathbf{H}$。当一张图片上的标定板角点数量大于4时，利用最小二乘法回归最佳的矩阵$\mathbf{H}$。

2. 利用约束条件线性求解内参矩阵$\mathbf{K}$
   由旋转矩阵的性质：${\mathbf{r}}_1^T{\mathbf{r}}_2=0,{\mathbf{r}}_1^T{\mathbf{r}}_1=1,{\mathbf{r}}_2^T{\mathbf{r}}_2=1$，得到内参矩阵$\mathbf{K}$的约束条件
   $$\begin{gathered} ({\mathbf{K}}^{-1}{\mathbf{h}}_1{)}^T({\mathbf{K}}^{-1}{\mathbf{h}}_2)=0 \\ ⟹{\mathbf{h}}_1^T{\mathbf{K}}^{-T}{\mathbf{K}}^{-1}{\mathbf{h}}_2=0 \end{gathered}$$
   设
   $$\begin{array}{rl}\mathbf{B}& ={\mathbf{K}}^{-T}{\mathbf{K}}^{-1}=\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ B_{12}& B_{22}& B_{23}\\ B_{13}& B_{23}& B_{33}\end{array}\right]\\ & =\left[\begin{array}{ccc}\frac{1}{{\alpha }^2}& -\frac{\gamma }{{\alpha }^2\beta }& \frac{v_0\gamma -u_0\beta }{{\alpha }^2\beta }\\ -\frac{\gamma }{{\alpha }^2\beta }& \frac{{\gamma }^2}{{\alpha }^2{\beta }^2}+\frac{1}{{\beta }^2}& -\frac{\gamma \left(v_0\gamma -u_0\beta \right)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}\\ \frac{v_0\gamma -u_0\beta }{{\alpha }^2\beta }& -\frac{\gamma \left(v_0\gamma -u_0\beta \right)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}& \frac{{\left(v_0\gamma -u_0\beta \right)}^2}{{\alpha }^2{\beta }^2}+\frac{v_0^2}{{\beta }^2}+1\end{array}\right]\end{array}$$
   $\mathbf{B}$为对称正定矩阵
   则有：
   $$\begin{array}{rl}{\mathbf{h}}_1^T{\mathbf{B}\mathbf{h}}_2& =0\\ {\mathbf{h}}_1^T{\mathbf{B}\mathbf{h}}_1& ={\mathbf{h}}_2^T{\mathbf{B}\mathbf{h}}_2=1\end{array}\text{\hspace{1em}(2)}$$
   上式的几何解释见附录¹。$\mathbf{H}$本身有8个自由度，外参有6个(3个用于旋转，3个用于平移)，因此给定一个单应矩阵$\mathbf{H}$只能提供2个关于内参的约束。
   将$\mathbf{B}$向量化$\mathbf{b}={\left[\begin{array}{cccccc}{B}_{11}& B_{12}& B_{22}& B_{13}& B_{23}& B_{33}\end{array}\right]}^T$， 设${\mathbf{v}}_{ij}={\left[h_{i1}{h}_{j1},h_{i1}{h}_{j2}+h_{i2}{h}_{j1},h_{i2}{h}_{j2},h_{i3}{h}_{j1}+h_{i1}{h}_{j3},h_{i3}{h}_{j2}+h_{i2}{h}_{j3},h_{i3}{h}_{j3}\right]}^T$，则上面三个等式可以化为
   $$\begin{array}{rl}\begin{array}{r}{\mathbf{v}}_{12}^T\mathbf{b}=0\\ \left({\mathbf{v}}_{11}^T-{\mathbf{v}}_{22}^T\right)\mathbf{b}=1\end{array}⟺& \left[\begin{array}{c}{\mathbf{v}}_{12}^T\\ {\mathbf{v}}_{11}^T-{\mathbf{v}}_{22}^T\end{array}\right]\mathbf{b}=0\\ ⟺& \mathbf{V}\mathbf{b}=0\end{array}$$
   根据线性齐次方程组的理论，齐次方程的一个解乘上任意常数依然是方程的解，上述齐次方程的解构成向量空间。既然解是尺度无关的，那我们可以假设$\Vert \mathbf{b}\Vert =1$。每张标定板图片可以提供两个约束方程，n张图片对应的$\mathbf{V}$ 是一个$2\mathrm{n}\times 6$的矩阵。 当$\mathrm{n}⩾3$时，我们可以将解空间缩小至一维，在$\Vert \mathbf{b}\Vert =1$的假设下可以得到唯一解。求解的方法就是计算${\mathbf{V}}^T\mathbf{V}$最小特征值对应的特征向量(也就是$\mathbf{V}$的最小奇异值对应的右奇异向量)：在$\Vert \mathbf{b}\Vert =1$的条件下，求使$\mathbf{V}\mathbf{b}=0$的向量$\mathbf{b}$，也就是使 $\Vert \mathbf{V}\mathbf{b}{\Vert }^2={\mathbf{b}}^T{\mathbf{V}}^T\mathbf{V}\mathbf{b}$的最小的向量$\mathbf{b}$，由Rayleigh商理论可知，${\mathbf{b}}^T{\mathbf{V}}^T\mathbf{V}\mathbf{b}{|}_{\Vert \mathbf{b}\Vert =1}$的最小值是${\mathbf{V}}^T\mathbf{V}$的最小特征值，$\mathbf{b}$对应的特征向量。
   求解出的$\mathbf{B}$矩阵是尺度无关的，可以乘以任意非零因子，因此$\mathbf{B}=\lambda {\mathbf{K}}^{-T}{\mathbf{K}}^{-1}$，可从中导出内参矩阵$\mathbf{K}$，求解过程见附录²，再由$\mathbf{K}$和单应矩阵$\mathbf{H}$计算外参$\mathbf{R}$和$\mathbf{t}$：
   $$\left[\begin{array}{ccc}{\mathbf{r}}_1& {\mathbf{r}}_2& \mathbf{t}\end{array}\right]=\lambda {\mathbf{K}}^{-1}\mathbf{H}$$
   其中$\lambda =\frac{1}{\Vert {\mathbf{K}}^{-1}{\mathbf{h}}_1}\Vert =\frac{1}{\Vert {\mathbf{K}}^{-1}{\mathbf{h}}_2\Vert }$
   完整的外参矩阵为$\left[\begin{array}{cccc}{\mathbf{r}}_1& {\mathbf{r}}_2& {\mathbf{r}}_3& \mathbf{t}\end{array}\right]$ 。但是，由于张正友标定板将世界坐标系的$\mathrm{x}\mathrm{O}\mathrm{y}$平面选取在棋盘格上，则棋盘格上任一点的世界坐标$Z=0$ ，因此，${\mathbf{r}}_3$ 在坐标转化中并没有作用。但是 ${\mathbf{r}}_3$要使得满足旋转矩阵的性质，即列与列之间单位正交，因此可以通过向量${\mathbf{r}}_1,{\mathbf{r}}_2$的叉乘计算得到，即
   $${\mathbf{r}}_3={\mathbf{r}}_1\times {\mathbf{r}}_2$$
   由于数据存在噪声，所以计算得到的$\left[\begin{array}{ccc}{\mathbf{r}}_1& {\mathbf{r}}_2& {\mathbf{r}}_3\end{array}\right]$ 可能并不满足旋转矩阵的条件，使用附录³的方法可以由一个普通三维矩阵估计出最优的旋转矩阵。

3. 最大似然估计
   上述解决方案是通过最小化代数距离得到的，这在物理上是没有意义的。我们可以通过最大似然估计来进一步优化，上述方案的解作为初值。
   
   $$\underset{\mathbf{K},{\mathbf{R}}_i,{\mathbf{t}}_i}{\mathrm{argmin}}\sum _{i=1}^n\sum _{j=1}^m\Vert {\mathbf{q}}_{ij}-\hat{\mathbf{q}}(\mathbf{K},{\mathbf{R}}_i,{\mathbf{t}}_i,{\mathbf{P}}_j){\Vert }^2\text{\hspace{1em}(opt1)}$$
   其中$\hat{\mathbf{q}}(\mathbf{K},{\mathbf{R}}_i,{\mathbf{t}}_i,{\mathbf{P}}_j)$是图像i中的棋盘格角点${\mathbf{P}}_j$的重投影像素。上式本质上是最小化重投影误差的非线性最小二乘问题，可以使用Levenberg-Marquardt优化算法求解。

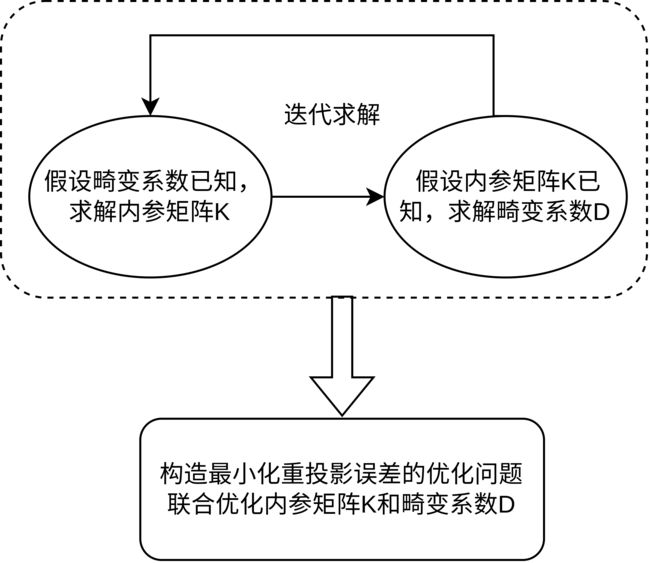
4. 迭代求解畸变系数
   目前为止我们还没有考虑畸变，这是因为张正友标定法采用迭代求解的思路，在求解$\mathbf{K},{\mathbf{R}}_i,{\mathbf{t}}_i$的时候假设畸变已知，求解出$\mathbf{K},{\mathbf{R}}_i,{\mathbf{t}}_i$之后再求解畸变参数，如此反复迭代。
   设世界系下的棋盘格角点$\mathbf{P}$经过理想针孔模型投影(无畸变)后的像素坐标为$(u,v)$，$(\breve{u},\breve{v})$是真实观测到的对应像素坐标点。类似的，$(x,y)$和$(\breve{x},\breve{y})$分别是理想的(无畸变)和真实的(有畸变)的归一化坐标。则根据畸变模型
   
   $$\{\begin{array}{l}\breve{x}=x(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+2p_{1}xy+p_2(r^2+2x^2)\\ \breve{y}=y(1+k_1{r}^2+k_2{r}^4+k_3{r}^6)+p_1(r^2+2y^2)+2p_{2}xy\end{array}\text{\hspace{1em}(3)}$$
   整理成畸变系数的线性方程形式：
   $$\left(\begin{array}{ccccc}x{r}^2& x{r}^4& x{r}^6& 2xy& r^2+2x^2\\ y{r}^2& y{r}^4& y{r}^6& r^2+2y^2& 2xy\end{array}\right)\left(\begin{array}{c}{k}_1\\ k_2\\ k_3\\ p_1\\ p_2\end{array}\right)=\left(\begin{array}{c}\breve{x}-x\\ \breve{y}-y\end{array}\right)$$
   其中$r=\sqrt{x^2+y^2}$，可由$\left[\begin{array}{c}\breve{u}\\ \breve{v}\\ 1\end{array}\right]=\mathbf{K}\left[\begin{array}{c}\breve{x}\\ \breve{y}\\ 1\end{array}\right]$从$(\breve{u},\breve{v})$计算出$(\breve{x},\breve{y})$
   给定n张图片，每张图片有m对对应点，每一对对应点都可以得到上面两个等式，将所有2mn个等式合并，设畸变向量$\mathbf{d}=[k_1,k_2,k_3,p_1,p_2{]}^T$写成矩阵形式：
   $$\mathbf{A}\mathbf{d}=\mathbf{a}$$
   线性最小二乘解为：
   $$\mathbf{d}=({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{a}$$
   求解出畸变系数之后，按照(3)式将原优化问题$(\mathrm{o}\mathrm{p}\mathrm{t}1)$中的$\hat{\mathbf{q}}$替换为$\breve{\mathbf{q}}=(\breve{x},\breve{y}{)}^T$，优化求解$\mathbf{K},{\mathbf{R}}_i,{\mathbf{t}}_i$，再执行步骤4.求解畸变系数，如此反复迭代，直到收敛。

5. 完整的最大似然估计：
   在步骤3.的基础上将畸变系数考虑进去，构建更大规模的最大似然估计问题：
   $$\underset{\mathbf{K},\mathbf{d},{\mathbf{R}}_i,{\mathbf{t}}_i}{\mathrm{argmin}}\sum _{i=1}^n\sum _{j=1}^m\Vert {\mathbf{q}}_{ij}-\hat{\mathbf{q}}(\mathbf{K},\mathbf{d},{\mathbf{R}}_i,{\mathbf{t}}_i,{\mathbf{P}}_j){\Vert }^2\text{\hspace{1em}(opt2)}$$
   其中$\hat{\mathbf{q}}(\mathbf{K},\mathbf{d},{\mathbf{R}}_i,{\mathbf{t}}_i,{\mathbf{P}}_j)$是图像i中的棋盘格角点${\mathbf{P}}_j$的重投影像素。上式本质上是最小化重投影误差的非线性最小二乘问题，可以使用Levenberg-Marquardt优化算法求解。步骤4.求得的畸变系数可以作为优化问题的初值。

我们定义一个正交矩阵$\mathbf{Z}={\mathbf{V}}^T{\mathbf{R}}^T\mathbf{U}$，则
$$\begin{array}{rl}\mathrm{t}\mathrm{r}({\mathbf{R}}^T\mathbf{Q})& =\mathrm{t}\mathrm{r}({\mathbf{R}}^T{\mathbf{U}\mathbf{\Sigma }\mathbf{V}}^T)\\ & =\mathrm{t}\mathrm{r}({\mathbf{V}}^T{\mathbf{R}}^T\mathbf{U}\mathbf{\Sigma })\\ & =\mathrm{t}\mathrm{r}(\mathbf{Z}\mathbf{\Sigma })=\sum _{i=1}^3{z}_{ii}{\sigma }_i⩽\sum _{i=1}^3{\sigma }_i\end{array}$$
显然，等式成立的条件是$\mathbf{Z}=\mathbf{I}⟹\mathbf{R}={\mathbf{U}\mathbf{V}}^{\mathbf{T}}$

参考资料

A Flexible New Technique for Camera Calibration
知乎-张正友标定法

---

1. 内参约束(2)的几何解释
   棋盘格平面上一点由世界坐标系到相机坐标系的转换关系式:
   $$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{r}}_1& {\mathbf{r}}_2& \mathbf{t}\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]=X{\mathbf{r}}_1+Y{\mathbf{r}}_2+\mathbf{t}$$
   则棋盘格平面在相机坐标系下是由${\mathbf{r}}_1$和${\mathbf{r}}_2$张成的向量空间(平面)加上一个偏移$\mathbf{t}$组成。
   由于${\mathbf{r}}_3$与${\mathbf{r}}_1$和${\mathbf{r}}_2$正交，故该平面的法向量与${\mathbf{r}}_3$共线
   $${\mathbf{r}}_3^T\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\end{array}\right]={\mathbf{r}}_3^T(X{\mathbf{r}}_1+Y{\mathbf{r}}_2+\mathbf{t})={\mathbf{r}}_3^T\mathbf{t}$$
   使用齐次坐标的形式重塑平面方程：
   $${\left[\begin{array}{c}{\mathbf{r}}_3\\ {\mathbf{r}}_3^T\mathbf{t}\end{array}\right]}^T\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ w\end{array}\right]=0$$
   当$w=0$时代表无穷远点，当 $w=1$时代表其他。
   这个平面与无穷远平面相交于一条线，并且易得$\left[\begin{array}{c}{\mathbf{r}}_1\\ 0\end{array}\right]$和$\left[\begin{array}{c}{\mathbf{r}}_2\\ 0\end{array}\right]$是相交线上的两个特殊点。相交线上的任意点都可以表示为这两点的线性组合：
   $${\mathbf{p}}_{\infty }=a\left[\begin{array}{c}{\mathbf{r}}_1\\ 0\end{array}\right]+b\left[\begin{array}{c}{\mathbf{r}}_2\\ 0\end{array}\right]=\left[\begin{array}{c}a{\mathbf{r}}_1+b{\mathbf{r}}_2\\ 0\end{array}\right]$$ ↩︎

2. 从矩阵$\mathbf{B}$提取内参
   求解出的$\mathbf{B}$矩阵与尺度无关，可以乘以任意非零因子
   $$\begin{array}{rl}\mathbf{B}& =\lambda {\mathbf{K}}^{-T}{\mathbf{K}}^{-1}=\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ B_{12}& B_{22}& B_{23}\\ B_{13}& B_{23}& B_{33}\end{array}\right]\\ & =\lambda \left[\begin{array}{ccc}\frac{1}{{\alpha }^2}& -\frac{\gamma }{{\alpha }^2\beta }& \frac{v_0\gamma -u_0\beta }{{\alpha }^2\beta }\\ -\frac{\gamma }{{\alpha }^2\beta }& \frac{{\gamma }^2}{{\alpha }^2{\beta }^2}+\frac{1}{{\beta }^2}& -\frac{\gamma \left(v_0\gamma -u_0\beta \right)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}\\ \frac{v_0\gamma -u_0\beta }{{\alpha }^2\beta }& -\frac{\gamma \left(v_0\gamma -u_0\beta \right)}{{\alpha }^2{\beta }^2}-\frac{v_0}{{\beta }^2}& \frac{{\left(v_0\gamma -u_0\beta \right)}^2}{{\alpha }^2{\beta }^2}+\frac{v_0^2}{{\beta }^2}+1\end{array}\right]\end{array}$$
   可以唯一的提取出相机内参：
   $$\begin{array}{rl}{v}_0& =\frac{B_{12}{B}_{13}-B_{11}{B}_{23}}{B_{11}{B}_{22}-B_{12}^2}\\ \lambda & =B_{33}-\frac{B_{13}^2+v_0\left(B_{12}{B}_{13}-B_{11}{B}_{23}\right)}{B_{11}}\\ \alpha & =\sqrt{\frac{\lambda }{B_{11}}}\\ \beta & =\sqrt{\frac{\lambda B_{11}}{B_{11}{B}_{22}-B_{12}^2}}\\ \gamma & =-\frac{B_{12}{\alpha }^2\beta }{\lambda }\\ u_0& =\frac{\gamma v_0}{\beta }-\frac{B_{13}{\alpha }^2}{\lambda }\end{array}$$ ↩︎

3. 由普通矩阵近似旋转矩阵
   给定一个普通的$3\times 3$矩阵$\mathbf{Q}$，求解出一个最优的旋转矩阵$\mathbf{R}$来近似它。这里，最优的定义事使$\mathbf{R}-\mathbf{Q}$的Frobenius范数最小：
   $$\underset{\mathbf{R}}{\min }\Vert \mathbf{R}-\mathbf{Q}{\Vert }_F^2\mathrm{s}.\mathrm{t}.{\mathbf{R}}^{\mathrm{T}}\mathbf{R}=\mathbf{I}$$
   因为
   $$\begin{array}{rl}\Vert \mathbf{R}-\mathbf{Q}{\Vert }_F^2& =\mathrm{t}\mathrm{r}\left((\mathbf{R}-\mathbf{Q}{)}^T(\mathbf{R}-\mathbf{Q})\right)\\ & =3+\mathrm{t}\mathrm{r}\left({\mathbf{Q}}^T\mathbf{Q}\right)-2\mathrm{t}\mathrm{r}({\mathbf{R}}^T\mathbf{Q})\end{array}$$
   于是问题简化为最大化$\mathrm{t}\mathrm{r}({\mathbf{R}}^T\mathbf{Q})$
   设$\mathbf{Q}$的奇异值分解为：
   $$\mathbf{Q}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^T$$
   其中$\mathbf{\Sigma }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\sigma }_1,{\sigma }_2,{\sigma }_3)$，对角线元素为奇异值。 ↩︎