LeetCode_动态规划_困难_1691.堆叠长方体的最大高度

1.题目

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [width_i, length_i, height_i]（下标从 0 开始）。请你从 cuboids 选出一个子集 ，并将它们堆叠起来。

如果 width_i <= width_j 且 length_i <= length_j 且 height_i <= height_j，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。

返回堆叠长方体 cuboids 可以得到的最大高度。

示例 1：

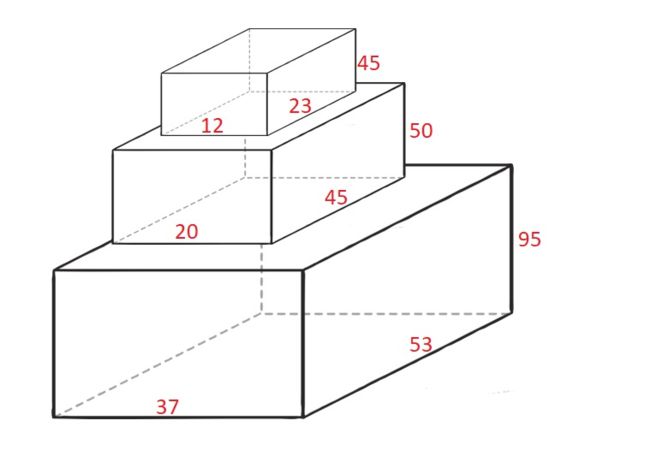
输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
输出：190
解释：
第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
总高度是 95 + 50 + 45 = 190 。

示例 2：
输入：cuboids = [[38,25,45],[76,35,3]]
输出：76
解释：
无法将任何长方体放在另一个上面。
选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。

示例 3：
输入：cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]]
输出：102
解释：
重新排列长方体后，可以看到所有长方体的尺寸都相同。
你可以把 11x7 的一面朝下，这样它们的高度就是 17 。
堆叠长方体的最大高度为 6 * 17 = 102 。

提示：
n == cuboids.length
1 <= n <= 100
1 <= width_i, length_i, height_i <= 100

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/maximum-height-by-stacking-cuboids

2.思路

（1）排序 & 动态规划
思路参考该 LeetCode 用户题解。

3.代码实现（Java）

//思路1————排序 & 动态规划
class Solution {
    public int maxHeight(int[][] cuboids) {
        int res = 0;
        int n = cuboids.length;
        for (int[] cuboid : cuboids) {
            //升序排序
            Arrays.sort(cuboid);
        }
        Arrays.sort(cuboids, (c1, c2) -> 
            (c1[0] != c2[0]) ? (c1[0] - c2[0]) : (c1[1] != c2[1] ? c1[1] - c2[1] : c1[2] - c2[2])
        );
        // dp[i] 表示排序后的前 i 个长方体，将第 i 个长方体置于底部时的最大堆叠高度
        int[] dp = new int[n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                //排序后的 cuboids[j][0] <= cuboids[i][0] 恒成立
                if (cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2]) {
                    // cuboids[j] 可以堆在 cuboids[i] 上
                    dp[i] = Math.max(dp[i], dp[j]);
                }
            }
            dp[i] += cuboids[i][2];
            res = Math.max(dp[i], res);
        }
         return res;
    }
}