python+OpenCV笔记(三十九):离散傅里叶变换(DFT)
目录
一、什么是傅里叶变换
二、代码编写:傅里叶变换与逆傅里叶变换
【一、OpenCV实现傅里叶变换】
【二、OpenCV实现逆傅里叶变换】
【三、Numpy实现傅里叶变换】
【四、Numpy实现逆傅里叶变换】
三、应用实践:低通滤波与高通滤波
一、低通滤波
二、高通滤波
一、什么是傅里叶变换
- 傅里叶原理表明:任何连续测量的时序或信号,都可以表示为不同频率的正弦波信号的无限叠加。也就是说,傅里叶变换是一种特殊的积分变换,它能将满足一定条件的某个函数表示成正弦基函数的线性组合或者积分。
不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。
(看一张动态图,原作者:傅里叶分析之掐死教程(完整版)更新于2014.06.06 - 知乎) (动态图的开始部分很清晰的展现了:红色曲线可以由众多条(或者无数条)蓝色的正弦函数以及余弦函数叠加而成)
- (再看一张老面孔) 在数字图像领域,我们一般使用的都是二维的灰度图像,所以这里从二维的傅里叶变换说起。
(1)首先,先看时域图像,他是我们经常见到与接触的一种函数,称它为 f(t): 从大图中可以看到,这条线是由所有的正弦波叠加而成的总和,反过来说就是,所有的正弦波都是这条总和波的分量。其中,频率最低的排在最前面,越往后,频率越高(即上下跳动越活越),并且,每一条波的振幅都不同(因为波形的高度不同)。同时,我们也发现在所有的正弦波中,有很多分量是直线,那是因为时域图像中的 f(t) 并不需要某种特定频率的正弦波,所以表现为直线。
(2)接下来,我们从正弦波的侧面看过去,便是 f(t) 在频域的样子(终于到这一步了) 在频域上,自变量为正弦波分量的频率,因变量为振幅,他们两形成的函数 F(w),也就是频域图像。这时,一个时域——频域的映射就完成了。
(3)让我们在回顾一下文章开头的动图的最后一张: 由 时域上的红色图像 映射到了 频域上的蓝色图像,这便是傅里叶变换所做的事。
- 离散傅里叶变换在图像处理领域的应用:
对于数字图像这种离散的信号,频率大小表示信号变化的剧烈程度或者说是信号变化的快慢。频率越大,变化越剧烈,频率越小,信号越平缓,对应到图像中,高频信号往往是图像中的边缘信号和噪声信号,而低频信号包含图像变化频繁的图像轮廓及背景等信号。
因此,我们可以做相应的锐化和模糊的处理:提出其中的高频分量做傅里叶逆变换得到的就是锐化的结果(高通滤波器)。 提出其中的低频分量做傅里叶逆变换得到的就是模糊的结果(低通滤波器)。
另外,需要特别注意的一点是:
截取频域图中的任何一个区域对应的都是原来的整张图的区域,而不是对应的局部
二、代码编写:傅里叶变换与逆傅里叶变换
【Numpy与OpenCV均可实现傅里叶变换与逆傅里叶变换】
【一、OpenCV实现傅里叶变换】
| OpenCV API: | |
| dst = cv2.dft (src , flags) | |
| 参数:
|
其他函数:
- np.fft.fftshift(dst):将图像的低频部分移动到图像的中心
- 返回值 = cv2.magnitude(参数1, 参数2)——将复数结果转换为幅值
参数1:浮点型X坐标值,也就是实部
参数2:浮点型Y坐标值,也就是虚部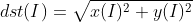
【代码编写】
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 以灰度形式读入
img = cv2.imread('img\qiqiqi.png', 0)
# 使用cv2.dft()进行傅里叶变换
dst = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
# 将变换后图像的低频部分转移到图像的中心
dst_center = np.fft.fftshift(dst)
# 使用cv2.magnitude将实部和虚部转换为实部,乘以20是为了使得结果更大
result = 20 * np.log(np.abs(cv2.magnitude(dst_center[:, :, 0], dst_center[:, :, 1])))
# 显示图像
plt.subplot(121)
plt.imshow(img, cmap="gray")
plt.axis("off")
plt.subplot(122)
plt.axis("off")
plt.imshow(result, cmap="gray")
plt.show()
【二、OpenCV实现逆傅里叶变换】
| OpenCV API | |
| dst= cv2.idft(src) | |
参数:
|
其他函数:
(同 【一、OpenCV实现傅里叶变换】)
【代码编写】
# %%opencv实现逆傅里叶变换
# 以灰度形式读入
img = cv2.imread('img\qiqiqi.png', 0)
# 使用cv2.dft()进行傅里叶变换
dst = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
# 将变换后图像的低频部分转移到图像的中心
dst_center = np.fft.fftshift(dst)
#
# 中间可以定义相应的掩膜去留高频或者低频部分
#
# 使用np.fft.ifftshift将低频移动到原来的位置
dst_origin = np.fft.ifftshift(dst_center)
# 使用cv2.idft进行傅里叶的逆变化
img_idft = cv2.idft(dst_origin)
# 使用cv2.magnitude转化为空间域内
img_idft = cv2.magnitude(img_idft[:, :, 0], img_idft[:, :, 1])
# 显示图像
plt.subplot(121)
plt.imshow(img, cmap="gray")
plt.axis("off")
plt.title('原图')
plt.subplot(122)
plt.axis("off")
plt.imshow(img_idft, cmap=plt.cm.gray)
plt.title('逆傅里叶变换')
plt.show()【三、Numpy实现傅里叶变换】
| Numpy | |
| np.fft.fft2(img) | |
参数:
|
其他函数:
(可参照 【一、OpenCV实现傅里叶变换】)
【代码编写】
# %%NumPy实现傅里叶变换
img = cv2.imread('img//qiqiqi.png', 0)
# 使用Numpy进行傅里叶变换
f = np.fft.fft2(img)
# 无处理(未把零频率分量移到中间)
mid_result = 20 * np.log(np.abs(f))
# 把零频率分量移到中间
fshift = np.fft.fftshift(f)
result = 20 * np.log(np.abs(fshift))
# 显示图像
plt.subplot(131)
plt.imshow(img, cmap="gray")
plt.axis("off")
plt.title('原图')
plt.subplot(132)
plt.axis("off")
plt.imshow(mid_result, cmap=plt.cm.gray)
plt.title('Numpy傅里叶变换\n(未把零频率分量移到中心)')
plt.subplot(133)
plt.axis("off")
plt.imshow(result, cmap=plt.cm.gray)
plt.title('Numpy傅里叶变换\n(把零频率分量移到中心)')
plt.tight_layout()
plt.show()【四、Numpy实现逆傅里叶变换】
| Numpy | |
| np.fft.ifft2(img) | |
参数:
|
【代码编写】
# %%Numpy实现逆傅里叶变换
img = cv2.imread('img//qiqiqi.png', 0)
# 进行傅里叶变换
f = np.fft.fft2(img)
# 逆傅里叶变换
f_center = np.fft.ifftshift(f)
f_origin = np.fft.ifft2(f_center)
# 设置区间
f_origin = np.abs(f_origin)
# 显示图像
plt.subplot(121)
plt.imshow(img, cmap="gray")
plt.axis("off")
plt.title('原图')
plt.subplot(122)
plt.axis("off")
plt.imshow(f_origin, cmap=plt.cm.gray)
plt.title('Numpy逆傅里叶变换')
plt.show()三、应用实践:低通滤波与高通滤波
一、低通滤波
——模糊图像(使用OpenCV)
【代码编写】
# %%OpenCV低通滤波
img = cv2.imread('img//qiqiqi.png', 0)
dft = cv2.dft(np.float32(img), flags=cv2.DFT_COMPLEX_OUTPUT)
dft_center = np.fft.fftshift(dft)
# 定义掩模:生成的掩模中间为1周围为0
crow, ccol = int(img.shape[0] / 2), int(img.shape[1] / 2) # 求得图像的中心点位置
mask = np.zeros((img.shape[0], img.shape[1], 2), np.uint8)
mask[crow - 30:crow + 30, ccol - 30:ccol + 30] = 1
# 将掩模与傅里叶变化后图像相乘,保留中间部分
mask_img = dft_center * mask
img_idf = np.fft.ifftshift(mask_img)
img_idf = cv2.idft(img_idf)
img_idf = cv2.magnitude(img_idf[:, :, 0], img_idf[:, :, 1])
plt.subplot(121)
plt.axis('off')
plt.imshow(img, cmap='gray')
plt.subplot(122)
plt.axis('off')
plt.imshow(img_idf, cmap='gray')
plt.show()二、高通滤波
——锐化图像(使用OpenCV)
【代码编写】
将低通滤波的定义的掩膜由 中间0周围1 改为 中间1周围0 即可
# 定义掩模:生成的掩模中间为0周围为1
crow, ccol = int(img.shape[0] / 2), int(img.shape[1] / 2) # 求得图像的中心点位置
mask = np.ones((img.shape[0], img.shape[1], 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 0