密码学(1)RSA与AES算法原理
什么是RSA
在1977年,Ron Rivest, Adi Shami和Leonard Adleman这三个人开发了一个新的算法,并用他们三个名字的首字母来命名这个算法,这个算法名叫RSA
非对称加密与对称加密
RSA算法采用的是非对称加密,假如我有你的公钥,我想给你发一个加密的消息,我可以利用你的公钥来加密我的消息, 然后你就可以用你的私钥来解密
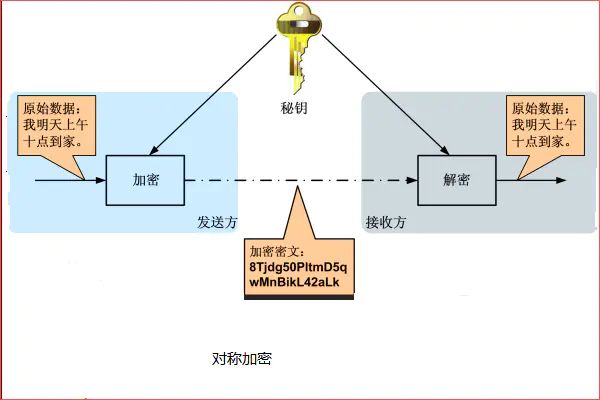
而对称加密则是要双方都拥有同一个私钥,才能进行解密
RSA与AES
RSA使用的是非对称加密,AES使用的是对称加密,那他们俩有什么区别呢?
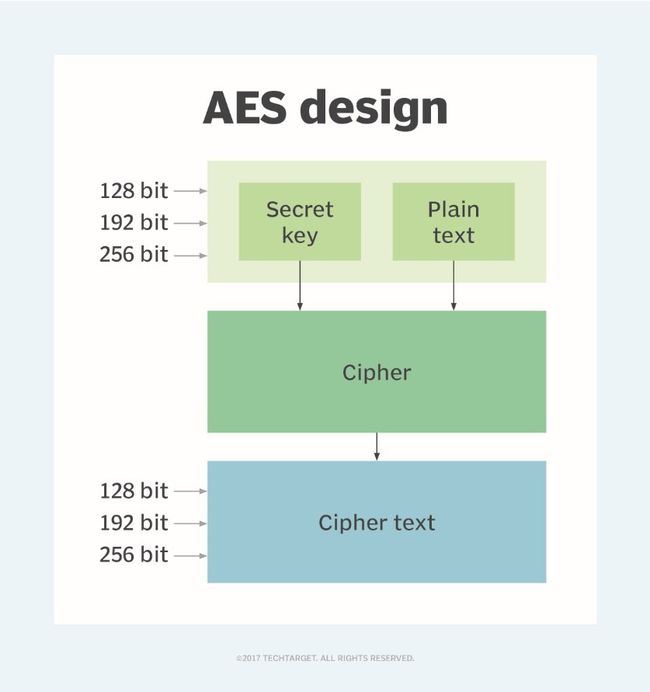
AES
假如我们使用AES加密一个文件
首先我们会生成一个随机的128位或192位或256位的密钥,然后通过AES加密算法来加密文件
接收方要使用相同的密钥才能解密消息,AES比RSA要快一些,因为AES是一种分组密码,简单来说它就是一个美化版的字节混合器,首先AES将数据划分成块,然后会进一步划分这个块并处理字节
AES的关键操作是对字节替换和混合,这和RSA不一样
RSA
RSA是进行基本的数学运算,你要加密的消息越大,数字就越大,这就是为什么AES比RSA快
ABC --> \x41\x42\x43 --> 0x414243 --> 4276803
ascii hex hex转dec
加密
https://en.wikipedia.org/wiki/RSA_(cryptosystem)
![]()
c:加密后的消息
e:公钥
m:需要加密的消息
n:公钥
RSA会对消息进行一个数学运算,这个公式很简单,跟高中数学差不多
((0x414243)^e %n) = c
解密
![]()
d:私钥
(c)^d %n = 0x414243
进行这两个运算非常依赖e和d,也就是公钥与私钥,如果我们e作为消息的幂运算并模n,然后再用d作为幂进行运算并模n,就会得到原消息
((0x414243)^e)^d %n = 0x414243
mod n
mod是什么意思呢,假如我们有一个钟表,时针指向的是3,那么12小时后指向的是几呢,结果还是3
12 + 3 =15
15 % 12 = 3
而这个12就是mod 12,取余数
在之前的运算中,如果不进行mod运算,我们会得到一个非常大的数字
((0x414243)^e)^d = 114514.........312331....313
进行mod运算后,就会变成很小的数字
((0x414243)^e)^d = 114514.........312331....313
mod n = 0x414243
RSA的密钥生成
首先看看RSA的密钥生成过程
如果要生成RSA密钥,首先需要两个大质数,p和q,这两个质数必须是随机的,然后使用p乘以q,得到n,也就是上面算术使用的mod n,n也是公钥的一部分,这也是为什么n是公开的,它只是两个数的乘积,并且我们也很难通过因数分解来得到原来的q和p,因为p和q都是随机的,并且是质数,而且非常大
现在得到了公钥n,接下来我们要看看私钥d部分
φ(n) = n - (p + q -1)
d ≡ e^−1 (mod φ(n))
这是公钥e的生成过程
e是一个大于1小于φ(n)的随机数,e通常设置为65537,因为当随机选择更大的数字时,加密效率会大大降低
RSA算法简单演示
加密
首先我们需要将字符转换为数字
B --> 2
![]()
然后对这个数字进行运算,这里需要e和n,假设e是5,n是14,方程式就是这样的
2^5 (mod 14) == 32 (mod 14) = 4
加密后的密文就为4
解密
解密我们需要私钥d以及公钥n
d ≡ e^−1 (mod φ(n))
这里d通过计算得到11,n还是14
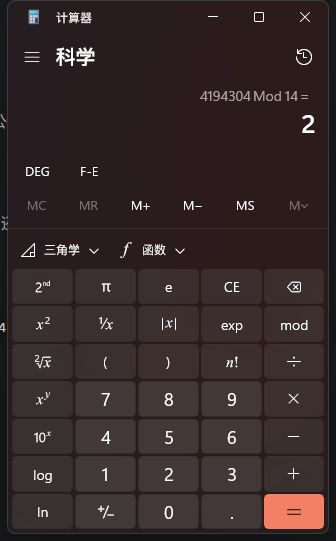
![]()
4^11(mod 14) == 4194304(mod14)
最终运算结果为2,转换为字符就是B