Logistic回归——梯度提升算法

1. Logistic 回归定义

1.1 主要思想

假设现在有一些数据点，我们用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程称为回归。利用Logistic回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。

训练分类器时的做法就是寻找最佳拟合参数，使用的是最优化算法。

1.2 Logistic 回归的一般过程

（1）收集数据：采用任意方法收集数据。
（2）准备数据：由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳。
（3）分析数据：采用任意方法对数据进行分析。
（4）训练算法：大部分时间将用于训练，训练的目的是为了找到最佳的分类回归系数。
（5）测试算法：一旦训练步骤完成，分类将会很快。
（6）使用算法：首先，我们需要输入一些数据，并将其转换为对应的结构化数值；接着，基于训练好的回归系数就可以对这些数值进行简单的回归计算，判定它们属于哪个类别；在这之后，我们就可以在输出的类别上做一些其他分析工作。

1.3 一些最优化算法

包括基本的梯度上升法和一个改进的随机梯度上升法。这些优化算法将用于分类器的训练。

2. Logistic回归与sigmoid 函数

在两个类的情况下，海维赛德阶跃函数（或称单位阶跃函数）输出0或1，但该函数的问题在于：在跳跃点上从0瞬间跳跃到1，这个瞬间跳跃过程有时很难处理，于是，有个另外一个函数——Sigmoid函数，格式为：

sigmoid函数在不同坐标尺度下的两条曲线图如下。当$x$为0时，sigmoid函数值为0.5.随着$x$的增大，对应的sigmoid值将逼近于1；而随着$x$的减小，sigmoid值将逼近于0。当横坐标足够大时，sigmoid函数看起来像一个阶跃函数。

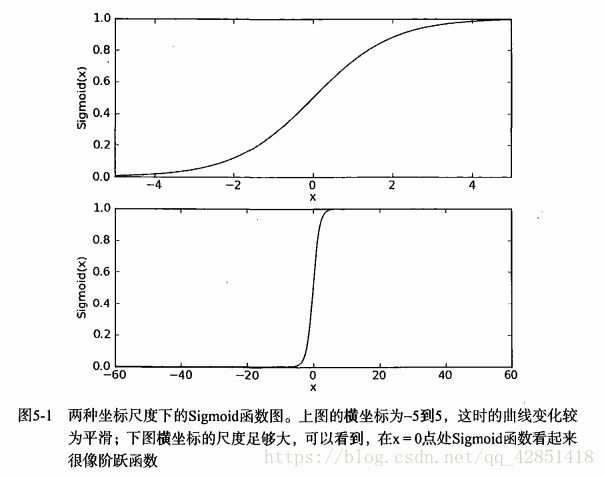
因此，为了实现Logistic回归分类器，我们可以在每个特征上乘以一个回归系数，然后把结果值带入sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5的即被归入0类。所以，Logistic回归也可以被看出是一种概率估计。

那么，确定了分类器的函数形式之后，现在的问题变成了：如何确定最佳回归系数？

3. 基于最优化方法的最佳回归系数确定

sigmoid函数的输入记为$z$，由以下公式得出：
$$z=w_0{x}_0+w_1{x}_1+w_2{x}_2+\cdot \cdot \cdot +w_n{x}_n$$
采用向量的写法，即为：$z=w^{T}x$。其中，向量$x$是分类器的输入数据，向量$w$是我们要找到的最佳参数（最佳系数），从而使得分类器尽可能地精确。

为了寻找最佳参数，需要用到一些最优化的理论知识。

下面将介绍梯度上升法的最优化方法，使用该方法求得数据集的最佳参数。接下来，展示如何绘制该算法产生的决策边界图（即最佳分界线），该图将梯度上升法的分类效果可视化呈现出来。最后，将学习随机梯度上升算法，以及如何改进获得更好的结果。

3.1 第一个最优化算法——梯度上升法

3.1.1 基本思想

要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。

函数$f(x,y)$的梯度由下式表示：

这个梯度意味着要沿着$x$的方向移动

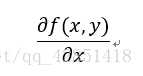
，沿$y$的方向移动

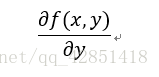
其中，函数$f(x,y)$必须要在待计算的点上有定义并且可微。
梯度算子总是指向函数值增长最快的方向，这里说的是移动方向，而未提到移动量的大小。该量值称为步长，记作$alpha$，用向量来表示的话，梯度算法的迭代公式为：

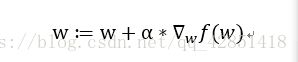
该公式将一直被迭代执行，直到达到某个停止条件为止，比如：迭代次数达到某个指定值或算法达到某个可以允许的误差范围。

3.1.2 梯度上升法的伪代码：

{ 每个回归系数初始化为1
重复R次：
计算alpha*gradient更新回归系数的向量
返回回归系数
}

数据集（testSet.txt）：100个样本点，每个点包含两维数值型特征：第一列X1（看作x轴上的值）和第二列X2（看作y轴上的值）。第三列数据即为分类标签（格式如下）。根据标签的不同，对这些点进行分类。

### Logistic回归梯度上升优化算法
import numpy as np
import matplotlib.pyplot as plt

"""
函数说明：加载数据
输入参数：
    无
返回值：
    dataMat--数据列表
    labelMat--标签列表
"""

def loadDataSet():	#主要功能：打开文本文件testSet.txt并逐行读取
    dataMat=[]															 #创建数据列表
    labelMat=[]															 #创建标签列表
    fr=open('testSet.txt')  											 #打开文件
    for line in fr.readlines():  										 #逐行读取
        lineArr=line.strip().split()   									 #去回车，放入列表
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])]) 	     #添加数据（每行前两个值分别为X1和X2，第三个值是数据对应的类别标签）。此外，为了计算方便，该函数还将X0的值设为1.0
        labelMat.append(int(lineArr[2]))   								 #添加标签
    fr.close() 															 #关闭文件
    return dataMat,labelMat 											 #返回

"""
函数说明:绘制数据集
输入参数：
    无
返回值：
    无
"""

def plotDataSet():
    dataMat, labelMat = loadDataSet()                                   #加载数据集
    dataArr = np.array(dataMat)                                         #转换成numpy的array数组
    n = np.shape(dataMat)[0]                                            #数据个数
    xcord1 = []; ycord1 = []                                            #正样本
    xcord2 = []; ycord2 = []                                            #负样本
    for i in range(n):                                                  #根据数据集标签进行分类
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])    #1为正样本
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])    #0为负样本
    fig = plt.figure()
    ax = fig.add_subplot(111)                                           #添加subplot
    ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#绘制正样本
    ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)            #绘制负样本
    plt.title('DataSet')                                                #绘制title
    plt.xlabel('x'); plt.ylabel('y')                                    #绘制label
    plt.show()                                                          #显示

"""
函数说明：sigmoid函数
输入参数：
    inX--数据
返回值：
    sigmoid函数
"""

def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))

"""
函数说明：梯度上升算法
输入参数：
    dataMatIn--数据集
    classLabels--数据标签
返回值：
    weights.getA()--求得的权重数组（最优参数）
"""

def gradAscent(dataMatIn,classLabels):					#第一个参数是一个2维Numpy数组，每列分别代表每个不同的特征，每行则代表每个训练样本。 如：我们采用的是100个样本的简单数据集，包含了两个特征X1和X2，再加上第0维特征X0，所以dataMathIn里存放的将是100*3的矩阵。第二个参数是类别标签，它是一个1*100的行向量。为了便于矩阵计算，需要将该行向量转换为列向量，做法是将原向量转置，再将它赋值给labelMat
    dataMatrix=np.mat(dataMatIn)      							 #转化为Numpy矩阵数据类型
    labelMat=np.mat(classLabels).transpose()  				     #转化为Numpy的mat，并进行转置
    m,n=np.shape(dataMatrix)       								 #返回dataMatrix的大小。m为行数，n为列数。
    alpha=0.001   											     #移动步长，也就是学习速率，控制更新的幅度。
    maxCycles=500	#迭代次数
    weights=np.ones((n,1))
    for k in range(maxCycles):
        h=sigmoid(dataMatrix*weights)   						 #梯度上升矢量化公式。注意：这里的h不是一个数，而是一个列向量，列向量的元素个数等于样本个数，这里是100。对应的，dataMatrix*weights这个运算代表的也不止一次乘积运算，事实上该运算包含了300次的乘积。
        error=labelMat-h   #真实类别与预测类别的差值
        weights=weights+alpha*dataMatrix.transpose()*error       #矩阵相乘。按差值的方向调整回归系数
    return weights.getA()   									 #将矩阵转换为数组，返回权重数组

3.2 改进算法——随机梯度上升算法

3.2.1 算法思想

梯度上升算法在每次更新回归系数时，都需要遍历整个数据集，该法在处理小数据集时尚可，但如果数据集很庞大，那么该法的计算复杂度就太高了。因此，一种改进的方法是一次仅对一个样本点来更新回归系数，该法称为随机梯度上升算法。该法是一个在线学习算法，因为可以在新样本到来时，对分类器进行增量式更新。

3.2.2 伪代码

{ 所有回归系数初始化为1
对数据集中每个样本：
计算该样本的梯度
使用alpha*gradient更新回归系数
返回回归系数值
}

"""
函数说明：随机梯度上升算法
输入参数：
    dataMat--数据
    class Labels--数据标签
返回值：
    weights--权重参数数组（最优参数）
"""

def stocGradAscent0(dataMatrix,classLabels):    #与梯度上升法相比，一，后者的变量h和误差error都是向量，而该算法中则全是数值；
    #二，该算法没有矩阵的转换过程，所有变量的数据类型都是Numpy数组。
    m,n=np.shape(dataMatrix)
    alpha=0.01
    weights=np.ones(n)
    for i in range(m):
        h=sigmoid(sum(dataMatrix[i]*weights))
        error=classLabels[i]-h
        weights=weights+alpha*error*dataMatrix[i]
    return weights

3.3 改进二——改进的随机梯度上升算法

随机梯度上升算法中，有些系数需要迭代很多次才能达到稳定值，且在大的系数波动停止后，还有一些小的周期性波动，产生这种现象的原因是存在一些不能正确分类的样本点，即数据集并不是线性可分的，在每次迭代时候这些样本点就会引发系数的剧烈改变。而我们期望的算法是能够避免这种来回的波动，从而收敛到某个值，另外，收敛速度也需要更快。

对于这个问题，可修改随机梯度上升算法，得以解决。代码如下：

"""
函数说明：改进的随机梯度上升算法
输入参数：
    dataMatrix--数据
    classLabels--数据标签
    numIter--迭代次数
返回值：
    weights--权重参数数组（最优参数）
"""
def stocGradAscent1(dataMatrix,classLabels,numIter=150):    #改进处：增加了一个迭代次数作为第3个参数。
    # 如果该参数没有给定的话，算法将默认迭代150次。如果给定，那么算法将按照新的参数进行迭代。
    m,n=np.shape(dataMatrix)
    weights=np.ones(n)
    for j in range(numIter):
        dataIndex=list(range(m))
        for i in range(m):
            alpha=4/(1.0+j+i)+0.01   #改进一：alpha在每次迭代的时候都会调整。这会缓解回归系数的数据波动或者高频波动。另外，虽然alpha会随着迭代次数不断减小，但永远不会减小到0，因为其中还存在一个常数项。
            # 必须这样做的原因是为了保证在多次迭代之后新数据仍然具有一定的影响。如果要处理的问题是动态变化的，那么可以适当加大上述常数项，来确保新的值获得更大的回归系数。
            # 另外一点值得注意的是，在降低alpha的函数中，alpha每次减少1/（j+i），其中j是迭代次数，i是样本点的下标。这样当j<

改进后的算法，一，回归系数没有出现周期性波动，这归功于该改进算法中的样本随机选择机制。二，当系数收敛时，迭代次数更少，这是因为改进算法可以收敛得更快。这次仅对数据集做了20次遍历，而之前的方法是500次。

3.4 结果

三种算法的结果可视化如下：

"""
函数说明：绘制数据集
输入参数：
    weights - 权重参数数组
返回值：
    无
"""
def plotBestFit(weights):		#上述函数已经解出了一组回归系数，它确定了不同类别数据之间的分隔线。
    dataMat, labelMat = loadDataSet()                                   #加载数据集
    dataArr = np.array(dataMat)                                         #转换成numpy的array数组
    n = np.shape(dataMat)[0]                                            #数据个数
    xcord1 = []; ycord1 = []                                            #正样本
    xcord2 = []; ycord2 = []                                            #负样本
    for i in range(n):                                                  #根据数据集标签进行分类
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])    #1为正样本
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])    #0为负样本
    fig = plt.figure()
    ax = fig.add_subplot(111)                                           #添加subplot
    ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#绘制正样本
    ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)            #绘制负样本
    x = np.arange(-3.0, 3.0, 0.1)
    y = (-weights[0] - weights[1] * x) / weights[2]                     #最佳拟合直线。
	#解释该公式：该处设置了sigmoid函数为0，0是两个分类（类别1和类别0）的分界处，因此，设定0=w0x0+w1x1+w2x2,然后解出X1和X2的关系式（即上代码中x和y的关系式）（即分隔线的方程，注意X0=1），得：x2=(-w0-w1x1)/w2
    ax.plot(x, y)
    plt.title('BestFit')                                                #绘制title
    plt.xlabel('X1'); plt.ylabel('X2')                                  #绘制label
    plt.show()

def main():
    dataArr, labelMat = loadDataSet()
    # print(dataMat)
    # print(labelMat)
    plotDataSet()
    weights1 = gradAscent(dataArr, labelMat)     #1.梯度上升算法
    print(weights1)
    plotBestFit(weights1)

    dataArr, labelMat = loadDataSet()
    weights2 = stocGradAscent0(np.array(dataArr), labelMat)      #2.随机梯度上升算法
    print(weights2)
    plotBestFit(weights2)

    dataArr, labelMat = loadDataSet()
    weight3 = stocGradAscent1(np.array(dataArr), labelMat)   #3.改进的随机梯度上升算法
    print(weight3)
    plotBestFit(weight3)


if __name__ == '__main__':
    main()

结果：
（1）绘制的数据集：

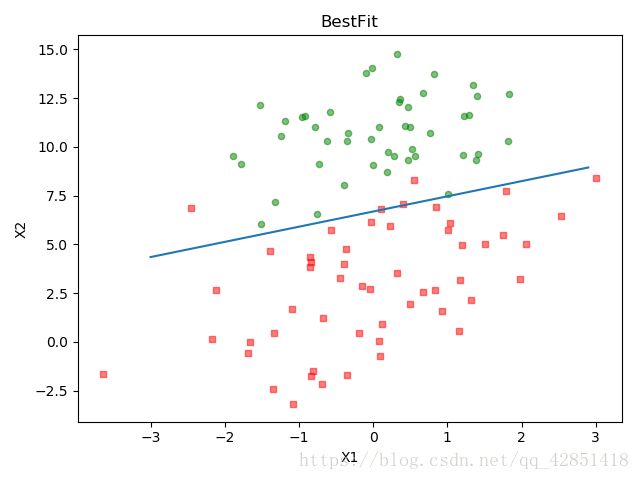
（2）三种算法下，数据集的分类结果如下：
1.梯度上升算法

回归系数：

[[ 4.12414349]
 [ 0.48007329]
 [-0.6168482 ]]

分类结果：

2.随机梯度上升算法

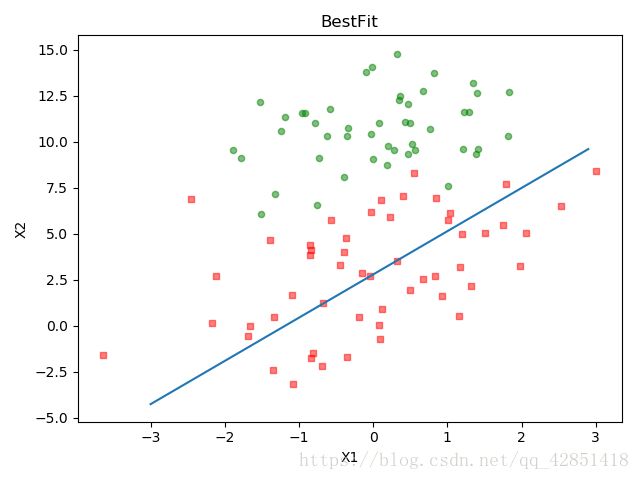
回归系数：

[ 1.01702007  0.85914348 -0.36579921]

分类结果：

3.改进的随机梯度上升算法

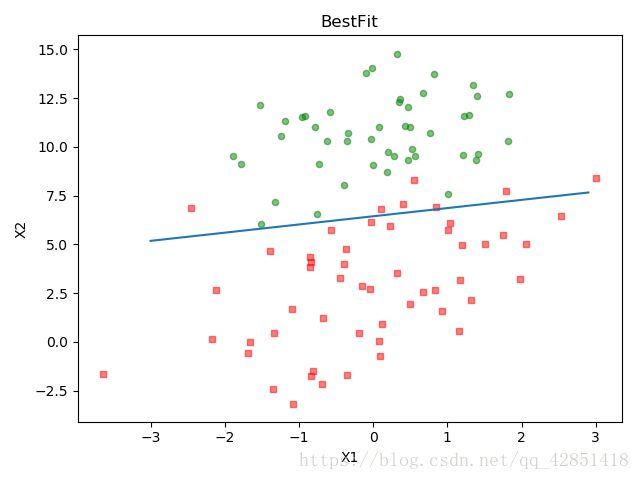
回归系数：

[14.09184834  1.12253583 -2.02502699]

分类结果：

另外，当数据集中存在缺失值时，我们可以用一个实数值来替换，因为Numpy数据类型不允许包含缺失值。这里选择实数0来替换所有的缺失值。这样做的原因是：我们需要一个在更新时不会影响系数的值，因此回归系数的更新公式如下：
$$weights=weights+alpha\ast error\ast dataMatrix[randIndex]$$
如果$dataMatrix$的某特征对应值为0，那么该特征的回归系数将不做更新，即：
$$weights=weights$$
另外，由于$sigmoid(0)=0.5$，即它对结果的预测不具有任何倾向性，因此上述做法也不会对误差项造成任何影响。基于上述原因，将缺失值用0值代替既可以保留现有数据，也不需要对优化算法进行修改。此外，该数据集中的特征取值一般不为0，因此在某种意义上说它满足“特殊值”这个要求。