MATLAB2016笔记(九):概率统计( 概率密度、统计作图、统计特征、累积概率分布、随机变量产生)
文章目录
- 一、产生随机变量
-
- (一)二项分布随机数据的产生 binornd
- (二)正态分布随机数据的产生 normrnd
- (三)常见分布随机数据的产生
- 二、概率密度计算
-
- (一)通用函数概率密度值 pdf / ksdensity
- (二)专用函数概率密度值
- 三、累积概率分布
-
- (一)通用函数累积概率值 cdf / ksdensity
- (二)专用函数累积概率值
- 四、统计特征
-
- (一)平均值、中位数、忽略NaN的中位数、几何平均数、调和平均数
- (二)数据比较 普通排序sort、按行排序sortrows、求解值域大小range
- (三)期望(即算术平均值mean)
- (四)方差 var、标准差 std
- (五)协方差 cov、相关系数 corrcoef
- 五、统计作图
-
- (一)正整数频率表 tabulate
- (二)累积分布函数图形 cdfplot
- (三)最小二乘拟合直线 lsline
- (四)绘制正态分布概率图形 normplot
- (五)样本数据的箱线图 boxplot
- (六)参考线绘制 refline / refcurve
- (七)样本概率图形 capaplot / capability
- (八)正态拟合直方图 histfit
一、产生随机变量
(一)二项分布随机数据的产生 binornd
P { X = k } = ( n k ) p k ( 1 − p ) n − k P\{X=k\}=(_{n}^{k})p^k(1-p)^{n-k} P{X=k}=(nk)pk(1−p)n−k
binornd函数可以产生二项分布随机数据,其格式如下:
R=binornd(N,P) N,P为二项分布参数,N,P可以是大小相同的向量、矩阵或多维数组;R与N,P具有相同的大小
R=binornd(N,P,m,n,...) 当N,P为标量时,可以由m,n...控制输出的个数以及维数
R=binornd(N,P,[m,n,...]) 与上功能相同
根据实践,发现当仅有参数m,且N、P为标量时,输出结果为m*m的随机数矩阵
(二)正态分布随机数据的产生 normrnd
f ( x ) = 1 2 π σ e x p ( − ( x − μ ) 2 2 σ 2 ) f(x)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2}) f(x)=2πσ1exp(−2σ2(x−μ)2)
normrnd函数可以产生正态分布随机数据,其格式如下:
R = normrnd(mu,sigma)
R = normrnd(mu,sigma,m,n,...)
R = normrnd(mu,sigma,[m,n,...])
具体用法与binornd一致
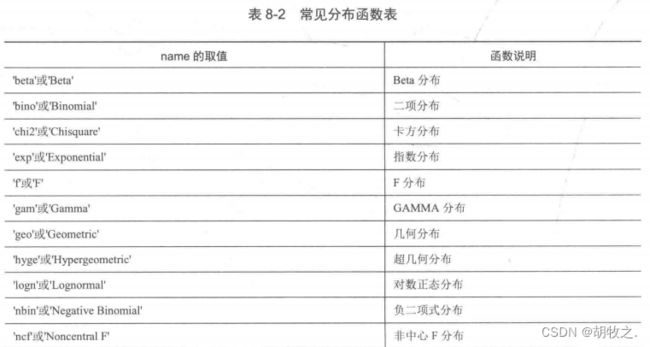
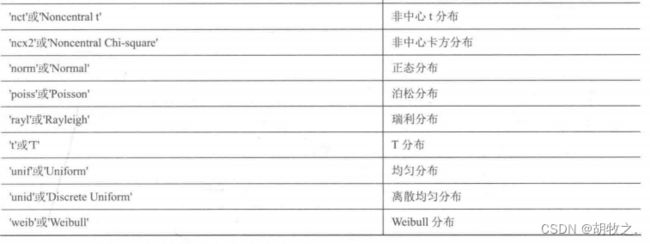
(三)常见分布随机数据的产生
二、概率密度计算
(一)通用函数概率密度值 pdf / ksdensity
1.pdf函数
pdf函数计算概率密度,其格式如下:
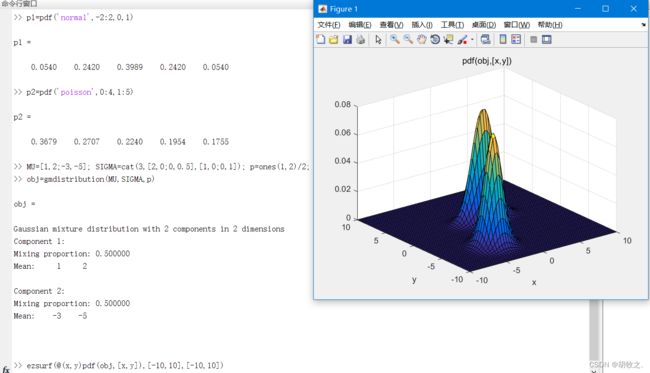
y = pdf('name',x,A)
y = pdf('name',x,A,B)
y = pdf('name',x,A,B,C)
y = pdf('name',x,A,B,C,D) name为分布函数名,A、B、C、D为参数的值(不同分布的参数个数不同),函数将返回在x处的概率密度值
y = pdf(obj,x) obj为高斯联合分布对象
2.ksdensity函数
对单变量或多变量的核平滑化函数估计,在连续分布样本上表现最好
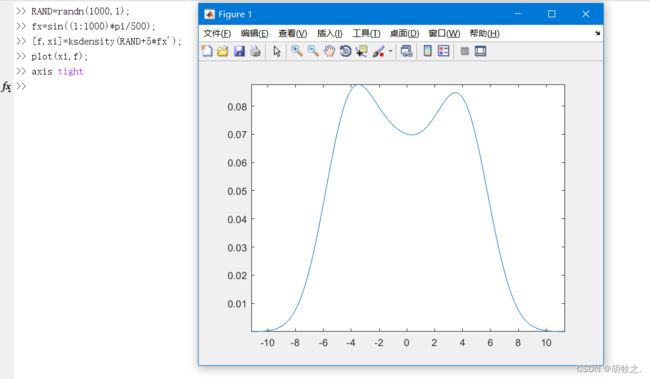
使用ksdensity函数求取一般函数/数据的概率密度函数,该函数的调用格式如下:
[f,xi] = ksdensity(x)
[f,xi] = ksdensity(x,pts)
[f,xi] = ksdensity(x,pts,Name,Value) x为待统计的向量;xi为计算概率密度的点;f为得到的概率密度;Name和Value为可选属性及其属性值
[f,xi,bw] = ksdensity(___) bw,核平滑化窗口的带宽
ksdensity(___)
ksdensity(ax,___) ax指定绘制位置坐标轴对象
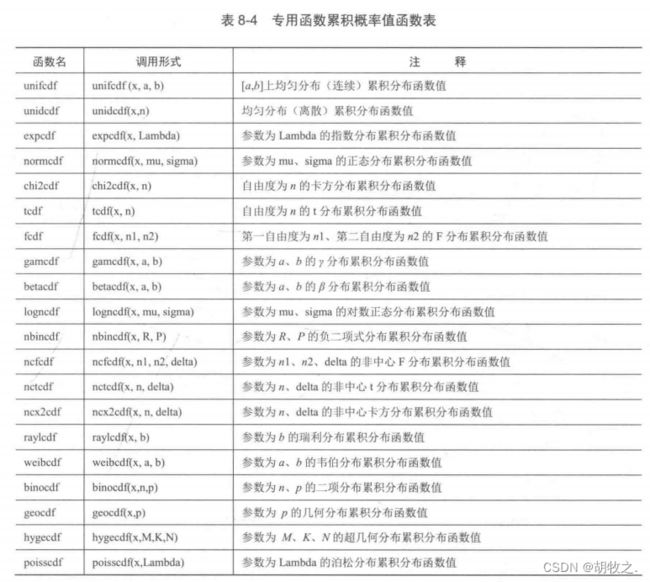
(二)专用函数概率密度值
三、累积概率分布
(一)通用函数累积概率值 cdf / ksdensity
1.cdf函数
使用cdf函数可以计算随机变量 x ≤ X x \leq X x≤X的概率之和(累积概率和),其调用格式如下:
y = pdf('name',x,A)
y = pdf('name',x,A,B)
y = pdf('name',x,A,B,C)
y = pdf('name',x,A,B,C,D) name为分布函数名,A、B、C、D为参数的值(不同分布的参数个数不同)
y = pdf(obj,x) obj为高斯联合分布对象
参数含义与pdf一致
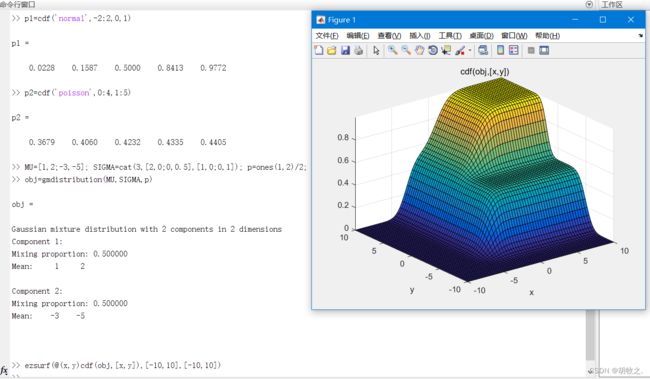
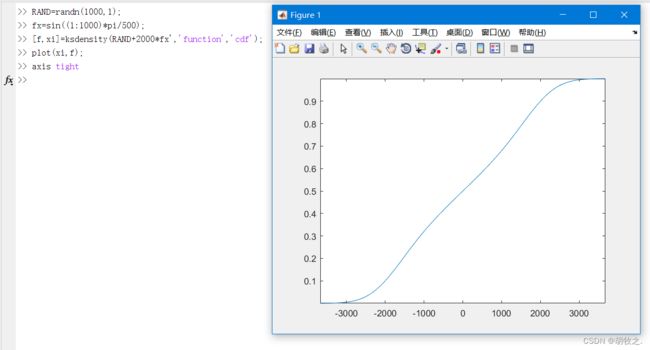
2.ksdensity函数
ksdensity函数默认求取概率密度值,如果要计算累积概率分布,需要设置其属性function的取值为cdf
(二)专用函数累积概率值
四、统计特征
(一)平均值、中位数、忽略NaN的中位数、几何平均数、调和平均数
1.平均值——mean函数
平均数,数据之和除以数据个数,其具体用法如下:
M = mean(A) 若A为向量,返回一个值;若A为矩阵,返回每列的均值
M = mean(A,dim) 返回沿着对应维度的均值,例如A为矩阵时,dim为2可以返回每行的均值
M = mean(___,outtype) 以特定数据类型返回均值
M = mean(___,nanflag) nanflag为一个选项,为‘includenan’,均值计算包括NaN;‘omitnan’,均值计算不包括NaN
2.中位数——median函数
中位数,按顺序排列的一组数据中居于中间位置的数,若观察值有偶数个,通常取中间两个数的平均值作为中位数
其具体用法如下
M = median(A)
M = median(A,dim)
M = median(___,nanflag)
参数含义与mean函数相同
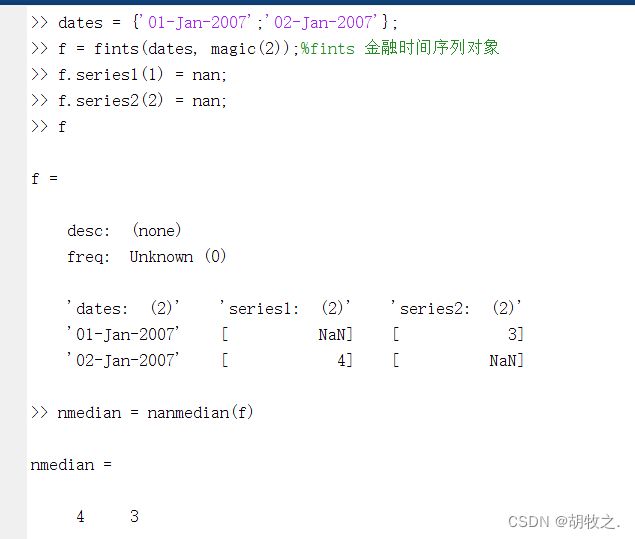
3.忽略NaN的中位数——nanmedian函数
m = nanmedian(X)
m = nanmedian(X,DIM)
参数含义同上
4.几何平均数——geomean函数
G = X 1 × X 2 × . . . × X n n = ∏ i = 1 n X i n G=\sqrt[n]{X_1\times X_2\times ...\times X_n }=\sqrt[n]{\prod_{i=1}^{n}X_i} G=nX1×X2×...×Xn=ni=1∏nXi
其具体用法如下:
m = geomean(x)
geomean(X,dim)
参数含义同上
5.调和平均数——harmmean函数
调和平均数(harmonic mean)又称倒数平均数,是总体各统计变量倒数的算术平均数的倒数
H n = 1 1 n ∑ i = 1 n 1 x i = n ∑ i = 1 n 1 x i H_n=\frac{1}{\frac{1}{n}\sum_{i=1}^{n}\frac{1}{x_i}}=\frac{n}{\sum_{i=1}^{n}\frac{1}{x_i}} Hn=n1∑i=1nxi11=∑i=1nxi1n
其用法如下
m = harmmean(X)
harmmean(X,dim)
参数含义同上
(二)数据比较 普通排序sort、按行排序sortrows、求解值域大小range
数据排序是指由数据比较引发的各种数据操作,常见的操作包括普通排序(sort)、按行排序(sortrows)、求解值域大小(range)
1.普通排序——sort函数
其用法如下
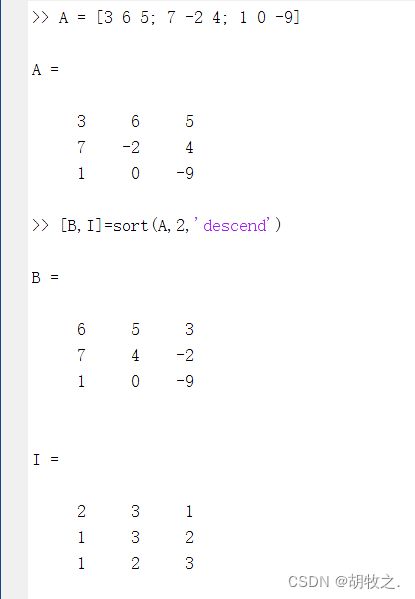
B = sort(A) 如果A是向量,直接排序;若A是矩阵,仅对列排序
B = sort(A,dim) 沿着对应维度进行排序,例如A为矩阵时,dim为2可以对每行进行排序
B = sort(___,direction) direction为选项,控制具体排序方法,'ascend'(默认)为递增,'descend'为递减
[B,I] = sort(___) I与A大小相同,表示排序后的元素在A中的索引值
2.按行排序——sortrows函数
其用法如下
B = sortrows(A) A为矩阵,对A的不同行按ASCII码字典序排序(默认递增):比较相同列,进行排序,相等再比较下一列,
B = sortrows(A,column) 对特定的列进行比较,若有两行的对应列均相等,则保持相对位置不变
[B,index] = sortrows(___) 返回排序后每一行原来的行号
3.求解值域大小——range函数
range函数将返回最大值与最小值之间的差值
其用法如下
range(X) range会忽略NaN
y = range(X,dim)
参数含义同上
(三)期望(即算术平均值mean)
(四)方差 var、标准差 std
1.方差——var函数
总体方差: σ 2 = ∑ ( X − μ ) 2 N \sigma^2=\frac{\sum(X-\mu)^2}{N} σ2=N∑(X−μ)2
样本方差: s 2 = ∑ ( X − X ˉ ) 2 n − 1 s^2=\frac{\sum(X-\bar{X})^2}{n-1} s2=n−1∑(X−Xˉ)2
其用法如下
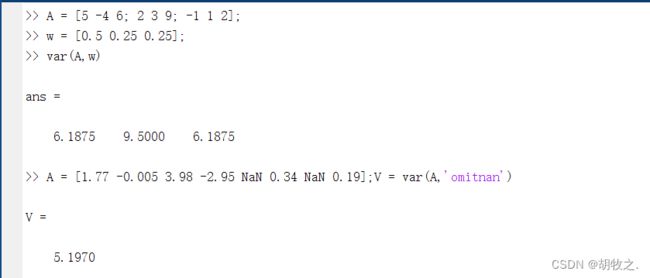
V = var(A)
V = var(___,w) w默认为0,结果为样本方差,即除以(n-1);w=1时为总体方差,除以N;w还可以为权值数组,要求w与A大小相同
V = var(___,dim)
V = var(___,w,dim)
V = var(___,nanflag)
其余参数与之前一致
2.标准差——std函数
标准差是方差的算术平方根,标准差能反映一个数据集的离散程度
其用法如下
S = std(A)
S = std(A,w)
S = std(A,w,dim)
S = std(___,nanflag)
参数含义同上
(五)协方差 cov、相关系数 corrcoef
1.协方差——cov函数
在概率论和统计学中,协方差用于衡量两个变量的总体误差,而方差是协方差的一种特殊情况,即当两个变量是相同的情况
C o v ( X , Y ) = E [ ( X − E ( X ) ) ( Y − E ( Y ) ) ] = E ( X Y ) − 2 E ( X ) E ( Y ) + E ( X ) E ( Y ) = E ( X Y ) − E ( X ) E ( Y ) Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=E(XY)-2E(X)E(Y)+E(X)E(Y)=E(XY)-E(X)E(Y) Cov(X,Y)=E[(X−E(X))(Y−E(Y))]=E(XY)−2E(X)E(Y)+E(X)E(Y)=E(XY)−E(X)E(Y)
C o v ( X , Y ) = ∑ i = 1 n ( X i − X ˉ ) ( Y i − Y ˉ ) n − 1 Cov(X,Y)=\frac{\sum_{i=1}^{n}(X_i-\bar{X})(Y_i-\bar{Y})}{n-1} Cov(X,Y)=n−1∑i=1n(Xi−Xˉ)(Yi−Yˉ)
如果 X X X与 Y Y Y是统计独立的,那么二者之间的协方差就是 0 0 0,因为两个独立的随机变量满足 E ( X Y ) = E ( X ) E ( Y ) E(XY)=E(X)E(Y) E(XY)=E(X)E(Y)
但 X X X与 Y Y Y的协方差为 0 0 0,二者并不一定是统计独立的
其用法如下
C = cov(A) 当A为向量时,cov(A)与var(A)结果相同;若A为n*m的矩阵,将返回n*n的协方差矩阵,C(i,j)表示第i个变量(第i列)与第j个变量的协方差
C = cov(A,B)
C = cov(___,w) w可为0或1,含义与之前相同
C = cov(___,nanflag)
2.相关系数——corrcoef函数
r ( X , Y ) = C o v ( X , Y ) V a r ( X ) V a r ( Y ) r(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}} r(X,Y)=Var(X)Var(Y)Cov(X,Y)
其用法如下
R = corrcoef(A)
R = corrcoef(A,B) 格于协方差相同
[R,P] = corrcoef(___) P值矩阵用于测试被观测现象没有关系的假设(原假设),如果 P 的非对角线元素小于显著性水平(默认值为 0.05),则 R 中的相应相关性被视为显著。如果 R 包含复数元素,则此语法无效。
[R,P,RL,RU] = corrcoef(___) 这些矩阵包含每个系数的 95% 置信区间的下界和上界。如果 R 包含复数元素,则此语法无效
___ = corrcoef(___,Name,Value) Name为参数,value为该参数对应的值,用于控制输出
如:corrcoef(A,'alpha',0.1) ,置信区间为90%
corrcoef(A,'rows','complete'),省略 A 的包含一个或多个NaN值的行
五、统计作图
(一)正整数频率表 tabulate
其具体用法如下
tbl = tabulate(x) 若x为数值数组,tbl也将为数值矩阵;如果x是分类变量、字符数组或字符串单元数组,tbl也将为单元数组
tbl的第一列为x中的值,第二列为每类值的总个数,第三列为每类值所占百分比
tabulate(x)
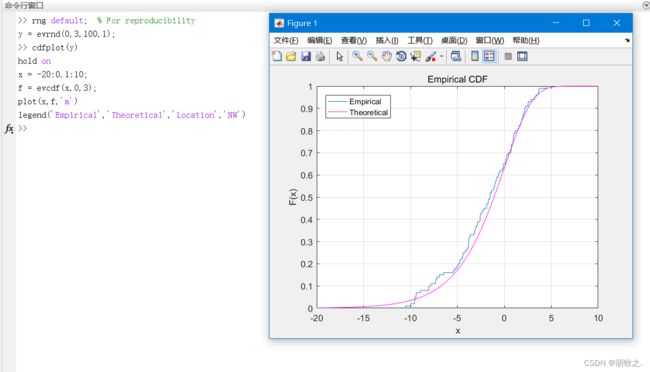
(二)累积分布函数图形 cdfplot
其具体用法如下
cdfplot(X) X为向量,F(X)的定义就是值小于等于X的元素的个数占比
h = cdfplot(X) 返回cdf曲线的句柄
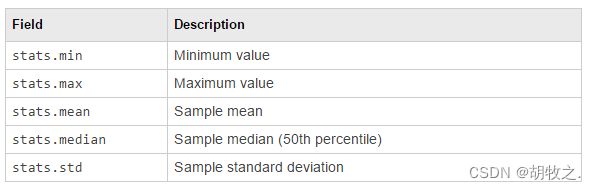
[h,stats] = cdfplot(X) stats为一个结构体,包含了一些样本的特征
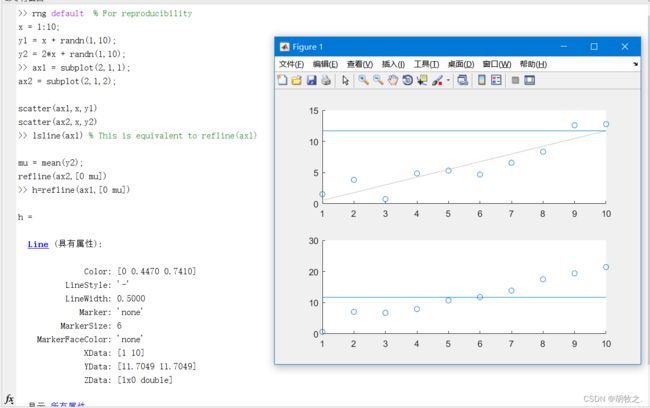
(三)最小二乘拟合直线 lsline
Least-squares line
其具体用法如下
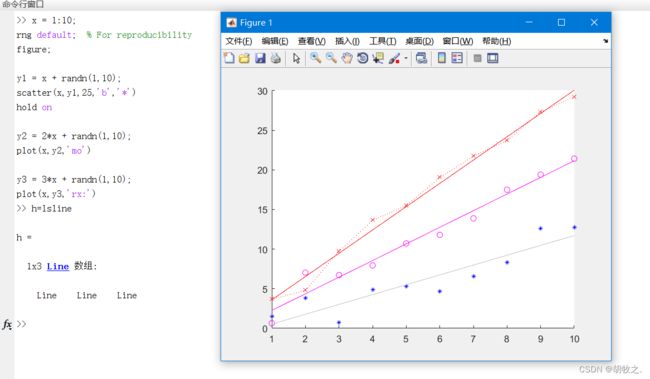
lsline 为当前轴上的散点图叠加最小二乘拟合直线;实线、虚线和点线图不会被视作散点图,会被忽略
lsline(ax) 在ax轴上处理
h = lsline(___) 返回由最小二乘线句柄组成的列向量
(四)绘制正态分布概率图形 normplot
正态概率图介绍
其具体用法如下
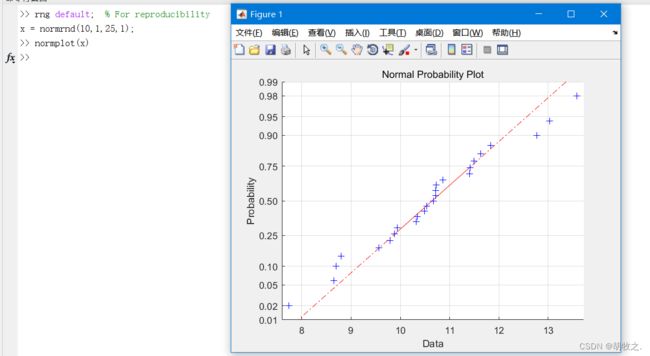
normplot(x) x就是待分析的数据,用于可视化检验正态性,当x是矩阵时,对每一列显示一条直线;
h=normplot(x)h返回由直线的句柄组成的列向量
正态概率图,其纵坐标为累积概率,是非等距刻度,横坐标为分位数或数值,为等距刻度
通过绘制抽样点在概率纸上的实际位置,观察其偏离直线的程度,就可以判断抽样数据是否符合正态分布了
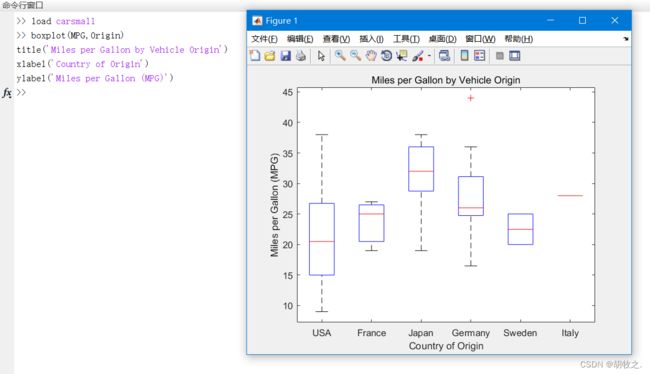
(五)样本数据的箱线图 boxplot
在箱线图中,箱子的中间有一条线,代表了数据的中位数。
箱子的上下底,分别是数据的上四分位数(Q3)和下四分位数(Q1),这意味着箱体包含了50%的数据。因此,箱子的高度在一定程度上反映了数据的波动程度。
上下边缘则代表了该组数据(不包含离群值)的最大值和最小值。
有时候箱子外部会有一些点,可以理解为数据中的“异常值”。
知乎——箱线图介绍
CSDN——boxplot用法
boxplot帮助文档
其具体用法如下
boxplot(x) 若x是矩阵,对每一列作箱线图
boxplot(x,g) g为分组变量,使用g中包含的一个或多个分组变量创建箱线图,boxplot为具有相同的一个或多个g值的各组x值创建一个单独的箱子
boxplot(ax,___) 在ax指定的坐标轴上作图
boxplot(___,Name,Value) 使用由一个或多个Name,Value对组参数指定的附加选项创建箱线图,例如指定箱子样式或顺序
(六)参考线绘制 refline / refcurve
绘制参考线
在 M A T L A B MATLAB MATLAB中可以使用 r e f l i n e refline refline和 r e f c u r v e refcurve refcurve函数分别绘制一条参考直线与一条参考曲线
1.refline——叠加参考直线
refline帮助文档
其具体用法如下
refline(m,b) m为斜率,b为截距
refline(coeffs) coeffs是一个双元系数向量,向图中添加直线:y=coeffs(1)*x+coeffs(2)
refline 没有输入参数时就相当于最小二乘拟合lsline
refline(ax,___) 在ax指定坐标区的图上添加一条参考线
hline = refline(___) 使用上述任一语法中的输入参数,返回参考线对象 hline。在创建参考线后,使用 hline 修改其属性
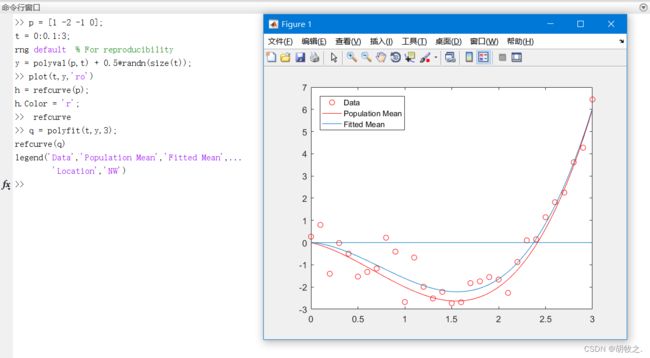
2.refcurve——叠加参考曲线
refcurve帮助文档
其具体用法如下
refcurve(p) 将系数为p的多项式参考曲线添加到当前轴,p为向量
refcurve 在没有输入参数的前提下,沿着x轴作一条直线
refcurve(ax,p) 使用在axes(一个Axes对象)中指定的绘图轴
hcurve = refcurve(...) 用法同refline
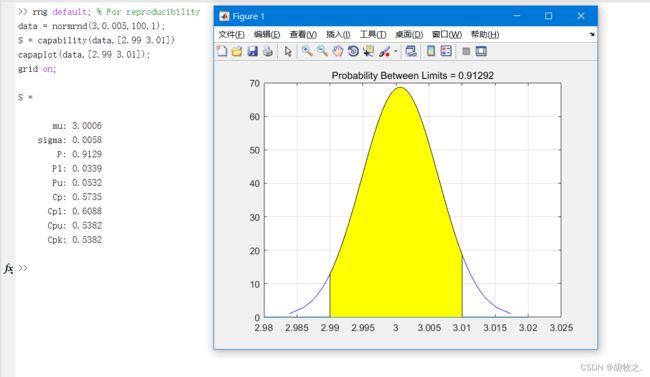
(七)样本概率图形 capaplot / capability
样本概率图形绘制函数capaplot
其具体用法如下
p = capaplot(data,specs) data为数据向量,specs为双元素向量,表示一个范围;假定数据为正态分布
最终将返回p,表示数据落入specs所表示范围的概率;并绘制图像,将specs部分置为阴影
[p,h] = capaplot(data,specs) h由图像句柄元素所组成
capability函数:计算数据的均值和方差等
capability帮助文档

(八)正态拟合直方图 histfit
正态拟合直方图绘制函数histfit
其具体用法如下
histfit(data) data为向量,直方图中竖条区域(bin)个数为data中元素个数的平方根
histfit(data,nbins) 指定bin为nbins
histfit(data,nbins,dist) 根据dist来进行密度函数的拟合,默认为normal
h = histfit(___) 返回句柄向量 h,其中 h(1) 是直方图的句柄,h(2) 是密度曲线的句柄