Lesson 12.3 线性回归建模实验

Lesson 12.3 线性回归建模实验

一、深度学习建模流程

  数据准备就绪，接下来就是建模实验环节，在实际深度学习建模过程中，无论是手动实现还是调库实现，我们都需要遵循深度学习建模一般流程。在此前的学习过程中，我们曾两次提及深度学习建模流程，结合此前学习内容，我们先进行简单回顾。

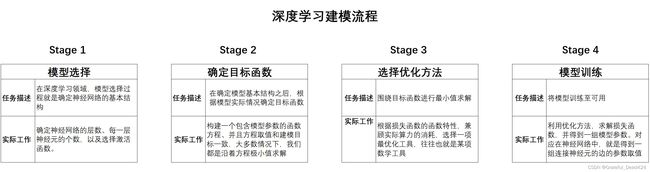
根据此流程，我们进行线性回归建模

二、线性回归的手动实现

  首先，考虑如何手动实现建模过程。

# 随机模块
import random

# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt

# numpy
import numpy as np

# pytorch
import torch
from torch import nn,optim
import torch.nn.functional as F
from torch.utils.data import Dataset,TensorDataset,DataLoader
from torch.utils.tensorboard import SummaryWriter

# 自定义模块
from torchLearning import *

1.生成数据集

  利用此前的数据集生成函数，创建一个真实关系为$y=2x_1-x_2+1$，且扰动项不是很大的回归类数据集。

tensorGenReg?
#Signature: tensorGenReg(num_examples=1000, w=[2, -1, 1], bias=True, delta=0.01, deg=1)
#Docstring:
#回归类数据集创建函数。
#
#:param num_examples: 创建数据集的数据量
#:param w: 特征系数矩阵
#:param bias：是否需要截距
#:param delta：扰动项取值
#:param deg：方程次数
#:return: 生成的特征张和标签张量
#File:      f:\code file\pytorch实战\torchlearning.py
#Type:      function
torch.manual_seed(420)   
features, labels = tensorGenReg()

2.建模流程

• Stage 1.模型选择

围绕建模目标，我们可以构建一个只包含一层的神经网络进行建模。

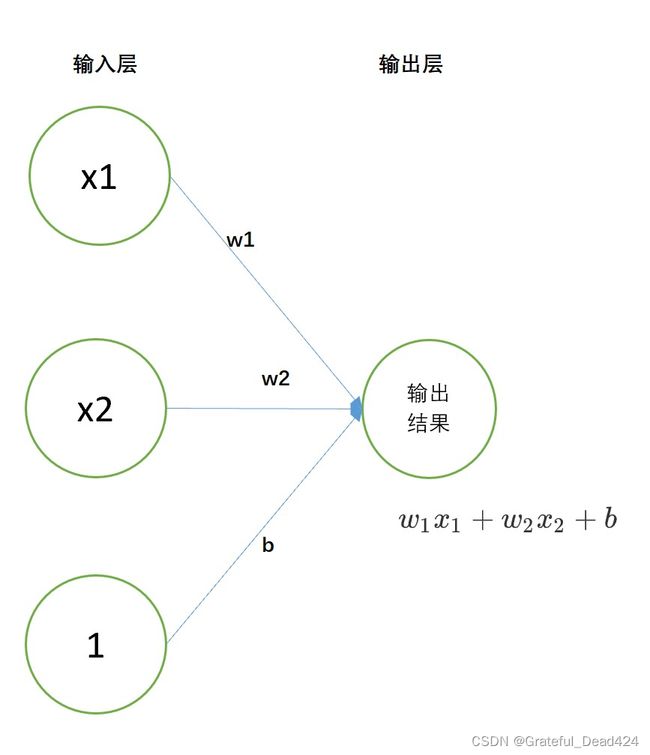
def linreg(X, w):
    return torch.mm(X, w)

• Stage 2.确定目标函数

和此前一样，我们使用MSE作为损失函数，也就是目标函数

def squared_loss(y_hat, y):
    num_ = y.numel()
    sse = torch.sum((y_hat.reshape(-1, 1) - y.reshape(-1, 1)) ** 2)
    return sse / num_

• Stage 3.定义优化算法

此处我们采用小批量梯度下降进行求解，每一次迭代过程都是(参数-学习率*梯度)。

def sgd(params, lr):
    params.data -= lr * params.grad 
    params.grad.zero_()

关于可微张量的in-place operation（对原对像修改操作）的相关讨论

(1).正常情况下，可微张量的in-place operation会导致系统无法区分叶节点和其他节点的问题

w = torch.tensor(2., requires_grad = True)
w
#tensor(2., requires_grad=True)
w.is_leaf
#True

开启可微之后，w的所有计算都会被纳入计算图中

w1 = w * 2
w1
#tensor(4., grad_fn=)

但如果在计算过程中，我们使用in-place operation，让新生成的值替换w原始值，则会报错

w = torch.tensor(2., requires_grad = True)
w -= w * 2
#RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.

从报错信息中可知，PyTorch中不允许叶节点使用in-place operation，根本原因是会造成叶节点和其他节点类型混乱。不过，虽然可微张量不允许in-place operation，但却可以通过其他方法进行对w进行修改。

w = torch.tensor(2., requires_grad = True)
w = w * 2

不过此时，w就不再是叶节点了

w
#tensor(4., grad_fn=)
w.is_leaf
#False

自然，我们也无法通过反向传播求其导数

w = torch.tensor(2., requires_grad = True)
w = w * 2
w.backward()       # w已经成为输出节点
w.grad
#D:\Users\ASUS\anaconda3\lib\site-packages\ipykernel_launcher.py:1: UserWarning: The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the gradient for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more informations.
#  """Entry point for launching an IPython kernel.

而在一张计算图中，缺少了对叶节点反向传播求导数的相关运算，计算图也就失去了核心价值。因此在实际操作过程中，应该尽量避免导致叶节点丢失的相关操作。
(2).叶节点数值修改方法
  当然，如果出现了一定要修改叶节点的取值的情况，典型的如梯度下降过程中利用梯度值修改参数值时，可以使用此前介绍的暂停追踪的方法，如使用with torch.no_grad()语句或者torch.detach()方法，使得修改叶节点数值时暂停追踪，然后再生成新的叶节点带入计算，如：

w = torch.tensor(2., requires_grad = True)
w
#tensor(2., requires_grad=True)
# 利用with torch.no_grad()暂停追踪
with torch.no_grad():
    w -= w * 2
w
#tensor(-2., requires_grad=True)
w.is_leaf
#True
w = torch.tensor(2., requires_grad = True)
w
#tensor(2., requires_grad=True)
# 利用detach生成新变量
w.detach_()
#tensor(2.)
w -= w * 2
w
#tensor(-2.)
w.requires_grad = True
w
#tensor(-2., requires_grad=True)
w.is_leaf
#True

当然，此处我们介绍另一种方法，.data来返回可微张量的取值，从在避免在修改的过程中被追踪

w = torch.tensor(2., requires_grad = True)
w
#tensor(2., requires_grad=True)
w.data         # 查看张量的数值
#tensor(2.)
w              # 但不改变张量本身可微性
#tensor(2., requires_grad=True)
w.data -= w * 2  # 对其数值进行修改
w
#tensor(-2., requires_grad=True)
w.is_leaf       # 张量仍然是叶节点
#True

这里需要注意，在Lesson 6中我们曾使用手写梯度下降算法计算线性方程自变量权重，但该过程在修改变量时并未使用反向传播计算梯度，我们是通过矩阵运算算得的梯度，因此并未出现叶节点位置丢失的问题。当然，更加严谨的做法是令weight不可导。

• Stage.4 训练模型

# 设置随机数种子
torch.manual_seed(420)    

# 初始化核心参数
batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据
w = torch.zeros(3, 1, requires_grad = True)    # 随机设置初始权重

# 参与训练的模型方程
net = linreg                                   # 使用回归方程
loss = squared_loss                            # MSE作为损失函数

# 模型训练过程
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w), y)
        l.backward()
        sgd(w, lr) #反向传播梯度就已经保存在w当中了
    train_l = loss(net(features, w), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l))
#epoch 1, loss 0.000122
#epoch 2, loss 0.000102
#epoch 3, loss 0.000101
w
#tensor([[ 2.0001],
#        [-1.0002],
#        [ 1.0002]], requires_grad=True)

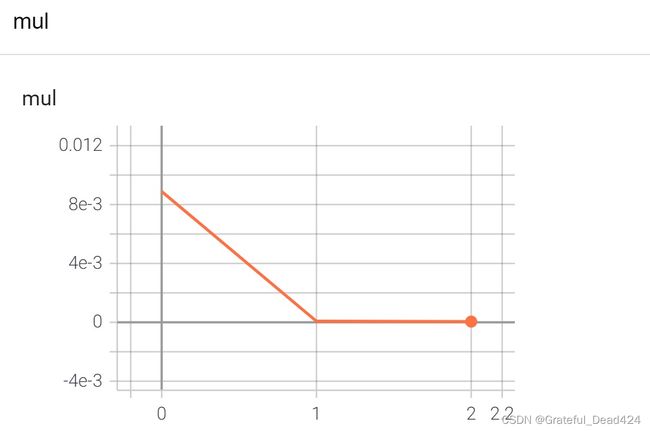
当然，我们也可以使用tensorboard记录上述迭代过程中loss的变化过程

writer = SummaryWriter(log_dir='reg_loss')

# 初始化核心参数
batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据
w = torch.zeros(3, 1, requires_grad = True)    # 随机设置初始权重

# 参与训练的模型方程
net = linreg                                   # 使用回归方程
loss = squared_loss                            # 均方误差的一半作为损失函数

# 模型训练过程
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w), y)
        l.backward()
        sgd(w, lr)
    train_l = loss(net(features, w), labels)
    writer.add_scalar('mul', train_l, epoch)

然后在命令行输入：

F:
cd "F:\Code File\PyTorch实战\"
tensorboard --logdir="reg_loss"

打开浏览器，输入localhost:6006，查看绘制图像

三、线性回归的快速实现

  当然，我们可以按照此前课程介绍的，通过调用PyTorch中的函数和类，直接完成建模。当然，该过程也是严格按照此前介绍的深度学习建模流程完成的模型构建，相关变量的符号也沿用了Lesson 11中的书写标准。
  不过，值得一提的是，由于深度学习的特殊性，深度学习的建模流程对于初学者来说并不简单，很多时候我们既无法对实际的数据进行表格式的查看，也无法精确的控制模型内部的每一步运行，外加需要创建大量的类（无论是读取数据还是建模），以及大规模的参数输入，都对初学者的学习造成了不小的麻烦。因此，通过接下来的调库建模练习，也希望学员能够进一步熟练掌握PyTorch框架的常用建模函数和类，从而为后续的学习打下良好的代码基础。

• 定义核心参数

batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据

• 数据准备

# 设置随机数种子
torch.manual_seed(420)   

# 创建数据集
features, labels = tensorGenReg()
features = features[:, :-1]                                  # 剔除最后全是1的列
data = TensorDataset(features, labels)                       # 数据封装
batchData = DataLoader(data, batch_size = batch_size, shuffle = True)      # 数据加载

features
#tensor([[-0.0070,  0.5044],
#        [ 0.6704, -0.3829],
#        [ 0.0302,  0.3826],
#        ...,
#        [-0.9164, -0.6087],
#        [ 0.7815,  1.2865],
#        [ 1.4819,  1.1390]])

• Stage 1.定义模型

class LR(nn.Module):
    def __init__(self, in_features=2, out_features=1):       # 定义模型的点线结构
        super(LR, self).__init__()
        self.linear = nn.Linear(in_features, out_features)
        
    def forward(self, x):                                    # 定义模型的正向传播规则
        out = self.linear(x)             
        return out

# 实例化模型
LR_model = LR()

• Stage 2.定义损失函数

criterion = nn.MSELoss()

• Stage 3.定义优化方法

optimizer = optim.SGD(LR_model.parameters(), lr = 0.03)

• Stage 4.模型训练

def fit(net, criterion, optimizer, batchdata, epochs):
    for epoch in range(epochs):
        for X, y in batchdata:
            yhat = net.forward(X)
            loss = criterion(yhat, y)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
        writer.add_scalar('loss', loss, global_step=epoch)     

当然，由于上述模型只有一层，因此也可以通过nn.Linear(2, 1)函数直接建模。

接下来，即可执行模型训练

# 设置随机数种子
torch.manual_seed(420)   

fit(net = LR_model, 
    criterion = criterion, 
    optimizer = optimizer, 
    batchdata = batchData, 
    epochs = num_epochs)

查看模型训练结果

LR_model
#LR(
#  (linear): Linear(in_features=2, out_features=1, bias=True)
#)
# 查看模型参数
list(LR_model.parameters())
#[Parameter containing:
# tensor([[ 1.9992, -1.0003]], requires_grad=True),
# Parameter containing:
# tensor([0.9994], requires_grad=True)]
# 计算MSE
criterion(LR_model(features), labels)
#tensor(0.0001, grad_fn=)

由于数据本身就是按照$y=2x_1-x_2+1$基本规律加上扰动项构建的，因此通过训练完成的参数可以看出模型效果较好。当然，真实场景下我们无法从上帝视角获得真实的数据分布规律，然后通过比对模型来判断模型好坏，此时我们就需要明确模型评估指标，相关内容我们将在下一节课详细介绍。

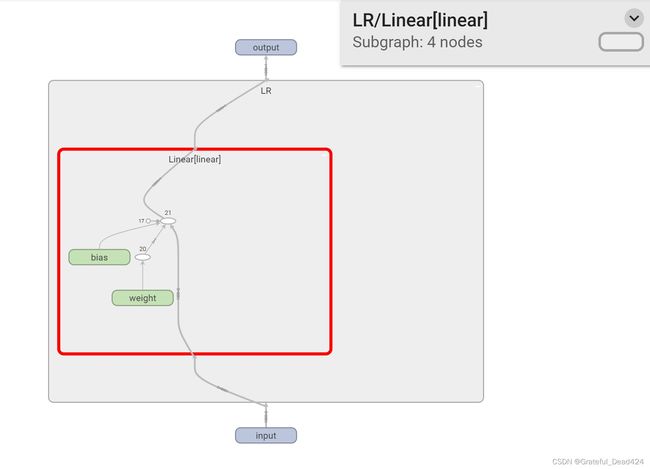
当然，我们也可以通过add_graph方法，在writer中添加上述模型的记录图

writer.add_graph(LR_model, (features,))

在graph一栏中能看到如下结果

简单线性回归局限性

此处我们进一步进行简单实验，当自变量和因变量满足最高次方为2次方的多项式函数关系时，或者扰动项增加时，简单线性回归误差将迅速增大。

# 设置随机数种子
torch.manual_seed(420)   

# 创建数据集
features, labels = tensorGenReg(deg=2)
features = features[:, :-1]                                  # 剔除最后全是1的列
data = TensorDataset(features, labels)
batchData = DataLoader(data, batch_size = batch_size, shuffle = True)

# 模型实例化
LR_model = LR()

# 定义优化算法
optimizer = optim.SGD(LR_model.parameters(), lr = 0.03)

# 模型训练
fit(net = LR_model, 
    criterion = criterion, 
    optimizer = optimizer, 
    batchdata = batchData, 
    epochs = num_epochs)

# MSE结果查看
criterion(LR_model(features), labels)
#tensor(10.1555, grad_fn=)
# 设置随机数种子
torch.manual_seed(420)   

# 创建数据集
features, labels = tensorGenReg(delta=2)
features = features[:, :-1]                                  # 剔除最后全是1的列
data = TensorDataset(features, labels)
batchData = DataLoader(data, batch_size = batch_size, shuffle = True)

# 模型实例化
LR_model = LR()

# 定义优化算法
optimizer = optim.SGD(LR_model.parameters(), lr = 0.03)

# 模型训练
fit(net = LR_model, 
    criterion = criterion, 
    optimizer = optimizer, 
    batchdata = batchData, 
    epochs = num_epochs)

# MSE结果查看
criterion(LR_model(features), labels)
#tensor(4.0763, grad_fn=)