机器学习（十五）异常检测

---

Log

2022.03.10开始第十五章的学习，先开个头，看样子肯定还要花不少时间。咱家这两天成中高风险区了，不出意外的话以后要待在宿舍上网课了。
2022.03.11把书本从研究院搬到了宿舍上课，继续学习
2022.03.12公寓封了。。。继续学习
2022.03.14真的是有些无语，事情多到不休息都做不完，现在这才先放下一些活回来学一下
2022.03.22继续学习
2022.03.23继续学习
2022.03.24继续学习
2022.03.25继续学习
2022.04.04最近好忙呀，但是我知道这并不是极限，还是要静下心来，认真把事情做好，少休息一会，多学一些，不亏
2022.04.06挤点时间，能学一会是一会
2022.04.24天天写实验报告都写麻了，十几份是有了，每份都不少写
2022.05.03五一假期，准备考试复习累了来写一会
2022.05.05时间大概是不够用了，这种笔记记法很费时，后面的内容会以简洁为主（配图会在文章发布后逐渐重新制作并替换）
2022.06.21考完试了，有时间了！学！
2022.06.22继续学习
2022.07.07继续学习
2022.07.17事情还是好多，晚上睡觉前学一会这个
2022.07.24继续学习，争取四天之内弄完
2022.07.25继续学习
2022.07.26继续学习
2022.07.27继续学习
2022.07.28结束这一章！

---

• 本篇文章主要介绍异常检测（anomaly detection） 问题。异常检测是机器学习算法的一个常见应用，这种算法的一个有趣之处在于，它虽然主要用在非监督学习问题，但是从某些角度看跟有监督学习问题是非常相似的。

一、问题动机（Problem motivation）

1. 直观理解异常检测

• 那么什么是异常检测，为了理解这个概念，先举一个例子：
  $$\begin{array}{rl}& Aircraftenginefeatures:\\ & x_1=heatgenerated\\ & x_2=vibrationintensity\\ & ...\\ & Dataset:\{x^{(1)},x^{(2)},...,x^{(m)}\}\\ & Newengine:x_{test}\end{array}$$

• 假如你是个飞机引擎制造商，当在生产线上生产飞机引擎时，需要进行质量控制测试，而作为这个测试的一部分，测试了飞机引擎的一些特征变量，比如测量了引擎运转时产生的热量，或者引擎的震动等等。在实际工作中，我们确实会从真实的飞机引擎采集这些特征变量，于是就有了一个数据集，从 x⁽¹⁾ 到 x^(m)，如果我们生产了 m 个引擎的话，可以将数据对应地画成图（下图左）：
  

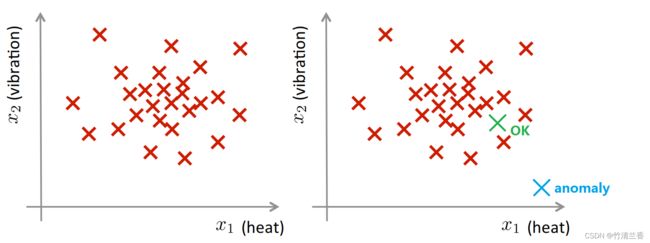
• 其中每个叉都是无标签数据，这样，异常检测问题可以定义如下：

• 假设后来有一天，有一个新的飞机引擎从生产线上生产出来，而你的新飞机引擎有一个特征变量集 x_test，所谓的异常检测问题就是我们希望知道这个新的飞机引擎是否有某种异常，或者说，我们希望判断这个引擎是否需要进一步测试，因为如果它看起来像一个正常的引擎，那么可以直接送出去，而不需要进一步的测试。比如说，如果新的引擎对应的点落在这里（上图右绿色样本），那么可以认为它看起来像是之前见过的引擎，因此可以直接认为它是正常的；然而，如果新飞机引擎对应点在外面（上图右蓝色样本），那么可以认为这是一个异常，也许需要在发货之前做进一步检测，这个引擎和之前见过的其它飞机引擎看起来不一样。

2. 正式定义异常检测

• 下面是更正式的定义异常检测问题：
  $$\begin{array}{rl}& \text{Density estimation:}\\ & \\ & Dataset:\{x^{(1)},x^{(2)},...,x^{(m)}\}\\ & Is{x}_{text}anomalous?\\ & Modelp(x)\\ & x_{test}\{\begin{array}{l}p(x_{test})<ϵ⟶flaganormaly\\ p(x_{test})\ge ϵ⟶OK\end{array}\end{array}$$

• 有一些数据，从 x⁽¹⁾ 到 x^(m)，我们通常假定这 m 个样本都是正常的（或者说都不是异常的），然后我们需要一个算法检测一个新的样本数据 x_test 是否是异常，我们要采取的方法是，给定无标签的训练集，我们将对数据建模，即 p(x)，也就是说，我们将对 x 的分布概率建模，其中 x 是飞机引擎的一系列特征变量。因此，当我们建立了 x 的概率模型之后，如果对于新的飞机引擎，也就是 x_test 的概率 p 低于阈值 ε，那么我们就将其标记为异常。

• 因此，当看到一个新的引擎，在根据训练数据得到的 p(x) 模型中，这个点出现的概率非常低时，我们就将其标记为异常；反之，如果 x_test 的概率 p 大于等于给定的阈值 ε，我们就认为是正常的。
  

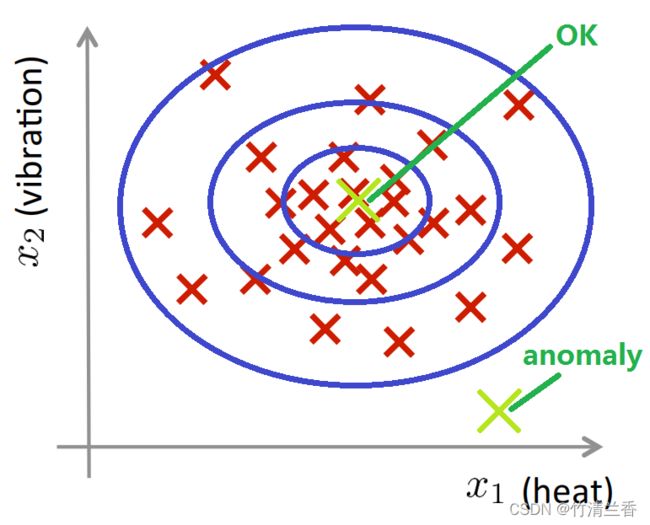
• 给定图中这样的训练集，如果你建立了一个模型，你将很可能发现飞机引擎对应的模型 p(x) 将会认为在中心区域的这些点概率相当大，这些点将是正常的，而稍微远离中心区域的点概率会小一些，更远的地方的点，它们的概率将更小，这些外面的点将成为异常点。

3. 异常检测应用案例

• 异常检测算法有下面这些应用案例：

①欺诈检测

$$\begin{array}{rl}& \text{Fraud detection:}\\ & x^{(i)}=featuresofuseri{}^{\prime }sactivities\\ & Modelp(x)fromdata\\ & Identifyunusualusersbycheckingwhichhavep(x)<ϵ\end{array}$$

• 异常检测最常见的应用也许就是欺诈检测。假设你有很多用户，你的每个用户都在从事不同的活动，也许是在你的网站上，也许是在一个实体工厂之类的地方。
• 你可以对不同的用户活动计算特征变量 x⁽ⁱ⁾，于是你可以建立一个模型来表示用户表现出各种行为的可能性，用来表示用户行为对应的特征向量出现的概率。因此，你可以看到某个用户在网站上的行为的特征变量是这样的，也许 x₁ 是用户登陆的频率， x₂ 是用户访问某个页面的次数或是交易的次数， x₃ 是用户在论坛上发帖的次数， x₄ 是用户的打字速度（有些网站是可以记录用户每秒打了多少个字母的）。
• 因此你可以根据这些数据建一个模型 p(x)，最后你将得到你的模型 p(x)，然后你可以用它来发现网站上的行为奇怪的用户，你只需要看哪些用户的 p(x) 概率小于 ε。
• 接下来你可以拿这些用户档案做进一步筛选，或者要求这些用户验证他们的身份，从而让你的网站防御异常行为或者欺诈行为（fraudulent behavior）。这样的技术将会找到行为不寻常的用户，而不只是有欺诈行为的用户，也不只是那些被盗号的用户或者有奇怪行为的用户，而是行为不寻常的用户。但实际上这就是许多在线购物网站常用来识别异常用户的技术，这些用户行为奇怪可能是表示他们有欺诈行为或者是被盗号。

②工业生产领域

$$\begin{array}{r}\text{Manufacturing}\end{array}$$

• 异常检测的另一个例子是在工业生产领域。事实上，之前已经谈到过飞机引擎的问题，你可以找到异常的飞机引擎，然后要求进一步细查这些引擎的质量。

③数据中心的计算机监控

$$\begin{array}{rl}& \text{Monitoring computers in a data center:}\\ & x^{(i)}=featuresofmachinei\\ & x_1=memoryuse\\ & x_2=numberofdiskaccesses/sec\\ & x_3=CPUload\\ & x_4=CPUload/networktraffic\\ & ...\end{array}$$

• 第三个应用是数据中心的计算机监控。如果你管理一个计算机集群或者一个数据中心，其中有许多计算机，那么我们可以为每台计算机计算特征变量，也许某些特征衡量计算机的内存消耗或者硬盘访问量、CPU 负载，或者一些更加复杂的特性，例如一台计算机的 CPU 负载与网络流量的比值。
• 那么，给定正常情况下，数据中心的计算机的特征变量，你可以可以建立 p(x) 模型，也就是说你可以建模这些计算机出现不同内存消耗的概率，或者出现不同硬盘访问量的概率，或者不同的 CPU 负载等等。然后如果有一台计算机，它的 p(x) 非常小，那么你可以认为这个计算机运行不正常，或许它即将停机，因此你可以让系统管理员查看其工作状况。目前，这种技术实际正在被各大数据中心用来监测大量计算机可能发生的异常。

二、高斯分布（Gaussian distribution）

• 这节主要介绍高斯分布（Gaussian distribution），也称为正态分布（normal distribution）。

1. 数学基础

• 假设 x 是一个实数的随机变量，如果 x 的概率分布服从高斯分布，其中均值为 μ，方差为 σ 的平方，那么将它记作：
  $$\begin{array}{r}x\sim N(\mu ,{\sigma }^2)\end{array}$$

• 其中的波浪号叫做什么的分布（distributed as），为了表示高斯分布，有时用大写字母 N 来表示（也就是正态分布，二者是同义词）。如果我们将高斯分布的概率密度函数绘制出来，它看起来将是这样一个钟形的曲线（下图），它由两个参数控制，分别是 μ 和 σ ，其中 μ 控制这个钟形曲线的中心位置， σ 控制这个钟形曲线的宽度，因此参数 σ 有时也称作一个标准差（one standard deviation）。
  

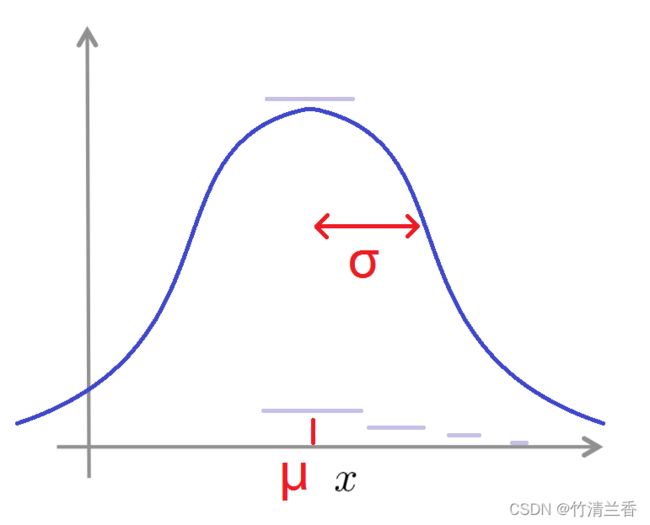
• 这条钟形曲线决定了 x 取不同值的概率，因此 x 取中间这些值的时候输出的概率相当大，因为高斯分布的概率密度在中间位置很大，而 x 取远处和更远处的值时，概率将逐渐降低直至消失。

• 最后为了讲述的完整性，下面给出高斯分布的数学公式：
  $$\begin{array}{r}p(x;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }exp\left(-\frac{(x-\mu {)}^2}{2{\sigma }^2}\right)\end{array}$$

2. 具体实例

• 下面给出几个在 μ 和 σ 取不同的值时对应的图像，以更好地理解高斯分布以及 μ 和 σ 取值变化对函数取值产生的影响：
  
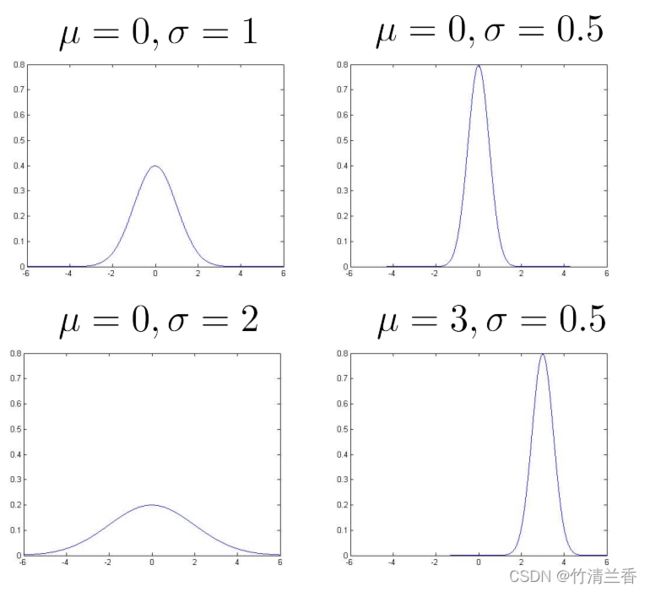
• 不难看出， 均值 μ 决定了中心位置，标准差 σ 大则图像矮而胖，小则图像窄而高，而无论图像如何变化，曲线下方的面积总等于 1（表示 x 各个取值对应的概率之和）。

3. 参数估计（Parameter estimation）

• 假设我们有一个数据集，其中有 m 个样本从 x⁽¹⁾ 到 x^(m) ，并且都是实数，分布在二维坐标系的横轴 x 轴上，我们可以用高斯分布来拟合这些样本，样本集中的地方代表出现的概率要高，越向外面概率就越小，下面是估计 μ 和 σ 两个参数的标准公式：
• μ 是对所有的样本取平均值
  $$\begin{array}{r}\mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)}\end{array}$$
• 标准差则是通过下面这个式子计算：
  $$\begin{array}{r}{\sigma }^2=\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu {)}^2\end{array}$$
• 这里的估计实际上是对 μ 和 σ 的平方的极大似然估计（the maximum likelihood estimates）。
  $$\begin{array}{r}{\sigma }^2=\frac{1}{m-1}\sum _{i=1}^m(x^{(i)}-\mu {)}^2\end{array}$$
• 在统计学中，上面计算 σ 的平方的公式里面的 m 也可以是 m-1 ，但是在机器学习领域中我们常用 m 的版本，虽然两个版本在理论特性和数学特性上稍有不同，但是在实践中二者的区别很小，只要我们有一个还算大的数据集，就都可以估计出一个很好地参数。

三、算法（Algorithm）

• 本小节我们将应用高斯分布来构建一个异常检测算法。

1. 密度估计（Density estimation）

• 假定我们有一个共有 m 个样本的无标签训练集，训练集里的每个样本都是一个 Rⁿ 维的特征量，因此我们的训练集可以是来自一个 m 的 m 个特征向量集合，比如飞机引擎成品的样本集，或者是来自m个用户或是别的。
  $$\begin{array}{rl}& \text{Training set : }\{x^{(1)},...x^{(m)}\}\\ & Eachexampleisx\in {\mathbb{R}}^n\end{array}$$
• 我们处理异常检测的方法是，我们要用数据集建立起概率模型 p(x)，我们要试图解决出哪些特征量出现的概率比较高，哪些特征量的出现概率比较低。因此，x 就会是个向量，然后我们就要建立模型 p(x) 作为 x₁ 的概率，这是 x 的第一个组成部分，并用它乘以 x₂ 的概率，这是第二个特征量的概率，再乘以第三个特征量的概率，等等，直到最后一个特征量 x_n:

$$\begin{array}{r}p(x)=p(x_1)p(x_2)p(x_3)...p(x_n)\end{array}$$

• 那么，如何对 p(x₁)、p(x₂) 等等这些项建模呢？假定特征 x₁ 是分散的，它服从高斯正态分布，它有某个期望，可以写为 μ₁，以及某个方差，用 σ₁² 表示。这样 p(x₁) 就可以写成这样一个高斯分布，N(μ₁, σ₁²)，同样，假设 x₂ 也服从高斯分布，一直到 x_n 也是如此。
  $$\begin{array}{rl}& x_1\sim N({\mu }_1,{\sigma }_1^2)\\ & x_2\sim N({\mu }_2,{\sigma }_2^2)\\ & x_3\sim N({\mu }_3,{\sigma }_3^2)\\ & ...\end{array}$$

• 进而我们就在原式的基础上进一步细化，得到了我们要说的模型（下式）。下面这个等式实际上等同于一个 x₁ 到 x_n 上的独立假设。不过在实践中，结果表明，我们将要介绍的这个算法它的效果还不错，无论这些特征量是否近乎独立，并且即使这个独立假设不成立，这个算法也能正常运行。最后，我们来将这个式子写成一个乘积的形式（更紧凑一些）。

$$\begin{array}{rl}& p(x)\\ =& p(x_1;{\mu }_1,{\sigma }_1^2)p(x_2;{\mu }_2,{\sigma }_2^2)p(x_3;{\mu }_3,{\sigma }_3^2)...p(x_n;{\mu }_n,{\sigma }_n^2)\\ =& \prod _{j=1}^{n}p(x_j;{\mu }_j,{\sigma }_j^2)\end{array}$$

• 这个分布项 p(x) 的估计问题，有时称作是密度估计问题（the problem of density estimation）。

2. 异常检测算法

• 整理一下，这就是我们的异常检测算法：
  $$\begin{array}{rl}\text{1.}& Choosefeatures{x}_{i}thatyouthinkmightbeindicativeof\\ & anomalousexamples.\\ \text{2.}& Fitparameters{\mu }_1,...,{\mu }_n,{\sigma }_1^2,...,{\sigma }_n^2\\ & {\mu }_j=\frac{1}{m}\sum _{i=1}^m{x}_j^{(i)}\\ & {\sigma }_j^2=\frac{1}{m}\sum _{i=1}^m(x_j^{(i)}-{\mu }_j{)}^2\\ \text{3.}& Givennewexamplex,computep(x):\\ & p(x)=\prod _{j=1}^{n}p(x_j;{\mu }_j,{\sigma }_j^2)=\prod _{j=1}^n\frac{1}{\sqrt{2\pi }{\sigma }_j}exp\left(-\frac{(x_j-{\mu }_j{)}^2}{2{\sigma }_j^2}\right)\\ & Anomalyifp(x)<ϵ\end{array}$$

1. 第一步是选择特征量，或是想出一些特征量 x_j，它能够帮助我们指出那些反常的样本，即尝试提出一些特征，这样当有一个反常用户在你的系统中做一些不正当行为时，或对于飞机引擎的例子，当飞机引擎出现了一些奇怪的问题时，选择这样的特征 x_j，当出现异常样本时，特征值会异常地特别大，或者异常地特别小，但通常来说，还是选择那些能够描述你所想的能够描述你所收集的数据的一般特性的特征。
2. 第二步是在给出训练集（就是 m 个未做标记的样本，从 x⁽¹⁾ 到 x^(m)）之后，进行参数拟合，μ₁ 到 μ_n，δ₁² 到 δ_n²，同时这些公式和之前章节里的公式比较相似，因此我们便可以估计这些参数的值。
   再稍微解释一下，μ_j 就是特征量 j 的平均值，因此，对于 μ_j，就取训练集中特征 j 的平均值即可，对于 j = 1到 n 可以用上面的这些公式来估计 μ₁，再估计 μ₂，直到 μ_n。
   同样地，对于 δ²，也是能够得出这些参数的向量化的参数特征，如果我们把 μ 假想成一个向量，那么向量 μ 就是 μ₁、 μ₂ 到 μ_n，那么那些参数集的向量化特征就能被写作下面这样的：
   $$\begin{array}{r}\mu =\left[\begin{array}{c}{\mu }_1\\ {\mu }_2\\ ...\\ {\mu }_n\end{array}\right]=\frac{1}{m}\sum _{i=1}^m{x}^{(i)}\end{array}$$
   对 x⁽ⁱ⁾ 的值从 1 到 n 进行求和，因此上面的的这个公式就用 x_i 值估计出了 μ 的特征向量，同时估计出所有的 n 个 μ 值；除此之外我们还可以得出一个向量化公式用来估计 δ^j 。
3. 最后，我们给出一个新案例，当有一个全新的飞机引擎时，如果我们想知道这个飞机引擎是否异常，那么我们要做的就是计算 p(x) 的值，这个案例的出错概率是多少呢？p(x) 的值就等于这个累乘项（上面第三步中的公式），并且要计算的就是后面具体的公式，其中每一个累乘项都是一个计算高斯概率的公式，如果计算出的这个概率值很小，那么就将这一项标注为异常，下一节是应用这种方法的一个案例。

3. 异常检测实例

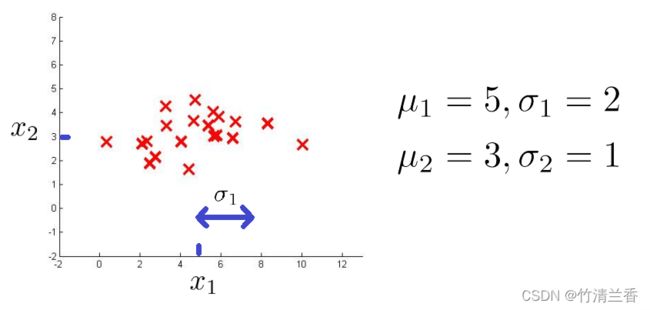
• 假定我们有如下数据集，看一下特征量 x₁ 以及这个数据集，它看起来比较平均， x₁ 特征量中均值为 5，并且有标准差。如果我们只看数据集中的 x₁ 方向的数值，其标准差可能为 2，也就是 σ₁ ；对应地，纵轴所测量的特征值 x₂ ，它的平均值可能是 3，并且标准差的值为 1 。如果用这个数据集来估计 μ₁ 、μ ₂ 、σ₁ 、σ₂ ，这些就是我们可以得到的。
  

• p( x₁; μ₁, σ₁² ) 和 p( x₂; μ₂, σ₂² ) ，它们看起来像是下图的两个分布。
  

• 实际上，如果绘制出 p(x) 的图像的话，也就是上面两个方向上的 p(x) 的乘积，我们会得到一个类似于下图的曲面图，这就是 p(x) 的图示，它的高度就是它所落在的曲面上那一点的高度，也就是说，给定一个特定的 x₁ 和 x₂ 的值，在曲面中对应点的高度的数值就是 p(x₁) 乘以 p(x₂)。
  

• 现在我们就得出了如何对这些数据拟合出参数值，再来看一些新的案例，假定在数据集中有两个新例子（下图绿色样本），那么这两个例子是否异常呢？处理这个问题的方法是，对 ε 设置某个值，假如选定 ε = 0.02（之后会讲到如何选取ε的值）。
  

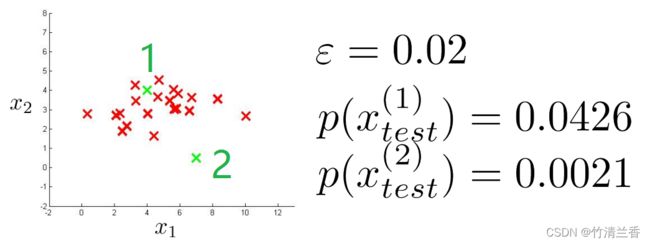
• 先讲第一个例子，称作是 x⁽¹⁾_test，同时第二个例子称作是 x⁽²⁾_test，接下来我们计算出 p(x⁽¹⁾_test)，用这个公式来进行计算：
  $$\begin{array}{r}p(x)=p(x_1;{\mu }_1,{\sigma }_1^2)p(x_2;{\mu }_2,{\sigma }_2^2)\end{array}$$

• 不难发现这是一个相当大的数，特别地，这个值可能大于等于 ε，因此这是个相当大的概率，至少比 ε 大，因此我们就说 x⁽¹⁾_test 没有异常；然而，如果计算 x⁽²⁾_test 的值，它会是一个更加小的值（比 ε 小），因此说它确实出现了异常，因为它比选定的 ε 值小很多。
  

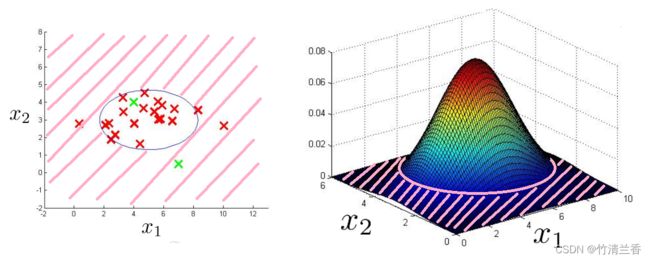
• 事实上，我们可以改良这个方法，从这个三维曲面图可以看出所有的 x₁ 和 x₂ 值，所在位置都是比较高的点对应的就是无异常情况，或者说是一个正常例子；相反，所有那些更远的点的概率值都相当小，所以我们会将这些点标注为异常。因此，我们可以定义某个范围，在这之外的（上图左粉色阴影区域）都会标注为异常，对于上面我们给出的例子，x⁽¹⁾ 是非异常的，而 x⁽²⁾ 是异常的。

四、开发和评估异常检测系统（Developing and evaluating an anomaly detection system）

• 本节将介绍如何开发一个异常检测的应用来解决实际问题，我们将重点关注如何评估一个异常检测算法。

1. 实数评估的重要性（the importance of real-number evaluation）

• 在之前的内容中，我们已经介绍了实数评估的重要性，它的主要思想是，当你为某个应用开发一个学习算法时，你需要进行一系列的选择，比如选择使用什么特征等等，如果你有某种方法，通过返回一个实数来评估你的算法，那么对这些选择作出决定往往会容易得多。

• 比如你需要决定该不该把想到的一个额外的特征纳入当前的特征中，如果你分别在纳入该特征和不纳入该特征情况下运行算法，然后算法返回一个数字，来告诉你这个特征对算法的影响是好是坏，这样的话，你就能更简单地决定要不要纳入这个特征。

• 有一个方法来评估异常检测系统（anomaly detection system） 对于快速地开发出这样一个系统是非常有帮助的。为了实现这一点（评估一个异常检测系统），假如有一些带标签的数据，到目前为止，我们都把异常检测看作是一个无监督学习问题（因为用的是无标签的数据），但是如果你有一些带标签的数据，来指明哪些是异常样本，哪些是正常样本，这也就是我们认为的可以评估异常检测算法的标准方法。

• 还是用飞机引擎的例子，假如有一些带标签的数据代表异常样本，代表这批引擎是异常的；同时还有一些无异常的样本。用 y = 0 来表示这些无异常或者正常的样本，用 y = 1 来代表异常样本。
  那么异常检测算法的开发过程以及评估算法如下所示：
  $$\begin{array}{rl}& \text{Training set:}{x}^{(1)},x^{(2)},...,x^{(m)}(assumenormalexamples/notanomalous)\\ & \text{Cross validation set:}(x_{cv}^{(1)},y_{cv}^{(1)}),...,(x_{cv}^{(m_{cv})},y_{cv}^{(m_{cv})})\\ & \text{Test set:}(x_{test}^{(1)},y_{test}^{(1)}),...,(x_{test}^{(m_{test})},y_{test}^{(m_{test})})\end{array}$$

• 我们先假设有一训练集，并把该训练集看作是无标签的，所以它是一个很大的正常样本（或无异常样本）的集合。通常来说，把它们看作是无异常样本，即使溜进了一些异常样本也没关系。接下来我们要定义一个交叉验证集和测试集，用来评估这个异常检测算法。具体来说，对交叉验证集和测试集，假设在交叉验证集和测试集中，包含一些已知是异常的样本，所以在测试集中，有一些标签是 y = 1 的样本（代表异常的飞机引擎）。

• 举一个具体的例子，数据集如下：
  $$\begin{array}{rl}& \text{Aircraft rngines motivating example}\\ & 10000good(normal)engines\\ & 20flawedengines(anomalous)\end{array}$$

• 所有数据如下：制造了10000个引擎来作为样本（正常的完好的飞机引擎），并且，即使有一些异常的引擎混入了这10000个样本也没有关系。

• 假设这10000个样本绝大多数都是正常的引擎，其中包含20个异常引擎。对于典型的异常检测应用来说，异常样本的数量，也就是这些 y = 1 的样本，大概是20到50个，这是一个很常见的 y = 1 样本数量的范围，而且通常来说，正样本的数量还要大得多。

• 有了这组数据，我们要把数据分离到训练集、交叉验证集和测试集，一种典型的方法如下：
  $$\begin{array}{rl}& Trainingset:6000goodengines\\ & CV:2000goodengines(y=0),10anomalous(y=1)\\ & Test:2000goodengines(y=0),10anomalous(y=1)\end{array}$$

• 把这 10000 个正常引擎其中 6000 个放到无标签训练集中（虽然我们把它叫做无标签数据集，但实际上这些样本都对应标签 y = 0），我们要用它们来拟合p(x)：
  $$\begin{array}{rl}& p(x)=p(x_1;{\mu }_1;{\sigma }_1^2)...p(x_n;{\mu }_n;{\sigma }_n^2)\end{array}$$

• 用这6000个样本来评估参数 μ₁, σ₁²,…, μ_n, σ_n²，这些就是正常或者说大多数正常的样本所在的训练集。然后把剩下的正常的引擎中的一些放到交叉验证集中，再放一些到测试集中。我们还有 20 个异常的飞机引擎，也把它们进行分离，其中 10 个放到交叉验证集中，10 个放到测试集中。

• 上面用到的是比较推荐的划分带标签和无标签的数据的方法，即采用 6：2：2 的比例来分配正常样本，而对于异常样本，我们只把它们放在交叉验证集和测试集中。之后将说明这样分的理由。

• 但是在应用异常检测算法时，也存在着不恰当的划分方法：
  $$\begin{array}{rl}& Alternative:\\ & Trainingset:6000goodengines\\ & CV:4000goodengines(y=0),10anomalous(y=1)\\ & Test:4000goodengines(y=0),10anomalous(y=1)\end{array}$$

• 把10000个正常引擎中的 6000 个放在训练集中，然后把剩下的 4000 个样本同时用作交叉验证集和测试集。

• 我们通常认为，交叉验证集和测试集是两个完全不同的数据集，但在异常检测中，有时可能会看到别人把一部分正常的引擎同时用作交叉验证集和测试集，有时还可能看到别人把异常飞机引擎也同时用于交叉验证集和测试集。总之，所有这样的想法都是不太好的做法，也是很不推荐的做法，把同样的数据同时用于交叉验证集和测试集，这种方法在机器学习中是不好的做法。

2. 算法的推导和评估

• 得到训练集、交叉验证集和测试集之后，下面介绍如何推导和评估算法：
  $$\begin{array}{rl}& \text{Algorithm evaluation}\\ & Fitmodelp(x)ontrainingset\{x^{(1)},...,x^{(m)}\}\\ & Onacrossvalidation/testexamplex,predict\\ & y=\{\begin{array}{l}1ifp(x)<\epsilon (anomaly)\\ 0ifp(x)\ge \epsilon (normaly)\end{array}\end{array}$$

• 首先，使用训练集拟合模型 p(x)，也就是把这 m 个无标签样本都用高斯函数来拟合。虽然在这里把它们称作无标签样本，但实际上我们假设这些样本是正常的飞机引擎。

• 我们的异常检测算法实际上要进行预测，所以在交叉验证集和测试集中，假如有一个样本x，算法在 p(x) < ε 时，会预测 y = 1；而 p(x) ≥ ε 时，会预测 y = 0（即给出x的值，算法将预测出 y 的值，y = 1 对应异常样本，y = 0 对应正常样本）。

• 随后对于给定的训练集、交叉验证集和测试集，我们如何来推倒这个算法呢？更具体地说，应当如何来评估一个异常检测算法？

• 第一步是用无标签训练数据来拟合模型 p(x)（和前面一样，虽然说是无标签，但实际上我们假设这些样本绝大多数都是正常的飞机引擎），然后要拟合模型 p(x)，用高斯函数拟合这些参数。

• 接下来，对于交叉验证集和测试集，我们要让异常检测算法来预测 y 的值，于是对每一个测试样本，有 x^(i)_test 和 y^(i)_test，其中 y = 1 或 0 取决于该样本是否为正常样本，所以给定训练集中的x作为输入，异常检测算法将进行对应的预测：当 p(x) < ε 时，有 y = 1（当概率p很小的时候，会预测y=1），并且想要算法在 p(x) ≥ ε时，预测出 y = 0（也就是当p(x)很大的时候，会预测该样本为正常样本）。

• 所以现在我们可以把异常检测算法看成是对交叉验证集和测试集中的 y 标签进行预测，这和我们在监督学习中所做的非常相似，即我们的测试集是带标签的，而我们的算法要对这些标签作出预测，所以可以通过算法预测成功的次数来对算法进行评估。当然，这些标签会很倾斜，因为 y = 0 的情况，也就是正常的样本会比 y = 1 的异常样本常见得多。这跟在监督学习中用到的评价指标非常接近。

• 那么，什么是一个好的评价指标呢？
  $$\begin{array}{rl}& Possibleevaluationmetrics:\\ & -Truepositive,falsepositive,falsenegative,truenegative\\ & -Precition/Recall\\ & -F_1-score\\ & Canalsousecrossvalidationsettochooseparameterϵ\end{array}$$

• 因为我们的数据很倾斜（即 y = 0 的情况很常见），那么分类正确率就不是一个好的评价指标。在之前的文章中也介绍过，如果你有一个很倾斜的数据集，y = 0 的情况占了绝大多数，那么分类正确率就会一直都很高。

• 相比之下，如果我们用的是计算真阳性、假阳性、假阴性以及真阴性的比例，或者计算出算法的精度以及召回率，或者计算出像 F₁-score（它是一个实数），来总结和反映精度以及召回率。通过这些方法，就可以评估异常检测算法在交叉验证和测试集样本中的表现。

• 最后一点，之前在异常检测算法中，我们还有一个参数 ε，这个 ε 是我们用来决定什么时候把一个样本当作是异常样本的一个阈值。所以，如果你有一个交叉验证集，一个选择参数 ε 的方法就是尝试去使用许多不同的 ε 值，该 ε 值能够最大化 F₁-score 或者在其他方面有良好表现的 ε 值。

• 一般来说，使用训练集、交叉验证集和测试集的方法是：当进行决策时（比如决定要不要纳入某个特征，或者定义参数 ε 作为阈值），我们会在交叉验证集中评估算法，然后做出决策（例如用哪些特征，怎么设置 ε 值，用这个上面介绍的评价方法在交叉验证集中评估算法），当选择好特征，找到合适的 ε 值以后，我们就能用最后的模型来评估算法在测试集中对算法进行最后的评估。

五、异常检测与监督学习（Anomaly detection vs. supervised learning）

• 在上一节中，我们讨论了评估一个异常检测算法的过程，当时我们开始用了一些带有标签的数据，举了一些例子，这些例子要么正常要么异常，相应地我们用 y = 1 和 y = 0 标记，因此就出现了问题，假如我们有带标签的数据，如果我们有已知的是异常的例子，还有一些已知正常的例子，我们为什么不直接用一个监督学习算法？为什么我们不直接用逻辑回归或是神经网络算法来尝试直接学习我们带标签的数据，来预测 y 是否等于 1 或者 0 呢？
• 本节将分享一些思想和方法，当你使用异常检测算法时，能够用得上这些方法，并且在你使用监督学习算法时，这些方法可能会更有效。

1. 不同的使用情况

• 下表展示了什么情况下可能使用异常检测算法以及何时使用监督学习算法更有效：

Anomaly detection	Supervised learning
①Very small number of positive examples (y=1). (0-20 is common)	③Large number of positive and negative examples
②Large number of negative (y=0) examples
④Many different “types” of anomalies. Hard for any algorithm to learn from positive examples what the anomalies look like	⑥Enough positive examples for algorithm to get a sense of what positive examples are like, future positive examples likely to be similar to ones in training set
⑤future anomalies may look nothing like any of the anomalous examples we’ve seen so far

• ①如果你遇到了一个问题，它的正常例子数量很少（记住y=1时这些例子为异常样例），那么你可以考虑使用一个异常检测算法。典型情况下，我们有 0 到 20 个，可能最多到 50 个正样本，通常情况下，我们只有非常少量的正样本，接下来我们保存这些正样本用于交叉验证集和测试集。

• ②与此相反，在一个典型的异常检测中，我们经常会有一个比起正常样本（正常的航空发动机）数量更大的负样本，那么我们可以用这些庞大数量的负样本来拟合出 p(x) 的值，因此在许多异常检测应用中，有这样一个思想：如果有很少的正样本和很多的负样本，当我们在处理估计 p(x) 的值拟合所有的高斯参数的过程中，只需要负样本就够了。所以如果有大量的负样本，我们仍然可以很好的拟合 p(x) 的值。

• ③对于监督学习来说，更为典型的情况是在合理范围内会有大量的正样本和负样本，所以这是一种考虑问题的方式，来决定我们是应该使用一个异常检测算法还是一个监督学习算法。

• ④还有另一种人们经常考虑异常检测算法的方法，对于异常检测应用来说，经常有许多不同类型的异常，比如航空发动机，有很多不同途径导致发动机异常，也有许多部件可能出问题导致航空发动机宕机。因此，如果是这种情况，你有很少数量的正样本，那么对一个算法就很难去从小数量的正样本中去学习异常是什么。

• ⑤特别地，未来可能出现的异常看起来可能会与已有的截然不同，所以可能在正样本中，你可能已经了解 5 个或 10 个或 20 个航空发动机发生故障的情况，但是可能到了明天，你需要检测一个全新的集合、一种新类型异常、一种全新的飞机发动机出现故障的情况，而且之前从来就没有见过。如果是这样的情况，那么我们就更应该对负样本用高斯分布模型 p(x) 来建模，而不是费尽心思对正样本建模，因为明天的异常可能与迄今为止见过的情况完全不同。

• ⑥相反，在一些其它问题中，你有足够数量的正样本或是一个已经能识别正样本的算法，尤其是，假如你认为未来可能出现的正样本与你当前训练集中的正样本类似，那么这种情况下使用一个监督学习算法会更合理，它能够查看大量正样本和大量负样本来学到相应特征，并且能够尝试区分正样本和负样本。

• 总结： 当遇到一个特定问题时，我们应该能够判断出是用异常检测算法还是监督学习算法。二者的关键不同在于，在异常检测中，我们通常只有很少量的正样本，因此对于一个学习算法而言，它是不可能从这些正样本这学习到足够的知识的，所以我们要做的是使用大量负样本，让这个学习算法学到足够多的内容，从那些负样本中学习 p(x) 的值，比如说是飞机发动机故障的情况，我们保留小数量的正样本，用来评估我们的算法，这个算法用于交叉验证集或测试集。

• 顺便提一句，这些不同类型的异常，我们在之前的文章中曾讨论过垃圾邮件的例子，这些例子中，实际有许多不同类型的垃圾邮件，有些垃圾邮件企图向你兜售商品，有些企图偷取你的密码（钓鱼邮件），还有许多不同类型的垃圾邮件，但是对于垃圾邮件问题，通常有足够的垃圾邮件例子，垃圾邮件有许多不同类型，因为我们有大量垃圾邮件的例子，这就是为什么我们通常把垃圾邮件问题看成一个监督学习问题，即使有许多不同类型的垃圾邮件。

2. 不同的应用场合

Anomaly detection	Supervised learning
Fraud detection	Email spam classification
Manufacturing (e.g. aircraft engines)	Weather prediction (sunny/rainy/etc)
Monitoring machines in a data center	Cancer classification

• 相比于监督学习，观察一些异常检测的应用时，我们能够发现，在欺骗检测中如果你知道人们诈骗时的各种不同的类型，并有一个很小的训练集，对应少量有欺诈行为的用户，那么我们会用一个异常检测算法。假如说，如果你是一名大型的网络零售商，那么你的网站上肯定有很多人在进行欺诈行为，也就是说你有很多样本，这些样本的 y 等于 1，那么这个欺诈检测实际上可以转换成监督学习问题，但是如果你的网站上没那么多做坏事的用户样本，这时候更多的是把欺骗检测当作是异常检测算法来处理，而不是监督学习算法处理。
• 至于其它例子，已经讨论过的引擎制造，其中你能看到更多的正常样本，而没有那么多异常样本。但是话又说回来，对于一些生产过程，如果你在进行大规模生产，如果你见到了很多异常样本，那么生产问题也可以转为监督学习问题。但是如果并没有见到这么多异常样本，那么我们就会做异常检测。
• 在数据中心的机器监视例子中，也是相似的情况。
• 然而对于垃圾邮件的分类问题，天气预报问题以及癌症分类问题，如果你有相同量级的正样本和负样本，或者说同时有大量的正样本和负样本，那么我们会把这些情况都采用监督学习来处理。
• 总结： 通过以上的内容，我们应该明白学习算法的特征是什么，你是要将问题当成是异常检测算法来处理，还是监督学习算法去处理。这些问题许多科技公司都会面临，我们经常会遇到这种正样本的数量非常少的或者有各种类型的之前从未见过的异常样本，那么对于这种情况下，通常使用的算法是异常检测算法。

六、特征的选择（Choosing what features to use）

• 前面的章节中我们已经学习了异常检测算法，并且也讨论了如何评估一个异常检测算法。当应用异常检测时，其中有一个因素对运行有很大影响，那就是使用什么特征，或者说选择什么特征来实现异常检测算法。这一节将会给一些建议，关于如何设计或选择异常检测算法的特征。

1. 处理非高斯特征（Non-gaussian features）

• 在异常检测算法中，我们经常做的一件事是使用高斯分布来对特征建模，假设其函数 x_i 的期望是 μ_i ，方差是 σ_i²。
  $$\begin{array}{r}p(x_i;{\mu }_i,{\sigma }_i^2)\end{array}$$

• 我们经常做的一件事就是画出数据，或者用直方图表示数据，以确保这些数据在进入异常检测算法前，看上去比较接近于高斯分布。当然，这只是一种很好的卫生检查（sanitary check），即使我们数据并不是高斯分布，算法往往也能正常运行。但是，如果我们的数据画出来，看起来是像这样的直方图：
  

• 我们可以使用 Octave 中的 hist 指令画出上面的直方图，该图看上去近似于高斯分布，如果我们的特征是这样的话，那么我们将会很乐意将其输入到算法中，如果我们的数据直方图画出来是这样的（下图左），一点也不像一条钟形曲线，这是一个非常不均匀的分布，它的峰值分散在一边。如果数据是这样的话，我们通常会对数据进行一些不同的转换，使得它看上去更接近高斯分布，即使我们不这么做，算法也能运行，但如果我们使用这些转换，使数据更接近高斯分布，那么算法也许能运行的更好。
  

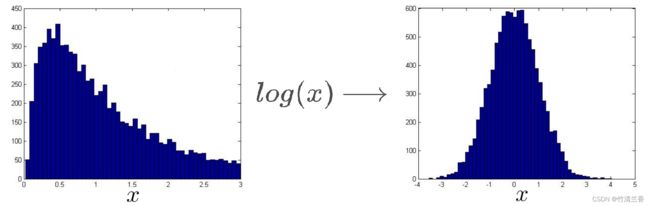
• 所以，假设所给的是这样的数据集，我们通常会对数据进行一次对数转换（log transformation），当我们这么做之后并重新画出直方图（上图右），在这个特殊的例子中，会得到一个像这样的直方图，这样看起来更像高斯分布了（典型的钟形曲线），这样我们就能拟合出期望和方差的参数了。

• 我们所说的进行对数转换的意思就是，如果有一些特征 x₁，并且 x₁的直方图是上图左那样的，那么可以将特征 x₁ 替换成 log(x₁)，这就会形成一个新的 x₁ ，将它的直方图画在右边，这看起来更像高斯分布了。
  $$\begin{array}{rl}& x_1⟵log(x_1)\\ & x_2⟵log(x_2+1)log(x_2+c)\\ & x_3⟵{\sqrt{x}}_3=x_3^{\frac{1}{2}}\\ & x_4⟵x_4^{\frac{1}{3}}\end{array}$$

• 除了取对数变换之外，还有别的一些方法也可以用，假设有一个不同的特征 x₂，现在我们用log(x₂+1)来取代 x₂ ，或者更一般地，用 log(x₂+c)，这个常数 c 可以任意调整，使得图形尽可能接近高斯分布；或者对于另一个特征 x₃ ，可以用它自身的平方根来取代，x₃ 的平方根也就是 x₃ 的 1/2 次方；而这个 1/2 又是另一个可以调整的参数，所以还有 x₄ ，可以用其它数字来替换 x₄ 的指数，比如说 1/3 次幂。所有这些参数（指数参数或是常数参数 c），都是可以调整的参数，目的就是为了让我们的数据看上去更接近高斯分布。

2. 通过误差分析步骤来得到异常检测算法的特征

• 下面我们要介绍的第二个问题是我们如何得到异常检测算法的特征。通常用的办法是，通过一个误差分析步骤，这跟之前讨论监督学习算法时误差分析步骤是类似的，先完整地训练出一个算法，然后在一组交叉验证集上运行算法，然后找出那些预测出错的样本，并看看我们能否找到一些其它的特征来帮助学习算法，让那些在交叉验证集中判断出错的样本表现得更好。

• 让我们通过一个例子来解释一下刚才说的这一过程：
  $$\begin{array}{rl}& \text{Error analysis for anomaly detection }\\ & Wantp(x)largefornormalexamplesx.\\ & p(x)smallforanomalousexamplesx.\\ & Mostcommonproblem:\\ & p(x)iscomparable(say,bothlarge)fornormal\\ & andanomalousexamples\end{array}$$

• 在异常检测中，我们希望 p(x) 的值在正常样本的情况下比较大，在异常样本的情况下比较小。一个很常见的问题是，如果 p(x) 是可比较的，当样本正常和异常时，p(x) 的值都比较大。我们来看一个具体点的例子，假设我们的无标签数据只有一个特征 x₁，要用一个高斯分布来拟合它，假设我们的数据拟合出的高斯分布是这样的（下图上）：
  

• 现在假如我们有一个异常样本，并且假设这个异常样本 x 的取值为 2.5，我们画出异常样本（上图绿色标记），不难发现，它看起来被淹没在一堆正常样本中，它有很高的概率（概率用蓝色曲线的高度表示），而算法没能把它标记为异常样本。如果这代表飞机引擎的制造或者别的什么。那么我们需要做的是看看训练样本，然后看看到底是哪一个具体的飞机引擎出错了，看看通过这个样本能不能启发想出一个新的特征 x₂，来帮助算法找出异常的样本与剩下的红色（正常）的样本的区别，或者说正常的飞机引擎样本。

• 如果我们这样做的话，我们希望的是，能否创建一个新的特征 x₂，使得当我们重新画数据时，如果我们把训练集中的所有正常样本拿出来，应该就会发现，所有的训练样本都是这里（上图下）的红叉了，也希望能看到，对于异常样本，这个特征 x₂ 能发现不寻常的值，因此对于这个绿色的样本，也就是异常样本 x₁ 的值仍然是 2.5，那么 x₂ 很有可能是一个比较大的值，比如 3.5，或者一个非常小的值。

• 现在如果我们再来给数据建模，我们会发现异常检测算法在中间区域的数据有较高的概率，然后越到外层概率越小，到了绿色样本处时，我们的算法会给出很低的概率，所以过程实际就是看看哪里出了错，看看这个算法没有标记出来的异常样本，看看它是否能够启发我们创造一些新特征，所以要找到飞机引擎一些不寻常的地方，并利用它来创造一个新特征，有了这些新的特征，就更容易的将异常样本从正常样本中区别出来，这就是误差分析的过程以及如何为异常检测算法建立新的特征。

3. 选择很大或者很小的特征

• 本节最后，我们来分享一些平时在为异常检测算法选择特征变量时的一些思考。
• 通常来说，我们选择特征的方法是选择那些特别特别大或者特别特别小的特征（那些很可能异常的样本）。我们还是使用监控数据中心的计算机的例子，假设在一个数据中心里，有很成千上万台电脑，我们想知道的是，如果有一台电脑出现故障，做出了奇怪的事情，这里给出了几种可选的特征：
  $$\begin{array}{rl}& \text{Monitoring computers in a data center}\\ & Choosefeaturesthatmighttakeonunusuallylargeor\\ & smallvaluesintheeventofananomaly.\\ & x_1=memoryuseofcomputer\\ & x_2=numberofdiskaccesses/sec\\ & x_3=CPUload\\ & x_4=networktraffic\end{array}$$
• 包括占用内存，磁盘每秒访问次数，CPU 负载，网络流量。假如说我怀疑某个出错的情况在我们的数据集中，CPU 负载和网络流量应该互为线性关系，可能我们运行了一组网络服务器，如果其中一个服务器正在服务很多个用户，那么CPU负载和网络流量都很大。但现在怀疑其中一个出错的情形是我们的计算机在执行一个任务时，进入了一个死循环，如果我们认为其中一个出错的情况是其中一台机器或者说其中一台服务器的代码执行到了一个死循环卡住了，因此CPU负载升高，但网络流量没有升高，因为只是CPU执行了较多的工作，所以负载较大，卡在了死循环里。
  $$\begin{array}{rl}& x_5=\frac{CPUload}{networktraffic}\\ & x_6=\frac{(CPUload{)}^2}{networktraffic}\end{array}$$
• 在这种情况下，要检测出异常，我们可以建立一个新特征 x₅=CPU负载/网络流量。那么这时 x₅ 将会有一个异常大的值，如果某一台机器有较大的CPU负载，但是网络流量正常的话，那么这将会是一个特征，能帮助我们异常检测捕捉到某种类型的异常情况。我们也可以用创建其它的特征来进行检测，比如说有一个特征 x₆，代表CPU负载的平方/网络流量，这就像是特征 x₅ 的一个变体，它仍然是去捕捉某个机器是否有很高的CPU负载，但是却没有同样高的网络流量，通过像这种建立特征的办法，我们就可以捕捉到这些特殊的特征组合所出现的异常值。
• 这节介绍了如何选择特征以及对特征进行一些小小的转换，让数据更接近高斯分布，然后再把数据输入到异常检测算法中。同时也介绍了建立特征时进行的误差分析方法来捕捉各种异常的可能，希望通过这些方法能够帮助我们选择适当的特征，从而帮助我们的异常检测算法捕捉到各种不同的异常情况。

七、多变量高斯分布（Multivariate Gaussian distribution）

• 在这节和下一节中，我们来介绍目前为止我们学习的异常检测算法的一种可能的延伸，这个延伸会用到多元高斯分布（multivariate Gaussian distribution），它有一些优势，也有一些劣势，它能捕捉到一些之前的算法检测不出来的异常。

1. 问题的引入

• 首先我们来看一个例子：
  

• 假设我们有上图这些没有标签的数据，我们要使用数据中心的监控计算机的例子；两个特征变量分别是 x₁ 是 CPU 的负载， x₂ 可能是内存使用量，所以如果我们把这两个特征变量 x₁ 和 x₂ 当做高斯分布来建模，上图右上是特征变量 x₁ 绘制的图，上图右下是特征变量 x₂ 的图，如果我们用高斯分布来拟合，得到如下的两个对应分布：
  $$\begin{array}{r}p(x_1;{\mu }_1,{\sigma }_1^2)\\ p(x_2;{\mu }_2,{\sigma }_2^2)\end{array}$$

• 异常检测算法给 x₁ 和 x₂ 建模以后，现在假设在测试集中，有一个这样的样本，在图中绿色叉的位置，它的 x₁ 的值是 0.4 左右， x₂ 的值是 1.5 左右，现在观察这些数据，看起来它们大部分都在这个范围内（上图左蓝色圈出范围内），所以这个绿色叉离这里看到的任何数据都很远，看起来它应该被当做一个异常数据。在好的样本数据中，看起来 CPU 负载和内存使用量是彼此线性增长的关系，所以如果我们有一台机器 CPU 使用量很高，那么内存使用量也会很高，但是这个绿色样本看起来 CPU 负载很低，但是内存使用量很高，与训练集中的其它样本都不同，看起来它应该是异常的。

• 我们来看一下异常检测算法会怎么做。对于 CPU 负载，这个绿色叉差不多在 0.5 这里，有比较高的可能性它距离其它样本不远，而对于内存使用量，它差不多在 1.5 处，它在这个高斯分布的尾部（上图右下），但是这里的值与看到的其它样本没有太大差别，所以 p(x₁) 会比较高，p(x₂) 也会比较高。但是在上图右上中这个绿叉看起来并没那么差，右下方图中这个绿叉的位置看起来也不那么差。因为有的样本，内存使用量比绿叉对应的样本更高，或者 CPU 使用量更低，所以这个点看起来不是很异常，因此异常检测算法不会将这个点标记为异常。

• 可以发现，异常检测算法不能意识到之上图左中蓝色椭圆所表示的好样本概率高的范围，相反，它认为这部分样本（粉色最小圆范围）是高概率的，外面一些的圈里面的样本是好样本的概率低一些，更外的样本概率更低，它认为那里的绿色叉是好样本的概率挺高，具体来说，它倾向于认为所有在这区域（中等粉圈）中的样本都具有相同的概率，它并不能意识到下边紫色叉位置的其实比上边紫色叉位置的概率要低得多。

2. 多元高斯（正态）分布的具体做法

• 为了解决这个问题，我们要开发一种改良版的异常检测算法，要用到多元高斯分布或者叫多元正态分布，下面是具体做法：
  $$\begin{array}{rl}& \text{Multivariate Gaussian (Normal) distribution}\\ & x\in {\mathbb{R}}^n.Don’tmodelp(x_1),p(x_2),...,etc.separately.\\ & Modelp(x)allinonego.\\ & Parameters:\mu \in {\mathbb{R}}^n,\Sigma \in {\mathbb{R}}^{n\times n}(covariancematrix)\end{array}$$

• 我们有特征变量 x，它属于 Rⁿ，不要为 p(x₁)和p(x₂)分别建模，而是要建立一个整体的 p(x) 模型，就是为所有 p(x) 建立统一的模型。多元高斯分布的参数是向量 μ 和一个 n×n 的矩阵 Σ，Σ 被称为协方差矩阵，它类似于我们之前在学习 PCA（主成分分析算法）的时候所见到的协方差矩阵。为了完整起见，下面写出多元高斯分布的公式，确定 x 的概率的参数是 μ 和 Σ：
  $$\begin{array}{r}p(x;\mu ,\Sigma )=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}exp\left(-\frac{1}{2}(x-\mu {)}^{\top }{\Sigma }^{-1}(x-\mu )\right)\end{array}$$

• |Σ| 是 Σ 的行列式，我们可以在 Octave 中使用 det(Σ) 来计算它，在上面的式子中，Σ 是一个 n×n 的矩阵，而不是求和符号。
  $$\begin{array}{rl}& \Sigma :Sigma\\ & \sum :sum\end{array}$$

• 上面这些就是这就是 p(x) 的公式，但是对我们来说，更有趣、更重要的是，p(x) 到底是什么样子，我们来看一下多元高斯分布的例子。

3. 多元高斯分布的例子

• 我们来看一个二维的例子：
  

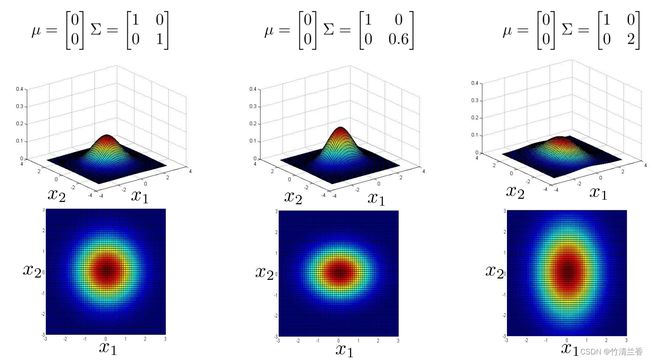
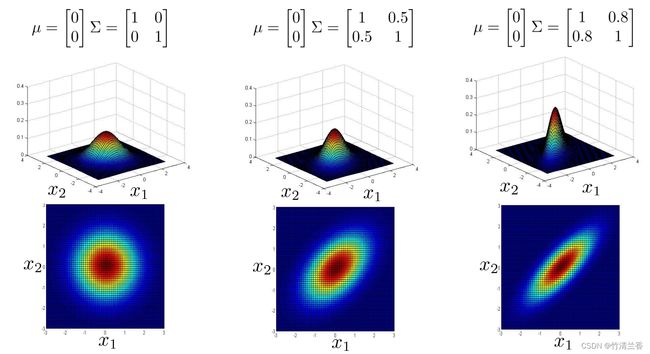
• 如果 n 等于 2，有两个特征变量 x₁ 和 x₂，我们让 μ 等于 0，让 Σ 等于上图左对应的单位矩阵（对角线上的值为 1，费对角线上的值为 0），在这个情况下，p(x) 看起来是如上图左所示那样的。对于一个特定的 x₁ 和一个特定的 x₂，三维图形中对应的高度就是 p(x) 的值，所以在这个参数设定下，p(x) 在 x₁ 和 x₂ 都等于 0 时，取到最高值，那就是高斯分布的峰值，然后这个概率，这个二元高斯分布随着这个二维钟形的面衰减，下面的平面图和三维图是一样的，但它是用等高线，或者说不同颜色画的图，所以中间很深的暗红色对应的是最高值，然后这个值降低，黄色表示低一点儿的值，青色表示更低一些的值，深蓝色表示的是最低的值，所以这个其实是同一张图，不过使用了俯视的角度，并且用颜色来区别。所以从这个分布我们可以看出，大部分概率都在 (0,0) 附近，然后，随着 (0,0) 这个点往外延伸， x₁ 和 x₂ 的概率下降。

• 现在来试试改变一些参数，会发生什么，假设我们缩小一下 Σ，Σ 是一个协方差矩阵，所以它衡量的是方差，或者说特征变量 x₁ 和 x₂ 的变化量，所以如果缩小 Σ，那么结果就是，这个鼓包的宽度会减小，高度会增加一些，因为在这个面以下的区域等于 1，所以这个面以下的体积积分等于 1，因为概率分布的积分必须等于 1。如果我们缩小方差，相当于缩小 Σ 的平方，会得到一个窄一些，高一些的分布。从平面图（上图中）中我们也看到，这些同心椭圆也缩小了一些。

• 相反，如果把 Σ 对角线上的值增加到 2，那么最后会得到一个更宽更扁的高斯分布（上图右），虽然很难看出来，但是它还是一个钟形的鼓包，它只是扁平了很多，他变得更宽了，所以 x₁ 和 x₂ 的方差或者变化量变大了。
  

• 下面再举几个例子（上图），现在我们试一下一次改变 Σ 的一个元素，假如我们把 Σ 改为 0.6 和 1（上图中），它所做事情是减小第一个特征变量 x₁ 的方差，同时保持第二个特征变量 x₂ 的方差不变，在这个参数设置下，就可以给这样的东西建模， x₁ 有小一些的方差，而 x₂ 有大一些的方差，而如果再换一种做法，把 Σ 矩阵设为 2 和 1（上图右），那么我们也可以建立这样的模型， x₁ 的变化范围比较大，而 x₂ 的变化范围则窄一些，它也被反映到上面的图上了，这个分布随着 x₁ 远离 0，下降得更缓慢，而随着 x₂ 远离 0，下降得非常快。

• 类似地，如果我们改变 Σ 矩阵对角线上别的元素，类似于上一张图片，我们可以得到线面这张图：
  

• 我们可以发现现在 x₂ 的变化区间比原来的例子要小很多（上图中），通过将 Σ 矩阵对角线上相应的元素改成 2，我们就可以得到 比较大的 x₂ 的变化区间（上图右）。
  

• 多元高斯分布的一个很棒的事情是，你可以用它给数据的相关性建立模型，我们可以用它来给 x₁ 和 x₂ 高度相关的情况建立模型，所以具体来说，如果我们改变协方差矩阵非对角线上的元素，我们会得到一种不同的高斯分布（上图中），所以当我们将非对角线的元素从 0.5 增加到 0.8 时，我们会得到一个更加窄和高的，沿着 x = y 这条线的分布，然后这个等高图告诉我们 x 和 y 看起来是一起增加的，概率高的地方是这样的，要么 x₁ 很大 x₂ 也很大，或者 x₁ 很小 x₂ 也很小，或者是这两者之间，然后随着这个值 0.8 变大，得到的高斯分布概率分布落在这个狭窄的区域（x 接近于 y），这在 x 接近 y 的区间内是一个很高很细的分布，几乎都在中间（上图右）。
  

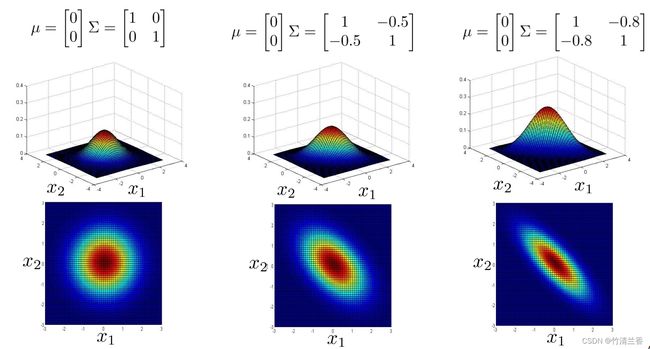
• 这是当我们把这些元素设置为正值时。相反，如果我们把它们设置为负值，然后把这个值减少到 -0.5 或者减少到 -0.8，然后得到的模型是大部分的概率都在 x₁ 和 x₂ 负相关这样一个区域（上图中）。所以大多数概率都落在 x₁=-x₂ 附近的区域（而不是 x₁=x₂），因此这个捕捉到了 x₁ 和 x₂ 的负相关。
  

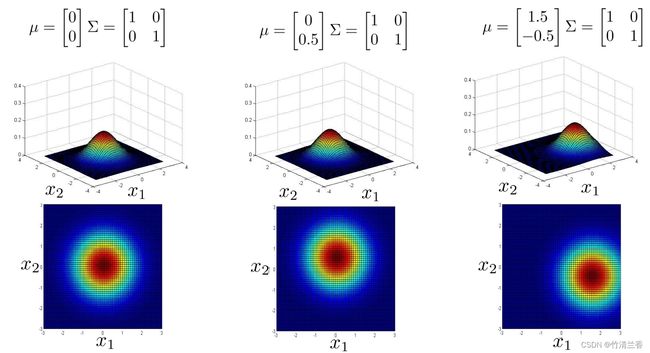
• 上面的讲解主要说明了多元高斯分布能捕捉到的不同的分布，到目前为止我们一直在改变协方差矩阵，另外我们还可以改变平均参数 μ，一开始我们有 μ 中的元素全为 0，所以分布集中在 x₁ = 0，x₂ = 0 这个点周围，所以这个分布的峰值在图像的中心处（上图左）；如果改变μ的值，它就会改变这个分布的峰值，如果 μ 等于 0、 0.5，这个峰值就在 x₁ = 0，x₂ = 0.5，峰值的位置就发生了改变（上图中），如果再次改变 μ ，那么峰值就会移动到另一个位置（上图右），所以改变参数 μ 的值，就是在移动整个分布的中心。

• 多元高斯分布所能描述的概率分布最重要的优势就是能够让我们描述两个特征变量之间可能存在正相关或者是负相关的情况。

• 下一节我们将把多元高斯分布函数应用到异常检测中。

八、使用多变量高斯分布检测异常（Anomaly detection using the multivariate Gaussian distribution）

• 上一节我们谈到了多元高斯分布，并且看到了一些通过改变参数 μ 和 Σ，对这些分布进行建模的例子。本节我们将采用这些思想，并应用于开发一个不同的异常检测算法。

1. 多元高斯分布

①公式及参数回顾

• 首先回顾一下多元高斯（正态）分布：
  $$\begin{array}{rl}& \text{Parameters}\mu ,\Sigma \\ & p(x;\mu ,\Sigma )=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}exp\left(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\right)\end{array}$$
  

• 有两个参数 μ 和 Σ，其中 μ 是 n 维变量，而 Σ 是个 n×n 的协方差矩阵，而这里的公式 p(x) 参数为 μ 和 Σ ，我们可以通过改变 μ 和 Σ 来得到范围内一个不同的分布，这里的三个样本在上一节学习过学习过。

②参数估计

• 下面我们来谈谈参数的拟合或者说参数估计问题：
  $$\begin{array}{rl}& \text{Parameter fitting:}\\ & \text{Given training set}\{x^{(1)},x^{(2)},...,x^{(m)}\}x\in {\mathbb{R}}^n\\ & \mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)}\Sigma =\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu )(x^{(i)}-\mu {)}^T\end{array}$$
• 还是那个问题，假如我有一组样本，从 x¹ 到 x^m，这些样本的每一个都是n维向量，并且我的样本是服从多元高斯分布的，那么我应该如何去估计参数 μ 和 Σ 呢？对于估计参数，有一个标准公式，就是只要设 μ 为你的训练样本平均值，同时设 Σ 也等于此，这和我们之前使用 PCA（主成分分析算法）的时候，写的 Σ 是一样的，所以你只要把它代入到公式里，就能估计参数 μ 和参数 Σ 了。
• 在给定数据集以后，这就是如何去估计 μ 和 Σ，让我们采用这个方法，并将其代入到异常检测算法中，那么如何把这些东西都综合起来，来开发一个异常检测算法呢？以下就是具体方法：

2. 异常检测算法开发（采用多元高斯分布）

$$\begin{array}{rl}& \text{Anomaly detection with the multivariate Gaussian }\\ & 1.Fitmodelp(x)bysetting\\ & \mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)}\\ & \Sigma =\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu )(x^{(i)}-\mu {)}^T\end{array}$$

• 首先用我们的数据集来拟合该模型，通过设定 μ 和 Σ 来拟合 p(x)。

• 接下来当我们有一个新样本 x，即一个测试样本，假设这里是我们的新样本（下图绿色叉），同时也是测试样本：
  

• 得到这个样本 x 后，我们需要用这个多元高斯分布的公式来计算 p(x)，如果得到 p(x) 很小（即 p(x) < ε），就标记该样本为异常，如果 p(x) 大于参数 ε，就不进行异常标记。
  $$\begin{array}{rl}& 2.Givenanewexamplex,compute\\ & p(x)=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}exp\left(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\right)\\ & Flagananomalyifp(x)<\epsilon \end{array}$$

• 如果我们将多元高斯分布拟合到数据集中，也就是这些红色的叉中，而不包括绿色的叉，会得到一个高斯分布，该分布在数据中央的区域，有很大的概率值，每往外一些概率就减少一些，到了最外层一圈，它对应的概率已经很低了，如果我们将多元高斯分布应用到这个样本上，它就能正确标记出这个样本（绿色叉）确实是一个异常。

3. 多元高斯分布模型和原始模型的关系

• 最后，有必要再说几句，多元高斯分布模型和原始模型有着怎样的关系呢？
  $$\begin{array}{rl}& \text{Original model :}\\ & p(x)=p(x_1;{\mu }_1,{\sigma }_1^2)\times p(x_2;{\mu }_2,{\sigma }_2^2)\times \cdot \cdot \cdot \times p(x_n;{\mu }_n,{\sigma }_n^2)\end{array}$$

• 原始模型就是 p(x₁) p(x₂) 到 p(x_n) 的乘积。事实上我们可以用数学方法来推倒多元高斯模型和这个原始模型之间的区别，特别是，原始模型对比多元高斯模型，多元高斯模型的等高线总是轴对齐的，事实上下面 3 个服从高斯分布的样本我们都可以用原始模型来拟合。
  

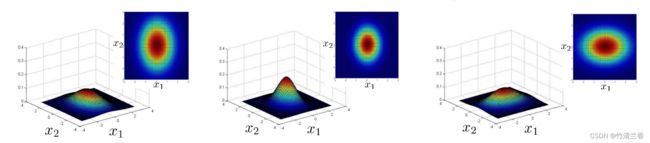
• 实际上，对于多元高斯分布，这些椭圆的分布轮廓（等高线），这种模型实际上对应一种特殊情况下的多元高斯分布。这种特殊情况是通过限制 p(x) 的分布，即 p(x) 的多元高斯分布来定义的，所以这个轮廓由这个概率分布方程得到的椭圆是轴对齐的，所以能得到 p(x)。注意到，在这3个例子中，这些椭圆形它们的轴都是与 x₁ 和 x₂ 轴对齐的，而不是前面那种矩阵非对角线有非零元素、图像的轴有倾斜的情况。
  实际上，可以用数学来证明，上面这个模型（原始模型）实际上就是某种特殊情况下的多元高斯分布:
  $$\begin{array}{rl}& \text{Corresponds to multivariate Gaussian :}\\ & p(x;\mu ,\Sigma )=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}exp\left(-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\right)\\ & where\\ & \Sigma =\left[\begin{array}{cccc}{\sigma }_1^2& 0& 0& 0\\ 0& {\sigma }_2^2& 0& 0\\ 0& 0& ...& 0\\ 0& 0& 0& {\sigma }_n^2\end{array}\right]\end{array}$$

• 这个情形就是当它的协方差矩阵 Σ 在非对角线上都是 0 的时候（如上面矩阵所示），如果把原始模型中的 σ² 放进上面的协方差矩阵中，这时这两个模型就会完全相同，也就是说如果这个用了多元高斯分布的新模型比起之前旧的模型，如果它的协方差矩阵 Σ 在非主对角线都是 0，那么这个新的对应高斯分布的模型，它的分布方程的轮廓（平面图中的等高线）就是轴对齐的，所以我们不能对不同特征之间的关系进行建模，这个意义上的原始模型只是高斯模型的一种特殊情况。

4. 多元高斯分布模型和原始模型的选择

Original model	Multivariate Gaussian
①Manually create features to capture anomalies where x1,x2 take unusual combinations of values.	②Automatically captures correlations between features
③Computationally cheaper ( alternatively, scales beger to large n ).	④Computationally more expensive
⑤OK even if m (training set size) is small	⑥Must have m>n, or else Σ is non-invertible.

• 那么如何在两个模型间进行选择呢？什么时候应该用原始模型，什么时候又该用多元高斯模型呢？其实原始模型被使用得更频繁一些，反之多元高斯模型用的要少一些，但是它在捕捉特征间的关系方面有着很多优点。

• 假设我们进行异常检测，有一些不同的特征 x₁，x₂ 等，我们想通过异常的组合值来捕捉异常样本。比如，在之前的例子中，我们有这样的样本，它出现异常通常是在 CPU 负载以及内存使用有着异常的组合值的时候。①如果我们用原始模型来捕捉这一点，我们就需要创建一个额外的特征，比如令新特征 x₃ = x₁/x₂，它可能等于 CPU 负载除以内存使用，或者别的东西，我们需要创建这样的新特征来捕捉异常的组合值，因为 x₁ 和 x₂ 组合值出现异常的时候，可能 x₁ 本身和 x₂ 本身看起来都是很正常的值。如果我们花费时间来手动创建这样一个新特征，原始模型就能运行得很好，②相比之下，多元高斯模型就能自动地捕捉这种不同特征之间的关系。

• ③不过原始模型也有它自己优点，原始模型的一个巨大优势就是它的计算成本比较低，换一种说法就是它能适应巨大规模的 n，即适应数量巨大的特征，当 n = 10000，甚至 n = 100000 的时候，原始模型都能运行得很好。④而对于多元高斯模型，需要计算 Σ 矩阵的逆矩阵，而 Σ 是一个 n×n 矩阵，如果它计算的 Σ 是个 100000×100000 的矩阵，那么计算成本将会非常高昂，所以多元高斯模型能适应的 n 值的范围比较小。

• ⑤最后，对于原始模型，即使我们有一个较小的有一定相关性的训练集也能顺利运行，这是一个较小的无标签样本，用来拟合模型 p(x)，即使 n 的值只有 50、100 这样，它也能工作得很好，⑥而对于多元高斯分布，这个算法有一些数学性质，也就是必须保证 m>n，也就是样本的数量要大于特征的数量。如果在估计参数时，我们不能满足这个数学性质（即如果 m ≤ n），那么这个矩阵 Σ 就会是不可逆的（或者说是个奇异矩阵），我们无法使用多元高斯模型，除非我们对它进行修改。

• 在这个方面我们有一个原则，就是我们会使用多元高斯模型，当且仅当 m 远大于 n 时，这算是一种狭义的数学要求。在实践中，我们会用多元高斯模型，仅当 m 远大于 n 的时候，所以如果m ≥ 10n，那么这时候我们就可以用多元高斯分布了，如果不能满足这一点，那么多元高斯模型就会有很多参数，因为这个协方差矩阵 Σ 是个 n×n 的矩阵，所以它大概会有 n 的平方个参数，因为它是个对称矩阵，实际上参数的数量更接近于 n 的平方除以 2，但这还是很多，所以要确保我们有一个相当大的 m 值，确保我们有足够的数据来拟合这些变量，所以 m ≥ 10n 算是一个合理的使用原则来确保它能够很好地去估计协方差矩阵 Σ 。

• 因此在实践中，原始模型会用的多一些，如果我们觉得需要捕捉具有相关性的特征，这时人们常常做的是手动设计一些像上面提到的 x₃ 这样的新特征来捕捉那些异常的组合值，但是当我们有一个很大的训练集或说 m 很大而 n 不是很大的时候，这时多元高斯模型会更值得考虑，有更好的效果，可以节省我们在手动创建这些额外变量所花费的时间去捕捉这些能用异常的组合值来体现的异常样本。

• 最后想简明地再提一下，一个技术上的问题，如果我们在拟合多元高斯模型的时候，发现协方差矩阵 Σ 是奇异的（不可逆），那么通常是两种情况，一种是我们没有满足 m > n 的条件，第二种是我们存在冗余的特征（也就是存在两个变量线性相关），虽然不可逆的情况很少发生，但是万一我们实现一个多元高斯模型时，我们发现 Σ 不可逆，这时首先确保 m 远大于 n，其次检查一下有没有冗余特征，如果有两个重复特征，那么就去掉一个。

总结

• 本篇文章主要介绍了异常检测，首先对问题进行了直观的描述，随后定义了异常检测，如果一个样本出现的位置对应的概率低于我们要求的阈值，那么它就会被定义为一个异常点，同时对于异常检测问题，我们也举出了实际中的几个应用例子。
• 高斯分布部分介绍了高斯函数的图像特征， μ 和 σ 的变化对图像会产生什么样的影响同时如何去求这两个参数，以及如何通过高斯函数来拟合数据。
• 算法部分我们讨论了如何估计 p(x) 的值，即 x 的概率值，使得我们可以开发出一种异常监测的算法，同时也介绍了如何对给定数据集拟合参数，对参数进行估计来得到 μ 和 σ 的值，并且对于新的例子我们也说明了其是否为异常。
• 在开发和评估异常检测系统中，我们讨论了评估一个异常检测算法的步骤，并且再次强调，在进行决策时（如参数 ε 的选择、特征的选择等等），用一个像 F₁-score 这样的实数进行算法的评估，能够大大提高我们开发一个异常监测系统的效率。除此之外，我们还提到了一个比较推荐的划分带标签和无标签的数据的方法，即采用 6：2：2 的比例来分配正常样本，而对于异常样本，我们只把它们放在交叉验证集和测试集中；同时也提出了不推荐的做法，即把同样的数据同时用于交叉验证集和测试集（无论正常或异常样本都不好）
• 在特征的选择中，如果画出的数据直方图看起来与高斯分布相差甚远，那么我们就有必要进行一些不同种类的转换（改变指数参数或是对数里加上的常数），通过这些方法，让我们的数据更接近高斯分布，然后再把数据放到学习算法中（虽然不这么做也可以，但我们通常还是会进行这一步）。同时也介绍了建立特征时进行的误差分析方法来捕捉各种异常的可能，希望通过这些方法能够帮助我们选择适当的特征，从而帮助我们的异常检测算法捕捉到各种不同的异常情况。
• 多元高斯分布所能描述的概率分布最重要的优势就是能够让我们描述两个特征变量之间可能存在正相关或者是负相关的情况。
• 在使用多元高斯分布来做异常检测中，如果应用该方法，我们将能拥有一个异常检测算法来自动地捕捉正样本和负样本各种特征间的联系。如果它发现某些特征的组合值是异常的，就会将其标记为异常样本。