SIR模型和Python实现

一、SIR模型介绍

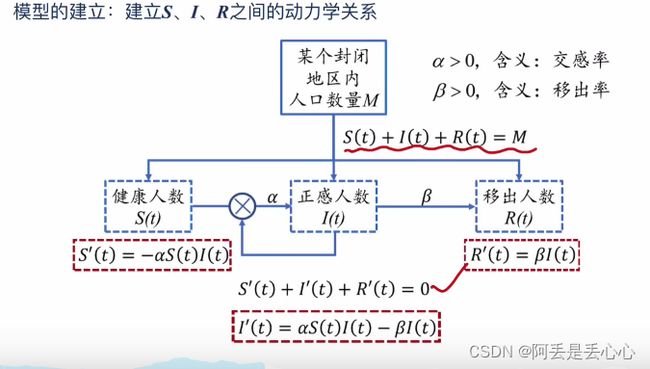
SIR模型时传染病中最基础最核心的模型，研究的是某个封闭地区的疫情传播规律。

SIR模型的动力学关系如下图：

健康人数S的变化与 健康人数S和正感人数I的乘积（代表健康人数和正感人数的接触）成正比，其中α代表交叉感染率

移出人数的变化与正感人数的数量成正比，其中β代表回复率。

基于上面的是自，SIR模型可以表示成一个常微分方程组如下图：

 当s(t)=β/α时就是病毒最严重的时候；

表示S的反函数，代表S越大，t越小，越早结束疫情

封城就是为了较低交叉感染率α，并提高治愈率β

以上就是关于SIR模型的简单介绍，我是从B站上学习到的，更多可以看遇见数学的视频：数学建模系列之SIR传染病模型（1）——模型的建立与演绎_哔哩哔哩_bilibili

接下来我将用Python实现SIR模型在某真实社交网络（基于networkx）上的传播过程模拟。

代码参考了这篇文章：人群接触网络中的 SIR 疫情模拟 - 云+社区 - 腾讯云

二、接触网络中的SIR模型

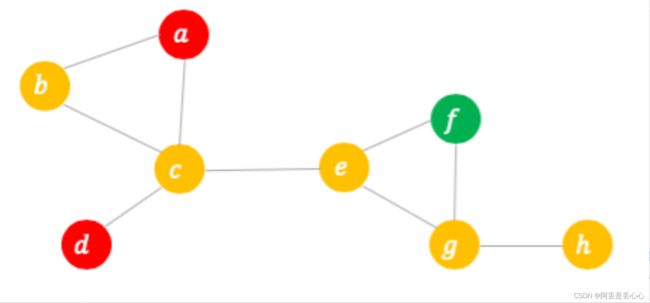
在 SIR 模型中，假设人之间是随机接触的。如果人之间的接触关系不是随机的，而是形成了一个接触网络。那么在这个网络中，每个人接触到感染者的概率不再相等，而与他在网络中的位置相关。

 比如对于这张图，c接触到感染者的概率远远大于h，因此其染病的概率也会更高。

因此我们可以更新SIR模型的规则：（这也是参考了上面腾讯云的文章）

与传统 SIR 模型类似，有两个重要的参数：感染率 α 和恢复率 β。我们需要给每个节点引入一个状态，取值为 S,I,R 中的一种。每一个时间步中，需要动态对每一个节点的状态进行更新。更新规则如下：

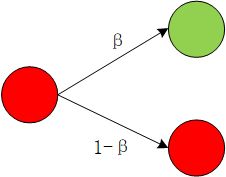
• 如果当前节点是恢复者，则下一步，节点状态依然是恢复者。​

• 如果当前节点是感染者，则下一步，β的概率转化为恢复者。1 - β的概率依然是感染者。

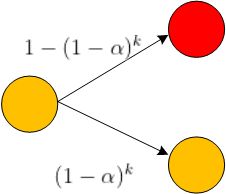
• 如果当前节点是易感者（健康者），则需要计算其邻居节点中感染者的数量，假设其有 k 个邻居为感染者。则该节点下一步转化为感染者的概率为 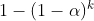，否则继续保持易感者状态。

         下面这个概率的含义就是对于每个邻居感染者，易感者有1-α的概率保持健康，故有概率保持健康

三、Python实现SIR模型

1.导入数据

这里我导入的是一个节点表和一个边表，边表用来构建网络图，节点表用来选择初始感染者：

import pandas
import csv
import random

node_df = pandas.read_csv('E:/data/节点.csv')
all_nodes_list = node_df.values.tolist()  #获取文件中所有节点

edge = []   #获取所有边
with open('E:/data/边.csv','r',encoding='utf-8-sig') as f: 
    data = f.readlines()  
    for line in data: 
        line = list(line.replace('\r','').replace('\n','').replace('\t','').split(','))
        single_edge = tuple([line[1],line[4]])
        edge.append(single_edge)

2.绘制初始网络

所有节点都是健康的

import networkx as nx
ba = nx.Graph()
ba.add_edges_from(edge)
for node in ba.nodes():
    ba.nodes[node]["state"] = "S"

3. 更新网络节点状态

先考虑单个节点的更新

我们使用一个简单的函数来实现一个节点的状态的更新。

首先，如果一个节点是恢复者，那么下一步还是恢复者，其节点状态保持不变。 如果一个节点是感染者，那么其恢复的概率是 β。用程序实现的方法为，先均匀生成一个0到1的随机数 p，如果 p < β，则节点恢复，否则节点依然处于感染状态。

如一个节点是易感者，先要去其邻居节点中看看一共有多少个邻居是感染者，有 k 个邻居是感染者，那么当前节点被感染的概率是 1 - (1 - α)k。我们生成一个0到1的随机数 p，如果 p < 1 - (1 - α)k，则节点被感染，否则不被感染。

import random

# 根据 SIR 模型，更新单一节点的状态
def updateNodeState(G,node, alpha, beta):
    if G.nodes[node]["state"] == "I": #感染者
        p = random.random() # 生成一个0到1的随机数
        if p < beta:   # gamma的概率恢复
            G.nodes[node]["state"] = "R" #将节点状态设置成“R”
    elif G.nodes[node]["state"] == "S": #易感者
        p = random.random() # 生成一个0到1的随机数
        k = 0  # 计算邻居中的感染者数量
        for neibor in G.adj[node]: # 查看所有邻居状态，遍历邻居用 G.adj[node]
            if G.nodes[neibor]["state"] == "I": #如果这个邻居是感染者，则k加1
                k = k + 1
        if p < 1 - (1 - alpha)**k:  # 易感者被感染
            G.nodes[node]["state"] = "I" 

再对网络中所有节点进行更新

def updateNetworkState(G, alpha, beta):
    for node in G: #遍历图中节点，每一个节点状态进行更新
        updateNodeState(G,node, alpha, beta)

用函数countSIR统计三类人群数量

# 计算三类人群的数量
def countSIR(G):
    S = 0;I = 0
    for node in G:
        if G.nodes[node]["state"] == "S":
            S = S + 1
        elif G.nodes[node]["state"] == "I":
            I = I + 1
    return S,I, len(G.nodes) - S - I    

所有函数都准备好后，我们进行网络和参数初始化设置

#随机选取一个节点为初始感染者  
ba.nodes["123549878"]["state"] = "I" 

days = 50 #设置模拟的天数
alpha = 0.0003 #感染率
beta = 0.10 #恢复率

#设置不同人群的显示颜色，易感者为橘色，感染者为红色，恢复者为绿色
color_dict = {"S":"orange","I":"red","R":"green"} 

在图中开始SIR模型的模拟，设置模拟天数，开始执行模拟过程

# 模拟天数为days，更新节点状态
import matplotlib.pyplot as plt
#fig,ax = plt.subplots(111)
%matplotlib inline
import time
SIR_list = []
for t in range(0,days):
    updateNetworkState(ba,alpha,beta) #对网络状态进行模拟更新
    SIR_list.append(list(countSIR(ba))) #计算更新后三种节点的数量

模型结果可视化

df = pd.DataFrame(SIR_list,columns=["S","I","R"])
df.plot(figsize=(9,6),color=[color_dict.get(x) for x in df.columns])

我的数据得到的结果如下

 我的网络结果中分为几个隔离比较大的社区，所以有一部分人群始终没有被感染。

4.探究不同节点作为初始感染者传播网络的区别

比如我想知道在一个网络中的谣言传播情况，想看看随机选一个节点，通过这个节点看看最后有多少个人会接触到这个谣言（其实就是传播停止时的恢复者）

import matplotlib.pyplot as plt
import time
import pandas as pd
#fig,ax = plt.subplots(111)
%matplotlib inline
import time
# 获得所有节点的属性
def get_last_node_state(all_nodes_list,G):
    SIR_result = []
    for item in all_nodes_list:
        node_attri = []
        node_attri.extend(item)
        try:
            for node in G.nodes():
                G.nodes[node]["state"] = "S"   #将网络中所有节点设为健康者
            G.nodes[str(item[0])]["state"] = "I"    #将某一节点设为感染者
            for t in range(0,days):
                updateNetworkState(G,beta,gamma)  #对网络状态进行模拟更新
            node_result = pd.DataFrame([i[1] for i in G.nodes(data=True)], index=[i[0] for i in G.nodes(data=True)])
            state_count = node_result.groupby('state')['label'].count().to_dict() #按感染情况分组
            R_count = state_count['R']   #计算恢复者数量
            node_attri.append(R_count)
            SIR_result.append(node_attri)
        except Exception as e:
            print(e)              
    return SIR_result   #返回结果形式为[节点id,节点接触到的人数（恢复者人数）]

#执行函数
SIR_result = get_last_node_state(all_nodes_list,ba)