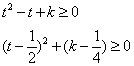【经典面试题】实现平方根函数sqrt

/*************************************************************************
 * 作者：xusiwei1236([email protected])
 * 出处：http://blog.csdn.net/xusiwei1236
 * 声明：转载请注明出处，请勿用于商用.
 *       对本文所涉及的主题如有任何观点、想法，欢迎交流（email或评论）
 ************************************************************************/

本文将从一道经典的面试题说起：实现平方根函数，不得调用其他库函数。

函数原型声明如下：

double Sqrt(double A);

二分法

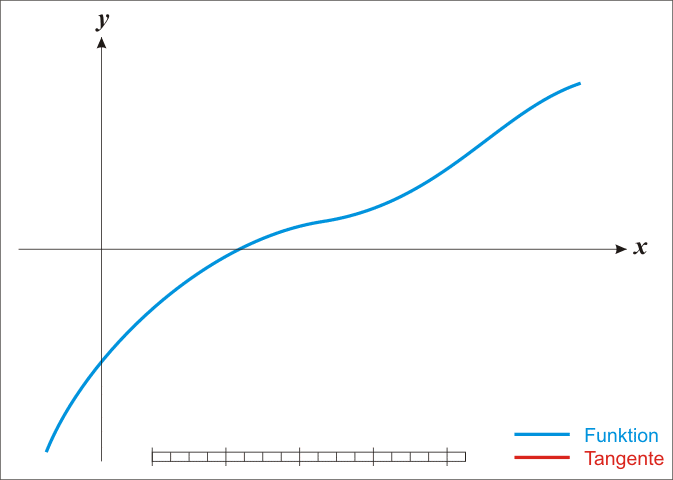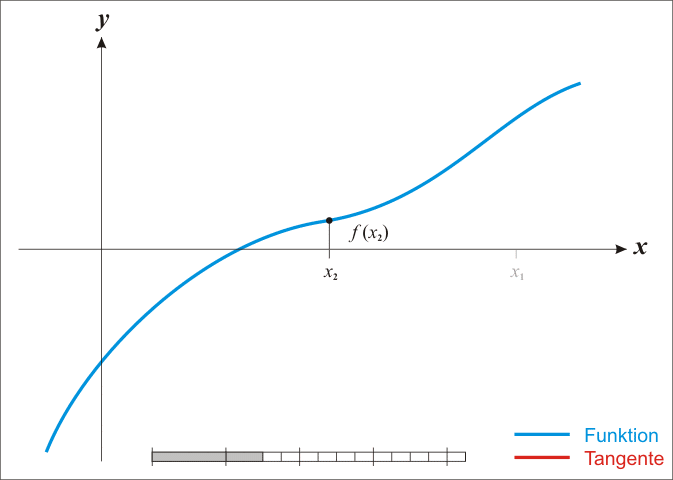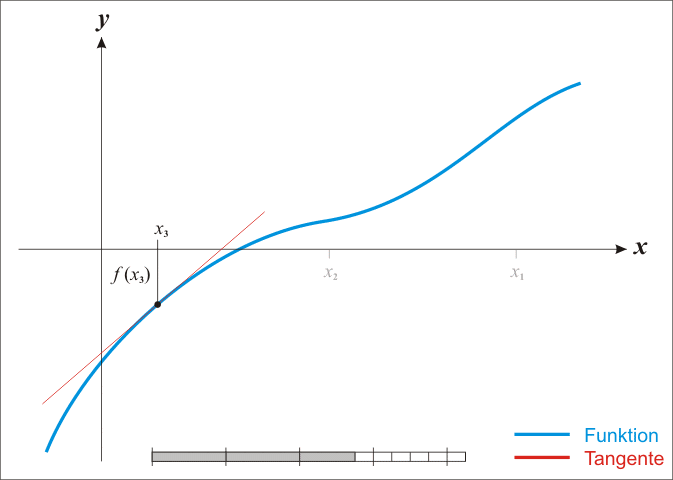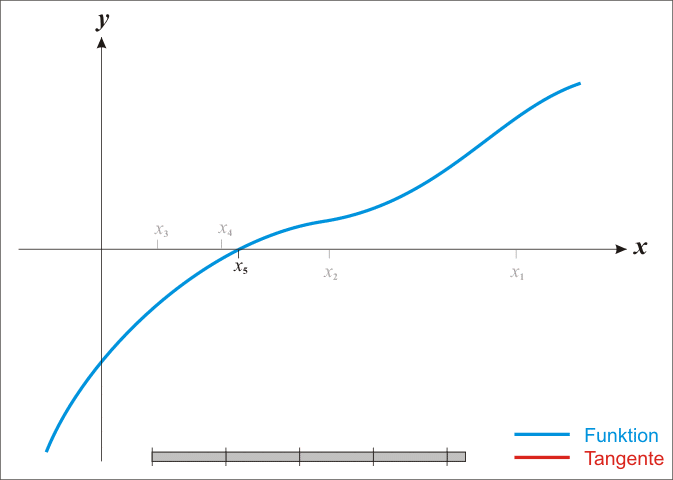
二分法的概念

求，等价于求方程的非负根（解）。求解方程近似根的方法中，最直观、最简单的方法是二分法。“二分法”算法步骤如下：

1. 先找出一个区间 [a, b]，使得f(a)与f(b)异号。
2. 求该区间的中点 m = (a+b)/2，并求出 f(m) 的值。
3. 若 f(m) * f(a) < 0 则取 [a, m] 为新的区间, 否则取 [m, b].
4. 重复第2和第3步至理想精确度为止。

二分法的过程可用下图表示：

初始区间的选定

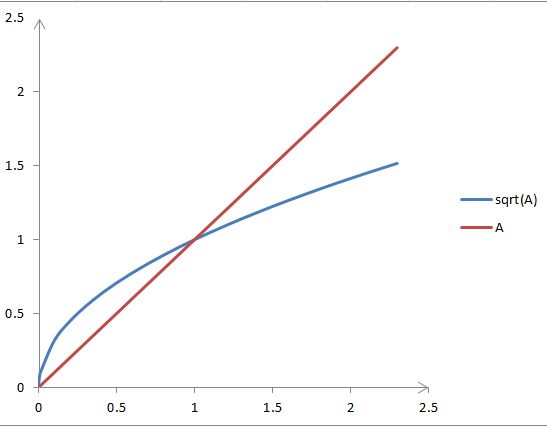
可见，若要用“二分法”求方程，首先要找到一个区间 [a, b]，使得f(a)，f(b)异号。a可以取0，这很容易想到；但b如何选取，即如何选取b=f(A)，使得？

取f(A)=A？不行，因为它不能始终保证：

从图像可知，当A>1时，才有。若用A作为第一步的上界，则在A小于1时，将无法得到正确结果。

同时可知，sqrt(A)在原点处的切线平行于y轴，所以找不到常数项为零的多项式f(A)，使得。

据此，可推出一个，使得成立。

令，则t>=0，， 等价于，即

显然，当时，上式成立，所以k可以取[1/4, +∞)的任意值，不妨取k=1/4，即有

，使得成立。

二分法的误差

为了说明二分法的误差，需要借助一个定理。
零点定理：若f(x)在(a,b)连续，且f(a)f(b)<0，则f(0)在(a, b)内有零点。
二分法每次迭代都能够保证实际解在区间[a, b]范围内，所以每次迭代的误差都小于当前区间的宽度，这也是迭代的结束条件（通常误差给定）。

二分法实现sqrt

根据以上分析，可以很快写出sqrt的“二分法”版本：

double Sqrt(double A)
{
	double a = 0.0, b = A + 0.25, m; // b = A 是错误的上界
	
	// while(b - a > 2*DBL_EPSILON) { // sometimes dead cycle when m==a or m==b.
	for(;;) {
		m = (b + a)/2;
		if( m-a < DBL_EPSILON || b-m < DBL_EPSILON ) break; 
		if( (m*m - A) * (a*a - A) < 0 ) b = m;
		else a = m;
	}
	return m;
}

需要注意的是：

• 初始上界是A+0.25，而不是A；
• double型的精度DBL_EPSILON，不能随意指定；

牛顿迭代法

下面介绍另一种应用广泛的方法——牛顿迭代法。

牛顿法的概念

牛顿迭代法是迭代法的一种，它的迭代格式为：

 

牛顿法具有明显的几何意义，x[k+1]正是曲线在x[k]处的切线与x轴的交点的横坐标。因此，牛顿法也称切线法。

来自Wikipedia的一个动态图很好的解释了这种几何意义：

牛顿法初值的选定

在开始牛顿迭代法之前，需要选定一个d迭代初值x0。根据前文分析，求sqrt(A)，也可以取x0 = A+0.25；

牛顿法sqrt

根据牛顿法，求即求的非负根，，
所以，此时的牛顿递推式为：
 

离实现牛顿法还差关键一步：迭代的结束条件。

在不知道误差公式，且要求误差尽可能小情况下可以使用另一种方法——限定f(x)=0的误差（此法仅限于不给误差范围，且要求误差尽可能小时使用）。

据此，实现的sqrt如下：

double Sqrt(double A)
{
	double x0 = A + 0.25, x1, xx = x0;
	for(;;) {
		x1 = (x0*x0 + A) / (2*x0);
		if(fabs(x1 - x0) <= DBL_EPSILON) break;
		if(xx == x1) break; // to break two value cycle.
		xx = x0;
		x0 = x1;
	}

	return x1;
}

这段程序里的while条件是fabs(x1*x1-A) > 5*DBL_EPSILON是因为，x的误差在2*DBL_EPSILON范围内，所以x*x的误差就在4*DBL_EPSILON范围，考虑到浮点乘法的精度丢失，所以为5*DBL_EPSILON。

迭代法的理论基础

迭代格式收敛的前提

迭代法在进行“迭代”之前，需将原方程改写成的形式；再用迭代格式，逐次逼近的实际解x*。

整个过程的所有x构成了数列：（迭代序列），数列的递推式即；

所以，迭代法能够求得近似解的前提是

         

其中x*为方程的实际解。

迭代格式收敛的条件

迭代法收敛的前提是 ，这很好理解；但要用此式验证迭代式是否收敛，必须先通过递推式求出通项；

是否有更简单的方法判定迭代格式收敛？当然有，下面介绍一个定理能够简便的判定迭代格式是否收敛，同时也能判定误差。

---

定理  迭代格式收敛条件（Vipschitz条件）

若迭代函数满足：

①一阶导数连续；

②当x∈[a, b]时，有；

③存在常数，使得；

则

1. 方程有唯一根x*；
2. 对任意x0∈[a, b]，迭代格式收敛，且；
3. ，（事后误差估计）；
4. ，（事前误差估计）；
5. 

---

定理应用

下面以求的近似解为例，说明定理如何用：

1）判断收敛

对应的迭代函数为：

它的导函数为：

在[0, A+0.25]区间内它显然连续，且存在L=1/2使得；；即满足收敛的三个条件；

2）估计误差（迭代次数）

有了L = 1/2；就可以根据定理估算：

①给定误差情况下，需要迭代几次？

②给定迭代次数，最终近似解的误差？

比如，假设题目要求的精度是：小数点后2位（精确到0.01），那么误差要小于0.01 / 2 = 0.005；只需根据初值x0和第一次迭代结果x1和定理的结论4，便可算出迭代次数k，这里不再罗列（公式编辑起来比较麻烦）。

同样，根据x0，x1和结论4，也可以很方便的算出第k次迭代的误差；

推广——一般方程求近似解

本文指出的二分法、牛顿迭代法是求解方程近似解的常见方法，不仅仅限于求sqrt，但在本文所实现的sqrt程序的基础上，可以很快实现求解其他方程的程序。

二分法

比如，如下程序段就是二分法求解任意方程f(x)=0的程序：

double bisection(double (*f)(double), double a, double b, double eps)
{
	double m;
	assert( f != NULL && f(a) * f(b) < 0.0 && (b-a) > DBL_EPSILON); // (b-a) > DBL_EPSILON 即 b > a

	while( b - a > eps ) {
		m = (a + b)/2;
		if( f(m) * f(a) < 0.0 ) b = m;
		else a = m;
	}
	return m;
}

这个程序较为“好用”，只需给出函数f，区间[a, b]，误差eps即可。

迭代法

同样，有了对迭代法的理论基础，我们知道了迭代法的误差如何估计。下面是迭代法求一般方程的近似解的程序：

double iteration(double (*g)(double), double L, double x0, double eps)
{
	double x1, t = L/(1 - L);;
	for(;;) {
		x1 = g(x0);
		if(fabs( t*(x1-x0) ) < eps) 
			break;
		x0 = x1;
	}
	return x1;
}

这个函数没有上面的二分法那么好用，因为需要根据f(x)自行推出递推函数g，并根据递推函数的倒数找到一个常数L；再给出初值x0，误差eps。

割线法

事实上，真正通用的牛顿法很难实现，因为从f(x)推出它的导函数f1(x)的过程并不容易。割线法可以避免这一难题，它使用差商：

来代替牛顿公式中的导数f'(xk)，于是得到了“割线法”迭代公式：

割线法和牛顿法类似，有着明确的几何意义。下面的gif动态地展示了割线法的几何意义（若没有看到动画效果可尝试刷新本页）：

（图片来自Dr. Mathews的教案，）

割线法求一般方程的近似解的程序如下：

double secant(double (*f)(double), double x0, double x1, double eps)
{
	double x2;
	for(;;) {
		x2 = x1 - f(x1)/(f(x1) - f(x0))*(x1 - x0);
		if( fabs(x2-x1) < eps ) 
			break;
		x0 = x1;
		x1 = x2;
	}
	return x2;
}

这个函数也很好使用，只需给出f，[a, b]，eps即可。

割线法实现的sqrt如下：

double Sqrt(double A)
{
	double x0 = 0, x1 = A+0.25, x2;
	double fx0 = x0*x0 - A, fx1 = x1*x1 - A;
	
	for(;;) {
		x2 = x1 - fx1*(x1-x0) / (fx1-fx0);
		if(fabs(x2 - x1) < 2*DBL_EPSILON)
			break;
		x0 = x1; fx0 = fx1; 
		x1 = x2; fx1 = x2*x2 - A;
	}
	return x2;
}

收敛速度对比

对于sqrt的实现，本文介绍了三种方法，分别为：二分法，牛顿法，割线法；

二分法的收敛速度

对于二分法，相邻两次的误差ek+1和ek间的关系为：

，

由此，我们可以引申出迭代法收敛速度的判定标准：

---

定义  迭代法收敛的阶

设序列{xk}收敛于x*，并记ek = xk - x*，如果存在非负常数c和正常数p，使得

则称序列{xk}是p阶收敛的。当p=1，且0<|c|<1时，称为线性收敛；当p>1时，称超线性收敛，特别是p=2时，称平方收敛。

---

由收敛阶的定义可知，二分法是线性收敛的。

牛顿法的收敛速度

要确定牛顿法收敛的阶，需要经过一番推导，限于篇幅，这里直接给出结论：

当x*是f(x)=0的单根（回顾一下二次方程）时，牛顿法至少是二阶收敛的；

当x*是f(x)=0的重根时，牛顿法至少是一阶收敛的。

割线法的收敛速度

分析割线法收敛的阶同样不易，它比牛顿法略慢一些；有知道的同学可以告诉我；

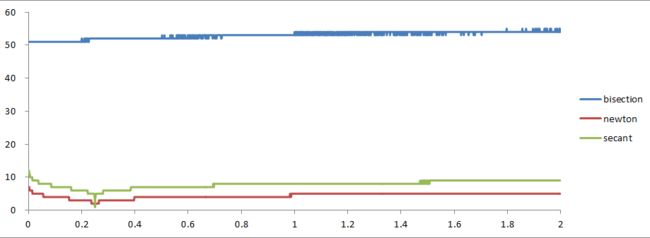
实验对比

下面通过实验对比几种方法的收敛速度。实验以不同版本的sqrt求出最终值所用的迭代次数为收敛速度的标准。

实验程序如下：

#include  // for fabs sqrt
#include  // for DBL_EPSILON DBL_DIG etc.
#include  // for clock
#include 
#include 

int iterateCount = 0;
double BisectionSqrt(double A)
{
	double a = 0.0, b = A + 0.25, m;
	
	for(;;){
		m = (b + a)/2;
		++iterateCount; // count iterate.
		// printf("  %.15f\n", m);
		if( m-a < DBL_EPSILON || b-m < DBL_EPSILON ) break; 
		if( (m*m - A) * (a*a - A) < 0.0 ) b = m;
		else a = m;
	}
	return m;
}

double NewtonSqrt(double A)
{
	double x0 = A + 0.25, x1, xx;
	for(;;) {
		x1 = (x0*x0 + A) / (2*x0);
		++iterateCount; // count iterate.
		// printf("  %.15f\n", m);
		if(fabs(x1 - x0) <= DBL_EPSILON) break;
		if(xx == x1) return x0; // break two value cycle.
		xx = x0;
		x0 = x1;
	}

	return x1;
}

double SecantSqrt(double A)
{
	double x0 = 0, x1 = A+0.25, x2;
	double fx0 = x0*x0 - A, fx1 = x1*x1 - A;
	
	for(;;) {
		x2 = x1 - fx1*(x1-x0) / (fx1-fx0);
		++iterateCount; // count iterate.
		// printf("  %.15f\n", x2);
		if(fabs(x2 - x1) < 2*DBL_EPSILON)
			break;
		x0 = x1; fx0 = fx1; 
		x1 = x2; fx1 = x2*x2 - A;
	}
	return x2;
}

int main()
{
#ifdef F_INFO
	puts("local machine floating point informations:");
	printf("FLT_DIG: %d, %g\n", FLT_DIG, FLT_EPSILON);
	printf("LDBL_DIG: %d, %g\n", DBL_DIG, DBL_EPSILON);
	printf("LDBL_DIG: %d, %g\n", LDBL_DIG, LDBL_EPSILON);
#endif

	double x, res, stdres;
	
	while( scanf("%lf", &x) == 1 )
	{
		stdres = sqrt(x);
		printf("%15g ", x);
		
		iterateCount = 0;
		res = BisectionSqrt(x);
		printf("%14g\t%3d\t", res-stdres, iterateCount); 
		
		iterateCount = 0;
		res = NewtonSqrt(x);
		printf("%14g\t%3d\t", res-stdres, iterateCount); 
		
		iterateCount = 0;
		res = SecantSqrt(x);
		printf("%14g\t%3d\t", res-stdres, iterateCount); 
		
		printf("\n");
	}
	
	return 0;
}

程序输出\t是为了方便重定位到文本文件后，粘贴到excel等表格软件中；格式串是为了方便控制台查看；

测试数据由下面的python脚本生成：

for x in range(1, 10000):
	print x*0.01
	
for x in range(10000, 90000):
	print x
	
for x in range(1000000, 9000000, 37):
	print x

for x in range(100000000, 10000000000, 2311):
	print x

可以通过管道进行测试：

gcc sqrt_cmp.c -o sqrt_cmp # 编译
python inputgen_sqrt_cmp.py | sqrt_cmp # 测试

经过如下数据试验：

delta = 0.05
count = 1/delta
for x in range(1, 2*int(count)):
	print x*delta

得到的迭代次数随x的变化关系如下图所示：

图中，很坐标表示x值，纵坐标表示迭代次数。

试验结果表明：牛顿法的收敛速度最快（迭代次数少），割线法次之，而二分法收敛最慢。

总结

本文分别描述了二分法、牛顿法、割线法，等几种求方程近似解算法的步骤及实现；另外，从理论方面解释了这些算法步骤背后数学原理；并将这些方法进行了一般化的推广。最后，本文针对不同方法实现的sqrt进行了实验对比。实验结果表明：牛顿法的收敛速度快于割线法，割线法快于二分法。