基于Matlab的极限学习机(ELM)实现
最近打算做一些参数预测相关内容,选基学习器的时候注意到了极限学习机。
极限学习机简介
极限学习机(Extreme Learning Machine, ELM)最早于2004年由南洋理工大学的Guang-Bin Huang、Qin-Yu Zhu和Chee-Kheong Siew提出,并发表于当年的IEEE国际交互会议(IEEE International Joint Conference)中,目的是为了对反向传播算法(Backward Propagation, BP)进行改进以提升学习效率低并简化学习参数的设定。ELM是一类基于前馈神经网络(Feedforward Neuron Network, FNN)构建的机器学习方法,适用于监督学习和非监督学习问题,其特点是隐含层节点的权重为随机或人为给定的,且不需要更新,学习过程仅计算输出权重。因此在实际使用时ELM的训练速度比传统BP网络快很多。
极限学习机的Matlab实现
由于极限学习机已经提出很多年了,因此网络上能找到很多公开的实现代码或工具包。对比了若干代码及工具包之后,最终选择GitHub - ELM_MatlabClass作为测试工具包。这个工具包包含了基本的极限学习机代码,可用于实现分类问题和回归问题。其中ELM_MatlabClass.m为极限学习机实现,computeAccuracy.m和computeR2.m可用于计算训练和测试的准确度,example_CLASSIFICATION.m提供了分类问题的示例,example_REGRESSION.m提供了回归问题的示例。
% 回归问题示例
% 数据读取及预处理
data = csvread('data_akbilgic.csv',1,1);
[nPatterns, nInputs] = size(data);
% 最后一列为待预测参数
nInputs = nInputs - 1;
% 归一化至 -1~1
for i = 1 : (nInputs + 1)
data(:,i) = -1 + 2.*(data(:,i) - min(data(:,i)))./(max(data(:,i)) - min(data(:,i)));
end
% 数据集划分,前60%为训练集,后40%为测试集
percTraining = 0.6;
endTraining = ceil(percTraining * nPatterns);
trainData = data(1:endTraining,:);
validData = data(endTraining+1:end,:);
% 隐层数目
nHidden = 10;
% 建立模型
ELM = ELM_MatlabClass('REGRESSION',nInputs,nHidden);
% 训练模型
ELM = train(ELM,trainData);
% 进行预测
Yhat = predict(ELM,trainData(:,1:end-1));
fprintf('TRAINING RSquared = %3.3f\n',computeR2(trainData(:,end),Yhat));
% 计算准确度
Yhat = predict(ELM,validData(:,1:end-1));
fprintf('VALIDATION RSquared = %3.3f\n',computeR2(validData(:,end),Yhat));
%% 灵敏度分析,可确定最佳隐层数目,范围1~100
nHidden = 1:100;
trainR2 = zeros(size(nHidden));
validR2 = zeros(size(nHidden));
for i = 1 : numel(nHidden)
ELM = ELM_MatlabClass('REGRESSION',nInputs,nHidden(i));
ELM = train(ELM,trainData);
Yhat = predict(ELM,trainData(:,1:end-1));
trainR2(i) = computeR2(trainData(:,end),Yhat);
Yhat = predict(ELM,validData(:,1:end-1));
validR2(i) = computeR2(validData(:,end),Yhat);
end
% 显示曲线图
plot(nHidden,[trainR2;validR2],'-o');
xlabel('Number of Hidden Neurons');
ylabel('RSquared');
legend({'training','validation'},'Location','southeast')
回归问题测试
为了测试极限学习机针对回归问题的预测效果,决定用其他数据集对其进行测试。选择了nasa公开的c-mapss发动机性能退化数据集,使用train_FD002.txt中unit2的发动机数据,删除部分受发动机循环数影响不大的参数,最终保留参数2,3,4,7,8,9,11,12,13,14,15,17,20,21,其中参数8(风扇转速)为被预测量。本次循环共有269组数据,取前162组作为训练集,后107组作为测试集。预测结果如下:
TRAINING RSquared = 0.999
VALIDATION RSquared = 0.998
预测相对误差如下:
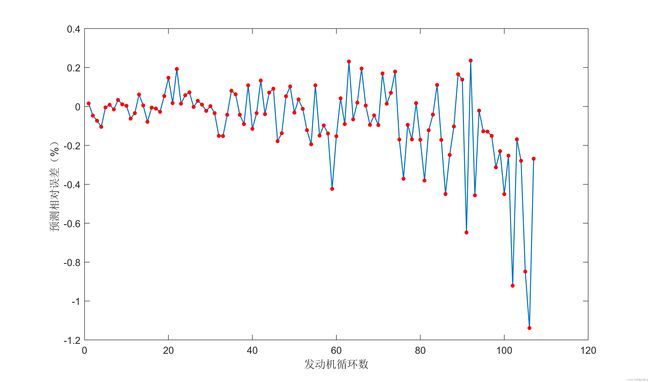
可以看到由于数据集较简单,且所选择参数之间相关性较强,因此预测效果较好。在数据集复杂或参数之间相关性不明显时,使用单一学习算法效果可能较差,这种情况下可以考虑使用集成学习或多种方法融合来提升预测精确度。