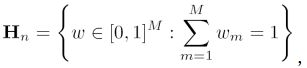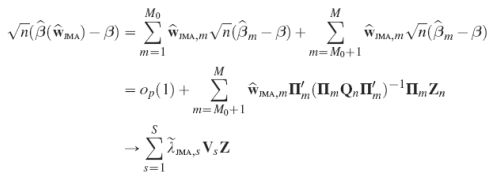智源青年科学家张新雨：从模型平均到集成学习、迁移学习

2020年2月11日上午，在 “智源论坛Live | 青年科学家线上报告会”中，智源青年科学家、中科院系统所研究员张新雨做了题为《模型平均、集成学习与迁移学习》的主题演讲。

张新雨，中科院系统所博士，曾在美国德克萨斯A&M大学做博士后研究。主要研究方向包括模型平均、模型选择和组合预测等，取得了一系列获得国际同行好评的重要成果。国家杰青、优青。曾获中国科学院优秀博士学位论文。代表作有《Focused Information Criterion and Model Averaging for Generalized Additive Partial Linear Models》（AoS 2011）等。

 

模型平均是统计学的前沿研究领域，旨在处理模型不确定性，通常比采用单个模型能得到更好的预测效果。张新雨在演讲中细致解析了模型平均的概念内涵和理论难点，并展望了它应用于AI集成学习、迁移学习研究的几个重要方向和挑战，可谓干货十足，为我们了解模型平均理论在人工智能算法领域的应用和趋势提供了一个系统清晰的知识技术进阶图谱。

 

下面，是张新雨分享的精彩要点。

整理：钱小鹅

 研究基础：模型平均和集成学习的概念内涵

首先，我们来介绍研究基础中贯穿始终的两个概念：

模型平均方法(Model Averaging/Model Aggregation/Model Ensembles)是当今国际统计学和计量经济学研究的热点之一，具有十分广泛的应用价值，最近十几年已取得重要进展，其原理可以理解为：假设有S个模型（或者S种估计方法），每个模型（或方法）得出了一个预测值，我们不妨将其写为：

，

那么模型平均方法得到的最终估计值为：

我们从公式中不难看出，模型的平均中包含了权重，该权重是数据依赖的。模型平均方法是处理模型不确定性和提高预测效果的方法，其核心研究内容是权重的选择以及不确定性的衡量。

集成学习(Ensemble Learning) 是使用多种学习器进行学习，并使用某种规则把各个学习结果进行集成从而获得比单个学习器更好的学习效果的一种机器学习方法，它可以用于分类问题集成、回归问题集成等。

从上述描述的两个概念，我们不难看出，模型平均实质也是一类集成学习方法。

 

张新雨在过去的工作中，主要的贡献也集中在模型平均方法和集成学习两个领域，他重点为我们介绍了三个比较突出的贡献：

• 解决了模型平均研究领域的难题

• 针对复杂数据类型提出了模型平均方法

• 建立了多模型统计推断的理论基础

我们分别来进行说明。

1. 解决了模型平均研究领域的难题

我们不妨假设

其中为不同的模型得到的结果，为误差项，根据上文中模型平均估计公式为：

我们定义损失函数为：

权重选择方式定义为：

我们定义渐近最优性：

张新雨及其团队成员的主要贡献在于，将原有的离散权重

扩展为连续权重

原有理论主要的应用范围为嵌套结构，即模型必须逐渐增大，扩展后不再只应用于嵌套模型，它可以应用于所有满足上述连续权重的所有模型。

2. 针对复杂数据类型提出了模型平均方法

目前数据类型越来越复杂，所谓“复杂”是指数据非独立同分布，其中包括：区间时序数据（比如股市、油价等）、空间数据（比如疫情和区域的的关系）、时空数据、函数型数据（比如交通监控，是一个实时的流数据）。在这一方面，张新雨主要分享给大家两个成果：

• 最优化：通过权重选择方法，模型的预测风险与最优风险的比值是趋于1的。

• 适应性：通过权重选择方法，模型的预测风险有上确界，该上确界是适应性的，因为在上确界的表达式由最优单模型预测风险决定。

图1: 最优性及适应性的理论成果

3. 建立了多模型统计推断的理论基础

这是模型平均领域的新内容，它不同于传统的机器学习方法：传统的机器学习方法只关注预测的结果，但是多模型统计推断的理论不但关注预测结果，同时也关注结果的不确定性。研究初期，张新雨首先将重点集中在固定维度方向，利用极限分布给出了不确定性的衡量，得出的结论如下：

最近，他将该工作发展到了高维情况，在高维情况下发现不确定的衡量同时也可以达到模型选择的效果，其结论如下【1】：

关于多模型统计的工作，除了张新雨为我们分享的成果之外，还有不少比较优秀的成果，比如：两位诺奖的获得者T. Sargen、L. Hansen，更多的是从贝叶斯估计出发去分析问题【2】；图2中提及的书，引用量达到4万多次，是从频率的角度分析问题；2008年挪威科学与文学院院士N. Hjort等人的著作《Model Selection and Model Averaging》以及2018年Springer的刊物《Model Averaging》，感兴趣的同学可以阅读研究。

图2: 多模型统计推理的优秀著作介绍

拟研究内容：模型平均应用于集成学习、迁移学习的主要方向 

在拟研究内容中，张新雨从三个方面为大家介绍：稳健的集成学习、基于微分方程的集成学习以及多源域下参数迁移学习，下面我们将分别为大家详细介绍三方面的成果。

 

1. 稳健集成学习

目前，利用模型平均方法做集成学习已经有一些比较优秀的工作，比如：如图3推荐的一篇综述性的文章，该文章主要讲解使用频率型模型平均方法来进行模型的集成；如图4，作者使用贝叶斯模型平均将Takagi-Sugeno Fuzzy Logic (TS-FL)、Artificial Neural Network (ANN)、以及Neuro-Fuzzy (NF) 三个模型预测的结果进行模型平均，得到了较三种单模型预测结果更好的结果。

图3:使用频率方法进行模型平均

图4: 贝叶斯方法进行模型平均

目前，稳健学习是模型平均领域研究中非常关注的问题，即：如果机器学习本身的输入结果带有干扰，如何进行具有抗干扰能力的平均预测。我们给出如下公式：

其中η为干扰数值。上述公式表示如果我们将模型的干扰项控制在的范围∈内，可以使用上述公式来估计具有抗干扰能力的参数θ。目前在该领域张新雨拟研究的内容包括：

• 考虑组合多种学习器进一步提高学习效果；

• 考虑复杂数据建模时候的模型不确定性，例如时序数据、缺失数据等。

2. 基于微分方程的集成学习

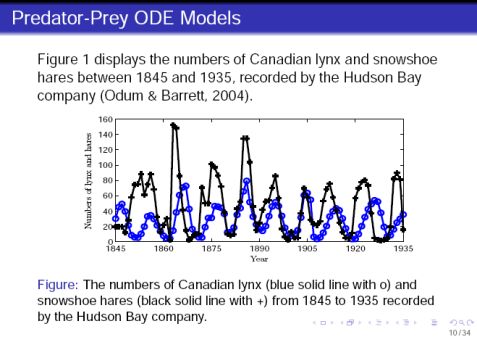
首先我们补充一些关于微分方程估计的研究基础。我们先简单看一个例子：图5中给出了捕食和被捕食的数据模型

图5：捕食和被捕食者的数据模型

目前有很多微分方程模型来刻画图5的数据，如图6:

图6:捕食和被捕食者的微分方程模型

其中H是捕食者的数量，P为被捕食者的数量。上述的微分方程模型可以被总结抽象出如图7中微分方程：

图7:估算微分方程的参数

与已有的参数估计所不同的是，X(t)并非都是可以准确观测到的，因此该数据量中将会携带随机的误差，因此随机的建模将会对结果起到很好的作用。张新雨为我们详细讲解了此类带有误差的微分方程的估计方式，具体过程如下：

正如上文图6中提到，捕食和被捕食者的数据可以通过至少四种不同的微分模型刻画，那么如何选择微分模型呢？张新雨在这个问题上做了相关的研究，并取得了一些成果。他提出了基于最小二乘近似的模型选择方法，通过该方法选择出的模型与真实模型相等的概率是趋于1的【3】。本节中涉及的内容参考文献为[3]，感兴趣的读者可以阅读原文进行研究。

张新雨为我们分享的第二个实例为SEIR传染病模型的集成学习理论，模型如下：

其中S代表易感人群、E代表潜伏人群、I代表确诊人群、R代表治愈人群，其他为待估参数。上述问题中也存在观测数据中包含噪声的情况，比如有些确诊的患者没有被发现。那么我们应该选择哪种模型来进行最终的预测，也可以使用上述文献中给出的算法进行选择。

 

3. 多源域下参数迁移学习

首先，我们来介绍两个概念：

迁移学习（Transfer Learning）：是一种机器学习方法，它将一个领域（称为源域）的知识，迁移到另一个领域（称为目标域），使得目标域能够取得更好的预测效果；

参数迁移学习：是指目标领域与源领域之间共享相同的模型参数或者是服从相同的先验分布情形下的迁移学习，它是重要的迁移学习类型。

在参数迁移学习中，有时源域可能不止一个，如何综合集成多个源数据下的学习结果是关键的步骤。因此，本方向张新雨为我们分享的具体的研究目标为在多个源域下提出最优或者近似最优的参数迁移学习方法，并建立其统计学理论基础。研究内容包括三类：

• 基于传统统计模型的多源域下参数迁移学习方法的研究；

• 基于复杂数据类型的多源域下参数迁移学习方法的研究；

• 基于其他机器学习算法的多源域下参数迁移学习方法的研究。

该部分，张新雨为我们主要分享了第一类---基于传统统计模型的多源域下参数迁移学习方法的研究，为说明方便，我们不妨先给出参数说明，如下图8所示：

图8:多模型的参数说明

其中X、Z为输入变量，f为模型的数据产生过程，α、β、γ为模型参数，其中不难看β出为共享参数，我们考虑其中一个模型为主模型，其他模型为辅助模型，我们的目标是：给定X、Z，如何利用辅助模型，对结果进行预测。关于上述的模型我们不妨给大家简单举例说明：假设Y表示是否发生心脏病，β表示多个实验室采集的血压对结果的影响（共享参数），其他参数为非共享参数，表示不同实验室采集的数据Z的影响不尽相同，此时，我们可以利用该方法对Y进行预测。常用的方法是直接利用主模型求解；第二类方法我们可以考虑有约束的极大似然估计（注意：第二类方法的前提是所有的模型都必须是正确的）；第三类方法是模型平均法，这类方法的优势在于即使辅助模型中包含差模型甚至错误模型，我们仍然可以通过权重的选择来降低这些差的或者错误的模型对预测结果的影响。该方法分为六个步骤：

1.针对每个模型进行参数α、β、γ估计；

2.选择主模型作为模型，β为其他模型参数，α、γ为主模型参数，预测Y；

3.对来自各个模型的预测值进行加权；

4.建立针对主模型预测的交叉验证方法权重选择准则；

5.将交叉验证准则进行极小化得到权重；

6.将得到权重带回到第3步得到集成学习的预测。

该方法的优势在于：整个过程中计算复杂度是非常低的，同时由于模型之间只有参数需要在整个过程中暴露出来，不同的模型本身的估算过程可以独立进行，因此极大的解决了数据保密性等问题，同时在大规模计算中也更容易构造并行结构。同时，张新雨为我们介绍了该方法的一些非常好的性质：

1.如果主模型误设定（主模型不是完全正确的），并且数据足够充分，该方法可以极小化预测风险，也就是具有预测的最优性；

2.如果主模型本身就是正确的，并且错误模型的风险不能太小，该方法学习到的权重将是正确模型的权重和为1，其余模型权重为0。

该算法同样适用于大数据的实例中。

 

结语

本次智源青年科学家候选人公开报告中，张新雨为我们深入浅出的分享了他已有的研究成果以及对模型平均方法领域未来的一些研究设想，智源社区编辑整理了部分核心观点，欢迎将你的读后感告诉我们，对该领域感兴趣的同学亦可继续阅读文中为大家推荐的书籍和论文。

 

参考文献

[1] Zhang, X., Zou, G., Liang, H. and Carroll, R. (in press). Parsimonious Model Averaging with a Diverging Number of Parameters. Journal of the American Statistical Association. https://doi.org/10.1080/01621459.2019.1604363

[2] Hansen, L. P. (2014). Nobel lecture: Uncertainty outside and inside economic models. Journal of Political Economy, 122, 945-987.

[3]Zhang, X., Cao, J. and Carroll, R.J. (2015). On the Selection of Ordinary Differential Equation Models with Application to Predator-prey Dynamical Models. Biometrics, 71, 131-138.