机器学习——Logistic回归

一、定义

Logistic回归是一种广义线性回归（generalized linear model），因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 w’x+b，其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w’x+b作为因变量，即y =w’x+b，而logistic回归则通过函数L将w’x+b对应一个隐状态p，p =L(w’x+b),然后根据p 与1-p的大小决定因变量的值。逻辑回归假设数据服从伯努利分布，通过极大似然估计的方法，运用梯度下降来求解参数，来达到数据二分类的目的。

• 回归：假设现在有一些数据点，我们用一条直线对这些点进行拟合（该直线称为最佳拟合直线），这个拟合的过程就称为回归。
• 主要思想：根据现有数据对分类边界线建立回归公式，以此进行分类。
  逻辑回归的一般过程： 
  - 收集数据：采用任意方法收集数据。
  - 准备数据：由于需要进行距离计算，因此要求数据类型为数值型。另外，结构化数据格式则最佳。
  - 分析数据：采用任意方法对数据进行分析。
  - 训练算法：目的是为了找到最佳的分类回归系数。
  - 测试算法
  - 使用算法

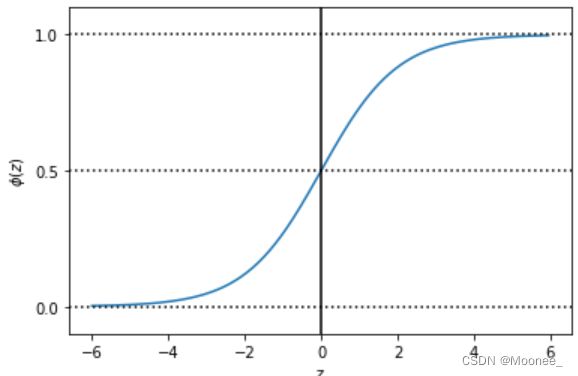
二、Sigmoid函数

若要处理的是二分类问题，我们期望的函数输出会是0或1，类似于单位阶跃函数，可是该函数是不连续的，不连续不可微。

因此我们换用Sigmoid函数，当x=0时，y为0；随着x的增大，y值趋近于1，随着x的减小，y趋近于0，当横坐标足够大时，Sigmoid函数就会看起来像一个阶跃函数。
　

• python绘制Sigmoid图像：

import matplotlib.pyplot as plt
import numpy as np
 
def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))
 
z=np.arange(-6,6,0.05)
plt.plot(z,sigmoid(z))
plt.axvline(0.0,color='k')
plt.axhline(y=0.0,ls='dotted',color='k')
plt.axhline(y=1.0,ls='dotted',color='k')
plt.axhline(y=0.5,ls='dotted',color='k')
plt.yticks([0.0,0.5,1.0])
plt.ylim(-0.1,1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
plt.show()

三、梯度上升算法

训练算法时采用了梯度上升算法，其思想是：要找到某函数的最大值，最好的方法就是沿着该函数的梯度方向探寻。如果梯度记为∇，则函数f(x,y)的梯度由 下式表示：

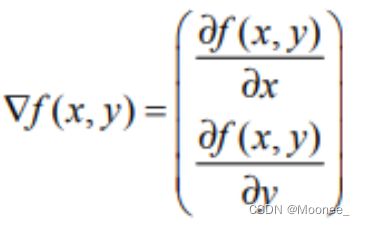
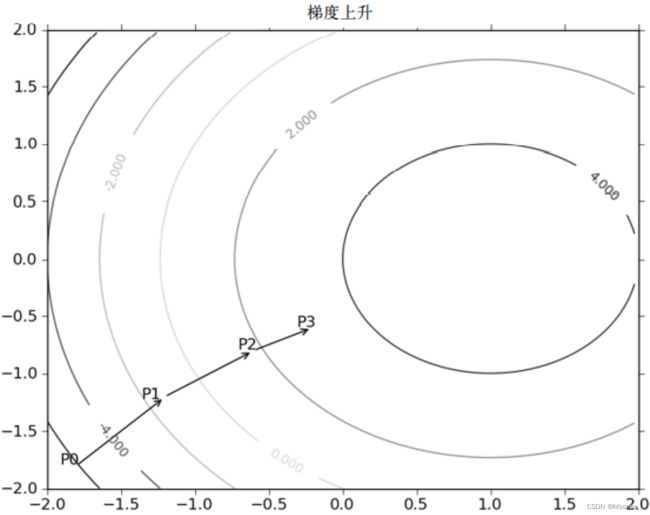
　　如图，梯度上升算法到达每个点后都会重新估计移动的方向。从P0开始，计算完该点的梯度，函数就根据梯度移动到下一点P1。在P1点，梯度再次被重新计算，并沿新的梯度方向移动到P2。如此循环迭代，直到满足停止条件。迭代的过程中，梯度算子总是保证我们能选取到最佳的移动方向。
　　

• python绘制结果：

#逻辑斯蒂分类算法  
import numpy as np  

#画图的函数  
from matplotlib.colors import ListedColormap  
import matplotlib.pyplot as plt  
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):  
  
    # setup marker generator and color map  
    markers = ('s', 'x', 'o', '^', 'v')  
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')  
    cmap = ListedColormap(colors[:len(np.unique(y))])#通过ListedColormap来定义一些颜色和标记号，并通过颜色列表生成了颜色示例图  
    # plot the decision surface  
    #对两个特征的最大值最小值做了限定（使用两个特征来训练感知器）  
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1  
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1  
    #利用meshgrid函数，将最大值、最小值向量生成二维数组xx1和xx2  
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))  
    #创建一个与数据训练集中列数相同的矩阵，以预测多维数组中所有对应点的类标z  
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)  
    Z = Z.reshape(xx1.shape)#将z变换为与xx1和xx2相同维度  
    #使用contourf函数，对于网格数组中每个预测的类以不同的颜色绘制出预测得到的决策区域  
    plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)  
    plt.xlim(xx1.min(), xx1.max())  
    plt.ylim(xx2.min(), xx2.max())  
  
    for idx, cl in enumerate(np.unique(y)):  
        plt.scatter(x=X[y == cl, 0],   
                    y=X[y == cl, 1],  
                    alpha=0.8,   
                    c=colors[idx],  
                    marker=markers[idx],   
                    label=cl,   
                    edgecolor='black')  
  
    # highlight test samples  
    if test_idx:  
        # plot all samples  
        X_test, y_test = X[test_idx, :], y[test_idx]  
  
        plt.scatter(X_test[:, 0],  
                    X_test[:, 1],  
                    c='',  
                    edgecolor='black',  
                    alpha=1.0,  
                    linewidth=1,  
                    marker='o',  
                    s=100,   
                    label='test set')  

#训练集与测试集的获取,采用鸢尾花数据集  
from sklearn import datasets  
iris=datasets.load_iris()  
x=iris.data[:,[2,3]]  
y=iris.target  
  
#对数据集进行划分  
from sklearn.model_selection import train_test_split
#采用scikit-learn中的cross_validation模块中的train_test_split（）函数，随机将iris数据特征矩阵x与类标向量y按照3:7划分为测试数据集和训练数据集  
x_train,x_test, y_train, y_test =train_test_split(x,y,test_size=0.3, random_state=0)  
  
#为了优化性能，对特征进行标准化处理  
from sklearn.preprocessing import StandardScaler  
sc=StandardScaler()  
sc.fit(x_train)#通过fit方法，可以计算训练数据中每个特征的样本均值和方差  
x_train_std=sc.transform(x_train)#通过调用transform方法，可以使用前面获得的样本均值和方差来对数据做标准化处理  
x_test_std=sc.transform(x_test)  

from sklearn.linear_model import LogisticRegression
lr=LogisticRegression(C=1000.0,random_state=0)
lr.fit(x_train_std,y_train)
print("Training Score:%f"%lr.score(x_train_std,y_train))#返回在(X_train,y_train)上的准确率  
print("Testing Score:%f"%lr.score(x_test_std,y_test))#返回在(X_test,y_test)上的准确率  
  
x_combined_std = np.vstack((x_train_std, x_test_std))#将数组垂直排列成多个子数组的列表。  
y_combined = np.hstack((y_train, y_test))# 按水平顺序（列）顺序堆栈数组。  
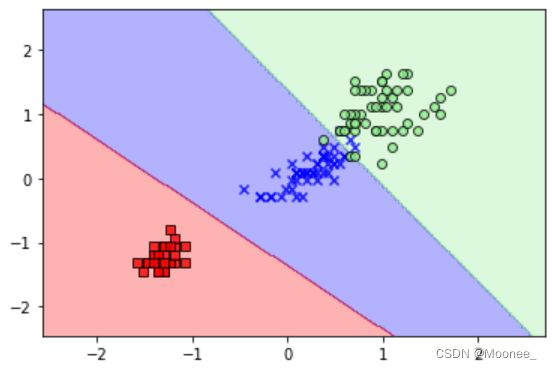
plot_decision_regions(X=x_combined_std, y=y_combined, classifier=lr, test_idx=range(105, 150))  
plt.xlabel('petal length [standardized]')  
plt.ylabel('petal width [standardized]')  
plt.legend(loc='upper left')  
plt.show()

• 梯度下降算法 梯度下降算法，它与这里的梯度上升算法是一样的，只是公式中的加法需要变成减法。因此，对应的公式可以写成：
  梯度上升算法用来求函数的最大值，而梯度下降算法用来求函数的最小值。

四、Logistic回归的优缺点

优点：计算代价不高，易于理解和实现

缺点：容易欠拟合，分类精度可能不高

适用数据类型：数值型和标称型数据

五、python实现分类器的应用

下图所示为数据集test.txt：

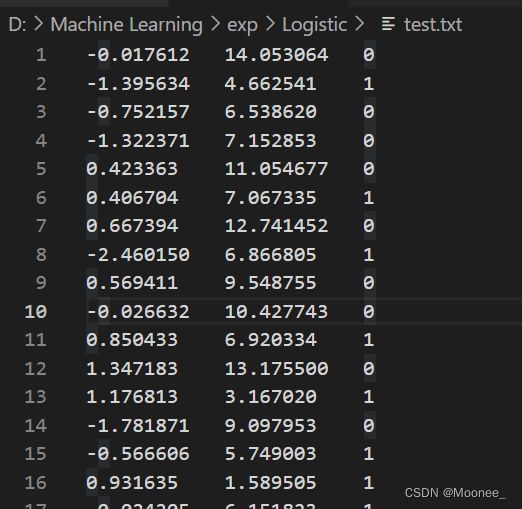
数据集有100个样本点，每个点包含两个数值型特征：X1和X2。

在此数据集上，我们将通过使用梯度上升法找到最佳回归系数，也就是拟合出Logistic回归模型的最佳参数。

梯度上升法的伪代码如下：

每个回归系数初始化为1
重复R次：
    计算整个数据集的梯度
    使用alpha*gradient更新回归系数的向量
返回回归系数

①求出回归系数[w0,w1,w2]

# 加载数据集
def loadDataSet():
    dataMat = []                                                      # 数据列表
    labelMat = []                                                     # 标签列表
    fr = open('test.txt')                                          # 打开文件
    for line in fr.readlines():                                       # 遍历每行，读取数据
        lineArr = line.strip().split()                                # 去除回车符
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])   # 把此行的数据添加到数据列表里面
        labelMat.append(int(lineArr[2]))                              # 添加标签进列表
    return dataMat, labelMat
# sigmoid函数
def sigmoid(inX):
    return 1.0 / (1 + exp(-inX))
# 梯度上升算法
def gradAscent(dataMatIn, classLabels):    
    dataMatrix = mat(dataMatIn)           
    labelMat = mat(classLabels).transpose()            
    m, n = shape(dataMatrix)   # 获取数据集矩阵的大小，m为行数，n为列数
    alpha = 0.001      # 步长
    maxCycles = 500      # 迭代次数
    weights = ones((n, 1))     # 权重初始化为1
    for k in range(maxCycles):     # 重复矩阵运算
        h = sigmoid(dataMatrix * weights)   
        error = (labelMat - h)      # 计算误差
        weights = weights + alpha * dataMatrix.transpose() * error 
    return weights
# 获得回归系数
dataMat, labelMat = loadDataSet()
weigths = gradAscent(dataMat, labelMat)
print("w0: %f, w1: %f, W2: %f" % (weigths[0], weigths[1], weigths[2]))

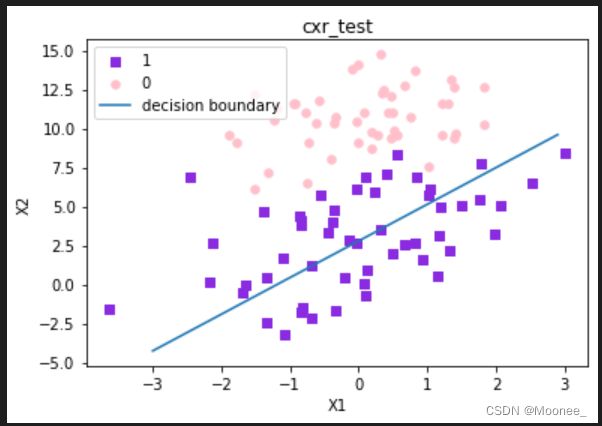
②分析数据，画出决策边界

# 绘制数据集和Logistic回归最佳拟合直线
def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()      
    dataArr = array(dataMat)      
    n = shape(dataArr)[0]     # 获取数据总数
    xcord1 = []; ycord1 = []       # 存放正样本
    xcord2 = []; ycord2 = []       # 存放负样本
    for i in range(n):                                     # 依据数据集的标签来对数据进行分类
        if int(labelMat[i]) == 1:                          # 数据的标签为1，表示为正样本
            xcord1.append(dataArr[i, 1]); ycord1.append(dataArr[i, 2])
        else:      
            xcord2.append(dataArr[i, 1]); ycord2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='blueviolet', marker='s')  # 绘制正样本
    ax.scatter(xcord2, ycord2, s=30, c='pink')      # 绘制负样本
    x = arange(-3.0, 3.0, 0.1)      
    y = (-weights[0] - weights[1] * x) / weights[2]    
    ax.plot(x, y)
    plt.title('cxr_test')          
    plt.xlabel('X1'); plt.ylabel('X2')
    　plt.legend(["1","0","decision boundary"]
    plt.show()
    dataMat, labelMat = loadDataSet()
    weigths = gradAscent(dataMat, labelMat)
    plotBestFit(weigths.getA())
    print("w0: %f, w1: %f, W2: %f" % (weigths[0], weigths[1], weigths[2]))

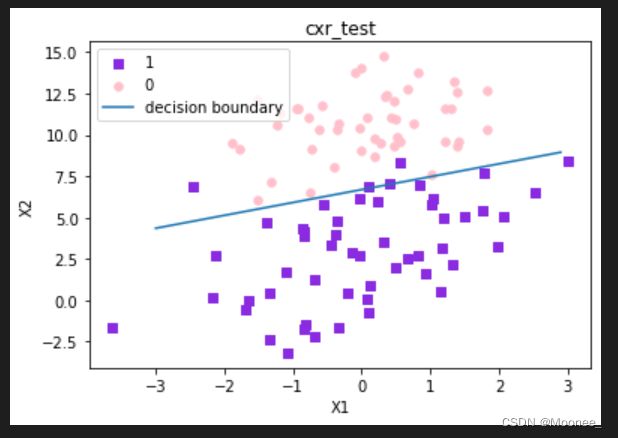
　　这个分类器分类效果不错，从图上看只分错了几个点而已，但是回顾对算法的原理的解析，我们却发现这个这个方法需要相当大量的计算，因此下一步我们将对其进行改进，从而使它可以运用在我们现实生活中，处理例子复杂数量大的数据集。

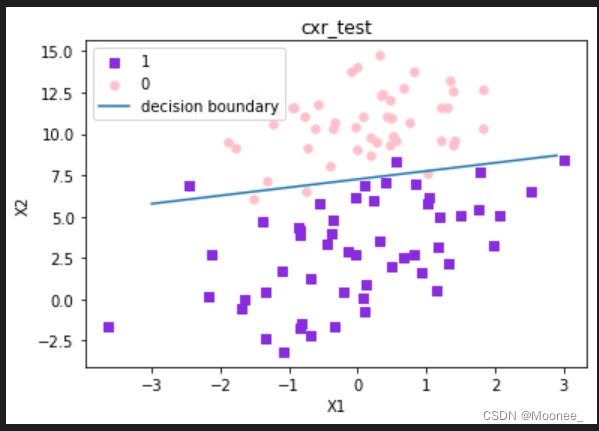
③训练算法：随机梯度上升

一种改进的方法是一次仅用一个样本点来更新回归系数，即随机梯度上升法。由于可以在新样本到来时对分类器进行增量式更新，因此随机梯度上升法是一个在线学习算法。
随机梯度上升法可以写成如下伪代码：

所有回归系数初始化为1
对数据集中每个样本
        计算该样本的梯度
　　    使用alpha*gradient更新回顾系数值
 返回回归系数值

• 随机梯度上升和梯度上升法在代码上的区别：

（1）后者的变量h和误差error都是向量。
（2）前者没有矩阵的转换过程，所有变量的数据类型都是Numpy数组。

def stocGradAscent0(dataMatrix, classLabels):   
    m, n = shape(dataMatrix)  
    alpha = 0.01     #步长
    weights = ones(n)     #初始化为1
    for i in range(m):    # 重复矩阵运算
        h = sigmoid(sum(dataMatrix[i] * weights))   
        error = classLabels[i] - h     # 计算误差
        weights = weights + alpha * error * dataMatrix[i]     #更新权重
    return weights
    
    dataMat, labelMat = loadDataSet()
    weigths = stocGradAscent0(array(dataMat), labelMat)
    plotBestFit(weigths)

拟合曲线错了三分之一的样本，要进行改进。

④改进随机梯度上升

判断优化算法的优劣的可靠方法是看它是否收敛，也就是看参数是否稳定。

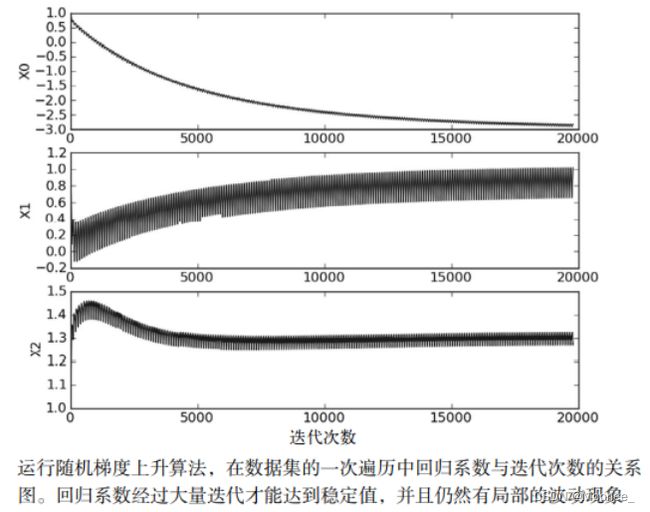
由上图可知，x2只经过50次迭代就达到了稳定值，但其他两个需要更多次迭代。

• 有三点改进：
  （1）alpha每次迭代的时候都会调整。不会减小到0，满足某个条件时也不是严格下降的。
  （2）随机选取样本来更新回归系数，这种做法会减少周期性波动。
  （3）增加了迭代参数的设置。默认为150次，如果给定，将会按照新的参数值进行迭代。

对此进行改进的随机梯度上升算法的代码如下：

def stocGradAscent1(dataMatrix, classLabels, numIter=150):  
    m, n = shape(dataMatrix)           
    weights = ones(n)              
    for j in range(numIter):
        dataIndex = list(range(m))                 
        for i in range(m):
            alpha = 4 / (1.0 + j + i) + 0.0001           
            randIndex = int(random.uniform(0, len(dataIndex)))  
            h = sigmoid(sum(dataMatrix[randIndex] * weights))  
            error = classLabels[randIndex] - h          
            weights = weights + alpha * error * dataMatrix[randIndex]  
            del (dataIndex[randIndex])          
    return weights

    dataMat, labelMat = loadDataSet()
    weigths = stocGradAscent1(array(dataMat), labelMat)
    plotBestFit(weigths)

效果很好，而且计算量少。

改进后的回归系数和迭代次数的关系图：

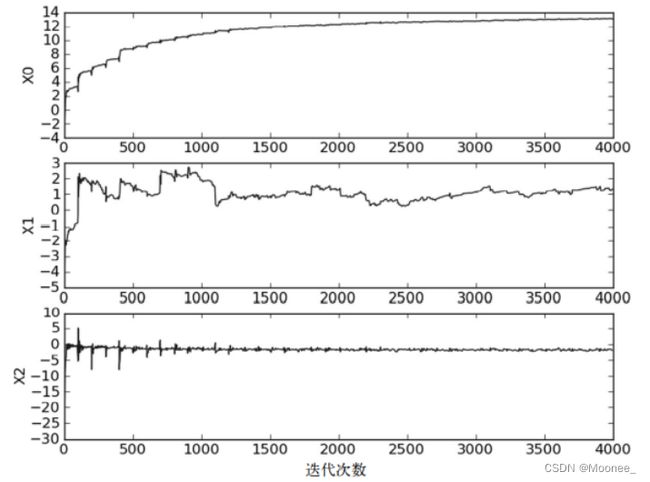
可以发现：
　　（1）此关系图中系数没有之前的迭代次数图那样出现周期性的波动。
　　（2）水平轴比之前的图短了很多。

六、实例：从疝气病症状预测病马的死亡率

①准备数据，处理数据中的缺失值

流程：
　　（1）收集数据：给定数据文件。
　　（2）准备数据：用python解析文本文件，并填充缺失值。
　　（3）分析数据：可视化并观察数据。
　　（4）训练算法：使用优化算法，找到最佳系数。
　　（5）测试算法：为了量化回归的效果，需要观察错误率，根据错误率决定是否退到训练阶段，通过改变迭代的次数和步长等参数来得到更好的回归系数。

数据包含了368个样本和28个特征。

疝气病是描述马胃肠痛的术语。这种病不一定源自马的肠胃问题，其他问题也可能引发马疝病。

该数据集中包含了医院检测马疝病的一些指标，有的指标比较主观，有的指标难以测量，例如马的疼痛级别。
　

预处理数据阶段需要做两件事：
（1）所有的缺失值必须用一个实数值来替换，因为使用的NumPy数据类型不允许包含缺失值。这里选择实数0来替换所有缺失值，恰好能适用于Logistic回归。

回归系数的更新公式：

weights = weights + alpha * error * dataMatrix[randIndex]

如果说dataMatrix的某特征对应值是0，那么该特征的系数将不做更新，即：

weights = weights

由于sigmoid(0)=0.5，即它对结果的预测不惧任何倾向性，因此不会对误差造成任何影响。

（2）如果在测试数据集中发现了一条数据的类别标记已经缺失，那么简单的做法就是将该条数据丢弃。

②训练算法，使用优化算法，找到最佳系数

from numpy import *

def sigmoid(inX):
    return 1.0/(1+exp(-inX))

def stoGradAscent1(dataMatrix, classLabels, numIter = 150):
    m,n = shape(dataMatrix)
    weights = ones(n)
    for j in range (numIter):
        dataIndex = range(m)
        for i in range(m):
            alpha = 4 / (1.0 + j + i) + 0.01
            randIndex = int(random.uniform(0, len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex] * weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del (list(dataIndex)[randIndex])
    return weights

③测试算法，用Logistic回归进行分类

def classifyVector(inX, weights):
    prob = sigmoid(sum(inX * weights))
    #大于0.5 返回 1；否则返回0
    if prob > 0.5:
        return 1.0
    else:
        return 0.0

def colicTest():
    frTrain = open('HorseColicTraining.txt')
    frTest = open('HorseColicTest.txt')
    trainingSet = []
    trainingLabels = []
    
    for line in frTrain.readlines():
        currLine = line.strip().split('\t') #分割
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        #存入训练样本特征
        trainingSet.append(lineArr)
        #存入训练样本标签
        trainingLabels.append(float(currLine[21]))
    #使用改进后的随机梯度下降算法得到回归系数
    trainingWeights = stoGradAscent1(array(trainingSet), trainingLabels, 500)

    #统计测试集预测错误样本数量和样本总数
    errorCount = 0
    numTestVec = 0.0
    for line in frTest.readlines():
        #循环一次，样本数加1
        numTestVec += 1.0
        currLine = line.strip().split('\t') #分割
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        
        # 利用分类预测函数对该样本进行预测，并与样本标签进行比较
        if int(classifyVector(array(lineArr), trainingWeights)) != int(currLine[21]):
            errorCount += 1
    #计算错误率
    errorRate = (float(errorCount) / numTestVec)
    print('the error rate of this test is : %f' % errorRate)
    return errorRate

#调用colicTest10次，求平均值
def multiTest():
    numTests = 10
    errorSum = 0.0
    for k in range(numTests):
        errorSum += colicTest()
    print('after %d iterations the average error rete is : %f ' % (numTests,errorSum / float(numTests)))

测试结果：

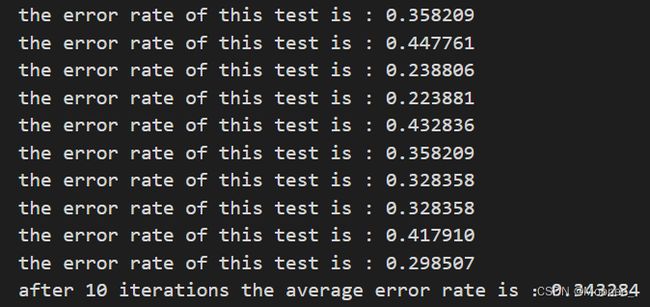
平均值为34%。因为数据集本身有30%的数据缺失。后续可以使用梯度上升法进一步改进。

总结：

• 梯度上升算法：每次更新回归系数所有样本都参与。
  优点：分类准确，获取全局最优解
  缺点：当样本比较多时，训练速度特别慢
  适用场合：样本较少的数据集
• 随机梯度下降法：每次更新回归系数只有一个样本参与。
  优点：训练速度很快
  缺点：准确率会降低，并不是朝着整体最优方向进行，容易获取到局部最优解
  适用场合：样本非常多的数据集