构建Canvas矢量图形渲染器（六）—— 二三维一体化，矢量图形自动切换三维显示。

本次给大家带来的是基于上几次canvas矢量图形渲染器的基础上做的三维方面的展示。 本系列目录

    先上demo，点击二三维切换，可以在2d 和3d 之间切换。“添加三维矩形”可以添加随机位置的不规则矩形。

 

添加3D矩形 添加3D五角星 添加2D点 添加2D圆 添加2D线
切换二维 切换三维

1.我们的等角世界。

    等角投影是一种用简单的二维图像，模拟三维图像的技术。比较真正的三维技术来说，等角投影构建的三维图像计算更简单。但始终是模拟的技术，其真实效果还有很大的差距，但是等角投影在现在的游戏界用的还是很多的。比如RPG、SLG....

    1。投影

    我们将三维物体绘制到二维平面上的过程，叫做投影。比如说用我们的眼睛观察世界其实也是一种投影的过程。

    下面我们就说说什么是等角投影：

    等角投影其实是一种轴测投影，也就是说物体的大小不会随着与相机的距离发生改变。（其实也就是说不会发生近大远小的改变）。

    下图是用我们的lib库构建的一张图片。

    

 

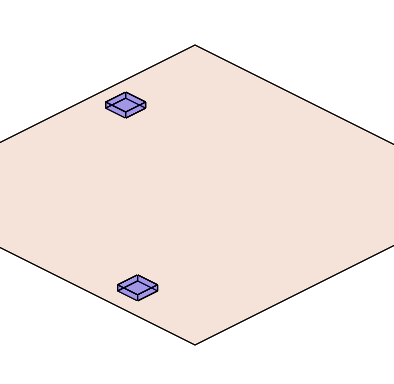
    两个矩形的长、宽、高都相等，距相机的位置不一样（按常理我们看到的图形必定是近大远小）。通过等角投影后显示在二维平面上的图形却保持了相同的大小，这就是等角投影的作用。

    在这样的投影中。X、Y、Z的夹角都回相同，如下图

    

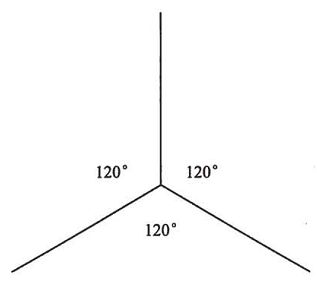
     更多的等角投影的理论知识我们可以参阅 ：Flash ActionScript 3.0 动画高级教程 这本书的第四章。

    2.等角世界与屏幕坐标的转换。

    由于我们的矢量图形是构建在世界坐标系之上的，我们在进行转换的时候需要首先将等角世界中的三维图形转换为二维世界坐标的图形，再通过以前解析二维世界坐标的方法转换为屏幕坐标。

    1.等角坐标转换为世界坐标。

    在这之前我们首先构造了一个名为Point3D的类型，来描述三维坐标下的点：

//CLASS: POINT3D类型。
function Point3D(x, y, z){
    this.x = x;
    this.y = y;
    this.z = z;
}

//转换为世界坐标，用于最后的显示
Point3D.prototype.toDisPlayPoint = function() {
    var x = this.x - this.z;
    var y = this.y * this.CORRECT + (this.x + this.z) * 0.5;
    return new Point(x, y);
}

Point3D.prototype.CORRECT =  1.2247;

Point3D.prototype.geoType = "Point3D";

Point3D.prototype.clone = function() {
    return new Point3D(this.x, this.y, this.z);
}

    这个类里面，有一个 “toDisPlayPoint” 的方法，他将三维坐标下的点转换为二维世界坐标下的点。至于那个公式是怎么来的，大家可以参考等角投影的相应知识，这里就不做详细的推导了。

    有了三维下点，我们下面需要在渲染器中对其进行解析。

//获得一个点的屏幕显示位置。
Canvas.prototype.getLocalXY = function(point, threeD) {
    threeD = threeD || this.layer.threeD;
    if(threeD && this.layer.threeD) {
        if(point.geoType !== "Point3D") {
            point = new Point3D(point.x, threeD.height, point.y);
        }
        point = point.toDisPlayPoint();
    }
    var resolution = this.layer.getRes();
    var extent = this.layer.bounds;
    var x = (point.x / resolution + (-extent.left / resolution));
    var y = ((extent.top / resolution) - point.y / resolution);
    return {x: x, y: y};
}

     首先我们判断当前的Layer是否启用了三维显示。如果启用了三维显示，那我们按照下面的方法进行操作：

     1.判断传入的点是否已经是三维点，如果不是则把二维点转换为三维点，通常三维点的y值也就是layer图层定义的y值。

     2.将三维点转换为二维世界中的点。

     3.显示二维世界中的点。

     这样我们就把三维下的点显示到屏幕上，而且实现了二维自动转三维的功能。

     ThreeD这个类现在还很简单，只有一个表示y坐标的height属性：

//CLASS:等角世界3D效果。
function ThreeD(height) {
    this.height = height;
}

    3.屏幕坐标与等角世界坐标的转换。

    1.首先我们需要把屏幕坐标转换为可显示的二维坐标

    这个我们已经在以前的随笔中实现了：

//通过屏幕坐标获取世界坐标。
Layer.prototype.getPositionFromPx = function (px) {
    return new Point((px.x + this.bounds.left / this.res) * this.res,
        (this.bounds.top/this.res - px.y) * this.res);
}

   下面我们在point类中添加下面这个两个方法，用于把二维世界坐标转换为等角世界中的坐标：

//做所显示用的point，转换为3d下的point值。
Point.prototype.disToWorldPoint3D = function(height) {
    var x = this.y + this.x * 0.5;
    var y = height || 0;
    var z = this.y - this.x * 0.5;
    return new Point3D(x, y, z);
}

//做所显示用的point，转换为世界坐标系下的point(x,0,z)值。
Point.prototype.disToWorldPoint = function(height) {
    var x = this.y + this.x * 0.5;
    var z = this.y - this.x * 0.5;
    return new Point(x, z);
}

    通过以上的步骤就把屏幕坐标转换为等角世界中的坐标啦。

 

2.二维图像中的三维属性。

    这一部分我们来说说二维图形是怎么自动变成三维的。首先我们需要区分下可以变成三维图形的类和不能变化的。

    可以三维化的类：

    所有继承自LinerRing的类（LinerRing，Star）。

    不能三维化的类：

    Circle, Point, Img。

    这三个类不能转换为三维，是因为在等角中二维的圆和三维的圆显示结构都一样，图片就不说了他本身就一二维的。

    明确了实现后我们需要为所有继承自LinerRing的图形定义一高度属性：

function Geometry(threeD){
    this.id = CanvasSketch.getId("geomtry_");
    //增加3d的属性。
    if(threeD) {
        this.threeD = threeD;
    }
}

 

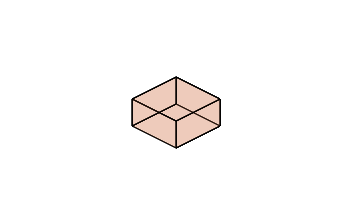
    使用的时候就非常简单了，比如说我们需要构造一个在屏幕中心的正方形，可以通过以下语句实现：

 var vectors = [];
 var points = [];
 var threeD = new ThreeD(10);
 points.push(new Point(-10, -10), new Point(-10, 10), new Point(10, 10), new Point(10, -10));
 var linerRing = new Vector(new LinerRing(points, threeD), groundStyle);
 vectors.push(linerRing);
        
 layer.addVectors(vectors);

    我们定义了一个LinerRing的三维对象，只需要和以前一样定义底面的矩形，并设置一高度程序内部就可以将其渲染为三维的矩形，如图：

    但是，不知道大家想到没有在程序内部是如何实现的？

    请看下面的代码：

Canvas.prototype.drawLinerRing = function(geometry, style, id) {        
    this.rendererPath(geometry, {fill: style.fill, stroke: style.stroke}, id);
    
    //如果我们使用的是3d世界中的绘图，且我们的图形高度大于0。
    if(this.layer.threeD && geometry.threeD && geometry.threeD.height > 0) {
        //绘制顶面。
        var linerRing3d = this.convertPathTothreeD(geometry);
        this.rendererPath(linerRing3d, {fill: style.fill, stroke: style.stroke}, id);
        //绘制侧面。
        var points2d = geometry.points;
        var points3d = linerRing3d.points;
        for(var i = 0, len = points2d.length - 1; i< len; i++) {
            var p1 = new Point3D(points2d[i].x, 0, points2d[i].y);
            var p2 = points3d[i];
            var p3 = points3d[i + 1];
            var p4 = new Point3D(points2d[i + 1].x, 0, points2d[i + 1].y);
            var edgePoints = [p1, p2, p3, p4];
            var edge = new LinerRing(edgePoints);
            this.rendererPath(edge, {fill: style.fill, stroke: style.stroke}, id);
        }
    }
    
    this.setCanvasStyle("reset");
}

Canvas.prototype.convertPathTothreeD = function(geometry) {
    var points = geometry.points;
    var height = geometry.threeD.height;
    var points3d = [];
    for(var i = 0, len = points.length; i < len; i++) {
        //每一个点加入高度。
        var point3d = new Point3D(points[i].x, height, points[i].y);
        points3d.push(point3d);
    }
    var linerRing3d = new LinerRing(points3d);
    return linerRing3d;
}

    不管是二维或是三维的图形，我们首先必须绘制底面，之后我们通过convertPathTothreeD，这个方法生成顶面并绘制，之后生成每个侧面并绘制。

    这里顶面的绘制和侧面的绘制都是传入的三维点，而底面是二维点。

 

3.二三维切换

    这个就很easy了，我们已经实现了二维和三维的显示只需要这样调用就可以了：

//切换2D显示。
function changetwoD() {
    layer.threeD = null;
    layer.reDraw();
}

//切换3D显示。
function changethreeD() {
    layer.threeD = threeD;
    layer.reDraw();
}

    redraw方法其实就是重绘了一遍当前中心点，当前zoom的渲染器。

Layer.prototype.reDraw = function() {
    this.moveTo(this.zoom, this.center);
}

    至此我们就将一个基本的二三维一体化的渲染器做好了，当然我们这里还有很多缺陷：不能前后排序，没有光照等等。。在以后的随笔中会慢慢加入这些

    下次预告： 1.三维景深排序。

                   2.多图层叠加显示。

    尝试一下：下载本次随笔所有源码+DEMO，大家可以自己玩玩，里面还有不上东西在本次随笔中没有讲到，如范围的三维转换等。。

   点击下载。