PyTorch入门教程1.2 - Autograd: 自动微分

Autograd: 自动微分

PyTorch中所有神经网络的中心是autograd包。我们首先简单地看下这个包，然后来训练我们的第一个神经网络。

autograd包可以对所有在Tensors上进行的操作进行自动微分(differentiation)。它是一个由运行定义(define-by-run)的框架，意味着你的反向传递是由你的代码运行过程来定义的，并且每个单步的迭代都可以被微分。

让我们用更简单的术语和一些例子来看看。

Tensor

torch.Tensor是这个包的中心类。如果你将它的属性.requires_grad设置为True，它就会开始去跟踪所有对它的操作。当你完成你的计算，你可以调用.backward()，然后梯度就会自动被计算。这个tensor的梯度将被累积进.grad属性。

要停止一个tensor的历史跟踪，你可以调用.detach()，来将这个tensor从计算历史中分离出来，并且阻止之后的计算被跟踪。

为了阻止历史跟踪(以及内存的使用)，你也可以将代码块封装进with torch.no_grad():。在评估一个模型时，这种操作会特别有用，因为这个模型可能有requires_grad=True的可训练参数，但是在评估时我们不需要计算梯度。

还有一个类对自动梯度实现非常重要——Function。

Tensor 和 Function互相连接，构建起一个非循环图，它编码了完整的计算历史。每个tensor会有一个.grad_fn属性，它指代创建该Tensor的Function(用户创建的Tensors除外，它们grad_fn是None)。

如果你想计算偏导，可以在一个Tensor上调用.backward()。如果Tensor是一个标量(也就是说它只保存了一个元素数据)，则没必要声明.backward()的任何参数；当如果它有多个元素，则需要声明一个gradient参数，一个有着相匹配shape的tensor。

import torch

创建一个tensor，设置requires_grad=True，来跟踪计算：

x = torch.ones(2, 2, requires_grad=True)
print(x)

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)

进行一个tensor操作：

y = x + 2
print(y)

tensor([[3., 3.],
        [3., 3.]], grad_fn=)

y是由操作的结果创建的，所有它有grad_fn：

print(y.grad_fn)

在y进行更多操作：

z = y * y * 3
out = z.mean()

print(z, out)

tensor([[27., 27.],
        [27., 27.]], grad_fn=) tensor(27., grad_fn=)

.requires_grad_(...)in-place改变一个已有Tensor的requires_grad标志，默认为False：

a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
b = (a * a).sum()
print(a.requires_grad)
print(b.grad_fn)

False
None

a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)

True

Gradients

现在来看反向传递。

因为 out只包含一个标量，out.backward()等价于 out.backward(torch.tensor(1.))。

out.backward()

输出导数 d(out)/dx

print(x.grad)

tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])

应该是会得到一个元素全为4.5的矩阵。简称Tensor out为“$o$”。有$o=\frac{1}{4}{\sum }_i{z}_i=\frac{1}{4}{\sum }_{i}3(x_i+2{)}^2$。因此，$\frac{\partial o}{\partial x_i}{|}_{x_i=1}=\frac{\partial o}{\partial z_i}\ast \frac{\partial z_i}{\partial x_i}=\frac{1}{4}\ast 6(x_i+2)=\frac{9}{2}=4.5$。

数学上，如果有一个向量值函数$y=f(x)$，则$y$对$x$的梯度就是一个Jacobian矩阵：

一般来说，torch.autograd是一个计算vector-Jacobian乘积的引擎。就是说，给定任意向量$v={\left(\begin{array}{cccc}{v}_1& v_2& \cdots & v_m\end{array}\right)}^T$，计算乘积$v^T\cdot J$。如果$v$是一个标量函数$l=g\left(y\right)$的梯度，即$v={\left(\begin{array}{ccc}\frac{\partial l}{\partial y_1}& \cdots & \frac{\partial l}{\partial y_m}\end{array}\right)}^T$，按照链式法则，vector-Jacobian乘积就是$l$对$x$的导数：

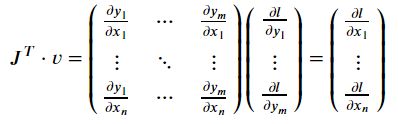
(注意，$v^T\cdot J$给出的是行向量，但也可以通过$J^T\cdot v$来当作列向量处理。)

vector-Jacobian乘积的特性使得将外部梯度输入具有非标量输出的模型非常方便。

现在我们来看一个vector-Jacobian乘积的例子：

x = torch.randn(3, requires_grad=True)
print(x)

y = x * 2
while y.data.norm() < 1000: #也可以直接写y.norm(), norm()计算y的p-范数，默认p=2
    y = y * 2

print(y)

tensor([-0.7660, -0.9496, -0.2411], requires_grad=True)
tensor([-784.4009, -972.4387, -246.9176], grad_fn=)

这个例子中y不再是一个标量，torch.autograd不能直接计算全部的Jacobian，但是如果我们只是想要vector-Jacobian乘积，只需要简单地传入一个向量作为backward 的参数:

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)

print(x.grad)

tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])

再来一个例子：

x = torch.tensor([[1,2,4],[3,1,2]], dtype=torch.float, requires_grad=True)
print(x)

y = x + 2
z = y * y
print(z)

z.backward(torch.ones_like(x))
print(x.grad) #计算得到的就是z相对于x的导数

tensor([[1., 2., 4.],
        [3., 1., 2.]], requires_grad=True)
tensor([[ 9., 16., 36.],
        [25.,  9., 16.]], grad_fn=)
tensor([[ 6.,  8., 12.],
        [10.,  6.,  8.]])

也可以通过将代码块封装进with torch.no_grad()，来暂停.requires_grad=True的Tensors的历史跟踪。

print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
	print((x ** 2).requires_grad)

print((x ** 2).requires_grad)

True
True
False
True

延展阅读

autograd 和 Function 的文档在https://pytorch.org/docs/autograd