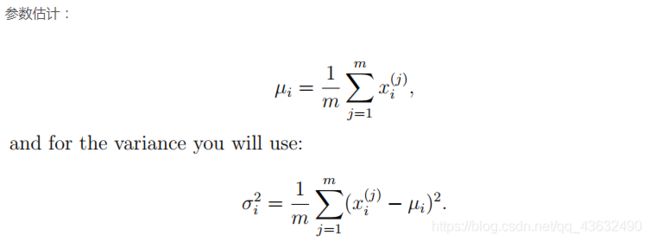15、异常检测

"""
这部分，您将实现一个异常检测算法来检测服务器计算机中的异常行为。
他的特征是测量每个服务器的响应速度(mb/s)和延迟(ms)。
当你的服务器运行时，你收集到了m=307的样本，是无标签的。
你相信其中绝大多数样本是正常的，但还是有一小部分的样本是异常的。

我们将使用高斯分布模型来检测数据集中的异常样本。
"""
import pandas as pd
import numpy as np
from scipy.io import loadmat
import matplotlib.pyplot as plt

# 加载数据
mat = loadmat('data/ex8data1.mat')
print(mat.keys())  # dict_keys(['__header__', '__version__', '__globals__', 'X', 'Xval', 'yval'])
X = mat['X']  # 训练集，无标签
Xval, yval = mat['Xval'], mat['yval']  # 验证集，有标签
print(X.shape, Xval.shape, yval.shape)  # (307, 2) (307, 2) (307, 1)


def plot_data():
    # 可视化数据集
    plt.figure(figsize=(8, 5))
    plt.plot(X[:, 0], X[:, 1], 'bx')  # 散点图，蓝色小叉


plot_data()
plt.show()

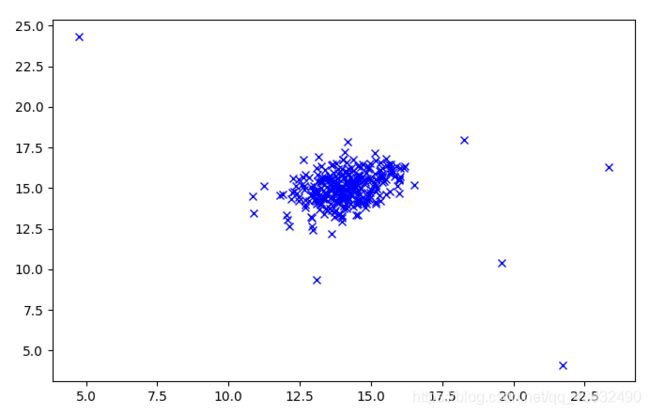
多变量高斯分布：

def gaussian(X, mu, sigma2):
    '''
    计算高斯分布概率
    Args:
        X: 训练集
        mu:平均值矩阵
        sigma2:方差

    Returns:
        一个(m, )向量，包含每个样本的概率值
    '''
    m, n = X.shape
    if np.ndim(sigma2) == 1:  # np.ndim()计算数组的维度
        sigma2 = np.diag(sigma2)  # 转换为对角矩阵形式
    norm = 1. / (np.power((2 * np.pi), n / 2) * np.sqrt(np.linalg.det(sigma2)))  # 公式第一项
    # np.sqrt()取平方根 ， np.linalg.det()矩阵求行列式
    exp = np.zeros((m, 1))  # 公式第二项
    for row in range(m):
        xrow = X[row]  # 遍历每一个训练样本
        exp[row] = np.exp(
            -0.5 * ((xrow - mu).T).dot(np.linalg.inv(sigma2)).dot(xrow - mu))  # dot()矩阵乘法 , np.linalg.inv()矩阵求逆
    return norm * exp  # 返回高斯概率，一个(m, )向量

# 参数估计
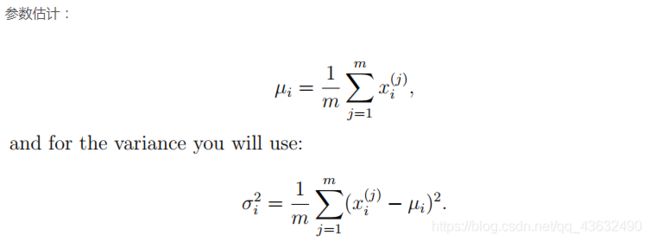
def getGaussianParams(X, useMultivariate):
    '''
    计算均值与方差
    Args:
        X: 训练集
        useMultivariate:是否使用多元高斯分布

    Returns:
        均值(mu)，方差(sigma2)
    '''
    mu = X.mean(axis=0)  # 按列求均值
    if useMultivariate:
        sigma2 = ((X - mu).T @ (X - mu)) / len(X)  # 多元高斯：计算协方差矩阵
    else:
        sigma2 = X.var(axis=0, ddof=0)  # 一元高斯：计算方差数值（除以m）
    return mu, sigma2

# 画高斯分布图形
def plotContours(mu, sigma2):
    '''
    画出高斯概率分布的图，在三维中是一个上凸的曲面。投影到平面上则是一圈圈的等高线。
    Args:
        mu:平均值
        sigma2:方差
    '''
    delta = .3  # delta不能太小,否则会生成太多的数据，导致矩阵相乘会出现内存错误。
    x = np.arange(0, 30, delta)
    y = np.arange(0, 30, delta)
    xx, yy = np.meshgrid(x, y)  # 生成网格点坐标矩阵
    points = np.c_[xx.ravel(), yy.ravel()]  # 按列合并坐标，第一列为横坐标，第二列为纵坐标。
    z = gaussian(points, mu, sigma2)  # 计算高斯分布概率
    z = z.reshape(xx.shape)  # 重塑结果为网格坐标
    cont_levels = [10 ** h for h in range(-20, 0, 3)]  # 等高线的条数，这个levels是作业里面给的参考,或者通过求解的概率推出来。
    '''
    cont_levels ： [1e-20, 1e-17, 1e-14, 1e-11, 1e-08, 1e-05, 0.01]
    '''
    plt.contour(xx, yy, z, cont_levels)  # 绘制等高线
    plt.title('Gaussian Contours', fontsize=16)


# 不使用多元高斯的情况
plot_data()
useMV = False
plotContours(*getGaussianParams(X, useMV))  # *表示解元祖
# 使用多元高斯的情况
plot_data()
useMV = True
plotContours(*getGaussianParams(X, useMV))
plt.show()
'''
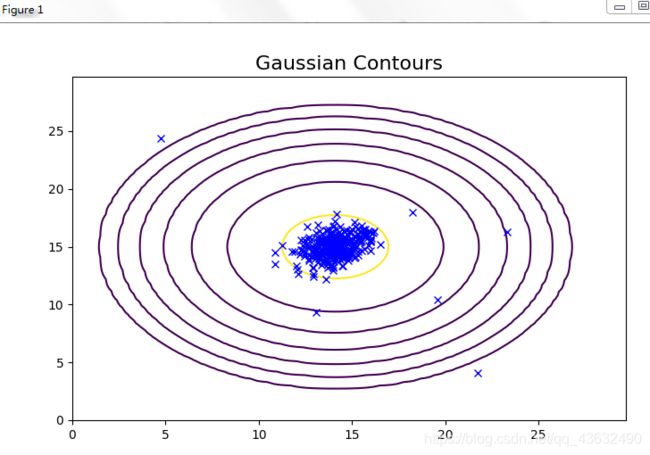
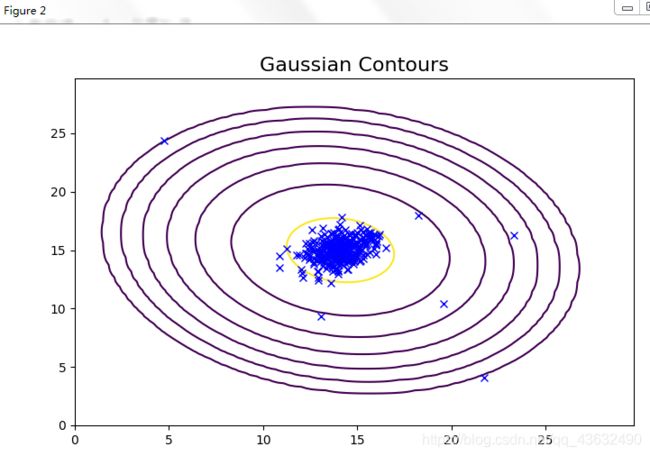
从上面的图可以看到，一元高斯模型仅在横向和纵向上有变化，
而多元高斯模型在斜轴上也有相关变化，对应着特征间的相关关系。
而一元高斯模型就是多元高斯模型中协方差矩阵为对角矩阵的结果，即协方差都为0，不考虑协方差，只考虑方差，故一元高斯模型不会有斜轴上的变化。

从上面的图我们可以清晰的看到，哪些样本的概率高，哪些样本的概率低，概率低的样本很大程度上就是异常值。
'''

# 根据验证集选择合理阈值，小于这个阈值就设定为异常
def selectThreshold(yval, pval):
    '''
    选择最佳的阈值
    Args:
        yval:验证集样本结果
        pval:模型预测结果

    Returns:
        最佳的F1值：bestF1，最佳的阈值：bestEpsilon
    '''

    def computeF1(yval, pval):
        '''
        计算F1值
        Args:
            yval:验证集样本结果
            pval:模型预测结果

        Returns:
            F1值
        '''
        m = len(yval)
        tp = float(len([i for i in range(m) if pval[i] and yval[i]]))  # ture positive 有多少的样本判断为真异常值 （异常：1，正常：0）
        fp = float(len([i for i in range(m) if pval[i] and not yval[i]]))  # false positive 有多少样本判断为假的异常值
        fn = float(len([i for i in range(m) if not pval[i] and yval[i]]))  # false negative 有多少样本判断为假的正常值
        prec = tp / (tp + fp) if (tp + fp) else 0  # 准确率
        rec = tp / (tp + fn) if (tp + fn) else 0  # 召回率
        F1 = 2 * prec * rec / (prec + rec) if (prec + rec) else 0  # F1值
        return F1

    epsilons = np.linspace(min(pval), max(pval), 1000)  # 阈值的候选值
    bestF1, bestEpsilon = 0, 0  # 存储最佳的F1值，最佳的阈值
    # 挑选最佳阈值
    for e in epsilons:
        pval_ = pval < e  # True则异常，False为正常,pval_是一个布尔型的一维数组
        thisF1 = computeF1(yval, pval_)  # 当前阈值下的高斯异常检测模型的F1值
        # 遇见更佳的值就更新结果
        if thisF1 > bestF1:
            bestF1 = thisF1
            bestEpsilon = e
    return bestF1, bestEpsilon


mu, sigma2 = getGaussianParams(X, useMultivariate=True)  # 计算多元高斯分布的参数（训练集）
pval = gaussian(Xval, mu, sigma2)  # 高斯异常检测模型的预测结果（验证集）
bestF1, bestEpsilon = selectThreshold(yval, pval)  # 计算最佳F1和阈值
print(bestF1, bestEpsilon)  # 0.8750000000000001 [9.07484457e-05]

# 运用得出的阈值判断训练集中哪些是异常样本
y = gaussian(X, mu, sigma2)  # 计算训练集的高斯概率
xx = np.array([X[i] for i in range(len(y)) if y[i] < bestEpsilon])  # xx存储预测出的异常样本组成的数组
print(xx.shape)  # (6, 2) 共预测出了6个异常样本

# 可视化异常样本
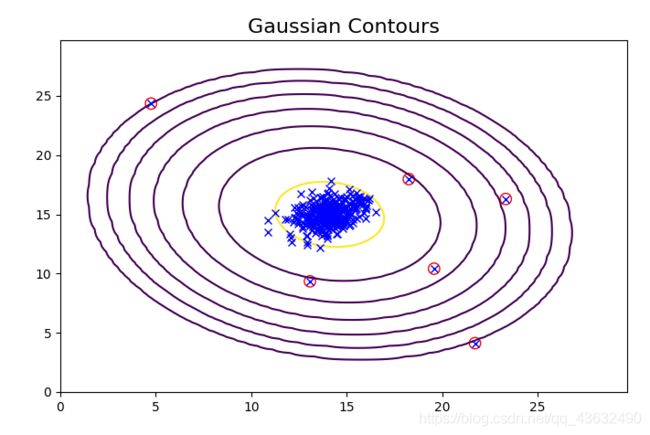
plot_data()  # 源数据
plotContours(mu, sigma2)  # 绘制高斯等高线
plt.scatter(xx[:, 0], xx[:, 1], s=80, facecolors='none', edgecolors='r')  # 用红色空心散点标记出异常样本
plt.show()

# 高维度数据集下的异常检测算法
mat = loadmat('data/ex8data2.mat')
print(mat.keys())  # dict_keys(['__header__', '__version__', '__globals__', 'X', 'Xval', 'yval'])
X2 = mat['X']  # 训练集
Xval2, yval2 = mat['Xval'], mat['yval']  # 验证集
print(X2.shape, Xval2.shape, yval2.shape)  # (1000, 11) (100, 11) (100, 1)
mu, sigma2 = getGaussianParams(X2, useMultivariate=True)  # 高斯参数
ypred = gaussian(X2, mu, sigma2)  # 高斯概率值（训练集）
# 阈值选择
yval2pred = gaussian(Xval2, mu, sigma2)  # 高斯概率值（验证集）
bestF1, bestEpsilon = selectThreshold(yval2, yval2pred)  # 根据验证集计算出的最佳F1值和最佳阈值
anoms = np.array([X2[i] for i in range(len(ypred)) if ypred[i] < bestEpsilon])  # 训练集的异常样本数组
print(bestEpsilon, anoms.shape)  # [1.75560448e-18] (122, 11)
# 不使用多元高斯分布的结果：[1.3786075e-18] (117, 11)