模型优化-梯度下降算法

梯度下降（Gradient Descent）算法是机器学习中使用非常广泛的优化算法。当前流行的机器学习库或者深度学习库都会包括梯度下降算法的不同变种实现。

【思想】：要找到某函数的最小值，最好的方法是沿着该函数的梯度方向探寻，例如物理学上的加速度与速度的关系。当加速度为零时，此时速度可能是最大，也有可能是最小，这取决于函数曲线。

【步骤】：

1. 随机取一个自变量的值 $x_0$；
2. 对应该自变量算出对应点的因变量值：$f(x_0)$；
3. 计算 $f(x_0)$ 处目标函数 f(x) 的导数；
4. 从 $f(x_0)$ 开始，沿着该处目标函数导数的方向，按一个指定的步长 α，向前“走一步”，走到的位置对应自变量取值为 $x_1$。换言之，$|x_0-x_1|/\alpha =f(x)$ 在 $f(x_0)$ 处的斜率；
5. 继续重复步骤 2 - 4，直至满足结束条件，退出迭代。

梯度下降法作为机器学习中较常使用的优化算法，有三种不同的形式：批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）以及小批量梯度下降（Mini-Batch Gradient Descent）。其中小批量梯度下降法也常用在深度学习中，对模型进行训练。

为了便于理解，我们以只有一个特征的线性回归模型作为案例，准备工作如下：

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt


# y = 5x + 2
dataset = np.array([
    [1, 7],
    [2, 13],
    [3, 17],
    [4, 22],
    [5, 27],
    [6, 33],
    [7, 38],
    [8, 42],
    [9, 46],
    [10, 52]
])
x = dataset[:, 0]
y = dataset[:, 1]

该线性回归的函数可设置为：
$$f(x_i;\theta )=w_1{x}_i+b$$
其中，w 为系数向量，b 为偏置，i = 1, 2, …, m 表示样本数，θ 表示所有要求的参数（w 和 b）。对应的目标函数即：
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(f(x_i;w)-y_i{)}^2$$

通常我们会把 b 添加到 w 中，构成一个新的系数向量 w’，同时也相应扩充 x 使其变为 x’。
$$\begin{gathered} w^{\prime T}=[w,b]x^{\prime }=[x,1] \\ f(x_1^{\prime };w^{\prime })=w^{\prime }{x}^{\prime } \end{gathered}$$
对于上述示例，只有一个特征，所以 $w^{\prime T}=[w_1,b]$。此外，需要注意的是，$x_i$ 表示第 i 个样本，$x^i$ 表示样本第 i 个特征。

在开始具体讲述梯度下降算法之前，先介绍向量化概念。

向量化

向量化是去除代码中 for 循环的艺术，尤其当数据集非常大时，运行向量化是一个可以节省大量运行时间的关键技巧。我们仍然用上面所讲的例子来说明什么是向量化。

在线性回归中，我们需要获得模型的输出值，即计算 $f(x)=w^{T}x+b$，其中 w 和 x 都是列向量。假设此刻有一个拥有非常多特征的数据集，你想用非向量化方法去计算 f(x)，则代码如下：

f = 0
for i in range(dataset_length):
    f += w[i] * x[i]
f += b

非向量化需要从数据集中获取每一条数据，并按照 f(x) 的计算公式逐一计算，然后将其累加。而向量化则通过矩阵乘法并行化处理，在此我们使用 numpy 的 dot() 函数。

f = np.dot(w, x) + b

为了证明向量化的计算开销比非向量化要小很多，可以运用下面的小例子来查看两种方式的计算时间。

import numpy as np # 导入numpy库
a = np.array([1,2,3,4]) # 创建一个数据a
print(a)
# [1 2 3 4]

import time # 导入时间库
a = np.random.rand(1000000)
b = np.random.rand(1000000) # 通过round随机得到两个一百万维度的数组
tic = time.time() # 现在测量一下当前时间

# 向量化的版本
c = np.dot(a,b)
toc = time.time()
print("Vectorized version:" + str(1000*(toc-tic)) +"ms") # 打印一下向量化的版本的时间

# 继续增加非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):
    c += a[i]*b[i]
toc = time.time()
print(c)
print("For loop:" + str(1000*(toc-tic)) + "ms") # 打印for循环的版本的时间

最后的输出结果为：

[1 2 3 4]
Vectorized version:70.01662254333496ms
249924.36248504242
For loop:1096.3506698608398ms

不同电脑的性能有所差异，最终获得的结果也不尽相同，但唯一不变的是向量化的计算时间要远小于非向量化的计算时间。因此，在后续的代码部分我们都将使用向量化的方式进行梯度计算。关于向量化的更多内容，可以去观看吴恩达老师的深度学习课程第一堂课第一周 传送门

批量梯度下降

批量梯度下降法是最原始的形式，在每一次迭代时使用所有样本来进行梯度的更新。

【步骤】：

1. 对目标函数求偏导。
   $$\frac{\partial J(w^{\prime })}{\partial w^{\prime }}=\frac{1}{m}\sum _{i=1}^m(f(x_i^{\prime };\theta )-y_i)x^{\prime j}$$
   其中，i = 1, 2, …, m 表示样本数，j = 0, 1 表示特征数。
2. 每次迭代对参数进行更新：
   $$w_j:=w_j-\alpha \frac{\partial J(w^{\prime })}{\partial w^{\prime }}=\frac{1}{m}\sum _{i=1}^m(f(x_i^{\prime };\theta )-y_i)x^{\prime j}$$

【代码实现】：

def BatchGradientDescent(x, y, step=0.001, iter_count=500):
    length, features = x.shape
    
    # 整合系数向量 w' 和新样本集 x'
    data = np.column_stack((x, np.ones((length, 1))))
    w = np.zeros((features + 1, 1))
    
    # 开始迭代
    for i in range(iter_count):
        new_w = w.copy()
        for feature in range(features + 1):
            new_w[feature] = np.sum((np.dot(data, w) - y) * data[:, feature]) / length
        w -= step * new_w        
    return w

print(BatchGradientDescent(x, y, iter_count=500))
# 输出：
array([[5.2272],
       [0.9504]])

【优点】：

• 一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行。
• 由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。

【缺点】：

• 当数据集 m 很大时，每迭代一步都需要对所有样本进行计算，训练过程会很慢。
• 内存容量可能支撑不了如此巨大的数据集。

随机梯度下降

随机梯度下降法不同于批量梯度下降，每次迭代使用一个样本来对参数进行更新，使得训练速度加快。

【代码实现】：

def StochasticGradientDescent(x, y, step=0.001, iter_count=500):
    length, features = x.shape
    
    # 整合系数向量 w' 和新样本集 x'
    data = np.column_stack((x, np.ones((length, 1))))
    w = np.zeros((features + 1, 1))

    # 开始迭代
    for i in range(iter_count):
        # 随机选择一个样本
        random_ind = np.random.randint(length)
        new_w = w.copy()
        for feature in range(features + 1):                        
            new_w[feature] = (np.dot(data[random_ind:random_ind + 1], w) - y[random_ind]) * data[random_ind, feature] / length
        w -= step * new_w        
    return w
    

print(StochasticGradientDescent(x, y, iter_count=1000))
# 输出：
array([[5.09770338],
       [0.77370206]])

除了随机选择数据集中的样本之外，我们也可以按照数据集中的样本顺序，依次选择样本。不过样本的特定顺序可能会给算法收敛带来一定的影响，因此推荐随机选取样本。

def StochasticGradientDescent(x, y, step=0.001, iter_count=500):
    length, features = x.shape
    
    # 整合系数向量 w' 和新样本集 x'
    data = np.column_stack((x, np.ones((length, 1))))
    w = np.zeros((features + 1, 1))
    random_ind = 0
    
    # 开始迭代
    for i in range(iter_count):
        random_ind = (random_ind + 1) % length
        new_w = w.copy()
        for feature in range(features + 1):                        
            new_w[feature] = (np.dot(data[random_ind:random_ind + 1], w) - y[random_ind]) * data[random_ind, feature] / length
        w -= step * new_w        
    return w

【优点】：由于不是全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。

假设我们现在有 30w 个样本，对于批量梯度下降而言，每次迭代需要计算 30w 个样本才能对参数进行一次更新。而对于随机梯度下降而言，参数每次更新只需要一个样本。因此，若使用这 30w 个样本进行参数更新，则参数会被更新 30w 次。在这期间，随机梯度下降就能保证收敛到一个合适的最小值上。

【缺点】：

• 准确度下降：随机梯度下降仅考虑单个样本的损失函数，容易受噪声数据的影响，因此准确度无法与批量梯度下降相比。
• 可能会收敛到局部最优：由于单个样本不能代表全体样本的趋势，尤其随机选取的样本恰好是噪声，则很有可能偏离最优值。
• 不易于并行实现：因为每次迭代过程中只计算一个样本的损失函数，没能利用向量化所带来的计算优势。

山谷震荡与鞍部停滞

不论是机器学习还是深度学习的优化问题，存在众多局部极小值陷阱。这些陷阱对于批量梯度下降、小批量梯度下降以及随机梯度下降都是普遍存在的。但对于随机梯度下降而言，可怕的不是落在局部极小值陷阱，而是山谷和鞍部这两类地形。

【山谷震荡】：山谷顾名思义就是狭长的山间小道，左右两边是峭壁，见下图。

在梯度下降算法中，下降最快的方向始终是垂直等高线并指向谷底的方向。在山谷这一类地形中，很容易从山谷的一端撞向山谷的另一端，并且随机梯度下降粗糙的梯度估计使得它在两山壁之间来回反弹震荡的概率增加，不能沿山道方向迅速下降，导致收敛不稳定和收敛速度慢。

特征归一化方法可以有效地减少山谷地形，从而削减山谷震荡现象发生的可能。

【鞍部停滞】：鞍部的形状像一个马鞍，一端上升，另一端下降，而中心区域是一片近乎水平的平地，可以想象成在一座峰峦叠错连绵不绝的山脉中突然出现了一片平原。

随机梯度下降来到鞍部，由于坡度不明显，且单个样本的梯度方向不一定指向谷底，因此非常容易陷在鞍部，缓慢而无方向地乱走。若鞍部范围较广，随机梯度下降很有可能就困在此处，无法走出鞍部范围。

【解决方案】：保持下降的惯性、加大对环境的感知，具体做法请参考模型优化的其他方法。

小批量梯度下降

小批量梯度下降是对批量梯度下降以及随机梯度下降的一个折中方案，其思想是每次迭代使用 batch_size 数量的样本来对参数进行更新。

【代码实现】：

def MiniBatchGradientDescent(x, y, step=0.001, iter_count=500, batch_size=4):
    length, features = x.shape
    
    # 整合系数向量 w' 和新样本集 x'
    data = np.column_stack((x, np.ones((length, 1))))
    # 消除样本顺序带来的影响
    np.random.shuffle(data)
    w = np.zeros((features + 1, 1))
    start, end = 0, batch_size
    
    # 开始迭代
    for i in range(iter_count):        
        new_w = w.copy()
        for feature in range(features + 1):
            new_w[feature] = np.sum((np.dot(data[start:end], w) - y[start:end]) * data[start:end, feature]) / length
        w -= step * new_w
        start = (start + batch_size) % length
        end = (end + batch_size) % length
    return w


print(MiniBatchGradientDescent(x, y))
# 输出：
array([[5.25089298],
       [1.09047361]])

有的时候，数据的特定顺序会给算法收敛带来影响，因此一般会在每次遍历训练数据之前，先对所有的数据进行随机排序。

【优点】：

• 向量化能够使得计算一个 batch 数量样本所需的时间与计算单个样本所需的时间相差无几。
• 每次使用一个 batch 可以大大减小随机梯度下降收敛所需要的迭代次数，同时可以使收敛到结果更加接近梯度下降的效果。

对比批量梯度下降和随机梯度下降，二者都不需要考虑样本的数量，批量梯度下降直接选用全部样本，而随机梯度下降则随机选取一个样本。但对于小批量梯度下降而言，batch_size 该如何设置，是一个问题。

结合小批量梯度下降算法的优点，我们来谈论下 batch_size 的选择。

【增大 batch_size】：

• 可以充分发挥向量化的作用，不仅可以提高内存利用率，同时提升计算性能。
• batch_size 越大，则遍历全部样本（epoch）所需 的迭代次数也越少，对于相同数据量的处理速度进一步加快。
• batch_size 越大，则选取的样本数也越多，越能代表整个数据集，那么根据梯度确定的下降方向也越准确。需要注意的是，当 batch_size 增大到一定程度后，下降方向基本不会再发生变化。

但需要注意的是，我们也不能盲目增大 batch_size，一旦 batch_size 过大，仍然会面临批量梯度下降的问题——内存容量可能撑不住。此外，跑完一次 epoch 所需的迭代次数减少，相应的参数更新次数也变少，对准确度也会造成一定的影响。

一般来说，batch_size 取 2 的幂次时能充分利用矩阵运算操作，所以可以在 2 的幂次中挑选最优的取值，例如 32、64、128、256 等。

三类梯度下降算法的比较

通过上述的分别介绍，批量梯度下降、随机梯度下降以及小批量梯度下降的计算公式都是相同的，唯一的区别就是在每轮迭代中参与的样本数量。

• 批量梯度下降：全部样本；
• 随机梯度下降：单个样本；
• 小批量梯度下降：一个 batch 样本。

在性能以及准确性方面，小批量梯度下降综合了批量梯度下降和随机梯度下降的优点，从而缓解了两者的缺陷。批量梯度下降计算开销大，随机梯度计算快但准确率不够高。下批量梯度下降通过设置 batch，在计算速度方面不逊色于随机梯度下降，并且迭代次数比随机梯度要少，总的来说反而比随机梯度更快收敛。此外，小批量梯度下降相比随机梯度下降准确率更高，因为它选取一个 batch 的样本，可以在一定程度上减少噪声的影响。

上图选自博客 批量梯度下降(BGD)、随机梯度下降（SGD）以及小批量梯度下降(MBGD)的理解，若构成侵权，则立即删除。

这三类算法的相关代码都可以在该传送门中获得。

讲完了这三类梯度下降算法，我们再来讨论下在梯度下降算法中出现的超参数 α、迭代终止条件以及算法所遇到的难点。

超参数 α

超参数 α 又叫做步长，用于确定找到最小值点而尝试在目标函数上前进的步伐到底走多大。如果该参数设置的大小不合适，则会导致最终无法找到最小值点。

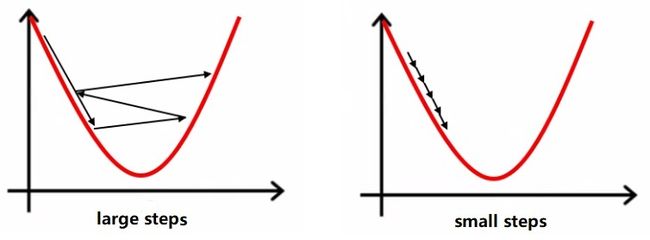
比如下面左图就是因为步幅太大，几个迭代后反而取值越来越大。修改成右图那样的小步伐就可以顺利找到最低点。

不过大步伐也不是没有优点。步伐越大，每一次前进得越多。步伐太小，虽然不容易“跨过”极值点，但需要的迭代次数也多，相应需要的运算时间也就越多。

为了平衡大小步伐的优缺点，也可以在一开始的时候先大步走，当所到达点斜率逐渐下降——函数梯度下降的趋势越来越缓和——以后，逐步调整，缩小步伐。比如下图这样：

算法难点

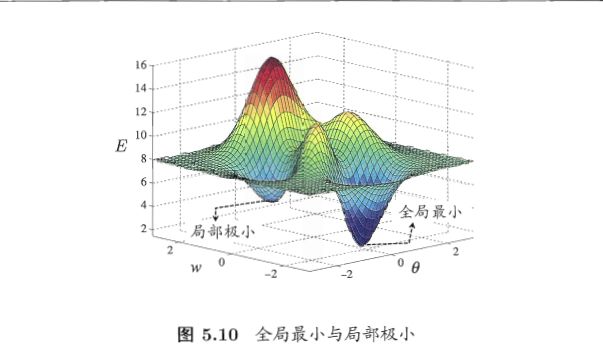
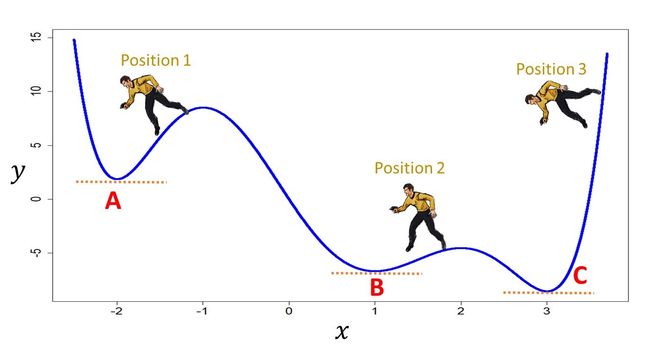
即使步伐合适，也不一定能够找到最小值点。如果目标函数有多个极小值点（多个向下的“弯儿”），那么如果开始位置不妥，很可能导致最终是走到了一个局部极小值就无法前进了。

【解决方案】：如果目标函数不能确定只有一个极小值，而获得的模型结果又不令人满意时，就该考虑是否是在学习的过程中，优化算法进入了局部而非全局最小值。这种情况下，可以尝试几个不同的起始点。甚至尝试一下大步长，说不定反而能够跨出局部最小值点所在的凸域。

迭代结束的条件

梯度下降法（梯度上升法应该也适用）迭代结束的条件，常用的有两种：

• 定义一个合理的阈值，当两次迭代之间的差值小于该阈值时，迭代结束。
• 设置一个大概的迭代步数，比如 1000 或 500，梯度下降法最终的迭代肯定会收敛，只要达到相应迭代次数，多了也没关系。因为迭代次数多了后，在到达极值点时，函数对变量的导数已近乎为 0，即使过了极值点，导数就变为正数了，之前的导数为负数。这个时候，变量 x 的值减去步长与导数的乘积反倒变小了。所以即使步数多了，结果也基本上就在极值点处左右徘徊，几乎等于极值点，因此没有问题。

参考

• 最常用的优化算法——梯度下降法：https://gitchat.csdn.net/column/5ad70dea9a722231b25ddbf8/topic/5b19c29485f83d502a1c01a4
• 线性回归——从模型函数到目标函数：https://gitchat.csdn.net/column/5ad70dea9a722231b25ddbf8/topic/5b1db764096f3a3c830eb2b8
• 线性回归——梯度下降法求解目标函数：https://gitchat.csdn.net/column/5ad70dea9a722231b25ddbf8/topic/5b20586fe6a93576476f6b19
• 梯度下降法迭代结束的条件：https://blog.csdn.net/hyg1985/article/details/42556847
• 批量梯度下降(BGD)、随机梯度下降（SGD）以及小批量梯度下降(MBGD)的理解：https://www.cnblogs.com/lliuye/p/9451903.html