计算机视觉——SIFT算法之高斯金字塔

计算机视觉—SIFT算法之高斯金字塔

[email protected]

1、高斯金字塔–>DoG金字塔

       在理论上，输入图像需要先分别与不同尺度的高斯核进行卷积，然后求两幅图像的差。而在实际中更为简单，如图所示，高斯金字塔相邻两层相减，便可以得到 DoG 金字塔。这是因为，高斯金字塔每层中的多幅图像，原本就是通过对同一幅输入图像进行不同尺度的高斯卷积得来的。关于高斯金字塔的构造方法，请继续阅读下文。

D(x,y,σ)=(G(x,y,kσ)−G(x,y,σ))∗I(x,y)

2、SIFT算法中的高斯金字塔

       图像金字塔模型是指，将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，自底向上构成的塔状模型。原始图像为金字塔的第一层，每次降采样得到的新图像为金字塔的一层（每层一张图像）。

       SIFT算法中的高斯金字塔略有不同。为了让尺度体现其连续性，在简单下采样的基础上添加了多尺度的高斯滤波。一幅图像可以产生几组（Octave）图像，一组图像又包括几层（Interval）图像，并且组数和金字塔的层数相等。





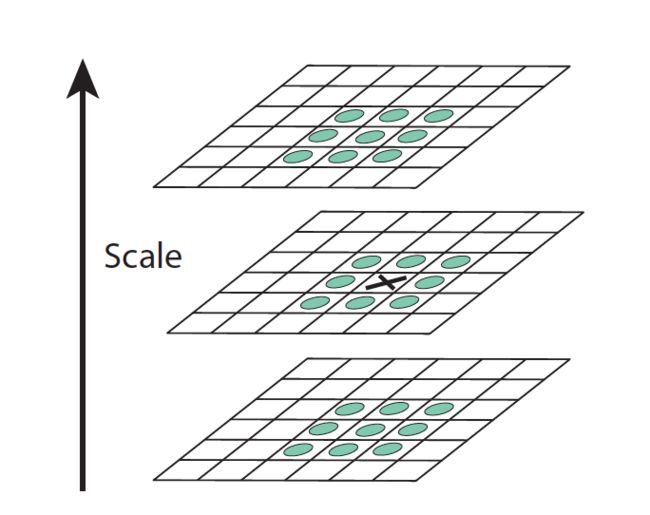
       为了在每组图像中检测 S 个尺度的极值点，DoG 金字塔每组需 S+2 层图像，因为每组的第一层和最后一层图像上不能检测极值，如图；而 DoG 金字塔由高斯金字塔相邻两层相减得到，则高斯金字塔每组需 S+3 层图像，实际计算时 S 通常在3到5之间。SIFT算法中生成高斯金字塔的规则如下：

       设高斯金字塔共包含 O 组图像，每组图像有 S+3 层，

O=log2(min{M,N})−3

其中， M,N 分别为原始图像的行数和列数。

       设位于金字塔底的第1组的第1层图像，其高斯滤波的尺度为

σ(o=1,s=1)=σ(1)1

则位于第1组的其它层图像的高斯滤波尺度分别为


       σ(o=1,s=2)=σ(1)2=kσ(1)1

       σ(o=1,s=3)=σ(1)3=kσ(1)2=k2σ(1)1

              ⋯

       σ(o=1,s=S+3)=σ(1)S+3=kσ(1)S+2=⋯=kS+2σ(1)1


同理，位于第2组的各层图像的高斯滤波尺度分别为


       σ(o=2,s=1)=σ(2)1

       σ(o=2,s=2)=kσ(2)1

       σ(o=2,s=3)=k2σ(2)1

              ⋯

       σ(o=2,s=S+3)=kS+2σ(2)1


其中， k 为相邻尺度的缩放因子

k=21S

为了保证尺度变化的连续性， 第2组第1层的尺度等于第1组倒数第3层的尺度，即

σ(2)1=kSσ(1)1=2σ(1)1

不难发现，相邻两组的同一层，其尺度为2倍关系。进一步归纳可知，位于第 o 组，第 s 层图像的图像的尺度为

σ(o,s)=σ(o)s=2o−1ks−1σ(1)1,o∈[1,2,⋯,O],s∈[1,2,⋯,S+3]

3、构造高斯金字塔的示例

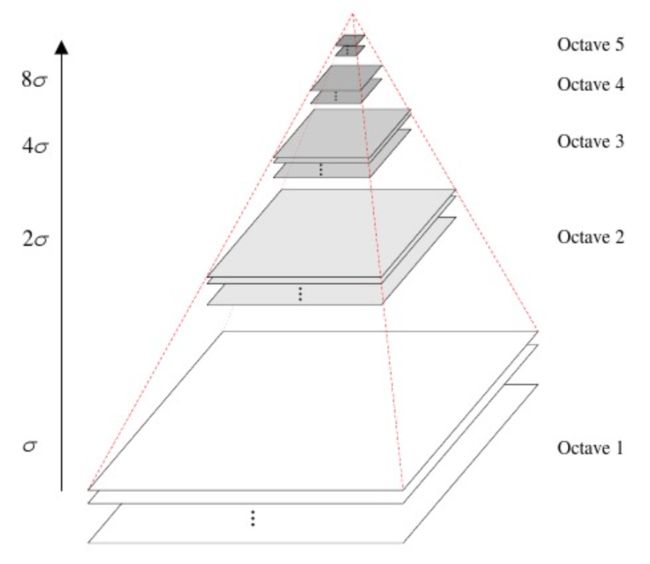
        设图像的尺寸为 256×256 ，则高斯金字塔的层数（Octave）为 log2256−3=5 。

        设 S=3 ，则每组需要 S+3=6 幅图像。

        设高斯金字塔第 i 组 (i=1,2,3,4,5) 的尺度为

G(i)=(σ(i)1,σ(i)2,σ(i)3,σ(i)4,σ(i)5,σ(i)6)

        DoG 金字塔第 i 组的尺度为

D(i)=(σ(i)1,σ(i)2,σ(i)3,σ(i)4,σ(i)5)

        极值点检测在第 i 组的尺度为

R(i)=(σ(i)2,σ(i)3,σ(i)4)

        由此可得（这里仅保留系数）

G(1)=(01,2013,2023,2033,2043,2053);D(1)=(01,2013,2023,2033,2043);R(1)=(2013,2023,2033)

G(2)=(02,2043,2053,2063,2073,2083);D(2)=(02,2043,2053,2063,2073);R(2)=(2043,2053,2063)

G(3)=(04,2073,2083,2093,2103,2113);D(3)=(04,2073,2083,2093,2103);R(3)=(2073,2083,2093)

G(4)=(08,2103,2113,2123,2133,2143);D(4)=(08,2103,2113,2123,2133);R(4)=(2103,2113,2123)

G(5)=(16,2133,2143,2153,2163,2173);D(5)=(16,2133,2143,2153,2163);R(5)=(2133,2143,2153)

        从上述结果可以看出，按照这种方式构造的高斯金字塔，在极值点检测时，其尺度变化确实是连续的。

4、其它

        利用高斯金字塔，对图像下采样的过程为：

        1）与高斯模板进行卷积

        2）去除偶数行和偶数列

        下采样会缩小图像，并且逐渐丢失图像信息。



        利用高斯金字塔，对图像上采样的过程为：

        1）在每个方向上扩大为原来的两倍，新增行列用0填充

        2）使用同样的高斯模板（数值上乘以4）与新的图像进行卷积

        上采样会放大图像，也会丢失信息，使图像变模糊。