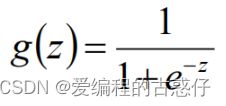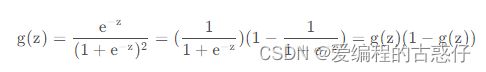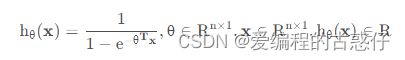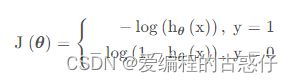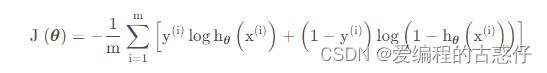2.2、logistic回归
一、什么是logistics回归
首先我们先要了解回归的概念,现有一些数据点,我们用 一条直线对这些点进行拟合,该线称为最佳拟合直线,这个拟合过程就称作回归。logistic回归虽然说是回归,但确是为了解决分类问题,是二分类任务的首选方法,简单来说,输出结果不是0就是1。
举个简单的例子:癌症检测——输入病理的图片并且辨别患者是否患有癌症
二、logistics回归和线性回归
线性回归:线性回归是机器学习中比较基本的一个算法。其基本思想大致可以理解为给定一个数据集,通过线性回归得到一条曲线,尽可能地去拟合这个数据集。
logistics回归:逻辑回归是以线性回归为理论支持的,但是逻辑回归通过Sigmoid函数引入了非线性因素,因此可以轻松处理0/1分类问题。
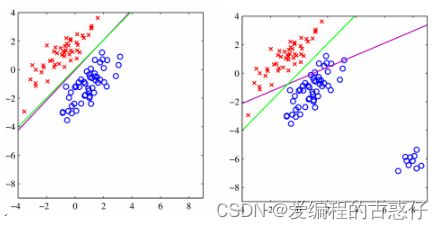
对于图二来说,在角落加上一块蓝色点之后,线性回归的线会向下倾斜,参考紫色的线。
logistic回归(参考绿色的线)分类的还是很准确,logistic回归在解决分类问题上还是不错的
三、logistic回归的原理
Sigmoid函数:
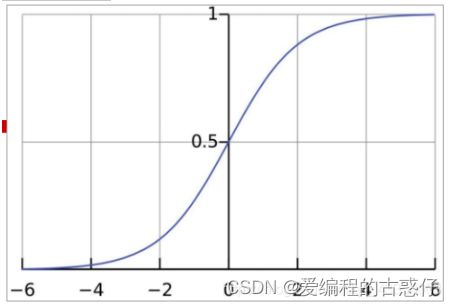
Sigmoid函数图像:
Sigmoid函数的导数为:
Logistic回归通过Sigmoid函数,输入拟合函数后,将输出值固定在[0,1]区间。所以我们可以将输出值视为概率值。通常情况下,当概率值小于0.5时,输出为0;当时概率值大于0.5时,输出为1:
四、logistic回归损失函数
如果logistic回归仍然采用和线性回归一样的代价函数,由于拟合函数的改变,会使最终的代价函数变为非凸的函数,从而无法很好地利用梯度下降法去求解。为此,在logistic回归中,代价函数变成了交叉熵损失函数:
为了简化公式,上述分段函数可以进一步写成:
于是,针对m个训练集,最终的代价函数为:
接下来的流程就和线性回归一致了,即利用梯度下降,通过多次迭代,最终得到一组合适的参数θ
五、项目举例
鸢尾分类
1、LogisticRegression 类
sklearn.linear_model.LogisticRegression (penalty='l2', *,
dual=False,
tol=0.0001, C=1.0,
fit_intercept=True,
intercept_scaling=1,
class_weight=None,
random_state=None,
solver='lbfgs',
max_iter=100,
multi_class='auto',
verbose=0,
warm_start=False,
n_jobs=None,
l1_ratio=None)
2、案例
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# 载入数据集,Y的值有0,1,2三种情况,每种特征150个样本
iris = load_iris()
X = iris.data[:, :2] #获取花卉两列数据集
Y = iris.target
# 对数据做一些格式转换
X=pd.DataFrame(X)
Y=pd.DataFrame(Y)
X.columns=["Sepal length","Sepal width"]
Y.columns=["class"]
print(X.head())
print(Y.head())
Y=Y.loc[:,"class"]
# 画出散点图,先看一下数据分布情况
setosa = plt.scatter(X.loc[:, "Sepal length"][Y == 0],
X.loc[:, "Sepal width"][Y == 0],
color='red', marker='o', label='setosa')
versicolor = plt.scatter(X.loc[:, "Sepal length"][Y == 1],
X.loc[:, "Sepal width"][Y == 1],
color='blue', marker='*', label='versicolor')
virginica = plt.scatter(X.loc[:, "Sepal length"][Y == 2],
X.loc[:, "Sepal width"][Y == 2],
color='yellow', marker='x', label='virginica')
plt.legend((setosa, versicolor, virginica),
('setosa', 'versicolor', 'virginica'))
plt.xlabel("Sepal length")
plt.ylabel("Sepal width")
plt.show()
# 建立逻辑回归模型,开始训练
lr = LogisticRegression()
lr = lr.fit(X,Y)
# 预测、计算分类准确度
y_pred= lr.predict(X)
print("准确结果")
print(accuracy_score(Y,y_pred))
print("---------------------------------------------")
# 打印出预测结果,以及逻辑回归得到的三条分界线的斜率和截距
print("预测结果为:")
print(y_pred)
print("---------------------------------------------")
print("逻辑回归得到的三条分界线的斜率为:")
print(lr.coef_)
print("---------------------------------------------")
print("逻辑回归得到的三条分界线的截距为:")
print(lr.intercept_)
#可视化分类结果
# 由函数关系在散点图上绘制出三条边界线,直观的看一下分类效果
# c+a*x1+b*x2=0
fig = plt.figure()
a1 = lr.coef_[0][0]
b1 = lr.coef_[0][1]
c1 = lr.intercept_[0]
a2 = lr.coef_[1][0]
b2 = lr.coef_[1][1]
c2 = lr.intercept_[1]
a3 = lr.coef_[2][0]
b3 = lr.coef_[2][1]
c3 = lr.intercept_[2]
x = X.loc[:, "Sepal length"]
y1 = -(c1 + a1 * x) / b1
y2 = -(c2 + a2 * x) / b2
y3 = -(c3 + a3 * x) / b3
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
setosa = plt.scatter(X.loc[:, "Sepal length"][Y == 0],
X.loc[:, "Sepal width"][Y == 0],
color='red', marker='o', label='setosa')
versicolor = plt.scatter(X.loc[:, "Sepal length"][Y == 1],
X.loc[:, "Sepal width"][Y == 1],
color='blue', marker='*', label='versicolor')
virginica = plt.scatter(X.loc[:, "Sepal length"][Y == 2],
X.loc[:, "Sepal width"][Y == 2],
color='yellow', marker='x', label='virginica')
plt.legend((setosa, versicolor, virginica),
('setosa', 'versicolor', 'virginica'))
plt.xlabel("Sepal length")
plt.ylabel("Sepal width")
plt.xlim((4, 8))
plt.ylim((2, 4.5))
plt.show()