机器学习可解释性之shap模块的使用——基础用法(一)
文章目录
- 【用Shapely解释机器学习模型】
-
- 1. 用Shapely解释线性模型
-
- 1.1 传统特征系数计算
- 1.2 部分特征依赖图(partial dependence plots)
- 1.3 瀑布图(waterfall plot)
- 2. 用Shapely解释加法回归模型
-
- 2.1 基础解释图(局部依赖、依赖关系散点图、瀑布图)
- 2.2 蜂群图(beeswarm)
- 3. 用Shapely解释非加法性质的提升树模型
-
- 3.1 基础解释图(部分依赖图、依赖关系图)
- 3.2 带SHAP值的依赖关系图
- 4. 用Shapely解释线性逻辑回归分类模型
-
- 4.1 基础解释图(局部依赖、依赖关系图)
- 4.2 引入log的线性依赖关系图
- 5. 用Shapely解释非加法性质的提升树逻辑回归模型
-
- 5.1 特征重要性
-
- 5.1.1 特征重要性条形图(SHAP平均绝对值)
- 5.1.2 特征重要性条形图(SHAP最大绝对值)
- 5.2 蜂群图
-
- 5.2.1 基础蜂群图
- 5.2.2 绝对值蜂群图(配色更改)
- 5.3 热力图
- 5.4 散点图
-
- 5.4.1 基础散点图(依赖关系图)
- 5.4.2 散点图(根据SHAP值分配颜色)
- 5.4.3 散点图(根据其他特征SHAP值分配颜色)
- 5.5 特征聚类相关性条形图
之前对模型可解释性有相关的讨论: 模型树结构的可视化、特征重要性
本文主要是总结shap对模型进行可解释性分析时的使用方式与含义,简单来说就是把官方文档翻译一遍: Shap模块官方文档
安装命令如下:
# pip下载
pip3 install shap
# conda环境下载
conda install -c conda-forge shap
本文使用shap版本为0.39.0,所展示的案例中要导入的所有的包如下:
import shap
import sklearn
import matplotlib.pyplot as plt
import interpret.glassbox
import xgboost
import pandas as pd
import transformers
import datasets
import torch
import numpy as np
import scipy as sp
【用Shapely解释机器学习模型】
1. 用Shapely解释线性模型
1.1 传统特征系数计算
# 经典波士顿住房价格预测数据集
data_df, label_array = shap.datasets.boston()
print(list(data_df.columns))
"""
数据集中的所有特征名称
['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
"""
# 获取100个样本数据进行可解释性分析
X100 = shap.utils.sample(data_df, 100)
# 线性模型训练
model = sklearn.linear_model.LinearRegression()
model.fit(data_df, label_array)
# 观察训练好的线性模型中不同特征的系数取值
print("Model coefficients:\n")
for i in range(data_df.shape[1]):
print(data_df.columns[i], "=", model.coef_[i].round(5))
"""
Model coefficients:
CRIM = -0.10801
ZN = 0.04642
INDUS = 0.02056
CHAS = 2.68673
NOX = -17.76661
RM = 3.80987
AGE = 0.00069
DIS = -1.47557
RAD = 0.30605
TAX = -0.01233
PTRATIO = -0.95275
B = 0.00931
LSTAT = -0.52476
"""
1.2 部分特征依赖图(partial dependence plots)
shap.partial_dependence_plot(
ind="CRIM", model=model.predict,
data=X100, ice=False,
model_expected_value=True,
feature_expected_value=True
)
# 若不想展示图像,可修改如下
# shap.partial_dependence_plot(
# "CRIM", model.predict, X100, ice=False,
# model_expected_value=True, feature_expected_value=True,
# show=False
# )
# plt.savefig("partial_dependence_plot.png")
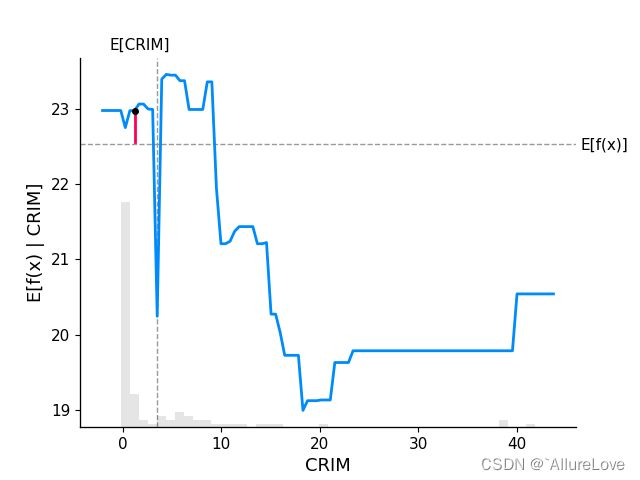
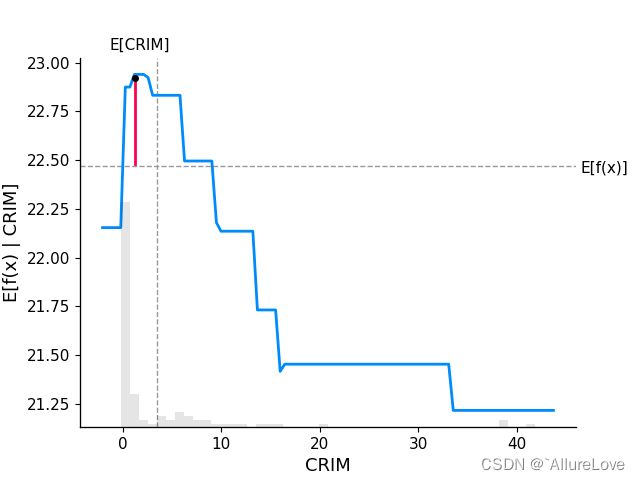
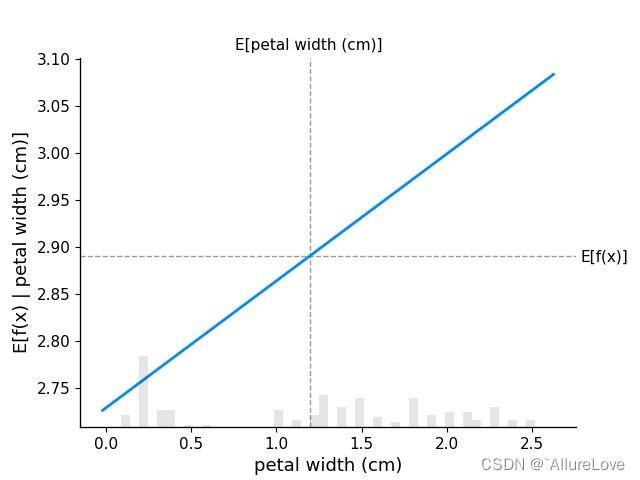
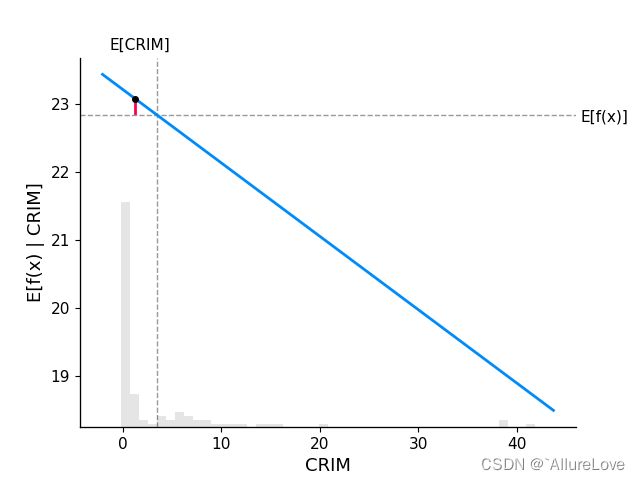
如图所示,其中 E [ f ( x ) ] E[f(x)] E[f(x)]对应的 灰色横线表示的是模型对波士顿房价预测的期望值,垂直的灰色线条表示的是特征CRIM的平均取值,蓝色的线表示的是模型预测结果的平均值随特征CRIM平均取值的变化,从图中可以看出也就意味着CRIM平均取值越大,预测的数值平均会越小,二者相交的点为依赖中心。灰色的条形图则表示参与模型可解释性的样本的数据分布。

对线性预测模型 f ( x ) f(x) f(x)进行可解释性分析时,对于特定特征 C R I M CRIM CRIM而言其对应的shap值为在特征 i i i取值下的样本 x C R I M = 特定值 x_{CRIM=特定值} xCRIM=特定值的模型预测数值 f ( x C R I M = 特定值 ) f(x_{CRIM=特定值}) f(xCRIM=特定值)和部分特征依赖图中对应的期望预测均值 E ( f ( x ) ∣ C R I M = 特定值 ) E(f(x)|_{CRIM=特定值}) E(f(x)∣CRIM=特定值)的差值,即: s i n g l e _ s h a p C R I M = f ( x C R I M = 特定值 ) − E ( f ( x ) ∣ C R I M = 特定值 ) single\_shap_{CRIM}=f(x_{CRIM=特定值})-E(f(x)|{CRIM=特定值}) single_shapCRIM=f(xCRIM=特定值)−E(f(x)∣CRIM=特定值)
# 计算线性模型对应的shap值
explainer = shap.Explainer(model.predict, X100)
shap_values = explainer(data_df)
# 绘制标准部分特征依赖图
sample_ind = 20 # 选取一个样本,样本索引
shap.partial_dependence_plot(
ind="CRIM", model=model.predict,
data=X100, ice=False,
model_expected_value=True,
feature_expected_value=True,
shap_values=shap_values[sample_ind:sample_ind+1, :]
)
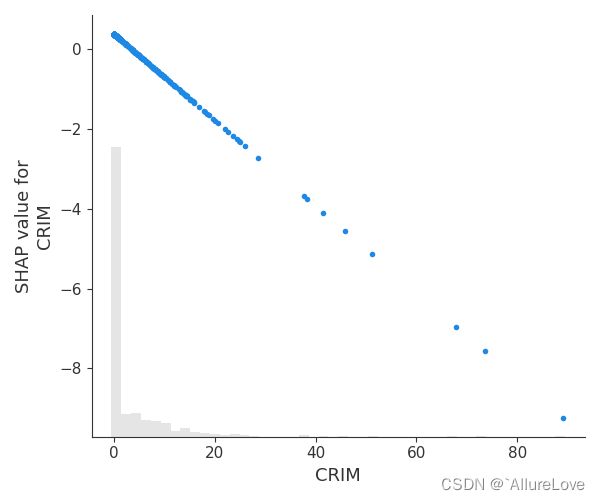
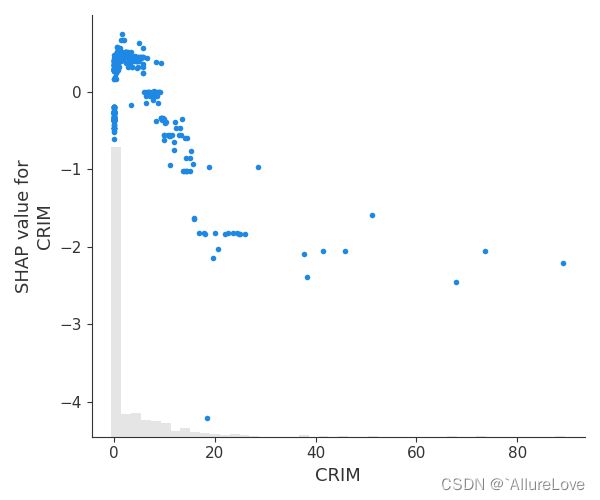
shap值和部分特征依赖图之间联系紧密,因此如果能够在数据集中绘制特定特征对应的shap值,就能够很快解析出该特征对应的部分特征依赖图的依赖中心
# 观察CRIM特征对应的shap值随CRIM取值的变化
shap.plots.scatter(shap_values[:, "CRIM"], show=False) # show设置成False
plt.tight_layout() # 解决图片显示不完整的问题
plt.show()
1.3 瀑布图(waterfall plot)
shap值计算过程中的一个基本属性是,对所有特征而言,其shap取值总是多有样本对应的期望预测结果和当前预测结果之差的总和,即: t o t a l _ s h a p C R I M = ∑ ( f ( x C R I M = 特定值 ) − E [ f ( x ) ∣ C R I M = 特定值 ] ) total\_shap_{CRIM}=\sum(f(x_{CRIM=特定值})-E[f(x)|CRIM=特定值]) total_shapCRIM=∑(f(xCRIM=特定值)−E[f(x)∣CRIM=特定值]) 特定值 ∈ 数据集中 C R I M 的取值集合 特定值\in 数据集中CRIM的取值集合 特定值∈数据集中CRIM的取值集合
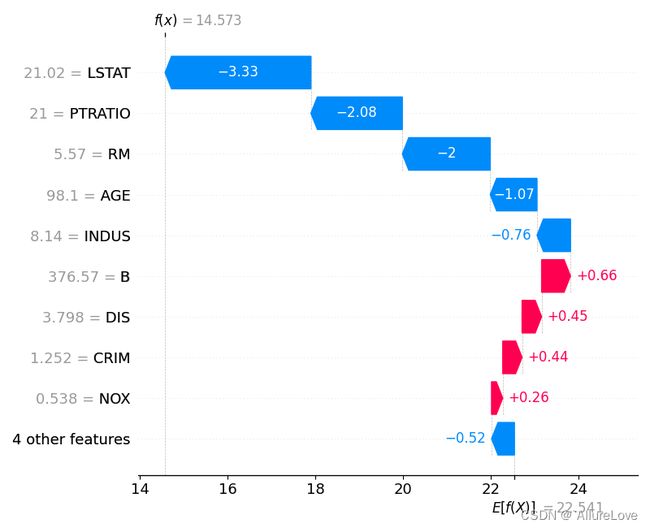
对于从样本期望输出值 E [ f ( x ) ] E[f(x)] E[f(x)]而言,要得到模型预测的输出结果 f ( x ) f(x) f(x),需要逐步增加其他特征,使得期望输出不断靠近预测结果,瀑布图就能够清楚的展示该过程
# 选中的样本
sample_ind = 20
# max_display表示最多个特征
plt.subplots(constrained_layout=True) # 图片显示不全时的另一个解决方法
shap.plots.waterfall(shap_values[sample_ind], max_display=14)
2. 用Shapely解释加法回归模型
线性模型的部分依赖图之所以与SHAP值有如此密切的联系,是因为在线性模型中每个特征都是独立进行处理的(最终效果是加在一起)。可以在放宽直线的线性要求的同时保留这种加法特性,从而就衍生出了很多广义上的加法模型(Generalized Additive Models, GAMs),如:深度为1的XGBOOST。在shap模块中,专门为广义的模型设计了 InterpretMLs explainable boosting machines(可解释性提升机器?),用于解释更宽泛的预测模型
2.1 基础解释图(局部依赖、依赖关系散点图、瀑布图)
# 训练广义加法模型
model_ebm = interpret.glassbox.ExplainableBoostingRegressor(interactions=0)
model_ebm.fit(data_df, label_array)
# 用SHAP解释GAMs
explainer_ebm = shap.Explainer(model_ebm.predict, X100)
shap_values_ebm = explainer_ebm(data_df)
sample_ind = 20
# 绘制标准的局部依赖图
fig, ax = shap.partial_dependence_plot(
ind="CRIM", model=model_ebm.predict, data=X100,
model_expected_value=True, feature_expected_value=True, ice=False,
shap_values=shap_values_ebm[sample_ind:sample_ind + 1, :]
)
# 绘制SHAP值和特征取值之间的关系图
shap.plots.scatter(shap_values_ebm[:, "CRIM"], show=False)
plt.tight_layout()
plt.show()
# 针对某个样本绘制其对应瀑布图
shap.plots.waterfall(shap_values_ebm[sample_ind], show=False)
plt.tight_layout()
plt.show()
2.2 蜂群图(beeswarm)
# 为所有的样本绘制蜂群图
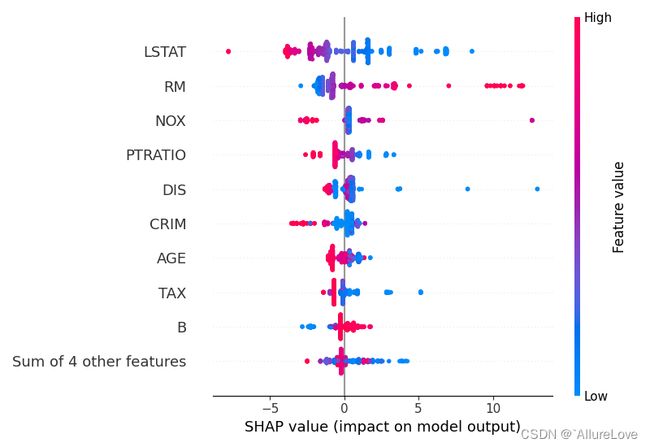
shap.plots.beeswarm(shap_values_ebm, show=False)
plt.tight_layout()
plt.show()
蜂群图可以反映各个特征取值的高低对SHAP取值的影响(结合上述对SHAP的解释,SHAP值的绝对值越大表明期望输出和真实输出的差异越大),就可以看到特征对模型预测的影响
3. 用Shapely解释非加法性质的提升树模型
3.1 基础解释图(部分依赖图、依赖关系图)
# 训练XGBOOST模型
model_xgb = xgboost.XGBRegressor(n_estimators=100, max_depth=2).fit(data_df, label_array)
# 解释该模型
explainer_xgb = shap.Explainer(model_xgb, X100)
shap_values_xgb = explainer_xgb(data_df)
sample_ind = 20
# 绘制局部依赖图
fig, ax = shap.partial_dependence_plot(
ind="CRIM", model=model_xgb.predict, data=X100,
model_expected_value=True,
feature_expected_value=True, ice=False,
shap_values=shap_values_xgb[sample_ind:sample_ind + 1, :]
)
# 绘制依赖关系散点图
shap.plots.scatter(shap_values_xgb[:, "CRIM"], show=False)
plt.tight_layout()
plt.show()
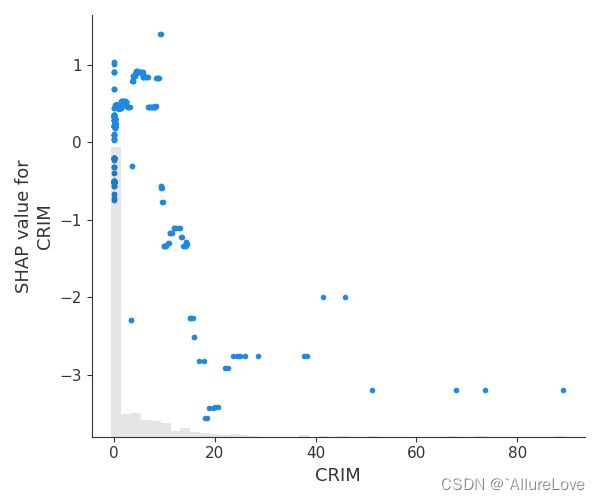
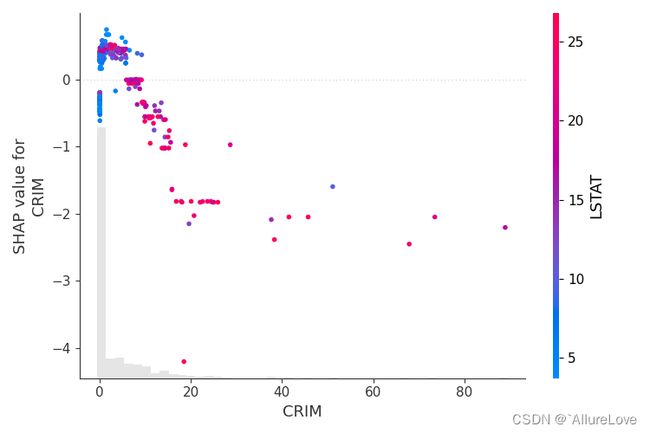
3.2 带SHAP值的依赖关系图
# 加入SHAP值细节绘制依赖关系散点图
shap.plots.scatter(shap_values_xgb[:, "CRIM"], color=shap_values_xgb, show=False)
plt.tight_layout()
plt.show()
4. 用Shapely解释线性逻辑回归分类模型
4.1 基础解释图(局部依赖、依赖关系图)
# 经典鸢尾花分类数据集
X_iris, y_iris = shap.datasets.iris()
print(list(X_iris.columns))
# 简单的线性逻辑回归模型
model_iris = sklearn.linear_model.LogisticRegression(max_iter=10000)
model_iris.fit(X_iris, y_iris)
def model_iris_proba(x):
return model_iris.predict_proba(x)[:, 1]
def model_iris_log_odds(x):
p = model_iris.predict_log_proba(x)
return p[:, 1] - p[:, 0]
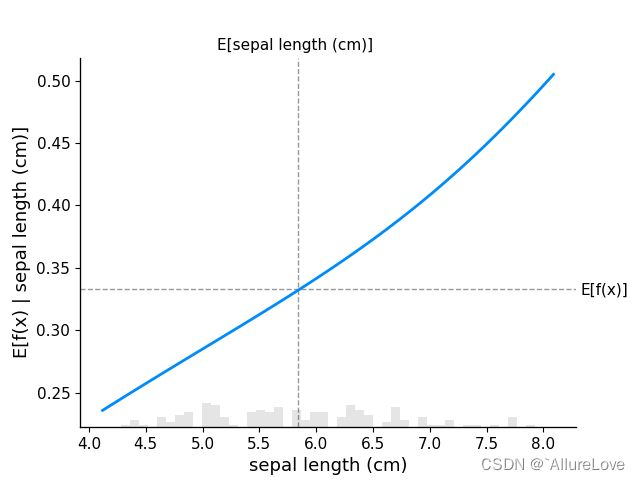
# 绘制标准的局部依赖图
sample_ind = 18
fig, ax = shap.partial_dependence_plot(
ind="sepal length (cm)", model=model_iris_proba,
data=X_iris, model_expected_value=True,
feature_expected_value=True, ice=False
)
# 计算shap值
background_iris = shap.maskers.Independent(X_iris, max_samples=100)
explainer = shap.Explainer(model_iris_proba, background_iris)
shap_values_iris = explainer(X_iris[:1000])
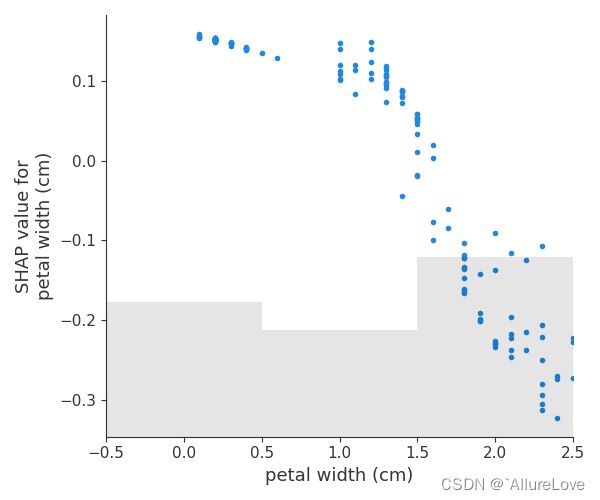
# 绘制关系依赖图
shap.plots.scatter(shap_values_iris[:, "petal width (cm)"], show=False)
plt.tight_layout()
plt.show()
4.2 引入log的线性依赖关系图
# 计算log-odds就可以观察输入输出之间的线性关系
explainer_log_odds = shap.Explainer(model_iris_log_odds, background_iris)
shap_values_iris_log_odds = explainer_log_odds(X_iris[:1000])
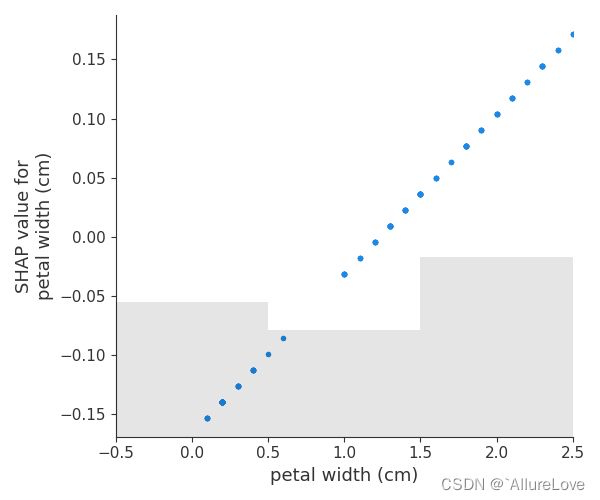
# 绘制关系依赖图
shap.plots.scatter(shap_values_iris_log_odds[:, "petal width (cm)"], show=False)
plt.tight_layout()
plt.show()
# 绘制标准的部分依赖图
sample_ind = 18
fig, ax = shap.partial_dependence_plot(
"petal width (cm)", model_iris_log_odds, X_iris, model_expected_value=True,
feature_expected_value=True, ice=False
)
5. 用Shapely解释非加法性质的提升树逻辑回归模型
adult数据集下载
数据集预处理参考
5.1 特征重要性
5.1.1 特征重要性条形图(SHAP平均绝对值)
columns = ['Age', 'Workclass', 'fnlgwt', 'Education', 'EdNum', 'MaritalStatus',
'Occupation', 'Relationship', 'Race', 'Sex', 'CapitalGain',
'CapitalLoss', 'HoursPerWeek', 'Country', 'Income']
# 根据链接下载adult数据集(load不出来总是网络错误。。。只能把数据集下载下来,效果差不多应该。。)
adult_df = pd.read_csv("adult.data", names=columns)
def data_process(df):
"""
处理数据集的函数
:param df:
:param model:
:return:
"""
df.replace(" ?", pd.NaT, inplace=True)
df.replace(" >50K", 1, inplace=True)
df.replace(" <=50K", 0, inplace=True)
trans = {'Workclass': df['Workclass'].mode()[0], 'Occupation': df['Occupation'].mode()[0],
'Country': df['Country'].mode()[0]}
df.fillna(trans, inplace=True)
df.drop('fnlgwt', axis=1, inplace=True)
df.drop('CapitalGain', axis=1, inplace=True)
df.drop('CapitalLoss', axis=1, inplace=True)
df_object_col = [col for col in df.columns if df[col].dtype.name == 'object']
df_int_col = [col for col in df.columns if df[col].dtype.name != 'object' and col != 'Income']
target = df["Income"]
dataset = pd.concat([df[df_int_col], pd.get_dummies(df[df_object_col])], axis=1)
return dataset, target
# 获取处理后的数据集合
X_adult, y_adult = data_process(adult_df)
# 加载二分类糖尿病数据集
print(list(X_adult.columns))
# 训练XGBoost模型
# n_estimators=5设置的比较小,为了省时
xgb_adult = xgboost.XGBClassifier(n_estimators=5, max_depth=2).fit(X_adult, y_adult * 1, eval_metric="logloss")
# 计算SHAP values
background_adult = shap.maskers.Independent(X_adult, max_samples=100)
explainer = shap.Explainer(xgb_adult, background_adult)
shap_values = explainer(X_adult)
# 设置用于绘图的数据,又超时。。
# shap_values.display_data = shap.datasets.adult(display=True)[0].values
# 绘制特征条形图
shap.plots.bar(shap_values, show=False)
plt.tight_layout()
plt.show()
特征条形图反应了特征与SHAP平均绝对值之间的关系,也就从全局反应了特征重要性的排名

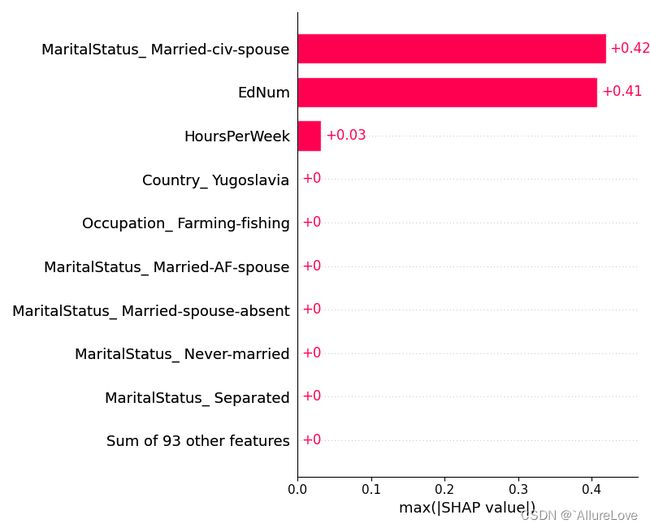
5.1.2 特征重要性条形图(SHAP最大绝对值)
# 绘制最大绝对值与特征之间的关系,另一种方式衡量特征重要性
shap.plots.bar(shap_values.abs.max(0), show=False)
plt.tight_layout()
plt.show()
5.2 蜂群图
5.2.1 基础蜂群图
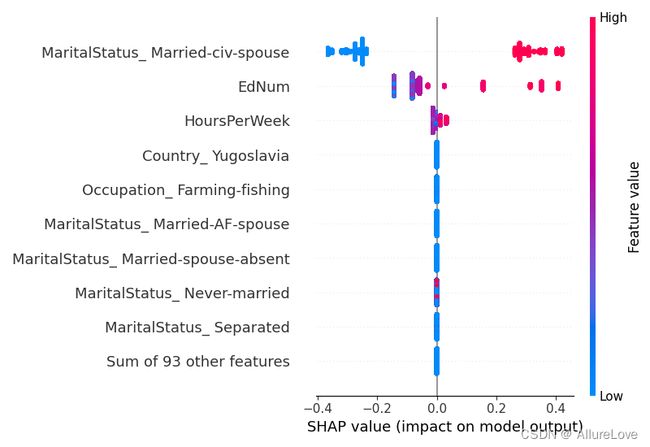
shap.plots.beeswarm(shap_values, show=False)
plt.tight_layout()
plt.show()
5.2.2 绝对值蜂群图(配色更改)
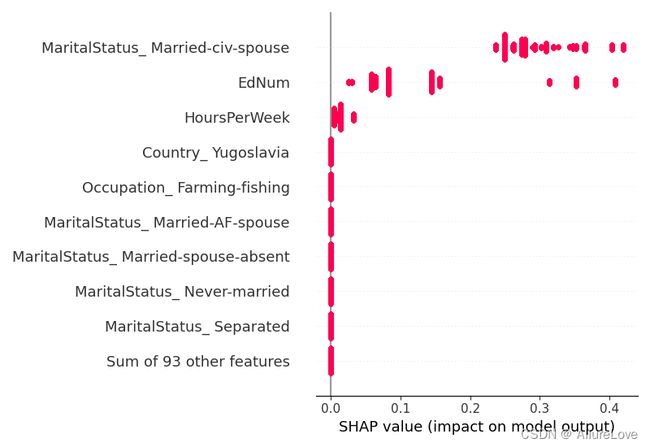
shap.plots.beeswarm(shap_values.abs, color="shap_red", show=False)
plt.tight_layout()
plt.show()
绝对值蜂群图是蜂群图和条形图的折中,复杂度适中,也能反应特征的重要性
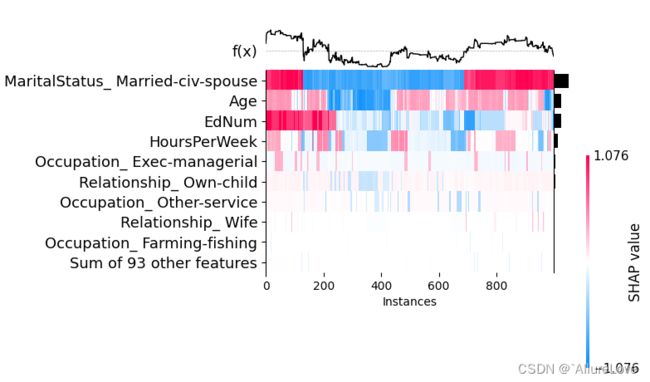
5.3 热力图
# 为了更好地观察结果n_estimators更新为50
shap.plots.heatmap(shap_values[:1000], show=False)
plt.tight_layout()
plt.show()
5.4 散点图
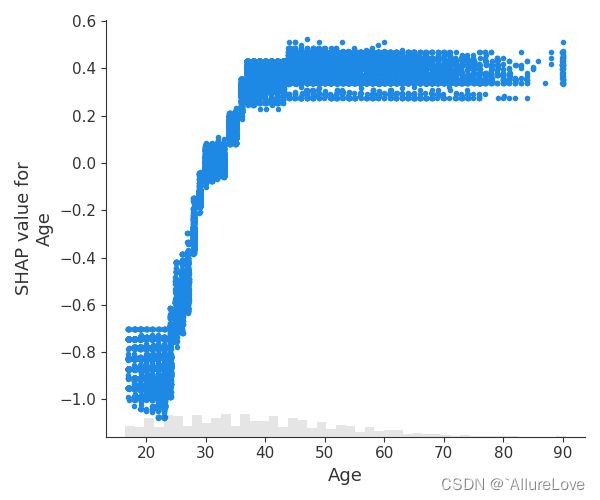
5.4.1 基础散点图(依赖关系图)
shap.plots.scatter(shap_values[:, "Age"], show=False)
plt.tight_layout()
plt.show()
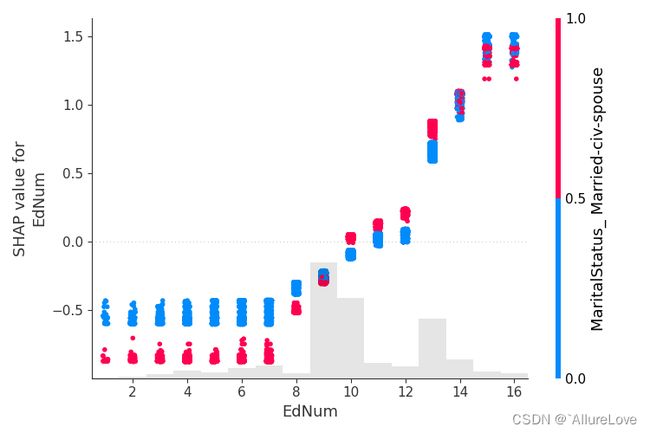
shap.plots.scatter(shap_values[:, "EdNum"], color=shap_values, show=False)
plt.tight_layout()
plt.show()
5.4.2 散点图(根据SHAP值分配颜色)
shap.plots.scatter(shap_values[:, "Age"], color=shap_values, show=False)
plt.tight_layout()
plt.show()
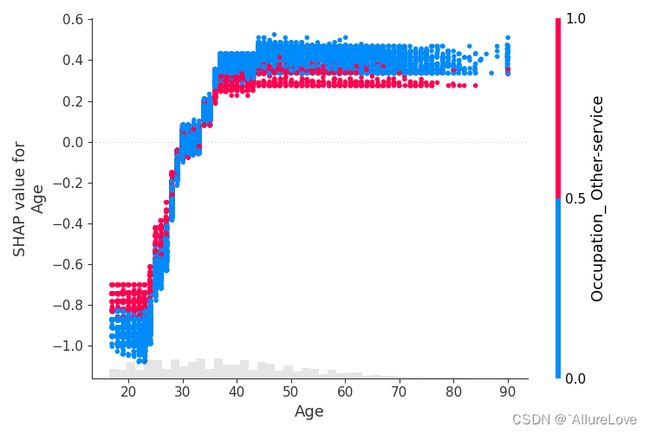
5.4.3 散点图(根据其他特征SHAP值分配颜色)
shap.plots.scatter(shap_values[:, "Age"], color=shap_values[:, "HoursPerWeek"], show=False)
plt.tight_layout()
plt.show()
5.5 特征聚类相关性条形图
# 进行特征聚类
clustering = shap.utils.hclust(X_adult, y_adult)
# 根据聚类后的数据进行可解释性分析
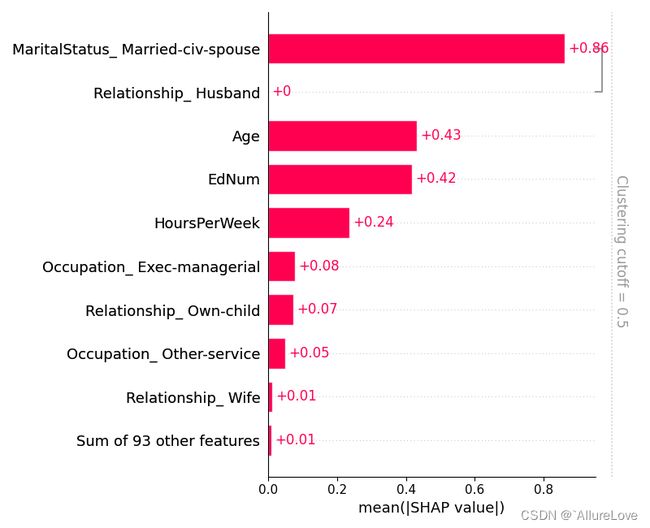
shap.plots.bar(shap_values, clustering=clustering, show=False)
plt.tight_layout()
plt.show()
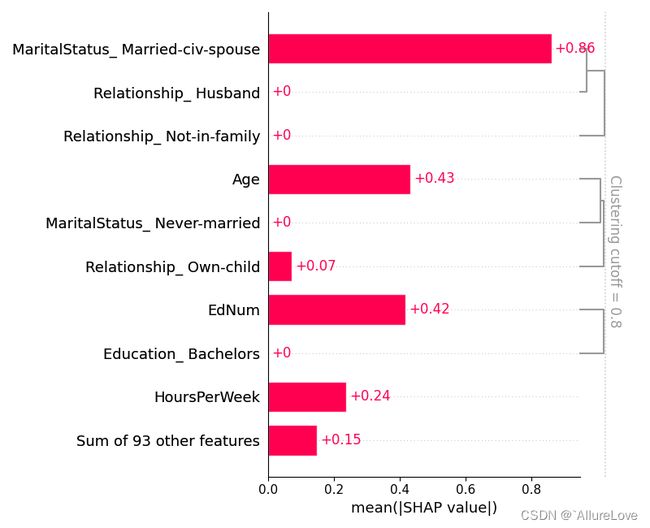
# 设置cutoff参数观察不同特征之间的相关性
shap.plots.bar(shap_values, clustering=clustering, clustering_cutoff=0.8, show=False)
plt.tight_layout()
plt.show()