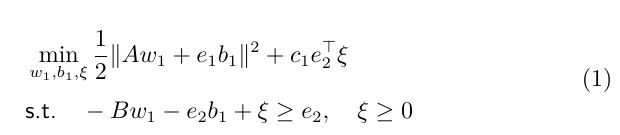双平面支持向量机(TSVM)对偶问题的推导
双平面支持向量机对偶问题推导及相关介绍
- TSVM相关介绍
- 第一个平面对偶问题的推导
- 第二个平面对偶问题的推导
- 双平面支持向量机的Matlab代码实现二分类
TSVM相关介绍
在双平面支持向量机中,我们希望找到两个非平行的超平面,使得其中的一个平面距离某一类比较近而离另外一类尽可能的远,其结构如下图所示,其中圆是一类样本,三角形的是另外一类样本

第一个平面对偶问题的推导
其中 A A A是正类样本组成的样本矩阵, B B B是负类样本组成的样本矩阵, w 1 , w 2 w_1,w_2 w1,w2分别是要找到的两个平面的法向量, b 1 , b 2 b_1,b_2 b1,b2是对应的偏置, ξ \xi ξ是松弛变量, c 1 c_1 c1是需要调整的超参数, e 1 , e 2 e_1,e_2 e1,e2是分别与正负样本数量对应的数值全1的列向量
引入拉格朗日乘子,得到方程(1)对应的拉格朗日函数为:
 其中 α , β \alpha,\beta α,β是拉格朗日乘子, 根据KKT条件,我们有:
其中 α , β \alpha,\beta α,β是拉格朗日乘子, 根据KKT条件,我们有:

为了表示方便,我们令: G = [ A e 1 ] , H = [ B e 2 ] , u 1 = [ w 1 b 1 ] , u 2 = [ w 2 b 2 ] G = [A\,\,\, e_1], H = [B\,\,\, e_2], u_1 = [w_1\,\,\, b_1], u_2 = [w_2\,\,\, b_2] G=[Ae1],H=[Be2],u1=[w1b1],u2=[w2b2]
由 ① + ② ①+② ①+②得:
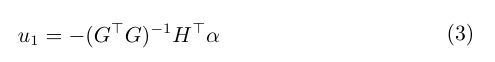
由 ③ ③ ③得:
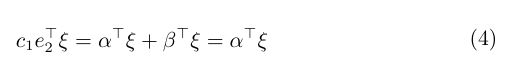
由 ④ ④ ④得

在方程(4)和方程(5)中,我们都得到了 α ⊤ ξ \alpha^\top \xi α⊤ξ的表达式,使用 α ⊤ B w 1 + α ⊤ e 2 b 1 + α ⊤ e 2 \alpha ^\top Bw_1+\alpha^\top e_2b_1+\alpha^\top e_2 α⊤Bw1+α⊤e2b1+α⊤e2来代替 c 1 e 2 ⊤ ξ c_1e_2^\top \xi c1e2⊤ξ并将其带入到方程(1)中,我们有:
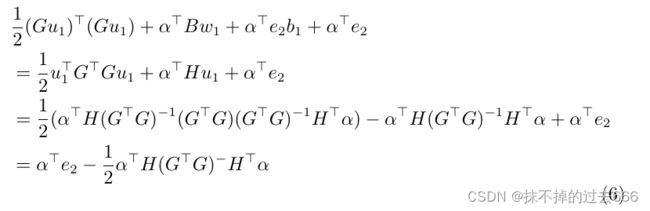
则我们可以得到方程(1)对应的对偶式为:

而上述式子是一个标准的二次规划问题,我们可以通过二次规划的工具包来对 α \alpha α进行求解,在求解出 α \alpha α后,可对 u 1 u_1 u1进行更新:
![]()
但是 G ⊤ G G^\top G G⊤G有可能不是满秩的,即其逆无法直接求解出来,所以我们一般可以给其再添加上一个比较小的数再求解其逆,如:

其中 δ \delta δ是一个比较小的数, I I I是单位阵
第二个平面对偶问题的推导
同理,我们的第二个平面也是使用类似的推导过程来进行获取,有:
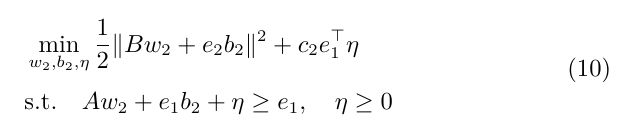
引入拉格朗日乘子,方程(10)对应的拉格朗日函数为:

其中 γ , ζ \gamma,\zeta γ,ζ是拉格朗日乘子,根据KKT条件,我们有:
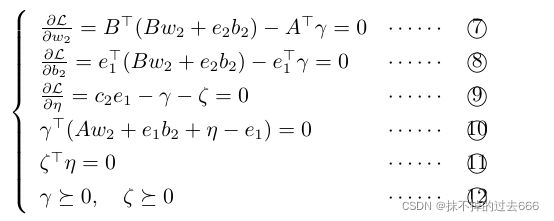
由 ⑦ + ⑧ ⑦+⑧ ⑦+⑧得:

由 ⑨ ⑨ ⑨得:
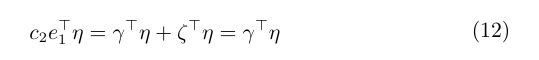
由 ⑩ ⑩ ⑩得
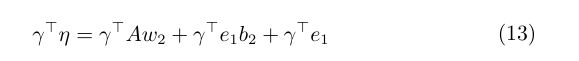
即我们可以使用 γ ⊤ A w 2 + γ ⊤ e 1 b 2 + γ ⊤ e 1 \gamma ^\top Aw_2+\gamma^\top e_1b_2+\gamma^\top e_1 γ⊤Aw2+γ⊤e1b2+γ⊤e1来代替 c 2 e 1 ⊤ η c_2e_1^\top \eta c2e1⊤η,将其带入到方程(10)中,我们有

得到方程(10)对应的对偶式为:

方程(15)同样是一个标准的二次规划问题,可以使用工具包来求解得到拉格朗日乘子向量 γ \gamma γ,在求解出 γ \gamma γ后,可对 u 2 u_2 u2进行更新:

同理,为避免 ( H ⊤ H ) (H^\top H) (H⊤H)不满秩的情况,我们给其对角位置添加上一个比较小的数有:
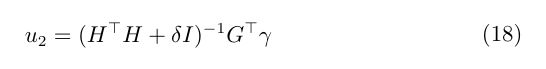
其中 δ \delta δ是一个比较小的实数, I I I是单位阵,于是我们可以得到 u 1 , u 2 u_1,u_2 u1,u2的更新式
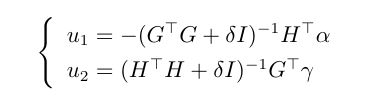
当在训练集上训练完毕,当测试集数据 x ∈ R d x \in \mathcal{R}^d x∈Rd来到的时候,我们有:

当 f ( x ) > 0 f(x) > 0 f(x)>0时,将其分配到“-1”类,当 f ( x ) < 0 f(x) < 0 f(x)<0时,将其分配到“+1”类
双平面支持向量机的Matlab代码实现二分类
主函数代码,其中需要传入三个参数,TestX是测试数据,DataTrain是训练数据,其有 A , B A,B A,B两个成员,分别是正负样本,FunPara传入需要的参数, c 1 , c 2 c_1,c_2 c1,c2以及 δ \delta δ
function Predict_Y = TWSVM(TestX,DataTrain,FunPara)
Xpos = DataTrain.A;
Xneg = DataTrain.B;
cpos = FunPara.c1;
cneg = FunPara.c2;
eps1 = FunPara.c3;
eps2 = FunPara.c4;
kerfPara = FunPara.kerfPara;
m1=size(Xpos,1);
m2=size(Xneg,1);
e1=-ones(m1,1);
e2=-ones(m2,1);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Compute Kernel
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if strcmp(kerfPara.type,'lin')
H=[Xpos,-e1];
G=[Xneg,-e2];
else
X=[DataTrain.A;DataTrain.B];
H=[kernelfun(Xpos,kerfPara,X),-e1];
G=[kernelfun(Xneg,kerfPara,X),-e2];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Compute (w1,b1) and (w2,b2)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%DTWSVM1
HH=H'*H;
HH = HH + eps1*eye(size(HH));%regularization
HHG = HH\G';
kerH1=G*HHG;
kerH1=(kerH1+kerH1')/2;
alpha=qpSOR(kerH1,0.5,cpos,0.05); %SOR
vpos=-HHG*alpha;
%%%%DTWSVM2 equ(29)
QQ=G'*G;
QQ=QQ + eps2*eye(size(QQ));%regularization
QQP=QQ\H';
kerH1=H*QQP;
kerH1=(kerH1+kerH1')/2;
gamma=qpSOR(kerH1,0.5,cneg,0.05);
vneg=QQP*gamma;
clear kerH1 H G HH HHG QQ QQP;
w1=vpos(1:(length(vpos)-1));
b1=vpos(length(vpos));
w2=vneg(1:(length(vneg)-1));
b2=vneg(length(vneg));
%toc;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Predict and output
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
m=size(TestX,1);
if strcmp(kerfPara.type,'lin')
H=TestX;
w11=sqrt(w1'*w1);
w22=sqrt(w2'*w2);
y1=H*w1+b1*ones(m,1);
y2=H*w2+b2*ones(m,1);
else
C=[DataTrain.A;DataTrain.B];
H=kernelfun(TestX,kerfPara,C);
w11=sqrt(w1'*kernelfun(X,kerfPara,C)*w1);
w22=sqrt(w2'*kernelfun(X,kerfPara,C)*w2);
y1=H*w1+b1*ones(m,1);
y2=H*w2+b2*ones(m,1);
end
wp=sqrt(2+2*w1'*w2/(w11*w22));
wm=sqrt(2-2*w1'*w2/(w11*w22));
clear H; clear C;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
m1=y1/w11;
m2=y2/w22;
MP=(m1+m2)/wp;
MN=(m1-m2)/wm;
mind=min(abs(MP),abs(MN));
maxd=max(abs(MP),abs(MN));
Predict_Y = sign(abs(m2)-abs(m1));
end
function bestalpha=qpSOR(Q,t,C,smallvalue)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% NSVM: Nonparallel support vector machine
%
% bestalpha=qpSOR(Q,t,C,smallvalue)
%
% Input:
% Q - Hessian matrix(Require positive definite).
%
% t - (0,2) Paramter to control training.
%
% C - Upper bound
%
% smallvalue - Termination condition
%
% Output:
% bestalpha - Solutions of QPPs.
%
%Reference:
% Yuan-Hai Shao, Wei-Jie Chen and Nai-Yang Deng, "Nonparallel support
% vector machine" Submitted 2013
%
% version 1.0 --Apr/2013
%
% Written by Wei-Jie Chen (wjcper2008@126.com)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Initailization
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[m,n]=size(Q);
alpha0=zeros(m,1);
L=tril(Q);
E=diag(Q);
twinalpha=alpha0;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Compute alpha
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for j=1:n
% i=i+1;
twinalpha(j,1)=alpha0(j,1)-(t/E(j,1))*(Q(j,:)*twinalpha(:,1)-1+L(j,:)*(twinalpha(:,1)-alpha0));
if twinalpha(j,1)<0
twinalpha(j,1)=0;
elseif twinalpha(j,1)>C
twinalpha(j,1)=C;
else
;
end
end
alpha=[alpha0,twinalpha];
while norm(alpha(:,2)-alpha(:,1))>smallvalue
for j=1:n
twinalpha(j,1)=alpha(j,2)-(t/E(j,1))*(Q(j,:)*twinalpha(:,1)-1+L(j,:)*(twinalpha(:,1)-alpha(:,2)));
if twinalpha(j,1)<0
twinalpha(j,1)=0;
elseif twinalpha(j,1)>C
twinalpha(j,1)=C;
else
;
end
end
alpha(:,1)=[];
alpha=[alpha,twinalpha];
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Output
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
bestalpha=alpha(:,2);
计算核矩阵
function omega = kernelfun(Xtrain,kerfPara,Xt)
% Construct the positive (semi-) definite and symmetric kernel matrix
%
% >> Omega = kernelfun(X, kernel_fct, sig2)
%
% This matrix should be positive definite if the kernel function
% satisfies the Mercer condition. Construct the kernel values for
% all test data points in the rows of Xt, relative to the points of X.
%
% >> Omega_Xt = kernelfun(X, kernel_fct, sig2, Xt)
%
%
% Full syntax
%
% >> Omega = kernelfun(X, kernel_fct, sig2)
% >> Omega = kernelfun(X, kernel_fct, sig2, Xt)
%
% Outputs
% Omega : N x N (N x Nt) kernel matrix
% Inputs
% X : N x d matrix with the inputs of the training data
% kernel : Kernel type (by default 'RBF_kernel')
% sig2 : Kernel parameter (bandwidth in the case of the 'RBF_kernel')
% Xt(*) : Nt x d matrix with the inputs of the test data
kernel_type = kerfPara.type;
kernel_pars = kerfPara.pars;
nb_data = size(Xtrain,1);
if strcmp(kernel_type,'rbf'),
if nargin<3,
XXh = sum(Xtrain.^2,2)*ones(1,nb_data);
omega = XXh+XXh'-2*(Xtrain*Xtrain');
omega = exp(-omega./(2*kernel_pars(1)));
else
omega = - 2*Xtrain*Xt';
Xtrain = sum(Xtrain.^2,2)*ones(1,size(Xt,1));
Xt = sum(Xt.^2,2)*ones(1,nb_data);
omega = omega + Xtrain+Xt';
omega = exp(-omega./(2*kernel_pars(1)));
end
elseif strcmp(kernel_type,'lin')
if nargin<3,
omega = Xtrain*Xtrain';
else
omega = Xtrain*Xt';
end
elseif strcmp(kernel_type,'poly')
if nargin<3,
omega = (Xtrain*Xtrain'+kernel_pars(1)).^kernel_pars(2);
else
omega = (Xtrain*Xt'+kernel_pars(1)).^kernel_pars(2);
end
end