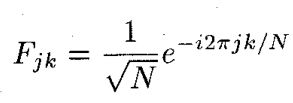分数阶傅里叶变换(FrFT)详细原理与matlab代码实现
本文主要是基于Haldun M. Ozaktas, Orhan等人的论文Digital Computation of the Fractional Fourier Transform 翻译而成。如有错误之处还请指出。
摘要
本文给出了一种高效、精确计算分数傅里叶变换的算法。对于时间带宽积为N的信号,该算法计算复杂度为O(N logN)。我们还讨论了离散分数傅里叶变换的定义。
引言
略……
预备知识
分数傅里叶变换
定义 { F f } ( x ) \{\mathcal{F}f\}(x) {Ff}(x)表示对 f ( x ) f(x) f(x)做一次傅里叶变换, { F a f } ( x ) \{\mathcal{F}^af\}(x) {Faf}(x)表示连续对 f ( x ) f(x) f(x)做 a a a次傅里叶变换。
根据傅里叶变换的定义,有 { F 2 f } ( x ) = f ( − x ) \{\mathcal{F}^2f\}(x)=f(-x) {F2f}(x)=f(−x)和 { F 4 f } ( x ) = f ( x ) \{\mathcal{F}^4f\}(x)=f(x) {F4f}(x)=f(x)(注:使用信号与系统里的傅里叶变换定义公式推导时可能会差 2 π 2\pi 2π倍,需要将 ω \omega ω换成 2 π f 2\pi f 2πf并以 f f f作为积分变量计算),可见傅里叶变换周期为 a = 4 a=4 a=4,于是设定 a a a的定义域为 0 < ∣ a ∣ < 2 0<|a|<2 0<∣a∣<2,负数时表示逆傅里叶变换。
将 a a a次傅里叶变换用卷积表示:
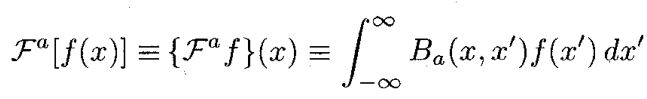
其中 ≡ \equiv ≡表示恒等于, B a ( x , x ′ ) B_a(x,x') Ba(x,x′)表示卷积核,注意 x ′ x' x′并不是表示 x x x的导数,只是一个新的变量,用于区分 x x x。
这个卷积核有前人推导过了,表达式如下:
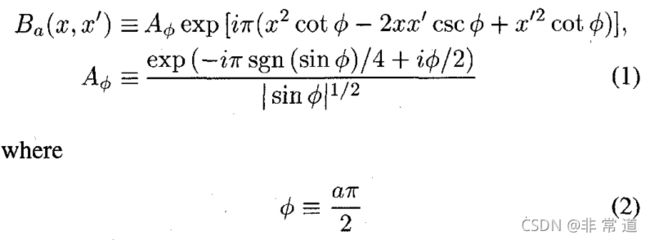
其中 i i i表示虚数单位。
当 a = 0 a=0 a=0时, B a ( x , x ′ ) = δ ( x − x ′ ) B_a(x,x')=\delta(x-x') Ba(x,x′)=δ(x−x′), δ \delta δ表示冲激函数,显然,根据冲激函数定义,当且仅当 x ′ = x x'=x x′=x时,积分有非零值,因此 { F 0 f } ( x ) = f ( x ) \{\mathcal{F}^0f\}(x)=f(x) {F0f}(x)=f(x).
当 a = ± 2 a=\pm2 a=±2时, B a ( x , x ′ ) = δ ( x + x ′ ) B_a(x,x')=\delta(x+x') Ba(x,x′)=δ(x+x′),同理,此时 { F ± 2 f } ( x ) = f ( − x ) \{\mathcal{F}^{\pm2}f\}(x)=f(-x) {F±2f}(x)=f(−x).
当 a = 1 a=1 a=1时, A ϕ = 1 A_\phi=1 Aϕ=1, B a ( x , x ′ ) = e − 2 π i x x ′ B_a(x,x')=e^{-2\pi i x x'} Ba(x,x′)=e−2πixx′,卷积核为傅里叶变换核, { F 1 f } ( x ) = F ( x ) \{\mathcal{F}^1f\}(x)=\mathcal{F}(x) {F1f}(x)=F(x)
当 a = − 1 a=-1 a=−1时, A ϕ = 1 A_\phi=1 Aϕ=1, B a ( x , x ′ ) = e 2 π i x x ′ B_a(x,x')=e^{2\pi i x x'} Ba(x,x′)=e2πixx′,卷积核为逆傅里叶变换核, { F − 1 f } ( x ) = F − 1 ( x ) \{\mathcal{F}^{-1}f\}(x)=\mathcal{F}^{-1}(x) {F−1f}(x)=F−1(x)
傅里叶变换对如下:
F ( x ) = F ( f ( x ′ ) ) = ∫ − ∞ + ∞ f ( x ′ ) e − 2 π i x x ′ d x ′ F(x)=\mathcal{F}(f(x'))=\int_{-\infty}^{+\infty}f(x')e^{-2\pi ixx'}dx' F(x)=F(f(x′))=∫−∞+∞f(x′)e−2πixx′dx′
f ( x ′ ) = F − 1 ( F ( x ) ) = ∫ − ∞ + ∞ F ( x ) e 2 π i x x ′ d x f(x')=\mathcal{F}^{-1}(F(x))=\int_{-\infty}^{+\infty}F(x)e^{2\pi ixx'}dx f(x′)=F−1(F(x))=∫−∞+∞F(x)e2πixx′dx
(与平常课本上学的在形式上不太一样,不过物理意义是相同的,只不过是把角频率换成了频率)
可以证明有如下性质成立:
F a 1 F a 2 = F a 1 + a 2 \mathcal{F}^{a_1}\mathcal{F}^{a_2}=\mathcal{F}^{a_1+a_2} Fa1Fa2=Fa1+a2
傅里叶变换的核函数,其完备集合是Hermite-Gaussian 函数:

(这块不细讲了)
为方便起见, { F a f } ( x ) \{\mathcal{F}^{a}f\}(x) {Faf}(x)简写为 f a ( x ) f_a(x) fa(x)
和维纳分布的关系以及分数阶傅里叶域的概念
如果时域函数为 f ( x ) f(x) f(x),则维纳分布函数为:
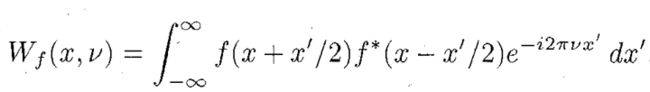
粗略来讲,维纳分布函数给出了信号在时域和频域上的能量分布,有如下特点:
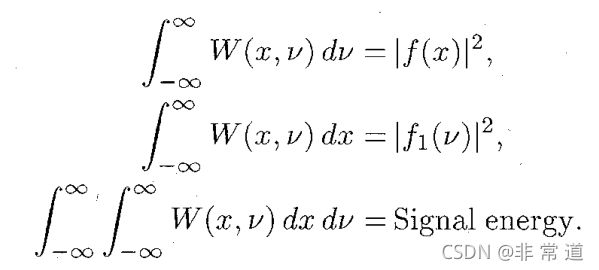
分数阶傅里叶变化的出现,丰富了时域和频域的概念,以时域中的时间为x轴,频域中的频率为y轴,可以画出时频域平面,即分数傅里叶域。维纳分布函数也可以通过几何的方法,改写为:
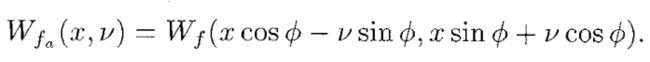
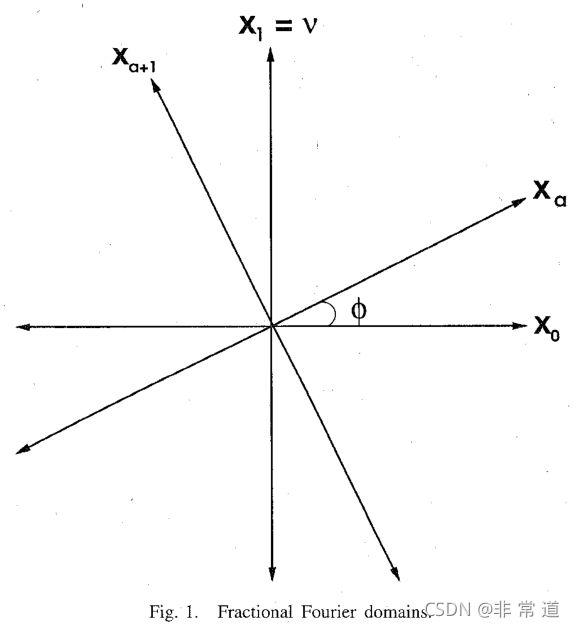
分数阶傅里叶变换突破了时域和频域的概念,可以做到任意角度的变换。
时域、频域和维格纳空间中的紧凑型
略……
离散傅里叶变换
计算连续分数阶傅里叶变换的方法
上述计算连续分数阶傅里叶变换的公式,很难用解析的方法求解,因此我们通常使用数值计算方法,比如用指数或者二次函数近似,但是这样通常情况下需要大量的样本。当 a a a接近 0 0 0和 ± 2 \pm2 ±2时,情况更加严重。
有一种快速计算方法是利用 F a = F 1 F a − 1 \mathcal{F}^a=\mathcal{F}^1\mathcal{F}^{a-1} Fa=F1Fa−1,其中 F a − 1 \mathcal{F}^a-1 Fa−1可以直接得到。
还有一种方法用到了核函数的频谱分解。
尽管这两种方法都期望能得到正确的结果,但是我们不会进一步考虑他们,因为他们的计算复杂度为 O ( N 2 ) O(N^2) O(N2)
分数阶傅里叶变换的快速算法
分数阶傅里叶变换是一类更普遍的变换,通常被称为linear canonical transformations 或 quadratic-phase transforms。这些变换通常能分解成一系列简单的操作,比如线性调频卷积、线性调频相乘、缩放和原始傅里叶变换。这里我们主要研究两种分解方法,对应两种独特的方法。
方法一
首先,我们将分数阶傅里叶变换分解成一个线性调频相乘跟着一个线性调频卷积跟着另一个线性调频相乘。在这个方法中,假设 a ∈ [ − 1 , 1 ] a\in [-1,1] a∈[−1,1],可以将分数阶傅里叶变换公式变为:


这里 g ( x ) g(x) g(x)和 g ′ ( x ) g'(x) g′(x)代表中间结果,其中 ′ ' ′不表示导数, β = csc ϕ \beta=\csc\phi β=cscϕ。
在第一步(公式16)中,我们把 f ( x ) f(x) f(x)乘以了一个线性调频函数,首先我们要获得 g ( x ) g(x) g(x)的采样,需要内插。接下来是把 g ( x ) g(x) g(x)卷积上一个线性调频函数。注意到 g ( x ) g(x) g(x)带宽有限,因此线性调频函数可以等价为一个带宽有限函数:
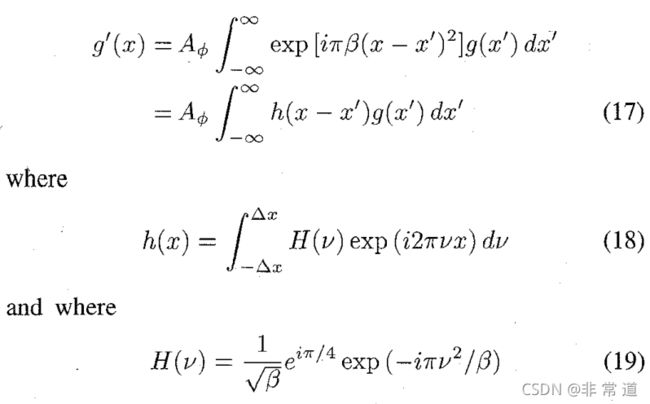
注意到式(19)是线性调频函数 exp ( i π β x 2 ) \exp(i\pi \beta x^2) exp(iπβx2)的傅里叶变换。 h ( x ) h(x) h(x)可以认为是菲涅尔积分:
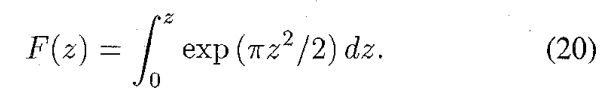
g ′ ( x ) g'(x) g′(x)被采样后,结果为:
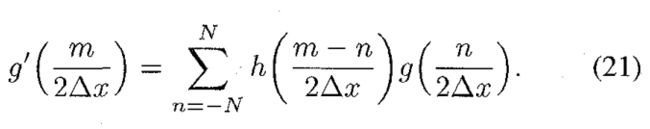
这个卷积可以通过快速傅里叶变换计算。
目前采样间隔为 1 / 2 Δ x 1/2\Delta x 1/2Δx,需要使用抽删操作,大批删减样本,使样本间隔变为 1 / Δ x 1/\Delta x 1/Δx。
总而言之, f ( x ) f(x) f(x)和 f a ( x ) f_a(x) fa(x)都是以 1 / Δ x 1/\Delta x 1/Δx为间隔采样的,均为 N N N个样本,,将这些样本以列向量表示,分别为 f \mathbf{f} f和 f a \mathbf{f}_a fa,则总程序可以表示为:
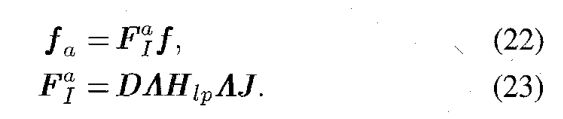
D \mathbf{D} D和 J \mathbf{J} J表示抽删和内插操作的矩阵, Λ \mathbf{\Lambda} Λ表示线性调频相乘, H l p \mathbf{H}_{lp} Hlp对应卷积操作。
如果我们只关心计算和绘制给定的连续函数 f ( x ) f(x) f(x)的分数阶傅里叶变换,那么抽删和内插操作可以省去。
注意 a a a的定义域是 − [ 1 , 1 ] -[1,1] −[1,1],如果 a a a在区域之外,可以利用分数阶傅里叶变化的对称和周期性将 a a a转换到定义域内。
方法二
接下来我们关注一个改进的方法,这个方法不需要菲涅尔积分。分数阶傅里叶变换公式可以写为:
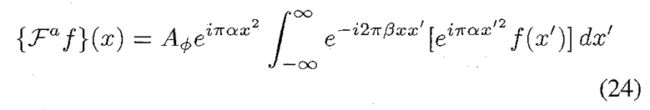
其中 α = cot ϕ , β = csc ϕ \alpha=\cot\phi,\beta=\csc\phi α=cotϕ,β=cscϕ
在一堆看不懂的假设后, e i π α x ′ 2 f ( x ′ ) e^{i\pi\alpha x'^{2}}f(x') eiπαx′2f(x′)可以用香农内插公式书写:
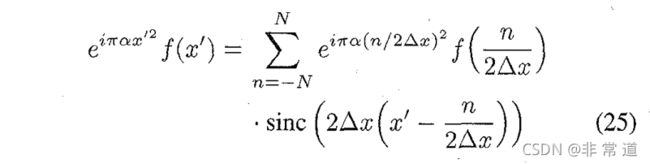
其中 N = ( Δ x ) 2 N=(\Delta x)^2 N=(Δx)2,改变求和顺序后可以得到:

里面的积分等于
![]()
窗函数可以去掉,公式写为
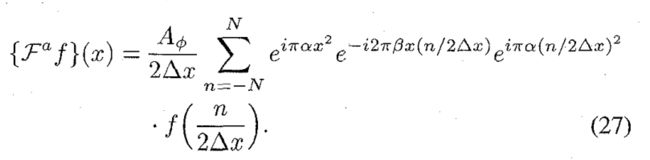
采样后的变换函数可以写为:
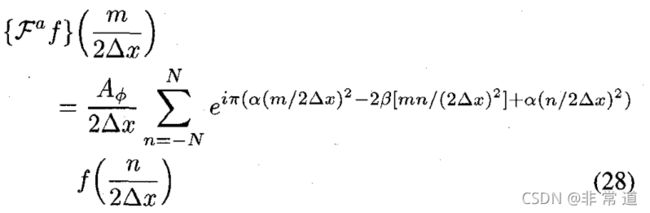
这是一个有限的求和,允许我们依照原函数的采样求得分数傅里叶变换的采样。直接计算需要 O ( N 2 ) O(N^2) O(N2)次乘法,但是接下来我们介绍如何用 O ( N log N ) O(N\log N) O(NlogN)的时间复杂度计算。把上式通过代数变换变为:
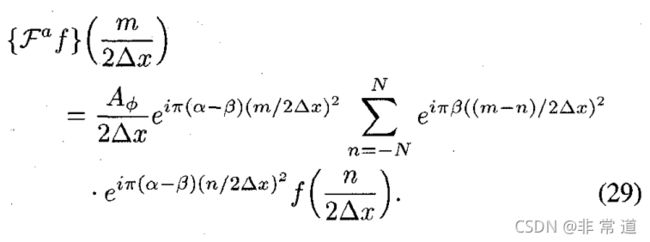
可以很明显的看到,求和符号里面是关于 e i π β ( n / 2 Δ x ) e^i\pi\beta(n/2\Delta x) eiπβ(n/2Δx)和线性调频调制后的 f ( x ) f(x) f(x)线性卷积。线性卷积可以使用快速傅里叶变换(fft)计算得到,而fft的计算复杂度为 O ( N log N ) O(N\log N) O(NlogN)。
得出的结果样本在乘以一个线性调频函数,就是最终结果。
计算过程用矩阵和向量总结如下:
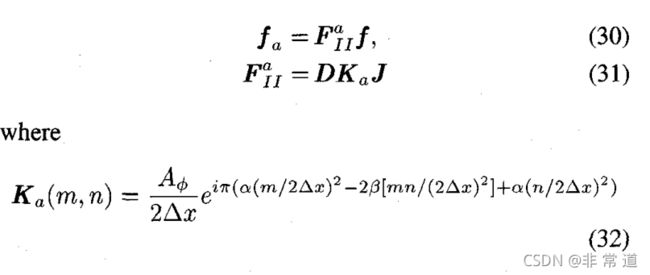
注意 ∣ m ∣ , ∣ n ∣ < N |m|,|n|
在这个方法中假设了 0.5 ≤ ∣ a ∣ ≤ 1.5 0.5\leq|a|\leq1.5 0.5≤∣a∣≤1.5,不过我们可以使用分数傅里叶变换的可加性将其拓展到任意定义域,比如对于范围 0 ≤ ∣ a ∣ ≤ 0.5 0\leq|a|\leq0.5 0≤∣a∣≤0.5,可以使用以下变换式:
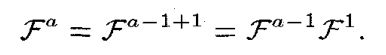
注意最后一项不是表示乘积,是表示连续做两次变换。
在这种计算方法中,分数阶傅里叶变换和原傅里叶变换之间的关系为:
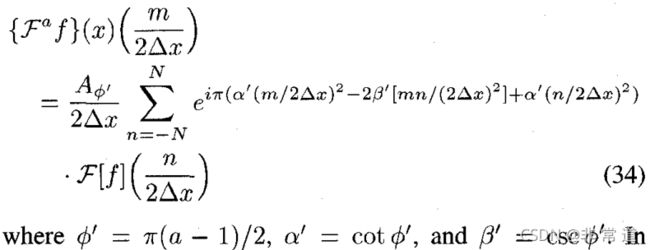
可以看出
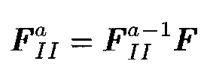
其中 F \mathbf{F} F表示原傅里叶变换矩阵.
代码与注释
论文的原理部分翻译到此结束了,下面是按照原论文的思想,参考了其它博主的代码实现,加了一些注释便于理解。
function Faf = myfrft(f, a)
%分数阶傅里叶变换函数
%输入参数f为原始信号,a为阶数
%输出结果为原始信号的a阶傅里叶变换
N = length(f);%总采样点数
shft = rem((0:N-1)+fix(N/2),N)+1;%此项等同于fftshift(1:N),起到翻转坐标轴的作用
sN = sqrt(N);%看原文中对离散傅里叶变换的定义,有这个乘积项
a = mod(a,4);%按周期性将a定义在[0,4]
%特殊情况直接处理
if (a==0), Faf = f; return; end%自身
if (a==2), Faf = flipud(f); return; end%f(-x)
if (a==1), Faf(shft,1) = fft(f(shft))/sN; return; end%f的傅里叶变换
if (a==3), Faf(shft,1) = ifft(f(shft))*sN; return; end%f的逆傅里叶变换
%利用叠加性将阶数变换到0.5 < a < 1.5
if (a>2.0), a = a-2; f = flipud(f); end%a=2是反转
if (a>1.5), a = a-1; f(shft,1) = fft(f(shft))/sN; end%a=1是傅里叶变换
if (a<0.5), a = a+1; f(shft,1) = ifft(f(shft))*sN; end%a=-1是逆傅里叶变换
%开始正式的变换
alpha = a*pi/2;
tana2 = tan(alpha/2);
sina = sin(alpha);
f = [zeros(N-1,1) ; interp(f) ; zeros(N-1,1)];%使用香农插值,拓展为4N
% 以下操作对应原论文中公式(29)
% 线性调频预调制
chrp = exp(-1i*pi/N*tana2/4*(-2*N+2:2*N-2)'.^2);
f = chrp.*f;
% 线性调频卷积
c = pi/N/sina/4;
Faf = fconv(exp(1i*c*(-(4*N-4):4*N-4)'.^2),f);
Faf = Faf(4*N-3:8*N-7)*sqrt(c/pi);
% 线性调频后调制
Faf = chrp.*Faf;
% 乘以最前面的A_Phi项
Faf = exp(-1i*(1-a)*pi/4)*Faf(N:2:end-N+1);
end
function xint=interp(x)%香农插值
% sinc interpolation
N = length(x);
y = zeros(2*N-1,1);
y(1:2:2*N-1) = x;
xint = fconv(y(1:2*N-1), sinc([-(2*N-3):(2*N-3)]'/2));%计算卷积
xint = xint(2*N-2:end-2*N+3);
end
function z = fconv(x,y)%利用fft快速计算卷积
N = length([x(:);y(:)])-1;%计算最大点数
P = 2^nextpow2(N);%补零
z = ifft( fft(x,P) .* fft(y,P));%频域相乘,时域卷积
z = z(1:N);%去零
end
测试
使用如下代码进行测试:
close all
a=0:0.25:4;%分数阶傅里叶变换阶数
%生成一个窗函数
fx=zeros(500,1);
fx(150:250)=1;
for ai=a
figure
F=myfrft(fx,ai);
plot(abs(F))
title("a="+num2str(ai))
grid on
ylim([0,5])
end
首先生成一个窗函数,长度为500,在150到250点处为1,其余为0。
学过信号与系统的同学都知道,窗函数的傅里叶变换是一个Sa函数(也称Sinc函数),选取傅里叶变换的阶数为0到4之间,间隔为0.25,观察每一个结果。我将分数阶傅里叶变换的结果做成了一个动图,可以更加直观的理解分数阶傅里叶变换的物理意义和时频域的概念。