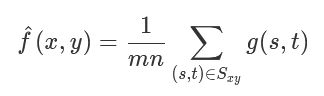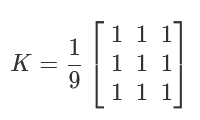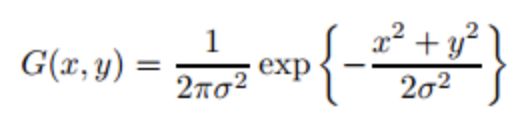Python OpenCV5：OpenCV 图像平滑

1. 图像噪声

图像的采集、处理、传输等过程难免会受到噪声的污染，阻碍了人们对图像的理解和分析。

1.1 椒盐噪声

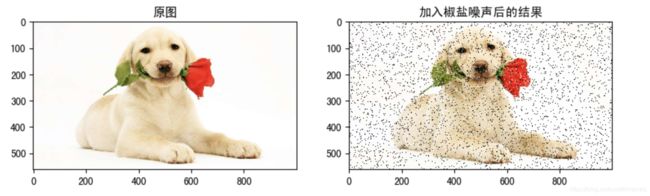
椒盐噪声也称为脉冲噪声，是图像中经常看到的一种噪声。 它是一种随机出现的白点或黑点。 它可能是亮区中的黑色像素或暗区中的白色像素，或两者兼有。 椒盐噪声可能是由图像信号的突然强干扰、模数转换器或比特传输错误引起的。 例如，传感器故障导致像素值为最小值，传感器饱和导致像素值为最大值。

1.2 高斯噪声

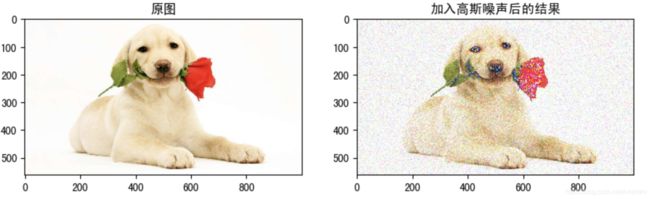
高斯噪声也称为正态噪声，指噪声密度函数服从高斯分布的一类噪声。 由于高斯噪声在空间和频域中的数学上的简易性，在实践中经常使用这种噪声模型。 高斯随机变量 z 的概率密度函数由下式给出：

 

其中，z代表灰度值，μ代表z的平均值或期望值，σ代表z的标准差。 标准差的平方 σ^2 称为z的方差。

2. 图像平滑方法

从信号处理的角度来看，图像平滑就是去除高频信息，保留低频信息。 所以我们可以对图像进行低通滤波。 低通滤波可以去除图像中的噪声，使图像平滑。

根据滤波器的不同，图像平滑方法可分为均值滤波、高斯滤波、中值滤波等。

2.1 均值滤波

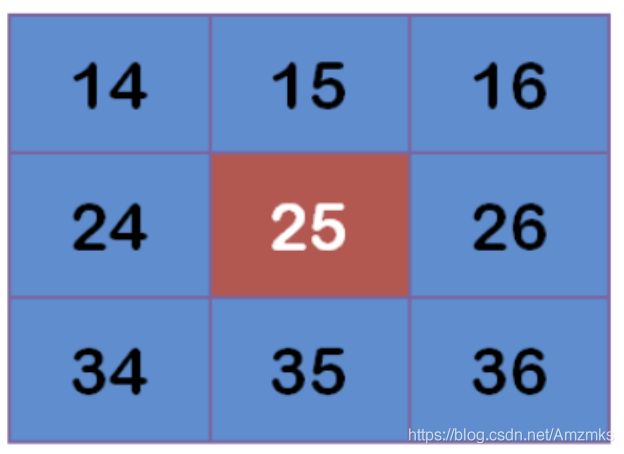
均值滤波模板用于滤除图像噪声。 令 S xy 表示中心在 (x, y) 且大小为 m×n 的矩形子图像窗口的坐标组。

均值滤波可以表示为：

均值滤波由归一化卷积框完成，它将中心元素替换为卷积框覆盖区域内所有像素的平均值。 例如，这是一个 3x3 的标准化均值滤波器：

cv.blur(src, ksize, anchor, borderType)

参数：

src 输入图像

ksize 卷积核的大小

anchor 核中心，默认值(-1,-1)

borderType 边界类型

均值滤波的优点：算法简单，计算速度较快。

均值滤波的缺点：去噪的同时去除了很多细节，图像变得模糊。

2.2 高斯滤波

二维高斯是构建高斯滤波器的基础，其概率分布函数如下：

G(x,y) 的分布是凸出的帽子的形状。这里σ可以看成两个值，一个是x方向的标准差σx，另一个是y方向的标准差σy。

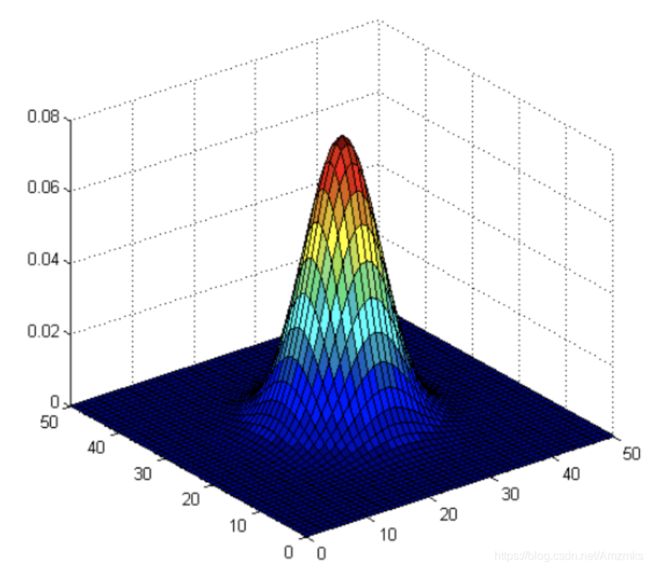
当σx和σy的值较大时，整个形状趋于平坦； 当σx和σy的值较小时，整个形状变得更加突出。正态分布是一条钟形曲线， 离中心越近，数值越大；离中心越远，数值越小。计算平滑结果时，只需要以中心点为原点，根据其他点在正态曲线上的位置，为其分配权重，即可得到加权平均值。

高斯平滑对于从图像中去除高斯噪声非常有效。

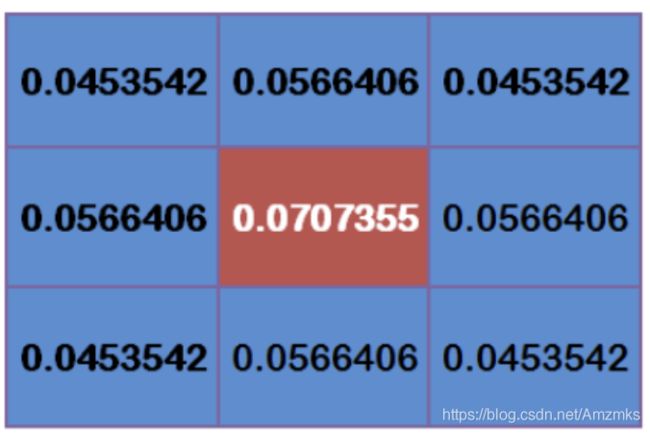
高斯平滑首先需要确定权重矩阵。假设中心点的坐标为(0,0)，那么最近的8个点的坐标如下：

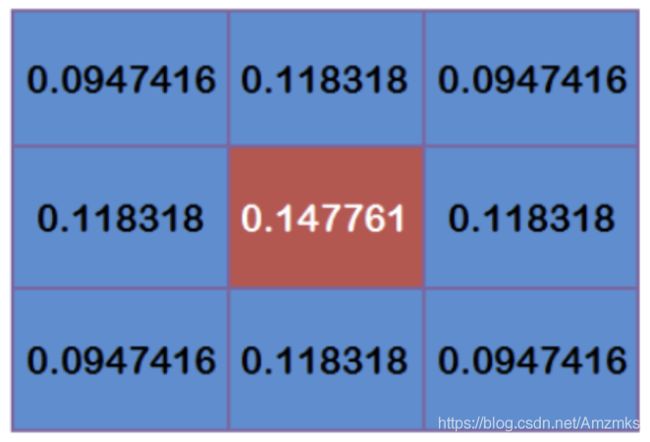
其他更远的点可以类推。计算权重矩阵还需要设置σ的值。 假设σ=1.5，模糊半径为1的权重矩阵如下：

这 9 个点的权重之和等于 0.4787147。如果只计算这9个点的加权平均值，它们的权重之和必须等于1。因此，必须将上述9个值除以0.4787147才能得到最终的权重矩阵。 

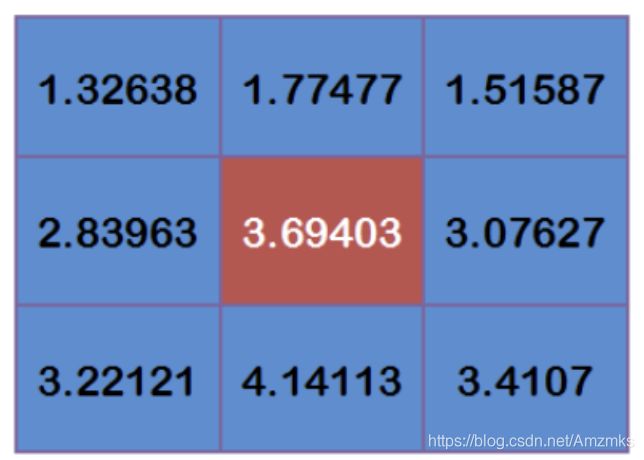
通过权重矩阵，可以计算出高斯模糊的值。 假设有9个像素，灰度值（0~255）如下： 

每个点乘以相应的权重值：

可得出：

将这 9 个值相加就是中心点处的高斯模糊值。 对所有点重复这个过程，得到高斯模糊图像。 如果原始图像是彩色图像，可以分别对R、G、B三个通道进行高斯平滑。

cv.GaussianBlur(src,ksize,sigmaX,sigmay,borderType)

参数：

src 输入图像

ksize 高斯卷积核的大小，卷积核的宽度和高度都应为奇数，且可以不同

sigmaX 水平方向的标准差

sigmaY 竖直方向的标准差，默认为0，表示与sigmaX相同

borderType 填充边界类型，默认为BORDER_DEFAULT

2.3 中值滤波

中值滤波是一种典型的非线性滤波技术。 其基本思想是用像素邻域的灰度值的中值代替像素的灰度值。

中值滤波对于椒盐噪声特别有用，因为它不依赖于与典型值非常不同的邻域值。

cv.medianBlur(src, ksize)

参数：

src 输入图像

ksize 卷积核的大小

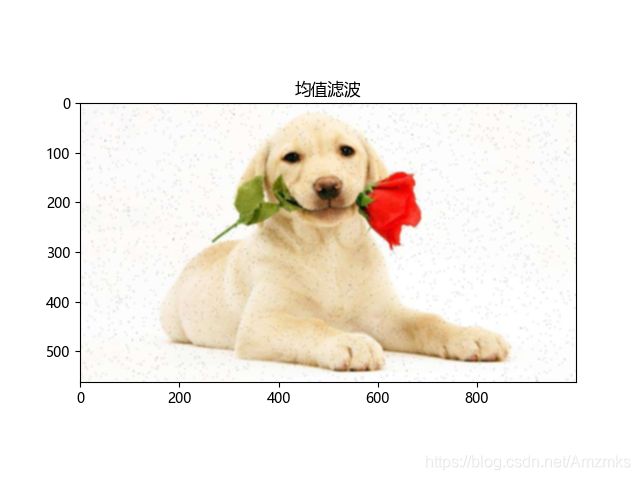
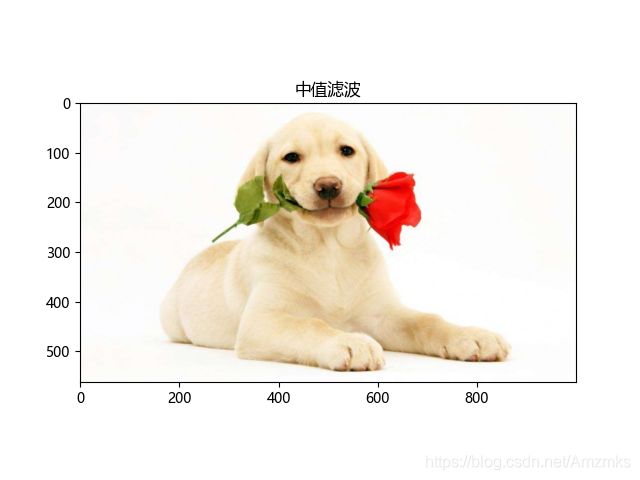
例：对图1进行均值滤波和中值滤波去除噪声，对图2进行高斯滤波去除噪声。

图1：有椒盐噪声的图像。

图2：有高斯噪声的图像。

import cv2 as cv
import matplotlib.pyplot as plt
import matplotlib

font = {
    "family": "Microsoft YaHei"
}
matplotlib.rc("font", **font)

dogsp = cv.imread("./image/dogsp.jpeg")
doggau = cv.imread("./image/dogGauss.jpeg")

# 均值滤波
dog = cv.blur(dogsp, (5, 5))
plt.imshow(dog[:, :, ::-1])
plt.title("均值滤波")
plt.show()

# 高斯滤波
dog = cv.GaussianBlur(doggau, (3, 3), 1)
plt.imshow(dog[:, :, ::-1])
plt.title("高斯滤波")
plt.show()

# 中值滤波
dog = cv.medianBlur(dogsp, 3)
plt.imshow(dog[:, :, ::-1])
plt.title("中值滤波")
plt.show()

输出：