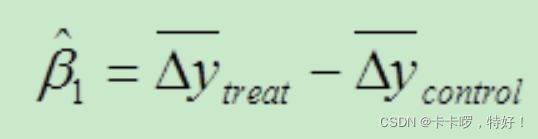跨时横截面的混合:简单面板数据方法
1. 独立混合横截面数据
在不同时点从一个大总体中随机抽样得到的随机样本。当其他条件都保持不变时,由于该数据都是由独立抽取的观测所构成,不同观测误差项的相关性被排除。但在不同时点上抽样可能导致样本性质与时间相关,使其不再保持单独随机样本中同分布的性质(例如:时点1的与时点2存在系统性差异。)。
2. 使用独立混合横截面的理由
(1)增大样本容量(应保证解释变量与被解释变量与时间无关)
(2)反映不同年份影响效果的差异。(分布差异由虚拟变量解决;政策评估)
3. 对跨时结构性变化的邹至庄检验
(1)用邹至庄检验来检验多元回归函数在两个时期之间是否存在差别。
(2)对多时期计算邹至庄检验统计量的办法
4. 利用混合横截面作政策分析
(1)自然实验与真实实验
自然实验(准实验)是指某些外生事件改变了观测样本运行的环境。一个自然实验总有一个不受政策变化影响的对照组和一个受外生事件影响的处理组。自然实验中,政策发生后才能确定处理组和对照组。在真实实验中,处理组和对照组是随机而明确地抽取的。
为了控制对照组和处理组之间的系统差异,可以按照使用目的将样本分为4组:变化前的对照组、变化后的对照组、变化前的处理组和变化后的处理组。对照组称为C,处理组称为T,并设置虚拟变量dT,如果样本属于处理组,则dT=1,否则等于0。令d2为第2个时期的虚拟变量,模型方程为y=β0+δ0d2+β1dT+δ1d2·dT+其他因素。其中,y是结果变量;δ1度量政策效应。当回归中没有其他因素时,δ∧1是倍差估计量,满足:δ∧1=(y_2,T-y_2,C)-(y_1,T-y_1,C)。
(2)政策的平均处理效应及其估计方法
平均处理效应度量的是对y的平均结果的“处理”或政策效应。估计值为:δ∧1=(y_2,T-y_1,T)-(y_2,C-y_1,C),该值与进行差分的方式无关。估计方法主要有:
①计算每个时期处理组和控制组的平均值之差,再对不同时期的上述差值做差分。
②分别计算处理组和控制组不同时期的平均值变化,再对上述差值做差分。
5. 两期面板数据分析
(1)面板数据的定义
区别于独立混合横截面,面板数据是指在不同时间跟踪同一批个体,确保每个样本个体在不同时间都有观测值,其兼具横截面和时间序列的特征。如果每个个体进入观测的时间跨度都一致,则称为平衡面板,否则称为非平衡面板。(思考:分辨非平衡面板与独立混合横截面数据)
(2)固定效应模型
令i表示横截面单位,t表示时期,可将含有单个可观测解释变量的模型写成:yit=β0+δ0d2t+β1xit+ai+uit,t=1,2。其中,变量d2t是一个在t=1时取值为零而在t=2时取值为1的虚拟变量,它不随i而变化;误差uit通常被称为特异误差或时变误差,包含影响yit且随时间变化的所有无法观测的因素;变量ai包含影响yit但又不随时间而变化的所有无法观测的因素,一般都被称为非观测效应、固定效应或非观测异质性。因此,上述模型被称为非观测效应模型或固定效应模型(注意:d2t与ai的设定,前者因时而变,后者因个体而不同)。
(3)估计β1的一种方法
在两时期面板数据中估计参数β1的一种方法是:混合两时期的数据进行OLS估计。将模型写成:yit=β0+δ0d2t+β1xit+vit,t=1,2。其中,vit=ai+uit常被称为复合误差。即使假定特异误差uit与xit无关,如果ai与xit相关,混合OLS估计就是偏误且不一致的。为了得到一致的估计量,必须假定非观测效应ai与xit无关。此类由于遗漏某些不随时间而变化的变量导致的偏误,有时被称为异质性偏误。
(4)一阶差分方程
在面板数据的大多数应用中,非观测效应ai与解释变量都是相关的。考虑到个体的ai不随时间变化,通过取两时期数据的差分可以解决上述问题。
对横截面的第i个观测值,把两年的方程分别写为:yi2=(β0+δ0)+β1xi2+ai+ui2(t=2),yi1=β0+β1xi1+ai+ui1(t=1)。两个方程相减可得:yi2-yi1=δ0+β1(xi2-xi1)+(ui2-ui1),简化为:∆yi=δ0+β1∆xi+∆ui。该式称为一阶差分方程,它是由单个横截面方程对每个变量都取时间上的差分所得到的。如果容许xit与不随时间而变化的无法观测因素相关,且∆ui与∆xi无关,这就是在一阶差分方程中的严格外生性假定。此时对β1进行OLS估计,得到β1的OLS估计量为一阶差分估计量。另一个关键条件是,∆xi必须因i的不同而有所变化。要用通常的OLS得到精确的无偏估计,还需要满足同方差性。
6. 用面板数据作政策分析
(1)两期面板数据
面板数据被广泛应用于政策分析,特别是项目评估。在第一个时期先得到一个观测样本,然后让一部分横截面单位参与下一个时期举办的某个项目,剩余的单位则作为对照组。可以通过一阶差分估计量评估政策效果。
在项目评估模型中,令yit为结果变量,progit为项目参与虚拟变量。最简单的非观测效应模型为:yit=β0+δ0d2t+β1progit+ai+uit。
(1)如果项目参与仅发生在第二个时期,则β1的OLS估计量为:
有了面板数据,便可以对同样的横截面单位取y在不同时期的差分,从而控制个人、企业或城市特有的效应
(2)如果项目参与发生在两个时期。β∧1代表着控制随时间而变化之后,因项目参加所致的Y的均值的变化。这样就可以控制那些可能与项目相关且随着时间而变化的变量。
(2)多于两期的差分法
扩展到多期的固定效应模型为:yit=δ1+δ2d2t+δ3d3t+β1xit1+…+βkxitk+ai+uit。
关键假定是特异误差与每一时期的解释变量都无关:Cov(xitj,uis)=0,∀t,s和j。即把非观测效应ai去掉后,解释变量都是严格外生的。该假定排除了当期特异误差uis影响未来几期解释变量的可能性;但当xitj是滞后因变量时,这种情形则必定发生。如果遗漏了一个重要的随时间而变化的变量,则上式一般是不成立的。一个或多个解释变量存在测量误差时,也会使上式成为谬误。
如果非观测效应ai与任一解释变量相关,则xitj将与复合误差vit=ai+uit相关,使用混合OLS将导致有偏误而又不一致的估计值。可以取相邻期的差分把ai去掉,得到:∆yit=δ2∆d2t+δ3∆d3t+β1∆xit1+…+βk∆xitk+∆uit。如果该方程满足经典线性模型假定,则混合OLS将得到无偏估计量,并且t和F统计量是有效的,且系数具有一致性。
多于两期的数据,要使通常的标准误和检验统计量确当,必须假定∆uit是序列无关的。若uit遵循一个稳定的AR(1)模型,则uit是序列相关的;只有当uit遵循随机游走时,∆uit才是序列无关的。
(3)一阶差分方程中的序列相关检验
令rit=∆uit表示原始误差的一阶差分。若rit遵循AR(1)模型:rit=ρri,t-1+eit,通过混合OLS估计差分方程并求出残差r∧it,然后将r∧it对r∧i,t-1(t=3,…,T;i=1,…,n)进行混合OLS回归,并计算r∧i,t-1系数的标准t检验(或异方差-稳健的t统计量)。ri,t-1的系数ρ∧就是ρ的一致估计量。
当误差中没有序列相关时,通常处理异方差性的方法都是适用的,既可以使用布罗施-帕甘和怀特异方差检验,又可以计算稳健标准误。
(4)一阶差分面板数据的潜在缺陷
(1)当关键解释变量在不同时期变化不大或不随时间而变化,差分的效果不明显。
(2)虽然xitj有足够的时间变异,但由于差分后带来自相关性,一阶差分(FD)估计仍可能存在严重偏误。
(3)回归元必须满足严格外生性假定。若假定不满足,则更多的时期通常仍不能消除FD估计量的不一致性。
(4)若一个或多个解释变量存在测量误差,尤其是在经典变量误差模型中,差分估计可能比混合OLS估计更糟。对一个测量糟糕的回归元进行差分,相对其与差分误差(因经典测量误差所致)之间的相关,降低了变异,从而导致潜在相当大的偏误。