机器学习笔记(菜鸟版

机器学习笔记

（之前已经写过一些基本的概念了，这里就不过多的赘叙了）

监督学习

这一类是用于分类问题上面的
监督学习就是每个数据集都会提供一份答案
而无监督学习则是没有答案，需要机器自己进行一个分类
也就是进行聚类
或者是通过哦相似度量来进行一个分类

而两者的最大区别在于
到底有没有答案或者是衡量的标准
所以也就导致了 有无答案集成为选择两者的一个最大因素，除此之外还有就是两者是否会有标签

过拟合与欠拟合

通俗的理解如下：
当你做作业做了太多关于f（x）的题目
这也就导致了思维的固化
等到了考试的时候，面对g（x）的题目（但是本质还是f（x））就一脸懵b的状态
这就是过于拟合的状态，就是机器的方法过于贴近样本集反而可能会脱离本质？

欠拟合的意思就是作业做太少了，一上考场这没见过，那没见过

损失函数

所有的损失函数都是关于参数o/o1/o2…的函数
（这有点焦头烂额了）

1.较简单的，大多用于分类算法的损失函数，如果用于回归函数就过于苛刻了，这个条件

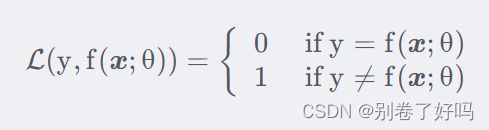
这里的函数指的是 每个参数对应全部的样本集进行比较，然后再相加
例如： 1,3,3,4,15
如果使用 y=x
则 f(o=1)=(1=1)+(3!=2)+…
=0+1+0+0+1=2
说明只有两个数据不拟合
如果使用y=3x
则 f(o=1)=(3!=1)+(6!=2)+…
=1+1+1+1+0=4
说明只有一个数据拟合
这个时候我们就可以画出函数图

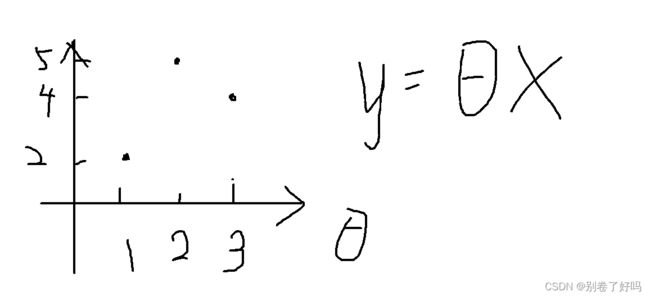
由此我们可以看到
当o=1的时候，损失函数值最小
也就是说损失的最小，拟合的最佳

1.最小二乘法，这个是回归函数使用的最多的

注释： m个样本集求和 得出来的测试值

所以对应的参数o1，o2不一样，所对应的 j(t)也不一样

例子：
我们先假设一个简单的函数把y= ?x，只有一个参数 ？
所以，损失函数的图像对应的x轴为 ？ 而y轴对于的是损失函数的值

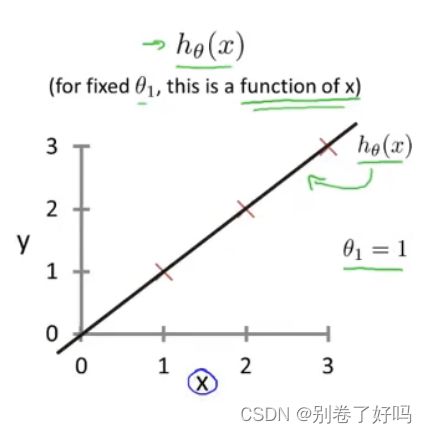
那么当 ？ =1 的时候，会发现全部数据都拟合了，所以得到以下的损失函数图像

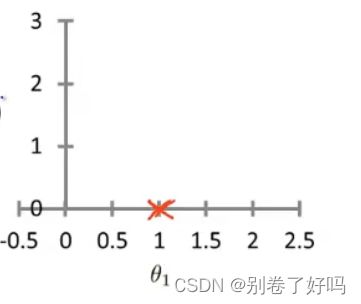
而当 ？ = 0.5，的时候会发现都不大拟合，所以损失函数会变大

计算过程如下：

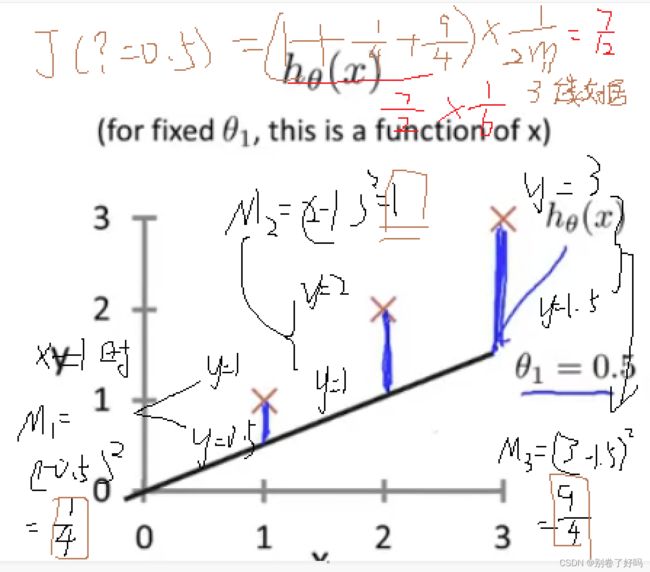
加上 ？ =1的时候的数据得到了

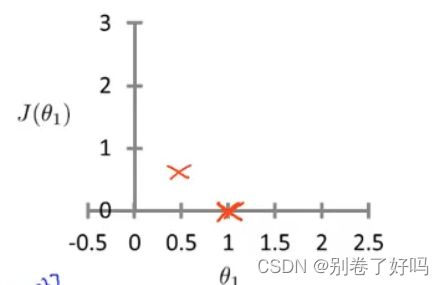
所以当有很多的数据的时候
就可以连城一条光滑的曲线

而最低点就是 损失最小的时候，这个就是后面的梯度下降法所要学习的

那么接下来就是开始变难了？不只是有一个参数

y= ax + b
所以，损失函数长这样

O0,O1 表示就是 j是关于O0,O1的函数，也就是 a,b
这个时候，损失函数就会变成一个三维的图像
x ----- a参数的数值
y ----- b参数的数值
z ----- 预测值的数值

计算的道理和上面是一样的
计算例子就算了（对手指，有点麻烦，呜呜呜）
大概长这样子

解释

比如： 假设 有数据集 ： 1,2,3
有答案集：2,3,5
我们使用了 y = x + 1该函数去拟合
就是 a = 1 ,b = 1

图有点丑

							(	1,		1,				1/6)

这个点表示的是 a=1,b=1时，损失函数对应的是1/6

梯度下降

emm挺好理解的，那我就说下计算方法吧

公式如下：

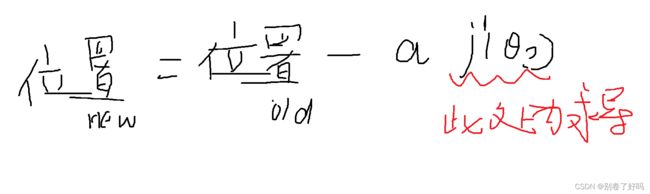
我们还是用简单的例子来讲解一下

同样的

所以，使用这种方法会向最低点靠近，当然也有可能会永远都到不了

而这个梯度下降法里面 a 这个参数代表的是每次下降的程度

如果a 过大，会导致函数发散，因为 j（x）求导会越来越大
并且，当有两个参数的时候，有可能只会到达局部的最优解，而不是全局的

最后（小声说

累了累了，还有 好多没学，这还是机器学习，后面1还有深度学习，呜呜呜
算法还不会，呜呜呜