KL/JS散度及Python实现
1. KL散度与JS散度的公式与代码的简要实现
import numpy as np
import scipy.stats as ss
np.random.seed(42)
# 随机生成;两个离散分布
X = [np.random.randint(2,11) for i in range(10)]
PX = X/np.sum(X) #X的概率分布
# print(X,PX )
Y = [np.random.randint(2,11) for i in range(10)]
PY = Y/np.sum(Y) #Y的概率分布
# print(Y,PY)
# KL散度:数学公式
KL = 0
for i in range(10):
KL += PX[i] * np.log(PX[i]/PY[i]) # print(KL)
def kld1(PX,QY):
return np.sum(PX*np.log(PX/QY))
# KL散度:scipy接口
def kld2(P,Q):
return ss.entropy(P,Q)
# JS散度:数学公式
def jsd1(P,Q):
M = (P+Q)/2
return 0.5*np.sum(P*np.log(P/M))+ 0.5*np.sum(Q*np.log(Q/M))
# JS散度:scipy接口提供
def jsd2(P,Q):
M = (P+Q)/2
return 0.5*ss.entropy(P,M)+ 0.5*ss.entropy(Q,M)
print('KL散度:',kld1(PX,PY),kld2(PX,PY))
print('KL散度不对称:',kld1(PY,PX) ,kld2(PY,PX))
print('KL散度的scipy接口:',kld2(X,Y))
print('JS散度:',jsd1(PX,PY),jsd2(PX,PY))
print('JS散度对称:',jsd1(PY,PX),jsd2(PY,PX))
2. python衡量数据分布的相似度/距离(KL/JS散度)
# python衡量数据分布的相似度/距离(KL/JS散度)
# KL散度:
'''
有时也称为相对熵,KL距离。对于两个概率分布P、Q,二者越相似,KL散度越小。
1.KL散度满足非负性
2.KL散度是不对称的,交换P、Q的位置将得到不同结果
'''
# Python实现:
import numpy as np
import scipy.stats
p = np.array([0.65,0.25,0.07,0.03])
q = np.array([0.6,0.25,0.1,0.05])
def KL_divergence(p,q):
return scipy.stats.entropy(p,q,base=2)
print(KL_divergence(p,q)) # 0.01693110139988926
print(KL_divergence(q,p)) # 0.019019266539324498
# JS散度:
'''
JS散度基于KL散度,同样是二者越相似,JS散度越小。
1.JS散度的取值范围在0-1之间,完全相同时为0
2.JS散度是对称的
'''
# Python实现:
import numpy as np
import scipy.stats as ss
p = np.array([0.65,0.25,0.07,0.03])
q = np.array([0.6,0.25,0.1,0.05])
q2 = np.array([0.1,0.2,0.3,0.4])
def JS_divergence(p,q):
M = (p+q)/2
return 0.5 * ss.entropy(p,M,base=2) + 0.5*ss.entropy(q,M,base=2)
print(JS_divergence(p,q)) # 0.004463665396105692
print(JS_divergence(p,q2)) # 0.35662209477833745
print(JS_divergence(p,p)) # 0.0
# 实例:身高分布预测比较
from scipy.stats import norm
import pandas as pd
import seaborn as sns
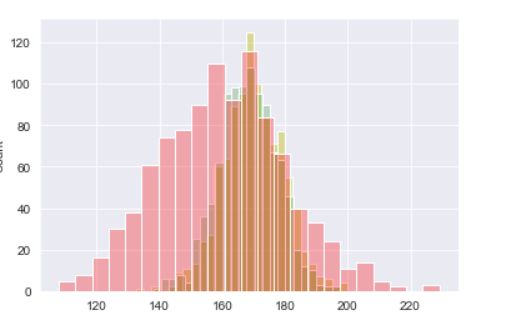
# 1000个均值170,标准差10的正太分布身高样本
h_real = norm.rvs(loc = 170,scale = 10,size = 1000)
h_predict1 = norm.rvs(loc = 168,scale = 9,size = 1000)
h_predict2 = norm.rvs(loc = 160,scale = 20,size = 1000)
def JS_div(arr1,arr2,num_bins):
max0 = max(np.max(arr1),np.max(arr2))
min0 = min(np.min(arr1),np.min(arr2))
bins = np.linspace(min0-1e-4,max0+1e-4,num = num_bins)
PDF1 = pd.cut(arr1,bins).value_counts()/len(arr1)
PDF2 = pd.cut(arr2,bins).value_counts()/len(arr2)
return JS_divergence(PDF1.values,PDF2.values)
print(JS_div(h_real,h_predict1,num_bins=20))
print(JS_div(h_real,h_predict2,num_bins=20))
附加:
# 忽略警告
import warnings
warnings.filterwarnings('ignore')
sns.set_style('darkgrid')
sns.histplot(h_real,color='y',alpha = 0.4)
sns.histplot(h_predict1,color='g',alpha = 0.2)
sns.histplot(h_predict2,color='r',alpha = 0.3)
# sns.distplot(h_real,color='y')
知识点:相比np.arange函数。两者最大差异是,linspace能够精确控制终止值终值,而arange能够更直接地控制序列中值之间的增量。
CK:
https://blog.csdn.net/blmoistawinde/article/details/84329103
https://blog.csdn.net/weixin_41896770/article/details/126997982