机器学习中隐马尔可夫模型（Hidden Markov Model, HMM）理论

隐马尔可夫模型（Hidden Markov Model, HMM）

前言 ：内容从实际案例到模型提取、建立、求解以及应用，侧重于该模型在机器学习中的研究和应用。

参考书：

《统计学习方法》

《The Model Thinker》

1. 马尔可夫宿命论

History is a cyclic poem written by time upon the memories of man. ------Percy Bysshe Shelley

1.1 案例

课堂注意力

假设课堂上学生听课有两种状态：集中和开小差。且学生集中和开小差之间转换概率是固定的，具体为：今天如果认真听讲，第二天仍认真听讲的概率为90%，开小差的概率为10%；如果今天开小差，第二天会认真听讲的概率为30%，仍旧开小差的概率为70%

如果转换概率不变，最终认真听讲和开小差人数会达到一个稳定状态。

推演整个变化过程如下（假设有100名同学）：

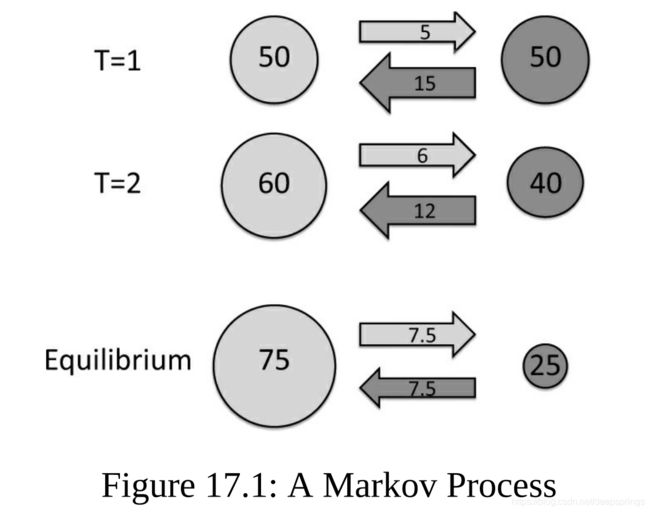
第一天：假设认真听讲和开小差人数各占一半（各50人）>>>>> [50, 50]

第二天：认真听讲的人中，5人（10%）变为开小差; 开小差的人中有15人认真听讲 >>>>> [60, 40]

此后，同第二天中推理一样，直到有一天，认真听讲的人有 75 人，开小差有 25 人，那么对于下一天认真听讲中，7.5（10%）变为开小差，开小差中，同样 7.5（10%）变为认真听讲。自此，认真听讲与开小差的人数达到固定（稳定状态）。

事实上，初始条件的改变、中途的干预也不会影响最终的结果，只要状态之间的转换概率不变。譬如通过课堂活动、增强监督来增加认真听讲的人数，但一旦这种干预停止，那么最终还是会回到 75 人认真，25 人开小差的境况。就像某种宿命。

情绪转变

对于一个人，假设情绪包含着三种状态：低落、平静、兴奋，且它们间转换的概率固定（由性格和环境确定），人最终会达到一个上述情绪状态占比稳定的状态。例如某人情绪达到稳定状态后低落占比较大，那么生活中的一次 party 所带来的全天兴奋是改变不了最终状态的，慢慢地人还是会回归到情绪低落之中。

精准扶贫

扶贫先扶智，就在于改变转换概率，而非直接发钱干预初始条件，因为这种干预对于改变最终状态没有用处。提高穷人技能、认知、态度才是要义。

纳什均衡与马尔可夫过程的异同

两者的最终结果都是达到平衡，回归到一种均衡态。但这两种均衡在原理和过程上有着本质上的区别。

纳什均衡见诸于博弈论中，是各方为了达到自己期望收益最大值而做出一系列努力和决策，最终达到了一种平衡态，而这种平衡态是一种不得不接受的结果，一旦有一方做出改变，那么只会让自身利益受损。譬如同类商铺总会扎堆出现。

马尔可夫过程，最终也是回归到一个均衡态，而这种均衡态是有一种宿命的味道。关键因素不加以改变，最终的结果始终如一，有着一种因果关系。

纳什均衡是各方博弈，且是非合作博弈，最终达到对峙妥协；马尔可夫过程则是系统根据自身特性，演变出的必然结果。

一些相关俗语

扶贫先扶智

江山易改，本性难移

授人以鱼不如授人以渔

1.2 宿命

一个系统如果满足如下条件

1. 系统中有有限多个状态
2. 状态之间切换的概率是固定的
3. 从任何一个状态出发都能找到一条路切换到任何一个其他状态
4. 系统中不能有单独几个状态形成闭环而把其他状态排斥在外

该系统就将陷入马尔可夫宿命当中，即无论外部做出多大努力，该系统都会最终演变到一个固定平衡态。

参考:

有趣视频

1. 【薛饿】冲出僵尸岛
2. 【看懂村】纳什均衡

2. 马尔可夫过程

以上从实际案例中引入了马尔克夫过程。

针对案例1中的系统马尔可夫过程可以用图示描述

将其抽象为一般数学模型：

对于一个随机过程 $q_1,q_2,\cdots ,q_N$，每个 $q_t$ 就是一个随机变量，每个随机变量在一个观测集合 $v=\{v_1,v_2,\cdots ,v_n\}$中取值，即 $q_t\in v$

在案例 1 中，随机过程 $ q_t$ 对应于某个学生的第 t 天的上课状态，观测集合 v 对应取值为 $\{认真，开小差\}$ 。

某一同学的具体随机过程可表示诸如：开小差，开小差，认真，认真，认真，认真……

根据马尔可夫过程特点，状态间存在转化，考虑第 t 与 t+1 过程

记从 $v_i$ 转移到状态 $v_j$ 概率为
$$P(q_{t+1}=v_j|q_t=v_i)=P_{ij}$$
使用转移矩阵
$$A=[P_{ij}{]}_{n\times n}$$
该矩阵包含了任意两个状态间的转化概率。转移矩阵性质：

$$\begin{gathered} 0\le P_{ij}\le 1 \\ \sum _{j=1}^n{P}_{ij}=1 \\ P(q_{t+1}=v_{t+1}|q_t=v_t,q_{t-1}=v_{t-1},\cdots ,q_0=v_0)=P(q_{t+1}=v_{t+1}|q_t=v_t) \end{gathered}$$

在案例 1 中，状态转移

	（到）认真	（到）开小差
（从）认真	90%	10%
（从）开小差	30%	70%

即转移矩阵
$$A_1=\left[\begin{array}{cc}90\%& 10\%\\ 30\%& 70\%\end{array}\right]$$

3. 隐马尔可夫模型

3.1 从 EM 算法

参考：EM 算法

复现三硬币模型

A, B, C 为三枚硬币，正面朝上的概率假设分别为 $\pi ,p,q$ ，进行投掷硬币实验：先投掷 A 硬币，结果用 x 表示，如果朝上(x=1)，投掷 B 硬币，否则(x=0)，投掷 C 硬币。最终结果记为 y，正面 y=1, 反面 y=0

假设经过 n 次实验，观测到结果 $y_1,y_2,\cdots ,y_n$

该模型是基于独立实验进行的，确切说是，每次是通过投掷 A 来选择决定后面操作，而每次投掷 A 硬币结果是独立同分布的（independentity identically distribution, iid），因此作出选择（选择投掷 B 或 C）的概率也是固定且无联系的。但现实中很多情况下，选择往往是相互联系的，即前一次的结果会对后一次结果产生影响。

假设去除掉 B 和 C 硬币投掷过程，将投掷 A 的结果显式提取出来，假设经过 10 次实验，考虑如下两种情况下的结果（选择B记为B，选择C记为C；为说明问题，数据比较极端）

	1	2	3	4	5	6	7	8	9	10
第一种情况	B	C	B	B	C	B	C	C	B	C
第二种情况	B	B	B	B	B	C	C	C	C	C

在之前 EM 算法视角下，这两种情况其实是等价的，因为两种情况下，都有 5 次选择了 B，5 次选择了 C，会得到相同的似然函数，因此参数估计也会是相同的。

但实际上，这两种情况下的结果明显是有差异的，第一种结果显示出一种随机性，而第二种结果像是有种惯性效果（i.e. 保持与前次结果相同的概率较大，变为另一种情况的概率小），之前对于第二种结果的解释和预测就会显现出局限性。而这就是隐马尔可夫要解决的问题。

在之前引入 EM 算法时，模型是通过隐藏层的选取（三硬币模型中的$\pi$，高斯混合模型中的${\alpha }_k$），以及观测层的观察（三硬币模型中的$p,q$，高斯模型中的$P(y_i|\theta )$）确定。

而类比之前，建立可解决问题的隐马尔可夫模型，需要隐藏层的选取（转移概率矩阵），需要观测层的观察（观测概率矩阵），因为模型具有时序性，需要给定一个初始值，才能生成后续值，因此还需要一个“导火索”，即 t=0 时刻下，取隐藏层第一值$q_i$的概率（初始状态概率向量）

3.2 从马尔可夫过程

对于上述三硬币模型，通过去除掉 B 和 C硬币投掷过程，显式展现了第一次投掷的结果，假设满足转移矩阵（参考上述第二种情况，使相同结果间相互转化概率较大），即显式展现了马尔可夫过程。

	到 B	到 C
从 B	90%	10%
从 C	10%	90%

但实际情况中，该过程是隐藏的，就类似于神经网络中的隐藏层，我们只能得到最终的投掷 B 或 C 后的结果，而选择 B 或 C 的这个过程是隐式进行的。

因此，对于一个包含马尔可夫过程，且该过程处于隐藏层的模型，就是隐马尔可夫模型。

3.3 到隐马尔可夫模型（HMM）

3.3.1 形式定义

名词

• 状态序列：隐藏的马尔可夫链随机生成的状态序列（对应于三硬币模型中，对B/C的选择；不可显式观测到）
• 观测序列：每个状态生成一个观测，由此产生的观测序列（对应于三硬币模型中，B/C投掷结果；最终能观测的结果）

隐藏层

设 $I$ 是长度为 T 的状态序列，Q 是所有可能状态的集合，
$$\begin{gathered} I=\{i_1,i_2,\cdots ,i_T\} \\ Q=\{q_1,q_2,\cdots ,q_N\} \end{gathered}$$

对于三硬币模型，隐藏层（选择B/C）随机过程（状态序列）为 $i_1,i_2,\cdots ,i_N$ ，也即对应于 B/C选择情况这一事件，对这一事件的结果在可能状态集合 Q 中取值，且 $Q=\{选择B，选择C\}$

假设第 1 个观测结果为 需要选择B投掷，该概率事件可记为 $P(i_1=B)$

该层为隐式进行，不可观察到。

观察层

设 O 是长度为 T 的观测序列，V 是所有可能的观测集合
$$\begin{gathered} O=\{o_1,o_2,\cdots ,o_T\} \\ V=\{v_1,v_2,\cdots ,v_M\} \end{gathered}$$

对于三硬币模型，观察层（投掷B/C）随机过程（观测序列）为 $o_1,o_2,\cdots ,o_T$ ，也即对应于最终能够观察到结果这一事件，对这一事件的观测结果在可能观测集合 V 中取值，且 $V=\{正面，反面\}$

假设第 1 个观测结果为 正面，该概率时间可记为 $P=(o_1=正面)$

3.3.2 模型建立

在 3.1 中说明了隐马尔可夫模型需要三个要素：

初始状态概率向量

记 t=1 时刻，模型从隐状态 $q_i$ 开始，而这一事件概率记为
$${\pi }_i=P(i_1=q_i)$$
且 $q_i\in Q$，对于所有情况，用一向量 $\pi$ 表示
$$\pi =({\pi }_i),i=1,2,\cdots ,N$$
状态转移概率矩阵

选定了初始状态 $q_i$, 需要确定向下一时刻的状态过渡情况

记隐马尔可夫过程中，t 时刻从状态 $q_i$ 到 t+1 时刻 $q_j$ 的概率为 $a_{ij}$，即
$$P(i_{t+1}=q_j|i_t=q_i)=a_{ij}$$
且 $q_i,q_j\in Q$，对所有状态转换（概率），用矩阵A表示
$$A=[a_{ij}{]}_{N\times N},i,j=1,2,\cdots ,N$$
注：某时刻的状态只与前一时刻状态相关。

观测概率矩阵

选定了状态 $q_j$，在 $q_j$ 状态下，进行观察层的实验

在 t 时刻，处于状态 $q_j$ 的条件下，生成观测 $v_k$ 的概率用 $b_j(k)$ 表示
$$P(O_t=v_k|i_t=q_j)=b_j(k)$$
且 $v_k\in V,q_i\in Q$，对所有观测结果（概率），用矩阵B表示
$$B=[b_j(k){]}_{N\times M},k=1,2,\cdots ,M;j=1,2,\cdots ,N$$
马尔可夫模型

自此，由给定的初始状态向量$\pi$ 、状态转移概率矩阵A、观测概率矩阵B即可确定隐马尔可夫模型$\lambda$，即
$$\lambda =(A,B,\pi )$$

3.3.3 基本性质

• 隐马尔可夫过程的状态演变中，t 时刻的状态只与前时刻的状态相关，与其他时刻状态和观测无关
  $$P(i_t|i_{t-1},i_{t-2},\cdots ,i_1,o_{t-1},o_{t-2},\cdots ,o_1)=P(i_t|i_{t-1})$$
  该性质对应于状态转移概率矩阵

• 生成观测过程中，任意时刻的观测值只与该时刻选择的状态相关，与其他时刻状态和观测值无关
  $$P(o_t|i_T,\cdots ,i_t,i_{t-1},\cdots ,i_1,o_T,\cdots ,o_t,o_{t-1},\cdots ,o_1)$$
  该性质对应于观测概率矩阵。

3.4 图例示意

以具有马尔可夫过程的三硬币模型为例：

4. 模型求解

隐马尔可夫模型建立之后，又到了机器学习中喜闻乐见的问题求解过程。

值得说明的一点是，EM 算法是一种方法，可以用作为某一模型的学习算法，而隐马尔可夫模型是一个具体模型，并且是个生成模型，可以完成预测问题。且在模型问题求解的过程中，用到了 EM 算法这一方法思想。两者关系有着与朴素贝叶斯法（模型）和贝叶斯估计（方法）间关系异曲同工之处。

在完成预测问题的过程中，同之前 EM 算法模型求解过程一样，需要先构建极大似然函数，然后最大化似然函数来估计模型参数（之前EM算法推导止于此），最后根据已知参数的模型和观测序列来预测隐马尔可夫过程的状态序列。尽管前面部分跟之前求解过程相同，但实际求解计算，较之前基于EM算法的模型要复杂的多。

那么就对上述三个层层递进的基本问题进行求解：

• 概率问题：给定模型 $\lambda =(A,B,\pi )$ 和观测序列 $O=(o_1,o_2,\cdots ,o_T)$ ，计算似然函数 $P(O|\lambda )$
• 学习问题：极大化上述似然概率函数 $P(O|\lambda )$ ，即使用极大似然估计来估计模型参数
• 预测问题：根据得到的已知参数的模型 $\lambda$ 和观测序列 $O=(o_1,o_2,\cdots ,o_T)$ ，求解出与之对应的隐藏层最可能的状态序列 $I=(i_1,i_2,\cdots ,i_T)$

4.1 似然函数计算

给定模型 $\lambda =(A,B,\pi )$ 和观测序列 $O=(o_1,o_2,\cdots ,o_T)$ ，计算似然函数 $P(O|\lambda )$

4.1.1 直接计算

直接计算是基于穷举的算法思想。

不同于之前 EM 算法模型的一点在于，HMM 存在时序性，即状态序列 $I=(i_1,i_2,\cdots ,i_T)$ 是根据状态转移矩阵确定的。

对于已知观测序列 O，每个时刻下的观测值 $o_t$ 对应的状态 $i_t$ 取值都会有 N 种，即 $i_t\in Q=(q_1,q_2,\cdots ,q_N)$ ，那么对于整个观测序列 O 其实会对应着 $N^T$ 情况下的状态序列。

考虑对于每种状态序列（就假定为 $i_1,i_2,\cdots ,i_T$）都可以直接写出该状态序列似然概率为
$$P={\pi }_{i_1}{b}_{i_1}(o_1)a_{i_1{i}_2}{b}_{i_2}(o_2)\cdots a_{i_{T-1}{i}_T}{b}_{i_T}(o_T)$$

说明1

式子即为

$P=初始序列状态\times 初始观测值概率\times 转换到第二序列状态概率\times 第二观测值概率\times ......\times 转换到第T序列状态概率\times 第T观测值概率$

注意：在计算第二观测值$o_2$ 概率时，不是常规的 ${\pi }_{i_1}{a}_{i_1{i}_2}{b}_{i_2}(o_2)$，换句话说，到达第二序列的概率不是通过 ${\pi }_{i_1}{a}_{i_1{i}_2}$ 计算，因为这样就体现不出时序性，体现不出序列这个词的意义。

我们要的是一个过程，而非每个结果的堆积。

说明2

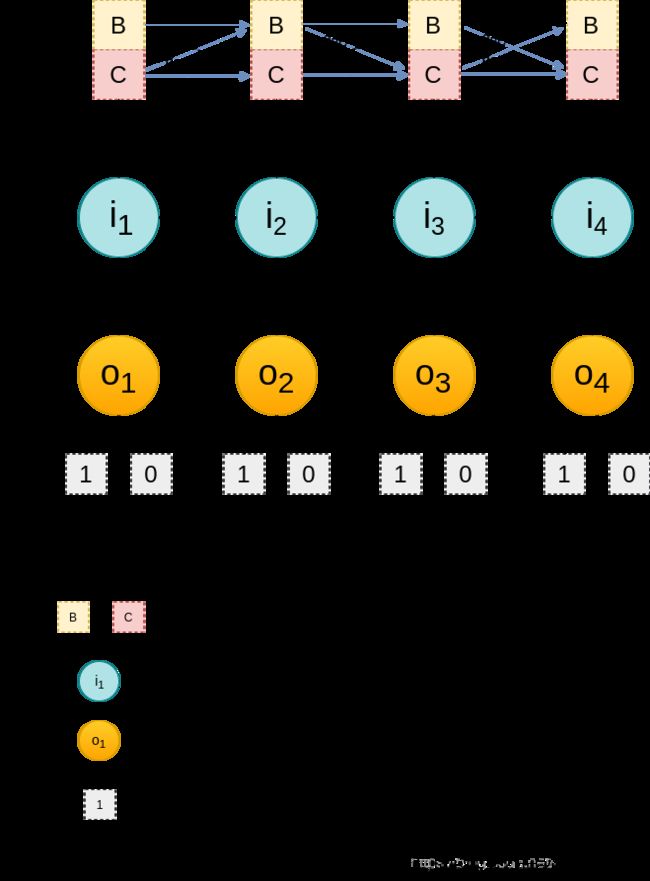
如上，对应于图例3.4中，黑色箭头引导的一条路径 (B->C->B->B)，即为一个可能的状态序列取值。且该序列取值的概率为
$$P={\pi }_B{a}_{BC}{a}_{CB}{a}_{BB}$$
其中：${\pi }_B$ 表示初始状态$i_1$ 为B的概率，$a_{BC}$ 表示从 B 转换为 C 的概率。

如果最终观测O序列取值为 （1,1,0,0），则可求出该种序列得到该种结果的概率为
$$P={\pi }_B\cdot b_B(1)\cdot a_{BC}\cdot b_C(1)\cdot a_{CB}\cdot b_B(0)\cdot a_{BB}\cdot b_B(0)$$
其中，$b_B(1)$ 表示 在选择投掷B的情况下，结果为正面的概率。

所有的状态序列，即是最上方四个时间段 {B,C} 的所有可能组合，有 $2\times 2\times 2\times 2=2^4$ 种

对所有可能的状态序列（$N^T$个）进行求和，即可得到最终的似然函数
$$P(O|\lambda )=\sum _{i_1,i_2,\cdots ,i_T\in Q}{\pi }_{i_1}{b}_{i_1}(o_1)a_{i_1{i}_2}{b}_{i_2}(o_2)\cdots a_{i_{T-1}{i}_T}{b}_{i_T}(o_T)$$
该种方法可能的状态序列个数为$N^T$，每个状态序列有 T 个元素，计算量可表示为 $O(T{N}^T)$。这种计算复杂度不能容忍的。但确实，该方法求解思想比较直接。

4.1.2 前向算法

事实上，在上面直接计算的过程中，可以感受到，有大量数据是重复计算的，而这也是使得计算效率较低的一个重要因素。

就拿状态序列取值来讲，以三个序列取值为例
$$\begin{gathered} (1)B\to C\to B\to B \\ (2)B\to C\to C\to B \\ (3)B\to C\to C\to C \end{gathered}$$
(1) 和 (2) 中前两个时刻序列取值是重复的，概率计算时，会重复计算；(2) 和 (3) 中前三个也是重复的，并且，对于前三个序列取值，只需在 (1) 中前两步 $B\to C$ 的基础上，再增加 C 取值即可，而不必从头计算。对于所有的 $N^T$ 个序列，类似重复计算的数量也是巨大的。

改进方法就是使用动态规划（DP）算法思想，即，将重复计算的值储存起来，下次使用时直接取值即可，而不重复计算。具体实现算法就是，前向算法。该算法是逐层计算，向后递推。

先定义根据时刻储存的、避免重复计算、可以递推的概率值：前向概率

具体为，对于给定模型，到某一时刻 t 部分观测序列为 $o_1,o_2,\cdots ,o_t$ ，且状态为 $q_i$ 的概率为前向概率 ${\alpha }_t(i)$ ，即
$$P(o_1,o_2,\cdots ,o_t,i_t=q_i)={\alpha }_t(i)$$
具体实现为：

• 求解第一层 (t=1)
  $${\alpha }_1(i)={\pi }_i{b}_i(o_1),i=1,2,\cdots ,N$$

• 向后逐层递推 $(t\to t+1)$
  $${\alpha }_{t+1}(i)=[\sum _{j=1}^N{\alpha }_t(j){\alpha }_{ji}]b_i(o_{t+1}),i=1,2,\cdots ,N$$

• 直到最后一层，得到最终结果

$$P(O|\lambda )=\sum _{i=1}^N{\alpha }_T(i)$$

以三硬币模型为例：（假设最终观测结果为 $o_1,o_2,o_3,o_4$ ）

算法过程如下：

• 计算第一层
  $$\begin{gathered} {\alpha }_1(B)={\pi }_B{b}_B(o_1) \\ {\alpha }_1(C)={\pi }_C{b}_C(o_1) \end{gathered}$$

• 向后递推（以递推到第二层为例）

$$\begin{gathered} {\alpha }_2(B)={\alpha }_1(B)a_{BB}{b}_B(O_2)+{\alpha }_1(C)a_{CB}{b}_B(o_2)=[\sum _{j\in B,C}{\alpha }_1(j)a_{jB}]b_B(o_2) \\ {\alpha }_2(C)={\alpha }_1(B)a_{BC}{b}_C(O_2)+{\alpha }_1(C)a_{CC}{b}_C(o_2)=[\sum _{j\in B,C}{\alpha }_1(j)a_{jC}]b_B(o_2) \end{gathered}$$

其中，${\alpha }_2(B)$ 储存了到第二层 B 状态的概率，${\alpha }_2(C)$ 储存了到达第二层 C 状态的概率，即包含了第二层所有情况，后续递推类似。

• 直到递推到最后一层，即可得到最终结果

该算法在两层递推时，计算量为 $N\times N=N^2$ 次（对应于上面图示的两层间的 2x2=4 个箭头指向），一共有 T 层，因此计算量表示为 $O(T{N}^2)$，相比较直接计算法，在一般 T 很大的情况下，少了很多计算量。

说明：AdaBoost 算法中也应用到了类似的思想。

4.1.3 后向算法

前向算法是从前向后递推，而后向算法是依据相同的思想，从后向前递推，步骤也很类似。

具体为，在时刻 t 状态为 $q_i$ 的条件下，从 $t+1$ 到 T 的部分观测序列为 $o_{t+1},o_{t+2},\cdots ,o_T$ 的概率为后向概率 ${\beta }_t(i)$
$${\beta }_t(i)=P(o_{t+1},o_{t+2},\cdots ,o_T|i_t=q_i)$$
实现为：

• 求解最后一层 (t=T)，
  $${\beta }_T(i)=1,i=1,2,\cdots ,N$$

• 向前逐层递推
  $${\beta }_t(i)=\sum _{j=1}^N{\alpha }_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j),i=1,2,\cdots ,N$$

• 直到第一层，乘上初始序列取值的概率
  $$P(O|\lambda )=\sum _{i=1}^N{\pi }_i{b}_i(o_1){\beta }_1(i)$$

同样以三硬币模型为例：（假设最终观测结果为 $o_1,o_2,o_3,o_4$ ）

算法过程如下：

• 最后一层 （t=4）
  $$\begin{gathered} {\beta }_4(B)=1 \\ {\beta }_4(C)=1 \end{gathered}$$
  该层没有实际意义，下面递推两层为例。

• 向前递推（递推到倒数第二层）

$$\begin{gathered} {\beta }_3(B)=a_{BB}{b}_B(o_4)+a_{BC}{b}_C(o_4) \\ {\beta }_3(C)=a_{CB}{b}_B(o_4)+a_{CC}{b}_C(o_4) \end{gathered}$$

• （递推到倒数第三层）
  $$\begin{gathered} {\beta }_2(B)=a_{BB}{b}_B(o_3){\beta }_3(B)+a_{BC}{b}_C(o_3){\beta }_3(C) \\ {\beta }_2(C)=a_{CB}{b}_B(o_3){\beta }_3(B)+a_{CC}{b}_C(o_3){\beta }_3(C) \end{gathered}$$
  其中，${\beta }_3(B)$ 储存了第三层到第四层的 $B\to B$ 和 $B\to C$ 过程，${\beta }_3(C)$ 储存了三四层的 $C\to B$ 和 $C\to C$ 过程，也即最后两层间的四个箭头。

${\beta }_2(B)$ 和 ${\beta }_2(C)$ 同理，储存了从第二层到第四层的所有过程，而这一计算需要第三层到第四层的过程结果，也即上述结果。

${\beta }_1(B)$ 和 ${\beta }_1(C)$， 储存了从第一层到第四层的所有过程，除去初始观察值的选择概率 ${\pi }_B{b}_B(o_1)$ 和 ${\pi }_C{b}_C(o_1)$。

• 最终结果，即在 ${\beta }_1(B)$ 和 ${\beta }_1(C)$ 基础上乘以初始概率
  $$P={\pi }_B{b}_B(o_1){\beta }_1(B)+{\pi }_C{b}_C(o_1)$$

前向与后向算法实际上是等价的。

4.2 模型参数估计

使用极大似然估计含有隐变量的HMM模型参数

4.2.1 Baum-Welch 算法

该算法本质上就是 EM 算法，确切地说，是EM算法在HMM模型上的具体应用。关于EM算法，具体可参考 EM 算法

算法过程：

• 初始化隐马尔可夫模型${\lambda }^{(0)}$的参数 $a_{ij}^{(0)},b_j(k{)}^{(0)},{\pi }_i^{(0)}$

• EM算法递推参数变化
  $$\begin{gathered} {\pi }_i^{(n+1)}=\frac{P(O,i_1=i)}{P(O)} \\ {a}_{ij}^{(n+1)}=\frac{\sum _{t=1}^{T-1}P(O,i_t=i,i_{t+1}=j)}{\sum _{t=1}^{T-1}P(O,i_t=i)} \\ {b}_j(k)=\frac{\sum _{t=1,o_t=v_k}^{T}P(O,i_t=j)}{\sum _{t=1}^{T}P(O,i_t=j)} \end{gathered}$$

• 迭代终止后，得到最终模型
  $${\lambda }^{(n+1)}=(A^{(n+1)},B^{(n+1)},{\pi }^{(n+1)})$$

4.3 状态序列预测

已知参数的模型 $\lambda =(A,B,\pi )$ 和观测序列 $O=(o_1,o_2,\cdots ,o_T)$ ，求解出与之对应的隐藏层最可能的状态序列 $I=(i_1,i_2,\cdots ,i_T)$

4.3.1近似算法

就是找每个时刻下状态取值中概率最大的那个，T个时刻组合起来就是结果。

根据前后向 ${\alpha }_t(i)，{\beta }_t(i)$ 定义，可以知道
$${\alpha }_t(i){\beta }_t(i)=P(i_t=q_i,O)$$
同样值得说明的是，之所以使用前后向概率来计算，是因为可以减少计算量。

全概率
$$P(O)=\sum _{i=1}^{N}P(i_t=q_i,O)=\sum _{i=1}^N{\alpha }_t(i){\beta }_t(i)$$
则在给定模型 $\lambda$ 和观测 O 的情况下，在时刻 t 处于状态 $q_i$ 的概率为 ${\gamma }_t(i)$
$${\gamma }_t(i)=P(i_t=q_i|O)=\frac{P(i_t=q_i,O)}{P(O)}=\frac{{\alpha }_t(i){\beta }_t(i)}{\sum _{i=1}^N{\alpha }_t(i){\beta }_t(i)}\text{\hspace{1em}(4.3.1)}$$
根据上式计算出每个时刻对应$q_i$（N个）的 ${\gamma }_t(i)$ ，取最大值，作为该时刻最可能的状态
$$i_t^{\ast }=\underset{i=1,2,\cdots ,N}{\mathrm{argmax}}[{\gamma }_t(i)]$$
最终得到状态序列
$$I^{\ast }=(i_1^{\ast },i_2^{\ast },\cdots ,i_T^{\ast })$$
该种做法局部割裂性的做法，还是由于HMM模型的时序性，确切说是转移矩阵（概率）的存在，使得该种结果并非一定是全局最优。

4.3.2 维特比算法

基于近似方法的缺点，去全面地考虑数据。最直接的方法是，穷举出所有可能序列，求出相应概率，概率最大的那个便是结果。但，这种做法同样存在计算量巨大的缺点，想法直接，却不可行。

类似地，依旧可以通过动态规划的思想来简化求解。其实该问题这就是动态规划常常用来解决的最优路径问题。在HMM模型中，使用DP求解该问题的方法叫 维特比算法。

可行性

对于最优路径来说，从 t=1 到 t=T ，需要确保每条子路径拿出来在该时间区间段，都是最优的。因此只需要从 t=1 开始递推计算路径概率值，根据概率值最大的选择节点，这些节点就是最终最优路径所经过的节点值。

注意点

直观上，在计算每层所有节点概率值后，直接取最大概率，从而确定该层节点。但实际上，并不是，由于转换概率的存在，在计算第 t 层所有节点概率值后，并不能确定本层该选取哪个节点，只能通过该层概率计算值确定上一层要选择的节点。因为，该层的转移概率还没有计算。

比较有趣的同直观想象不同的一点。

为了便于表达，该算法引入了两个变量，

t 时刻状态为 i 的所有单个路径中概率最大值记为 ${\delta }_t(i)$ ，即
$${\delta }_t(i)=\underset{i_1,i_2,\cdots ,i_{t-1}}{\max }P(i_t=i,i_{t-1},\cdots ,i_1,o_{t+1},\cdots ,o_1),i=1,2,\cdots ,N$$
t 时刻状态为 i 的所有单个路径中概率最大的路径的第 t-1 个节点记为 ${\varphi }_t(i)$， 且
$${\varphi }_t(i)={\mathrm{argmax}}_{1\le j\le N}[{\delta }_{t-1}(j)a_{ji}],i=1,2,\cdots ,N$$
算法过程为：

• 初始化（第一层）
  $$\begin{gathered} {\delta }_1(i)={\pi }_i{b}_i(o_1),i=1,2,\cdots ,N \\ {\varphi }_1(i)=0 \end{gathered}$$

• 递推计算${\delta }_t(i),{\varphi }_t(i)$
  $$\begin{gathered} {\delta }_t(i)={\max }_{1\le j\le N}[{\delta }_{t-1}(j)a_{ji}]b_i(o_t),i=1,2,\cdots ,N \\ {\varphi }_t(i)={\mathrm{argmax}}_{1\le j\le N}[{\delta }_{t-1}(j)a_{ji}],i=1,2,\cdots ,N \end{gathered}$$

• 选择每个时刻下概率最大对应的前一个节点作为最终最优路径的节点：递推终止和回溯确定路径 $I^{\ast }$

以上述三硬币模型为例，给定所有参数和观测序列，利用维特比算法求出最优路径。其中

初始状态概率向量为
$$\pi =(0.5,0.5{)}^T$$

转换概率矩阵为
$$A=\left[\begin{array}{cc}0.9& 0.1\\ 0.3& 0.7\end{array}\right]$$
观测概率矩阵为
$$B=\left[\begin{array}{cc}0.4& 0.6\\ 0.8& 0.2\end{array}\right]$$
观测序列为
$$O=(1,1,1,0)$$
求解过程如下：

t=1
$$\begin{gathered} {\delta }_1(B)={\pi }_B{b}_B(o_1)=0.5\times 0.6=0.3 \\ {\delta }_1(C)={\pi }_C{b}_C(o_1)=0.5\times 0.8=0.4 \end{gathered}$$
t=2
$$\begin{gathered} {\delta }_2(B)=max\{{\delta }_1(B)a_{BB},{\delta }_1(C)a_{CB}\}{b}_B(o_2)=max\{0.3\times 0.9,0.4\times 0.3\}\times 0.4=0.108 \\ {\delta }_2(C)=max\{{\delta }_1(B)a_{BC},{\delta }_1(C)a_{CC}\}{b}_C(o_2)=max\{0.3\times 0.1,0.4\times 0.7\}\times 0.8=0.224 \end{gathered}$$
最大值计算路径为 ${\delta }_1(B)a_{BC}{b}_C(o_2)=0.224$ ，即$B\to C$，确定第一个节点为 B

t=3
$$\begin{gathered} {\delta }_3(B)=max\{{\delta }_2(B)a_{BB},{\delta }_2(C)a_{CB}\}{b}_B(o_3)=max\{0.108\times 0.9,0.224\times 0.3\}\times 0.4=0.03888 \\ {\delta }_3(C)=max\{{\delta }_2(B)a_{BC},{\delta }_2(C)a_{CC}\}{b}_C(o_3)=max\{0.108\times 0.1,0.224\times 0.7\}\times 0.8=0.12544 \end{gathered}$$
最大计算路径为 ${\delta }_2(C)a_{CC}{b}_C(o_2)=0.12544$， 即$B\to C\to C$，确定第二个节点为 C

t=4
$$\begin{gathered} {\delta }_4(B)=max\{{\delta }_3(B)a_{BB},{\delta }_3(C)a_{CB}\}{b}_B(o_4)=max\{0.03888\times 0.9,0.12544\times 0.3\}\times 0.6=0.0225792 \\ {\delta }_4(C)=max\{{\delta }_3(B)a_{BC},{\delta }_3(C)a_{CC}\}{b}_C(o_4)=max\{0.03888\times 0.1,0.12544\times 0.7\}\times 0.2=0.0175616 \end{gathered}$$
最大计算路径为 ${\delta }_3(C)a_{CB}{b}_B(o_4)=0.0225792$ ，即 $B\to C\to C\to B$ ，确定第三、四个节点C、B

因此最终最可能状态序列为 $I=(B,C,C,B)$

5. 代码实现

每个算法的实现都不算太难，实现关键在于一些公式的递推计算。

挖坑，有时间再填

博客字数和用时又创新高，完结撒花