EM算法在GMM中的应用与python实现

---

一、混合高斯分布

1-1 GMM概要

在k-means中，每个数据样本属于某一个cluster，比如对于第1个数据，可以通过$r_1=(0,1,0)$中的指示变量0,1来明确指出该数据属于哪个cluster。关于k-means可以参考我的另一篇博客。

在混合高斯分布(Gaussian Mixture Mode:GMM)中，每个数据样本也是属于某一个cluster，但它的指示变量不再是2元的01，而是用概率来表示，或者说用隐变量来表示。举个例子，数据$x_1$对应的隐变量为$z_1$，他的期望值可以表示为$E[z_1]=(0.7,0.2,0.1)$，即$0<=z_{1k}<=1$。

下面的推导中会用到以下数学符号：

• $x$: $D$ 维度的随机变量
• $z$: $k$维度的随机变量，也是模型的隐变量
• $X=\{x_1,x_2,...,x_N\}$: $N$个数据观测数据
• $K$: cluster（聚类）的个数，已知

首先是GMM的概率密度函数：
$$p(x|\pi ,\mu ,\Sigma )=\sum _{k=1}^K{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)$$
可以明显看到，这是$K$个高斯分布按比例加权求和的结果。下面用以3个1维高斯分布为例来说明：

import numpy as np
import matplotlib.pyplot as plt

K = 3
n = 301
mu = [-2, 0 ,2]
sigma = [0.5, 0.7, 1.5]
pi = [0.2, 0.3, 0.5]
intervals = np.linspace(-4, 7, n)

pdfs = np.zeros(shape = [n, K])
mix_pdf = np.zeros(shape = [n])
for k in range(K):
  pdfs[:, k] = pi[k] * 1/(np.math.sqrt(2*np.math.pi)*sigma[k]) * np.exp(-(intervals-mu[k])**2 / (2*sigma[k]**2))
  mix_pdf += pdfs[:, k]

plt.figure()
for k in range(K):
  plt.plot(np.linspace(-4,7,n), pdfs[:, k])
plt.show()

plt.figure()
plt.plot(intervals, mix_pdf, c = "r")
plt.show()

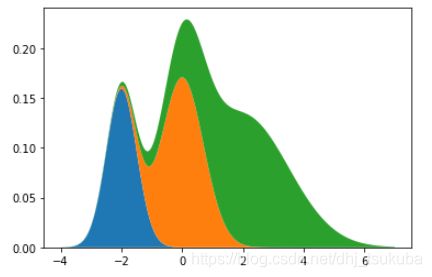
下图表示3个1维单高斯分布的概率密度函数（还没有混合），其每个高斯分量的分配比例为$\pi =(0.2,0.3,0.5)$, 该比例同时也是每个高斯分量的积分结果，也就是其包围的面积。

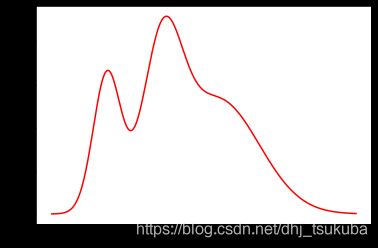
混合之后得到的混合高斯分布概率密度函数如下图所示，积分结果为1。

1-2 由边缘概率引出的隐变量

如果用$p(x)$表示某一数据的分布，我们可以通过边缘概率的计算和乘法公式导出该$p(x)$
$$p(x)=\sum _{z}p(x,z)dz=\sum _{z}p(x|z)p(z)dz...(1)$$
下面我们重点讨论一下这里的$p(z)$和$p(x|z)$.

首先我们引入变量$z_k$，这里的$z_k$可以参考k-means中的$r_{nk}$，如果第$n$个数据样本属于$k$类，则$r_{nk}=1$，而这里的$z_k$用随机变量$\{0,1\}$表示，$z_k\in \{0,1\}$ 并且 ${\sum }_k{z}_k=1$
我们考虑隐变量集合$z=\{z_1,z_2,...z_k,...,z_K\}$中的$z_k$，$z_k$为1 的概率由混合系数${\pi }_k$来决定：
$$p(z_k=1)={\pi }_k$$
很明显，${\pi }_k$满足 $0\le {\pi }_k\le 1$以及 ${\sum }_{k=1}^K{\pi }_k=1$， 那么$p(z)$就可以表示为：
$$p(z)=\prod _{k=1}^K{\pi }_k^{z_k}$$

同时，在给定$z$的条件下我们可以求得数据$x$的条件概率分布，具体来讲，就是在给定条件$z_k=1$的条件下，$x$服从第$k$个(高维或者1维)高斯分布：
$$p(x|z_k=1)=N(x|{\mu }_k,{\Sigma }_k)$$
结合上面的$p(z)={\prod }_{k=1}^K{\pi }_k^{z_k}$，我们可以得到：
$$p(x|z)=\prod _{k=1}^{K}N(x|{\mu }_k,{\Sigma }_k{)}^{z_k}$$
将这里的$p(z)$，$p(x|z)$带入到(1)中，我们可以得到：
$$p(x)=\sum _{z}p(x|z)p(z)dz=\sum _{k=1}^K{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)$$
可以发现这个式子和混合高斯分布是一样的。

1-3 隐变量后验概率

我们可以通过$p(z)$和$p(x|z)$，结合贝叶斯公式算出$z$的后验概率$p(z|x)$，即可以通过观测数据$x$得到$z$的分布：
$$\begin{gathered} p(z_k=1|x)=\frac{p(x,z_k=1)}{p(x)}=\frac{p(z_k=1)p(x|z_k=1)}{{\sum }_{j=1}^{K}p(z_j=1)p(x|z_j=1)} \\ =\frac{{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x|{\mu }_j,{\Sigma }_j)} \end{gathered}$$
这里的$p(x|z_k=1)$是似然，$p(z_k=1)$是先验概率， 分母是边缘概率。
我们可以将这个后验概率理解为，在已知的某个数据点上，混合高斯分布概率密度函数中各个$k$类分布所占的比例，用$\gamma (z_k)$来表示，通过下图更容易理解：

1-4 完整数据集合以及不完整数据集合

这里的不完整数据集表示只有数据，但不知道哪一部分数据属于哪个分布，因此联合概率分布$p(x,z)$无法计算，如下图所示：

相对的，完整数据集表示各个分布的参数都是已知的并且知道哪一部分数据属于哪个分布，可以计算出$p(x,z)$，如下图所示：

EM算法就是用来推测$z$的分布参数的，从不完整数据集得到完整数据集。

1-5 最大似然估计

$z$的分布参数由$\theta$表示，服从$p(x|\theta )$生成的$N$个数据用$D=\{x_1,x_2,...,x_N\}$来表示，找到生成这组数据的最优参数$\theta$的方法就是最大似然估计。将$\theta$作为变量的概率称为似然，$p(x|\theta )$被称为似然函数，找到使似然最大的参数$\theta$称为最大似然估计。

二、推导

2-1 EM在GMM中的应用

首先列出公式中用到的符号：

$x$: $d$维数据
$D=\{x_1,x_2,x_3,...,x_N\}$: $N$个观测数据
$X=\left[\begin{array}{c}{x}_1^T\\ x_2^T\\ ...\\ x_N^T\end{array}\right]$: $N$个观测数据组成的矩阵($N\times D$)
$K$: 聚类数
$z$: 隐变量，表示某个观测数据是否属于$k$类，$K$维
$Z=\left[\begin{array}{c}{z}_1^T\\ z_2^T\\ ...\\ z_N^T\end{array}\right]$: $N$个隐变量的矩阵($N\times K$)

观测N个数据时，混合高斯分布的对数似然函数：

$$\begin{gathered} lnp(x|\pi ,\mu ,\Sigma )=ln\prod _{n=1}^N\{\sum _{k=1}^K{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)\} \\ =\sum _{n=1}^{N}ln\{\sum _{k=1}^K{\pi }_{k}N(x_n|{\mu }_k,{\Sigma }_k)\} \end{gathered}$$

该对数似然函数就是我们需要优化的对象，这里的 $ln$ 对数部分很难求解析解，因此我们需要用以迭代法为基础的EM算法来求解。
下面给出EM算法的整体思路：

1. 初始化： 对需要优化的对象参数$\pi$,$\mu$,$\Sigma$进行初始化赋值，然后计算出对数似然函数的结果
2. E-step：计算后验概率$\gamma (z_{nk})$
3. M-step：将对数似然函数关于$\pi$,$\mu$,$\Sigma$偏微分置为0，求参数最优解
4. 收敛判断：再次计算对数似然函数，设定一个阈值，如果与前一次的差值小于该阈值则判断为收敛，停止迭代更新，否则从M-step开始循环

2-1-1 $\mu$最优解

首先我们对$lnN(x|\mu ,\Sigma )$关于$\mu$求偏微分，这里会用到矩阵求微分的公式，同时我们假设协方差矩阵$\Sigma$为对角阵，即数据之间相互独立
$$\frac{\partial }{\partial x}{x}^{T}Ax=(A+A^T)x$$
下面开始求偏微分：

$$\begin{array}{rl}& \frac{\partial }{\partial \mu }lnN(x|\mu ,\Sigma )\\ =& \frac{\partial }{\partial \mu }ln\frac{1}{(2\pi {)}^{\frac{d}{2}}{\Sigma }^{\frac{1}{2}}}exp[-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )]\\ =& \frac{\partial }{\partial \mu }[-\frac{d}{2}ln(2\pi )-\frac{1}{2}ln|\Sigma |-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )]\\ =& \frac{\partial }{\partial \mu }[-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )]\\ =& (-1)(-\frac{1}{2})({\Sigma }^{-1}+({\Sigma }^{-1}{)}^T)(x-\mu )\\ =& {\Sigma }^{-1}(x-\mu )\end{array}$$

$\mu$的最大化，下面的$N_{nk}=N(x_n|{\mu }_k,{\Sigma }_k)$，对数似然函数 $L=lnp(X|\pi ,\mu ,\Sigma )$
这里涉及到对数函数求微分：$(lnf{)}^{{}^{\prime }}=\frac{f^{{}^{\prime }}}{f}$
$$\frac{\partial }{\partial \mu }N=N(\frac{\partial }{\partial \mu }lnN)=N{\Sigma }^{-1}(x-\mu )$$
$$\begin{array}{rl}& \frac{\partial }{\partial {\mu }_k}L\\ =& \frac{\partial }{\partial {\mu }_k}\sum _{n=1}^{N}ln\{\sum _{j=1}^K{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)\}\\ =& \sum _{n=1}^N\frac{{\pi }_k\frac{\partial }{\partial {\mu }_k}{N}_{nk}}{{\sum }_{j=1}^K{\pi }_j{N}_{nj}}=\sum _{n-1}^N\frac{{\pi }_k{N}_{nk}{\Sigma }_k^{-1}(x_n-{\mu }_k)}{{\sum }_{j=1}^K{\pi }_j{N}_{nj}}\\ =& \sum _{n=1}^N\frac{{\pi }_k{N}_{nk}}{{\sum }_{j=1}^K{\pi }_j{N}_{nj}}{\Sigma }_k^{-1}(x_n-{\mu }_k)\\ =& {\Sigma }_k^{-1}\sum _{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)\end{array}$$

下面将该微分置为0求${\mu }_k$的最大值：
$$\begin{gathered} \sum _{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)=0 \\ \sum _{n=1}^N\gamma (z_{nk})x_n-{\mu }_k\sum _{n=1}^N\gamma (z_{nk})=0 \\ {\mu }_k=\frac{{\sum }_{n=1}^N\gamma (z_{nk})x_n}{{\sum }_{n=1}^N\gamma (z_{nk})}=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{nk})x_n \end{gathered}$$

2-1-2 $\Sigma$最优解

和求${\mu }_k$一样，这里先求$lnN(x|\mu ,\Sigma )$对$\Sigma$的微分，推导中利用了矩阵论中二次型和trace的关系：
$x^{T}Ax=tr(Ax{x}^T)$，矩阵对数的微分(对称矩阵)：$\frac{\partial }{\partial A}ln|A|=(A^{-1}{)}^T=A^{-1}$，trace求微分：
$\frac{\partial }{\partial A}tr(A^{-1}B)=-(A^{-1}B{A}^{-1}{)}^T$
$$\begin{array}{rl}lnN& =-\frac{D}{2}ln(2\pi )-\frac{1}{2}ln|\Sigma |-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\\ & =-\frac{D}{2}ln(2\pi )-\frac{1}{2}ln|\Sigma |-\frac{1}{2}tr({\Sigma }^{-1}(x-\mu )(x-\mu {)}^T)\end{array}$$
$$\frac{\partial }{\partial \Sigma }(lnN)=-\frac{1}{2}{\Sigma }_k^{-1}+\frac{1}{2}({\Sigma }_k^{-1}(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T{\Sigma }_k^{-1})$$
下面对对数似然函数求关于${\Sigma }_k$的微分：
$$\begin{array}{rl}& \frac{\partial }{\partial {\Sigma }_k}L\\ =& \frac{\partial }{\partial {\Sigma }_k}\sum _{n=1}^{N}ln\{\sum _{j=1}^K{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)\}\\ =& \sum _{n=1}^N\frac{{\pi }_k\frac{\partial }{\partial {\Sigma }_k}{N}_{nk}}{{\sum }_{j=1}^K{\pi }_j{N}_{nj}}=\sum _{n-1}^N\frac{{\pi }_k{N}_{nk}\frac{\partial }{\partial {\Sigma }_k}ln{N}_{nk}}{{\sum }_{j=1}^K{\pi }_j{N}_{nj}}\\ =& \sum _{n-1}^N\frac{{\pi }_k{N}_{nk}}{{\sum }_{j=1}^N{\pi }_j{N}_{nj}}\{-\frac{1}{2}{\Sigma }_k^{-1}+\frac{1}{2}({\Sigma }_k^{-1}(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T{\Sigma }_k^{-1})\}\end{array}$$
将该微分置0，提出${\Sigma }_k^{-1}$：
$$\begin{gathered} ({\Sigma }_k^{-1})\sum _{n=1}^N\gamma (z_{nk})\{I-(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T{\Sigma }_k^{-1}\}= \\ \sum _{n=1}^N\gamma (z_{nk})=\sum _{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T{\Sigma }_k^{-1} \\ {\Sigma }_k=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T \end{gathered}$$

2-1-3 $\pi$最优解

和前面的2个参数不同，对于$\pi$有这样一个限制：${\sum }_{k=1}^K{\pi }_k=1$，求限制条件下的最优解需要用到拉格朗日乘数法，朗格朗日乘子用$\lambda$表示，需要求最优解的函数用下式表示：
$$G=L+\lambda (\sum _{k=1}^K{\pi }_k-1)$$
这里的$L$代表对数似然函数
$$\begin{array}{rl}\frac{\partial }{\partial {\pi }_k}G=& \frac{\partial }{\partial {\pi }_k}\sum _{n=1}^{N}ln\{\sum _{j=1}^K{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)\}+\frac{\partial }{\partial {\pi }_k}\lambda (\sum _{k=1}^K{\pi }_k-1)\\ =& \sum _{n=1}^N\frac{N_{nk}}{{\sum }_{j=1}^K{\pi }_j{N}_{nj}}+\lambda =\sum _{n=1}^N\frac{{\pi }_k}{{\pi }_k}\frac{N_{nk}}{{\sum }_{j=1}^K{\pi }_j{N}_{nj}}+\lambda \\ =& \frac{1}{{\pi }_k}\gamma (z_{nk})+\lambda =\frac{N_k}{{\pi }_k}+\lambda =0\\ N_k=& -\lambda {\pi }_k\\ N=& \sum _{k=1}^K{N}_k=-\lambda \sum _{k=1}^K{\pi }_k=-\lambda \\ {\pi }_k=& \frac{N_k}{-\lambda }=\frac{N_k}{N}\end{array}$$

2-2 通过EM算法对混合高斯模型进行参数估计

1. 初始化： 对需要优化的对象参数$\pi$,$\mu$,$\Sigma$进行初始化赋值，然后计算出对数似然函数的结果
2. E-step：计算后验概率$\gamma (z_{nk})$

$$\begin{array}{rl}\gamma (z_{nk})=& p(z_k=1|x)\\ =& \frac{p(z_k=1)p(x|z_k=1)}{{\sum }_{j=1}^{K}p(z_k=1)p(x|z_k=1)}\\ =& \frac{{\pi }_{k}N(x|{\mu }_k,{\Sigma }_k)}{{\sum }_{j=1}^K{\pi }_{j}N(x|{\mu }_j,{\Sigma }_j)}\end{array}$$

3. M-step：将对数似然函数关于$\pi$,$\mu$,$\Sigma$偏微分置为0，求参数最优解

$$\begin{gathered} {\mu }_k^{\ast }=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{nk})x_n \\ {\Sigma }_k^{\ast }=\frac{1}{N_k}\sum _{n=1}^N\gamma (z_{nk})(x_n-{\mu }_k)(x_n-{\mu }_k{)}^T \\ {\pi }_k=\frac{N_k}{N}=\frac{{\sum }_{n=1}^N\gamma (z_{nk})}{N} \end{gathered}$$

4. 收敛判断：再次计算对数似然函数，设定一个阈值，如果与前一次的差值小于该阈值则判断为收敛，停止迭代更新，否则从M-step开始循环

$$\begin{gathered} L_{new}=lnp(X|\pi ,\mu ,\Sigma )=\sum _{n=1}^{N}ln\{\sum _{j=1}^K{\pi }_{j}N(x_n|{\mu }_j,{\Sigma }_j)\} \\ {L}_{new}-L_{old}<ϵ \end{gathered}$$

三、python代码实现

具体的代码实现可以参考我的github，这里只贴出一部分核心代码

def plot_gmm_contour(mu, sigma, pi, K):
  X, Y = np.meshgrid(np.linspace(x_min, x_max), np.linspace(y_min, y_max))
  XX = np.array([X.ravel(), Y.ravel()]).T
  Z = np.sum(np.array([[pi[k] * st.multivariate_normal.pdf(d, mu[k], sigma[k]) for k in range(K)] for d in XX]), axis = 1)
  Z = Z.reshape(X.shape)
  CS = plt.contour(X, Y, Z, alpha = 0.5, zorder = -100)
  plt.title("pdf contour of a GMM")

# EM iteration
def iterate(step):
  global mu, sigma, pi
  plt.clf()
  print("step: {}".format(step))
  if step <= 3:
    print("initial state")
    plt.scatter(data[:, 0], data[:, 1], s = 30, c = "gray", alpha = 0.5, marker = "+")
    for i in range(3):
      plt.scatter(mu[i, 0], mu[i, 1], c = c[i], marker = "o", edgecolors = "k", linewidths = 1)
    plot_gmm_contour(mu, sigma, pi, K)
    plt.title("inital state")
    return
  
  # E step
  likelihood = likelihood_cal(data, mu, sigma, pi, K)
  gamma = (likelihood.T / np.sum(likelihood, axis = 1)).T
  N_k = [np.sum(gamma[:, k]) for k in range(K)]

  # M step
  # pi
  pi = N_k / N

  # mu
  mu_tmp = np.zeros(shape = [K, D])
  for k in range(K):
    for i in range(len(data)):
      mu_tmp[k] += gamma[i, k] * data[i]
    mu_tmp[k] /= N_k[k]
  mu_prev = mu.copy()
  mu = mu_tmp.copy()
  print("updated mu:\n{}".format(mu))

  # sigma
  sigma_tmp = np.zeros(sigma.shape)
  for k in range(K):
    for i in range(len(data)):
      sigma_tmp[k] += gamma[i, k] * np.dot((data[i] - mu[k])[:, np.newaxis], (data[i] - mu[k])[:, np.newaxis].T)
    sigma_tmp[k] /= N_k[k]
  sigma_prev = sigma.copy()
  sigma = sigma_tmp.copy()
  print("updated sigma:\n{}".format(sigma))

  # update likelihood
  sum_log_likelihood_prev = np.sum(np.log(likelihood))
  sum_log_likelihood = np.sum(np.log(likelihood_cal(data, mu, sigma, pi, K)))

  diff = sum_log_likelihood - sum_log_likelihood_prev
  print("sum log likelihood: {}".format(sum_log_likelihood))
  print("diff: {}".format(diff))

  for i in range(np.sum(n)):
    plt.scatter(data[i, 0], data[i, 1], s = 30, c = c[np.argmax(gamma[i])], alpha = 0.5, marker = "+")
  
  for k in range(K):
    ax = plt.axes()
    ax.arrow(mu_prev[k, 0], mu_prev[k, 1], mu[k, 0] - mu_prev[k, 0], mu[k, 1] - mu_prev[k, 1], lw = 0.8, head_width = 0.02, head_length = 0.02, fc = "k", ec = "k")
    plt.scatter(mu_prev[k, 0], mu_prev[k, 1], c = c[k], marker = "o", alpha = 0.8)
    plt.scatter(mu[k, 0], mu[k, 1], c = c[k], marker = "o", edgecolors = "k", linewidths = 1)
  # plt.title("steps: {}".format(step))

  plot_gmm_contour(mu, sigma, pi, K)

  if np.abs(diff) < 0.0001:
    plt.title("likelihood converged")
  else:
    plt.title("step: {}".format(step))

迭代的动态过程如下所示：