EM算法和GMM

最近在学习Andrew Ng 教授的机器学习课件。第7和第8章，主要讲解EM算法和GMM。论文讲解浅显易懂，但有些内容不完整。比如，没有写出来协方差 Σ 的求解过程，没有具体的实例应用。本文在原论文的基础上，增加了协方差的求解过程，和使用GMM进行聚类的Python代码。

1。Jensen不等式
回顾优化理论的一些概念。设f是定义域为实数的函数，如果对于所有实数x， f′′≥0 ，那么f是凸函数。当x是向量时，如果其Hessian矩阵H是半正定的( H≥0 )，那么f是凸函数。如果 f′′>0 或者 H>0 ， 那么f是严格凸函数。

定义:假设f是一个凸函数，X是一个随机变量。那么

E[f(X)]≥f(E(X))

此外，如果f是严格凸函数，那么当且仅当 X=E(X) (即X为常数)时， E(f(X))=f(E(X)) 。

2.EM算法
给定训练样本 {x(1),x(2),…,x(m)} ，样例之间相互独立。我们想找到每个样例的类别z，能使得 p(x,z) 最大。 p(x,z) 的最大似然估计为：

L(θ)=∑i=1mlogp(x;θ)=∑i=1mlog∑zp(x,z;θ)

直接求解该公式，比较困难。因为有隐变量的存在。所以一种方法是先确定z，在求解。

EM算法提供了一种近似计算含有隐变量概率模型的极大似然估计的方法，EM算法的最大优点是简单性和普适性。下面介绍EM算法的推到过程。

对于每个样例i，让 Qi 表示该样例隐变量z的某种分布。 Qi 满足 ∑zQi(z)=1 和 Qi(z)≥0 。则由Jensen不等式可以得到:

L(θ)=∑i=1mlogp(x(i);θ)=∑i=1mlog∑z(i)p(x(i),z(i);θ)=∑i=1mlog∑z(i)Qi(z(i))p(x(i),z(i);θ)Qi(z(i))≥∑i=1m∑z(i)Qi(z(i))logp(x(i),z(i);θ)Qi(z(i))=J(θ)

其中，

∑z(i)Qi(z(i))p(x(i),z(i);θ)Qi(z(i))

就是 [p(x(i),z(i);θ)/Qi(zi)] 的期望。

J(θ) 可以看做是 L(θ) 的一个下界。对于任意的分布 Qi(z) 都是成立的。那么我们应该选择哪一种分布呢。一种思想是我们应该选择最接近 L(θ) 的分布。即使得Jensen不等式的等号成立时的分布。由以上定义可知，Jensen不等式等号成立的条件是 X 是一个常数。即

p(x(i),z(i);θ)Qi(z(i))=constant

由上式得到：

Qi(z(i))=c∗p(x(i),z(i);θ)

其中，c为系数。因为 ∑zQi(z)=1 .。 所以有

∑zc∗p(x(i),z(i);θ)=1

,
得到 c=1/p(x(i);θ) 。 则

Qi(z(i))=p(x(i),z(i);θ)p(x(i);θ)=p(z(i)|x(i);θ)

因此， J(θ) 可以表示为

J(θ)=∑i=1m∑zp(z(i)|x(i);θ)logp(x(i),z(i);θ)p(z(i)|x(i);θ)

EM算法步骤
求E步：

Qi(z(i))=p(z(i)|x(i);θ)

求M步：

θ=argmaxθ∑i=1m∑z(i)Qi(z(i))logp(x(i),z(i);θ)Qi(z(i))

3.单调性
假设 L(θt) 为

L(θt)=∑i=1m∑z(i)Qti(z(i))logp(x(i),z(i);θt)Qti(z(i))

则根据公式，我们有

L(θt+1)≥∑i=1m∑z(i)Qti(z(i))logp(x(i),z(i);θt+1)Qti(z(i))≥∑i=1m∑z(i)Qti(z(i))logp(x(i),z(i);θt)Qti(z(i))=L(θt)

第一个 ≥ 是由 L(θ)≥J(θ) 决定的。第二个 ≥ 是由最大化决定的。第三个等号是Jensen不等式的等号成立的条件。

3.高斯混合模型
多元高斯函数的分布函数如下：

N(x;μ,Σ)=1(2π)d/2|Σ|1/2exp(−12(x−μ)TΣ−1(x−μ))

其中，d为维数，x为列向量。
假设高斯混合模型由k个分量组成，每个分量都是多元高斯分布。则高斯混合模型(GMM)的概率密度为：

P(x;π,μ,Σ)=∑j=1kπjN(x;μj,Σj)

其中， π≥0 ，且 ∑kj=1πj=1 。

我们假设

w(i)j=Qi(z(i)=j)=p(z(i)=j|x(i);π,μ,Σ)

其中， w(i)j 表示在概率分布 Qi 下 z(i) 选择j的概率。
目标函数为

J(π,μ,Σ)=∑i=1m∑z(i)Qi(z(i))logp(x(i),z(i);π,μ,Σ)Qi(z(i))=∑i=1m∑j=1kQi(z(i)=j)logp(x(i)|z(i)=j;μ,Σ)p(z(i)=j;π)Qi(z(i)=j)=∑i=1m∑j=1kw(i)jlog1(2π)d/2|Σ|1/2exp(−12(x(i)−μj)TΣ−1j(x(i)−μj))∗πjw(i)j

求 J 对μl的偏导数为

∇μlJ(π,μ,Σ)=∇μl∑i=1m∑j=1kw(i)jlog1(2π)d/2|Σ|1/2exp(−12(x(i)−μj)TΣ−1j(x(i)−μj))∗πjw(i)j=−∇μl∑i=1m∑j=1kw(i)j12(x(i)−μj)TΣ−1j(x(i)−μj)=12∑i=1mw(i)j∇μl(2∗μTlΣ−1lx(i)−μTlΣ−1lμl)=∑i=1mw(i)j(Σ−1lx(i)−Σ−1lμl)

让上式等于0，可以得到

μl=∑mi=1w(i)x(i)l∑mi=1w(i)l

接下来求解 Σ 。在求解之前，我们需要两个公式，这两个公式可以在文献[1]的第5章找到。

∂tr(AW−1B)∂W=−(W−1BAW−1)T

∂|W|∂W=|W|(W−1)T

根据上式，我们有

∇ΣlJ(π,μ,Σ)=∇Σl∑i=1m∑j=1kw(i)jlog1(2π)d/2|Σ|1/2exp(−12(x(i)−μj)TΣ−1j(x(i)−μj))∗πjw(i)j=−12∑i=1mw(i)j∇Σl(log|Σl|+(x(i)−μl)TΣ−1l(x(i)−μl))=−12∑i=1mw(i)j((Σ−1)T−(Σ−1l(x(i)−μl)(x(i)−μl)TΣ−1l)T)=0

对于等式

−12∑i=1mw(i)j((Σ−1)T−(Σ−1l(x(i)−μl)(x(i)−μl)TΣ−1l)T)=0

两边同时转置，左乘和右乘 Σl ，约减之后得到

∑i=1mw(i)j(Σl−(x(i)−μl)(x(i)−μl)T)=0

最后得到:

Σl=∑mi=1w(i)j(x(i)−μl)(x(i)−μl)T∑mi=1w(i)j

对于 π ，因为 ∑kj=1πj=1 。 所以使用拉格朗日乘子法得到

L(π)=∑i=1m∑j=1kw(i)jlogπj+β(∑j=1kπj−1)

求偏导得到

∂L(π)∂πj=∑i=1mw(i)jπj+β

让上式等于0，得到

πj=∑mi=1w(i)j−β

因为 ∑kj=1πj=1 , 因此有 −β=∑mi=1∑kj=1w(i)j=∑mi=11=m .最终有

πj=1m∑i=1mw(i)j

其中， w(i)j=Qi(z(i)=j) 求解方式为

Qi(z(i)=j)=p(z(i)=j|x(i);π,μ,Σ)=p(x(i)|z(i)=j;μ,Σ)p(z(i)=j;π)∑kl=1p(x(i)|z(i)=l;μ,Σ)p(z(i)=j;π)=πjN(x(i);μj,Σj)∑kl=1πlN(x(i);μl,Σl)

GMM的一个主要应用是聚类。在聚类中，每个高斯模型就是一个类别。下面，我们给出了一个简单的聚类的例子。代码用python写的。

# -*- coding: utf-8 -*-
"""
Created on Tue Jan 16 11:31:19 2018

@author: lanlandetian
"""

import numpy as np
from numpy import linalg
import matplotlib.pyplot as plt


def loadData():
    mean1 = [0,0]
    cov1 = [[1,0.5], [0.5,1]]

    mean2 = [5,5]
    cov2 = [[1,0], [0,1]]

    mean3 = [-5,1]
    cov3 = [[5,0], [0,5]]

    X = np.random.multivariate_normal(mean1,cov1,100)
    a = np.random.multivariate_normal(mean2,cov2,100)
    b = np.random.multivariate_normal(mean3,cov3,100)
    X = np.concatenate((X,a,b),axis = 0)

    return X

#多元高斯函数
def gaussian(x,mu,sigma):
    alpha = 0.1
    d = len(x)
    n = np.shape(sigma)[0]
    ex = - 1/2 * (np.mat(x - mu) * np.mat(linalg.inv( sigma + alpha * np.eye(n,n) )) \
    * np.mat(x - mu).T)[0,0]
    determinant = linalg.det(sigma)
    ret = 1 / ( np.power((2*np.pi),d/2) * np.power(determinant, 1/2) ) * np.exp(ex)
    return ret

#目标函数
def Loss(X,k,pi,mu,sigma):
    [m,n] = np.shape(X)
    W = np.zeros((m,k))
    #求解W
    for i in range(0,m):
        total = 0
        for j in range(0,k):
            total += pi[j]*gaussian(X[i],mu[j],sigma[j])

        for j in range(0,k):
            W[i,j] = pi[j]*gaussian(X[i],mu[j],sigma[j]) / total

    ret = 0
    for i in range(0,m):
        for j in range(0,k):
            ret += W[i,j]* np.log(pi[j]*gaussian(X[i],mu[j],sigma[j]) / W[i,j])

    return ret

#EM算法主函数
def EM(X,k = 3,iter = 50):
    [m,n] = np.shape(X)
    #初始化参数
    pi = np.array([0.1,0.5,0.4])
    mu = np.array([[0,0],
                   [1,5],
                   [-5,3]])
    sigma = np.zeros((k,n,n))
    sigma[0] = np.array([[1,0.5],[0.5,1]])
    sigma[1] = np.array([[3,0],[0,3]])
    sigma[2] = np.array([[2,0],[0,2]])

    oldLoss = Loss(X,k,pi,mu,sigma)
    J = []
    #主循环
    W = np.zeros((m,k))
    for step in range(0,iter):
        #求解W
        for i in range(0,m):
            total = 0
            for j in range(0,k):
                total += pi[j]*gaussian(X[i],mu[j],sigma[j])
            for j in range(0,k):
                W[i,j] = pi[j]*gaussian(X[i],mu[j],sigma[j]) / total

        #更新pi，mu,sigma
        newPi = np.zeros(k)
        newMu = np.zeros((k,n))
        newSigma = np.zeros((k,n,n))
        for j in range(0,k):
            tmpW = 0
            for i in range(1,m):
                tmpW += W[i,j]
                newMu[j] += W[i,j] * X[i]
                newSigma[j] += W[i,j] * np.array(np.mat(X[i] - mu[j]).T * np.mat(X[i] - mu[j]))
            newPi[j] = 1 / m * tmpW
            newMu[j] /= tmpW
            newSigma[j] /= tmpW

        #判断是否满足终止条件
        curLoss =  Loss(X,k,newPi,newMu,newSigma)
        if np.abs(oldLoss - curLoss) < 0.1:
            break
        else:
            print(oldLoss)

            J.append(oldLoss)
            oldLoss = curLoss
            pi = newPi
            mu = newMu
            sigma = newSigma
    plt.figure()
    plt.plot(J,'-*')
    plt.title('Loss Function')
    return pi,mu,sigma,W

if __name__ == '__main__':
    X = loadData()

    plt.figure()
    plt.plot(X[:,0],X[:,1],'*')
    plt.axis('equal')
    plt.title('original data')
    #运行EM算法
    k = 3
    [m,n] = np.shape(X)
    pi,mu,sigma,W = EM(X,k)

    clusters = dict()
    for i in range(0,k):
        clusters[i] = []

    for i in range(0,m):
        index = np.argmax(W[i])
        clusters[index].append(i)

    plt.figure()
    plt.plot(X[clusters[0],0], X[clusters[0],1],'*')
    plt.plot(X[clusters[1],0], X[clusters[1],1],'o')
    plt.plot(X[clusters[2],0], X[clusters[2],1],'d')
    plt.title('result')

在上述代码中，我们让 k=3 ，即由3个高斯模型组成混合模型。在求逆矩阵式，为了防止矩阵为奇异矩阵，我们使用 Σ+α∗E 代替 Σ 。$E$为单位矩阵。
原始数据的图形为

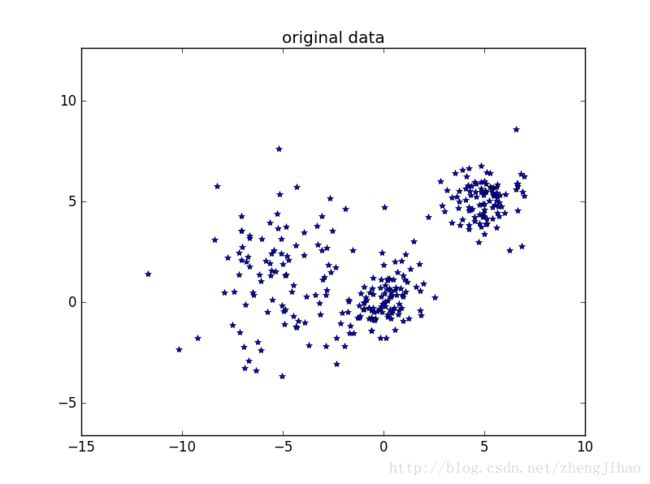
聚类结果为

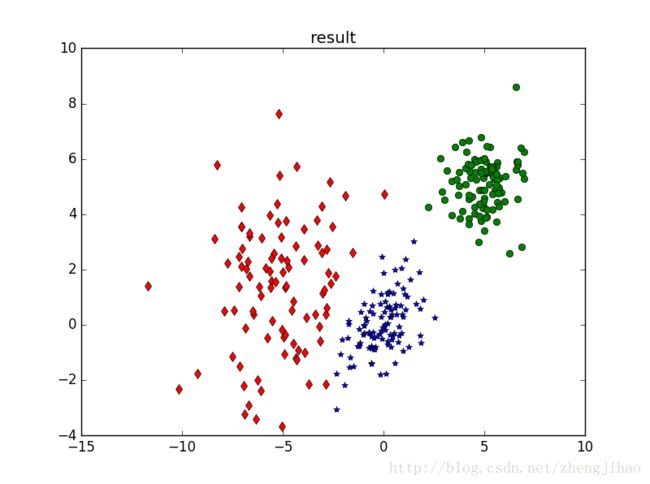
损失函数曲线为

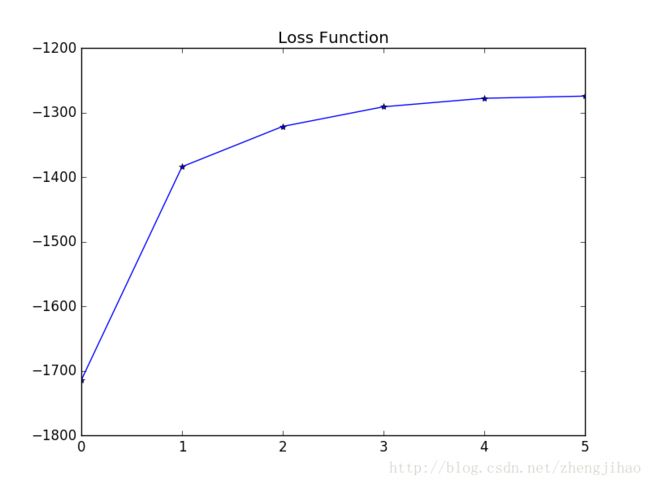
完整代码也可以在我的github中下载：
https://github.com/1092798448/EM-GMM.git
参考文献：
[1] 矩阵分析与应用 张贤达 著
[2] Andrew Ng 机器学习课件第7章 第8章