动态规划——背包问题(2)

多重背包的单调队列优化

例题

有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。
输入格式
第一行两个整数，N，V (0 接下来有 N 行，每行三个整数 vi,wi,si，用空格隔开，分别表示第 i 种物品的体积、价值和数量。
输出格式
输出一个整数，表示最大价值。
数据范围
0 0 0 提示
本题考查多重背包的单调队列优化方法。
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例：
10

思路

多重背包的原始状态转移方程
$f(i,j)=max(f(i-1,j),f(i-1,j-v)+w,\cdots ,f(i-1,j-sv)+sw)$此时s是满足$j-s\ast v>=0$的最大值
考虑用完全背包的优化方式来优化这个方程
$f(i,j-v)=max(f(i-1,j-v),f(i-1,j-2v)+w,\cdots ,f(i-1,j-(s+1)v)+(s)w)$这里的s为每样物品的最大个数。
此公式并不能推出f(i, j)
继续推导

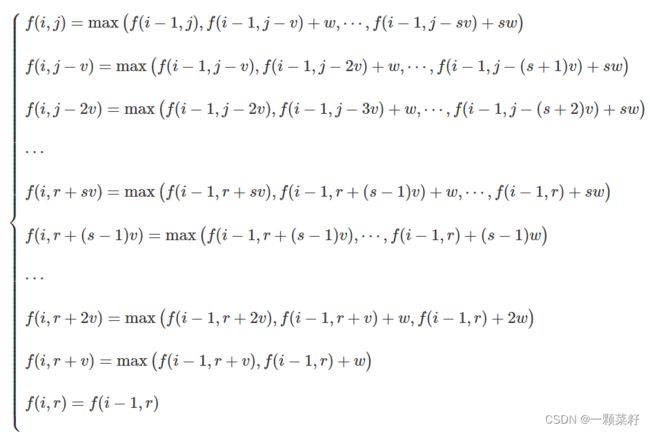
其中$r=jmod{v}_i$，也可以理解为 完全背包 下把当前物品 选到不能再选 后，剩下的 余数
得到 $f(i,r)=f(i-1,r)$ 后，我们再利用 完全背包优化思路 往回倒推一遍会惊奇的发现一个 滑动窗口求最大值的模型

	f(i, r)  =    f(i-1, r)
	f(i, r + v) = max(f(i - 1, r + v) - w, f(i - 1, r)) + w
	f(i, r + 2 * v) = max(f(i - 1, r + 2 * v) - 2 * w, f(i - 1, r + v)) - w, f(i - 1, r)) + 2 * w
	...
	f(i, j) = max(f(i - 1, j) - s * w, f(i - 1, j - v) - (s - 1) * w, ... ， f(i - 1, j - sv)) + s * w

可以发现每次只需要获得至多窗口值小于等于s的上一层的最大值即可

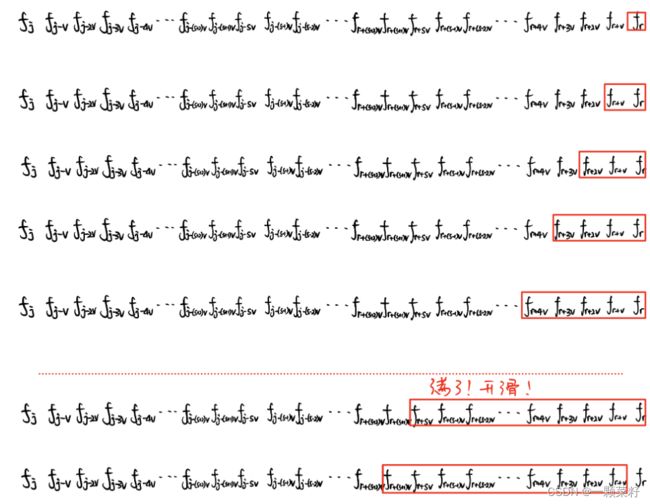
代码

N = 20010
q, f, g = [0] * N, [0] * N, [0] * N

n, m = map(int, input().split())

for i in range(n) :
	v, w, s = map(int, input().split())
	g = f[:]
	for j in range(v) :
		hh, tt = 0, -1
		for k in range(j, m + 1, v) :
			if hh <= tt and q[hh] < k - s * v :
				hh += 1
			while hh <= tt and g[q[tt]] - (q[tt] - j) // v * w <= g[k] - (k - j) // v * w :
				tt -= 1
			tt += 1
			q[tt] = k
			f[k] = g[q[hh]] + (k - q[hh]) // v * w
print(f[m])

二维费用背包问题

例题

有 N 件物品和一个容量是 V 的背包，背包能承受的最大重量是 M。

每件物品只能用一次。体积是 vi，重量是 mi，价值是 wi。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

输入格式
第一行三个整数，N,V,M，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。

接下来有 N 行，每行三个整数 vi,mi,wi，用空格隔开，分别表示第 i 件物品的体积、重量和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0 0 0 0 输入样例
4 5 6
1 2 3
2 4 4
3 4 5
4 5 6
输出样例：
8

N = 110
f = [[0] * N for _ in range(N)]

n, V, M = map(int, input().split())
for i in range(n) :
	v, m, w = map(int, input().split())
	for j in range(V, v - 1, -1):
		for k in range(M, m - 1, -1) :
			f[j][k] = max(f[j][k], f[j - v][k - m] + w)
print(f[V][M]) 

背包问题装法的总结：至多、恰好、至少

背包最多装V体积

状态表示f[i, j]：前i个物品中选择体积不大于j的选法
初始化：当一个物品都没选时，f[0, j] = 0
循环体积时，当vi>j时，这个物品是不能选的，所以范围是[vi, V]

背包恰好装V体积

状态表示f[i, j]：前i个物品中选择体积恰好为j的选法
初始化：当一个物品都没选时，只有f[0, 0]是有意义的为0，其它的没有意义（f[0, j], j!=0）相应的初始化为INF
循环体积时，当vi>j时，这个物品是不能选的，所以范围是[vi, V]

背包最少装V体积

状态表示f[i, j]：前i个物品中选择体积至少为j的选法
初始化：当一个物品没选时，只有f[0, 0]是有意义的为0，其它的没有意义（f[0, j], j!=0）相应的初始化为INF
循环体积时，当vi>j时，这个物品是可以选的，所以范围是[0, V]，可以特判if vi > j : f[i, j] = max(f[i - 1, j], wi)，也可以做统一化处理if v > j : f[i, j] = max(f[i - 1, j],f[i -1, max(0, j - vi)] + wi)

例题

潜水员为了潜水要使用特殊的装备。

他有一个带2种气体的气缸：一个为氧气，一个为氮气。

让潜水员下潜的深度需要各种数量的氧和氮。

潜水员有一定数量的气缸。

每个气缸都有重量和气体容量。

潜水员为了完成他的工作需要特定数量的氧和氮。

他完成工作所需气缸的总重的最低限度的是多少？

例如：潜水员有5个气缸。每行三个数字为：氧，氮的（升）量和气缸的重量：

3 36 120

10 25 129

5 50 250

1 45 130

4 20 119
如果潜水员需要5升的氧和60升的氮则总重最小为249（1，2或者4，5号气缸）。

你的任务就是计算潜水员为了完成他的工作需要的气缸的重量的最低值。

输入格式
第一行有2个整数 m，n。它们表示氧，氮各自需要的量。

第二行为整数 k 表示气缸的个数。

此后的 k 行，每行包括ai，bi，ci，3个整数。这些各自是：第 i 个气缸里的氧和氮的容量及气缸重量。

输出格式
仅一行包含一个整数，为潜水员完成工作所需的气缸的重量总和的最低值。

数据范围
1≤m≤21,
1≤n≤79,
1≤k≤1000,
1≤ai≤21,
1≤bi≤79,
1≤ci≤800
输入样例：
5 60
5
3 36 120
10 25 129
5 50 250
1 45 130
4 20 119
输出样例：
249

M, N = 22, 80
INF = int(1e9)

f = [[INF] * N for _ in range(N)]
f[0][0] = 0
m, n = map(int, input().split())

K = int(input())
for k in range(K) :
	a, b, c = map(int, input().split())
	for i in range(m, -1, -1) :
		for j in range(n, -1, -1) :
			f[i][j] = min(f[i][j], f[max(i - a, 0)][max(j - b, 0)] + c) 
print(f[m][n])

求解方案数

初始化和循环顺序

状态表示f[i, j]:表示前i个物品选取体积满足至多/恰好/至少为j的方案数

初始化：f[0, 0] = 1满足状态表示意义，当j!=0时f[0, j]，在体积至多为j时，方案数为1，即f[0, j] = 1。恰好为j时，方案数为0，即f[0, j] = 0。在体积至少为j时，方案数为i即f[0, j] = 0。

组合数：先循环物品再循环体积
排列数，先循环体积在循环物品
状态转移方程：
0-1背包f[i, j] += f[i - 1, j - vi]
完全背包f[i, j] += f[i, j - vi]
多重背包f[i, j] += f[i, j - vi * k]

例题

给定 N 个正整数 A1,A2,…,AN，从中选出若干个数，使它们的和为 M，求有多少种选择方案。

输入格式
第一行包含两个整数 N 和 M。

第二行包含 N 个整数，表示 A1,A2,…,AN。

输出格式
包含一个整数，表示可选方案数。

数据范围
1≤N≤100,
1≤M≤10000,
1≤Ai≤1000,
答案保证在 int 范围内。

输入样例：
4 4
1 1 2 2
输出样例：
3

N = 10010
f = [0] * N

n, m = map(int, input().split())

nums = list(map(int, input().split()))
f[0] = 1
for i in range(n) :
    for j in range(m, nums[i] - 1, -1) :
        f[j] += f[j - nums[i]]
        
print(f[m])

小明手里有n元钱全部用来买书，书的价格为10元，20元，50元，100元。

问小明有多少种买书方案？（每种书可购买多本）

输入格式
一个整数 n，代表总共钱数。

输出格式
一个整数，代表选择方案种数。

数据范围
0≤n≤1000
输入样例1：
20
输出样例1：
2
输入样例2：
15
输出样例2：
0
输入样例3：
0
输出样例3：
1

N = 1010
f = [0] * N

money = [10, 20, 50, 100]

m = int(input())

f[0] = 1
for v in money :
    for j in range(v, m + 1) :
        f[j] += f[j - v]
        
print(f[m])
    

求解具体方案

思路

f[i, j] = max(f[i - 1, j], f[i - 1, j - v] + w)，f[i, j]只能由以上两个状态中得出。
分为三种情况：

考虑方案按字典顺序输出

例题

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出 字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是 1…N。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一行，包含若干个用空格隔开的整数，表示最优解中所选物品的编号序列，且该编号序列的字典序最小。

物品编号范围是 1…N。

数据范围
0 0 输入样例
4 5
1 2
2 4
3 4
4 6
输出样例：
1 4

N = 1010
f = [[0] * N for _ in range(N)]
v, w = [0] * N, [0] * N

n, m = map(int, input().split())
for i in range(1, n + 1) :
	v[i], w[i] = map(int, input().split())

for i in range(n, 0, -1) :
	for j in range(m + 1) :
		f[i][j] = f[i + 1][j]
		if j >= v[i] :
			f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i])

j = m
for i in range(1, n + 1) :
	if j >= v[i] and f[i][j] == f[i + 1][j - v[i]] + w[i] :
		print(i, end = " ")
		j -= v[i]

总结

到此为止，背包问题第二部分就讲完了，涉及到了多重背包单调队列优化、不同背包问法的背包初始化和循环顺序问题、以及求方案数和具体方案的过程
求具体方案时背包不能使用滚动数组
在不使用滚动数组的情况下，0-1背包和分组背包要特写不选物品的情况即f[i, j] = f[i - 1, j]，其他背包则包含在物品选取个数的逻辑中。