rvo动态避障算法源码分析

rvo动态避障算法

源码: snape (Jamie Snape) · GitHub

文档: RVO2 Library - Reciprocal Collision Avoidance for Real-Time Multi-Agent Simulation

网友翻译的中文版文档:  导航动态避让算法RVO的优化ORCA(Optimal Reciprocal Collision Avoidance)_u012740992的专栏-CSDN博客_orca算法

本文就rvo中动态避障的算法源码做一个简单分析

代码取自:https://github.com/warmtrue/RVO2-Unity 大约是2021-8-10这个时间取的,

是一个例子, 将rvo整合到unity里

rvo详可见上文链接

这里做一个简单的说明

RVO算法简要说明

运动的物体A与物体B,假设物体A的位置为坐标原点,并将A变成质点,

则B相应的半径增大,新的圆B记录CircleNew

如下图示,以原点为顶点,原点到CircleNew做切线,组成一个锥形区域(图中划横线的)

计算A,B之间的相对速度Va,如果Va位于锥形区域以外,则A B将不会发生碰撞,反之,则会在未来某个时间发生碰撞

进一步计算,假设时间取为t,

物体A的半径记为rA, B的半径记录rB, 位置分别为PA ,PB

CircleNew圆记位于PB - PA 半径为rA + rB,

对整个坐标系进行缩放1/t,这样速度的单位就变成秒

原来的大圆,就缩放为圆心 (PB-PA)/t 半径为(rA+rB)/t,这个新圆被称为截止圆cutoff-circle

可以看出速度的选择范围如以下右图所示,除了灰色圆头锥型区域以外,白色区域都是可选的相对速度Vr=Va-Vb(Va Vb分别为A,B的速度)方向以及大小.如图中的蓝色速度与红色速度

如果Vr速度位于灰色的锥型区,就需要调整速度至空白区域,即给速度加个分量

如下图的蓝色小箭头,这种情况下的相对速度,就需要往旁边调整,锥形区域中的切边,被称为leg

根据速度的方向大小,也有可能往cutoff-circle处调整或另一条leg处调整

如下图,往cutoff-circle处调整相对速度Vr,

这个调整的速度分量我们称之为u,

物体A调整后的速度为 Va-new = Va + u,

令A和B各负责一半的速度调整,则Va-new = Va + 0.5 *u

这样即可保证A B在t时间内不会碰撞

选取了u为调整分量后,可以发现,Va-new的取值是一个半平面,

这个半平面的分割线是以垂直向量u为方向,过点Va+0.5*u的直线,在此处称之为line

在这个半平面的一侧速度都可以为备选速度

如果有多个物体都在做避障处理,就会得到一系列的半平面,这些半平面的交集,就是速度的可选范围

如下图中划斜线的区域

在斜线区域的边缘,取则一个速度,并使这个速度的长度,尽量接近程序中预设物体A的最大速率(Vopt的长度),即可

在选速度时,尽量保证新的速度与Vopt方向相同,长度相同,如果不能保证方向相同,则尽量保证长度不大于Vopt(即舍弃方向与Vopt相同这个约束)

观察RVO代码实现,line取过点Va+0.5*u,保证了交集是一定存在的

可以认为所有的line都以为点0.5*u(每个line的u取值不同),那么所有的line的交集是包含原点的凸多边形

再将整个坐标系做一个平移到Va,所得的交集是一个包含点Va的凸多边形

隐含的假设是其它寻路物体的下一个时刻速度为零,避免程序出现没有交集而无法选取速度的情况,如下,,在每个速度半平面没有交点的情况下(中间那张图),选择让对方的速度为0,从而得到一个交集(最右边的那张图)

RVO认为B C也会做同样的处理,从而达到障碍的目的

致此,RVO算法简要说明结束-------------

RVO动态避障代码分析

动态功能代码主要在这个函数:computeNewVelocity

红框处这个循环,就是处理动态障碍开始

1 计算相对速度,相对位置

代码:

   

 combineRadius就是把A看到质点后,B物体半径相对扩大    

  

2 计算速度调整

代码截图

分析:

2.1 代码中变量对应的几何意义

2.2 dotProduct1

判断是否往cutoff-circle调整的代码:

if (dotProduct1 < 0.0f && RVOMath.sqr(dotProduct1) > combinedRadiusSq * wLengthSq)

w与relativePosition夹角记做

值为 length(w) * length(relativePosition) * cos()

此值小零就意味着可能需要往cutoff-circle处调整相对速度

RVOMath.sqr(dotProduct1) > combinedRadiusSq * wLengthSq

条件中的另一个,将不等式两边的wLengthSq去掉,

很明显实际上比较是cos()的平方与cos<角1>的平方,

如果此条件也满足,说明一定是在cutoff-circle上调整速度了

2.3 计算cutoff-circle的u

这个比较简单,知道判断规则,其实就是cutoff-circle圆心与relativeVelocity连线,即w

取w的方向 line.direction自然就要取与w垂直(即对应切线方向)

u的长度要用cutoff-circle的半径减去w的长度wLength

如此就得到了往cutoff-circle调整时,向量u以及对应的半平面分割线的方向

2.4 往leg处调整

leg就是原点与cutoff-circle做的切线

如下图,当速度为红色所示向量时,要按蓝色箭头的方向调整

利用叉积(sin值)判断是位于哪条leg,代码:

RVOMath.det(relativePosition, w)

构造二元一次方程组,求向调整向量u

Rx,Ry为cutoff-circle圆心坐标 leg假设为(x,y)单位向量,则与leg垂直的u为(y,-x)

cutoff-circle的圆心坐标分别在u与leg上投影

方程组如下:

Rx * x + Ry * y = leg  leg是圆C_cutoff的切点到A点的长度,用勾股定理就可以求得

Rx * y - Ry * x = Rad/t

代码:

/* Project on left leg. */

line.direction = new Vector2(relativePosition.x() * leg - relativePosition.y() * combinedRadius, relativePosition.x() * combinedRadius + relativePosition.y() * leg) / distSq;

解此方程组,就可以求得(x,y) leg的单位向量,再根据leg,求得u

代码:

float dotProduct2 = relativeVelocity * line.direction;

u = dotProduct2 * line.direction - relativeVelocity;

另外还有物体A与物体B已经发生碰撞的情况,看代码处理类似向cutoff-circle调整,此处不特别分析了

3 linearProgramX

对应linearProgram1 linearProgram2 linearProgram3 这三个函数

有了速度备选集合后,要选一个速度newVelocity_,它的方向与长度,应尽量与prefVelocity_相近似,或者完全相同

对所有的动态物体进行处理后,会得到一系列的半平面,

它们的分割线记录在Agent.orcaLines_里面

根据之前的说明,可以很容易推断出,这些line的交集是一个以velocity_为”中心点”的凸多边形

即所有的分割线,都以各自的u方向以及u的长度,相对velocity_拉开

并且,根据代码迭代来看,velocity_初始值是0,之后它的长度一般是不会大于prefVelocity_的

(除非程序有动态改变prefVelocity_的需求)

3.1 linearProgram2

将prefVelocity设置迭代的初始速度 result

判断循环判断result是否在orcaLines_所划分的半平面内

利用result到分割线的距离正负值来判断,从代码推断,在分割线的左边表示在半平面内

代码如下:

if (RVOMath.det(lines[i].direction, lines[i].point - result) > 0.0f)

如果距离为正,说明在半平面外,调用linearProgram1算出来的最接近的速度

3.2 linearProgram1

此函数直观表示如下:

velocity_是当前的速度,它必然在orcaLines_交集组成的凸多边形当中

prefVelocity_可能不在交集中,linearProgram1负责在凸多边形的一条边上,找出最合适的速度例如上图中的newVelocity_

prefVelocity_够不能交集所在区域的情况(这种情况应该是动态改了prefVelocity_)

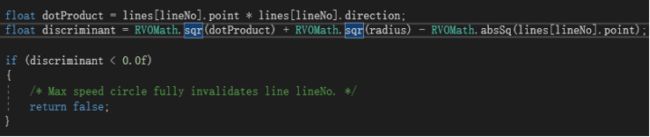
根据勾股定理判断,dotProduct是一条直角边的长, RVOMash.absSq(lines[lineNo].port)是斜边,将它们与速度的长radius比较,代码如下:

之后,计算以原点为圆心以,以prefVelocity_的长为半径的圆与当前line分割线的两个交点tLeft tRight,

计算让交集凸多边形的其它边与当前line的交点,判断交点是否位于tLeft 与tRight之间,如果是根据情况替换tLeft或tRight

实际上就是prefVelocity_旋转,与当前交集多边形line相交,如果交点在边的两个端点内,就取交点,

如果不是,判断边的端点是否在交点内,即取两个线段的交集

如果两个线段没有交集,也被判断为失败

各个变量的几何意义如下:

tLeft tRight的初始值如上图所示,图中红色lines[lineNo].point表示该点的长度

重线的长度为 length(lines[lineNo].point) - RVOMath.sqr(dotProduc)

如下二图所示,

原点到交集边的垂足P  tLeft tRight实际上是当前line上的点到垂足的长度比例,因为不断迭代,tLeft tRight会变化(变小)

紫色即为选取的速度:

取边的两个端点间的某一个点,此时速度方向变了,但速度大小与prefVelocity_一致

取边的端点,此时速度方向变了,速度大小也比prefVelocity_小

RVO代码很处理比较复杂,还是配合linearProgram3处理,实际上就是完成上面这个步骤,

在速度交集多边形上的边上选一个点

再来看linearProgram1的迭代tLeft 与tRight的代码,

 循环每条line,与当前处理的line(以下简称为line_cur)求它们的”交点”t(t其实是一个比例)

为交点到line.point距离

注意这三行代码:

float denominator = RVOMath.det(lines[lineNo].direction, lines[i].direction);

float numerator = RVOMath.det(lines[i].direction, lines[lineNo].point - lines[i].point);

float t = numerator / denominator;

其实是在求两条直线的交点,lines[lineNo].point - lines[i].point隐含了坐标平移

Lines[lineNo]的直线方程就会变成  y=ax

而lines[i]的直线方程在新坐标系中会变成 (y-py)=b(x-px) 其中(px,py)就是lines[lineNo].point - lines[i].point,

为坐标平移后的点

由于t是一个距离点lines[lineNo.point]的比例,所以平移不影响计算结果.

相应的推导过程比较简单,二元一次方程组求解,即可得到

t = numerator / denominator

t是交点到lines[lineNo.point]的距离

根据denominator的值判断t是替换tLeft,还是tRight

过程不太好理解,但原理其实非常简单

最后这段代码,就是在迭代完成之后选取result了,比较简单,没啥好说的

3.3 linearProgram3

如果linearProgram2中有出现失败的现象(tLeft > tRight,或者速度太小够不到交集所在的区域)

会导致linearProgram3的处理

其实笔者认为,直接以原点为圆心,prefVelocity_为半径划个圆,

将速度交集多边形所有的顶点判断是否在圆中,

然后对在圆中的顶点的边进行速度处理,也可以,不知道算法为什么不这么写.

算法是对出现失败前的line进行处理,求出它们与当前line的交点,并重新设置它们的方向

line.direction = RVOMath.normalize(lines[j].direction - lines[i].direction);

代码如下:

红框处是这个算法不太好理解的部分,为什么要这样重新设定半平面的方向

原因1 这样设定会导致交集一定比原来的小(即保证速度的合法性)

原因2 这样设定会让新的速度选择尽量出现在当前的line上

(和之后调用linearProgram2的速度取值有关)

这两点笔者反复思考过,应该就是这段代码的真实意图,可以用图来直观的理解

新的line的方向其实是夹角的角平分线,可以看出,交集会变小

if (linearProgram2(projLines, radius, new Vector2(-lines[i].direction.y(), lines[i].direction.x()), true, ref result) < projLines.Count)

这行代码再次调用linearProgram2计算新的速度,起始的速度方向变成与当前处理的line重直,

这就是上文提到的原因2,所有半平面分割线方向调整,都是为了保证新的速度尽量落在当前处理的line上

最后说明一下求交点的代码:

line.point = lines[i].point + (RVOMath.det(lines[j].direction, lines[i].point - lines[j].point) / determinant) * lines[i].direction;

这里

将(RVOMath.det(lines[j].direction, lines[i].point - lines[j].point)记做dis_ij

将(RVOMath.det(lines[j].direction, lines[i].point - lines[j].point) / determinant)记录hypotenuse_len 它表示line[i].Point到交点的距离,即另一个直角三角形的斜边

这些变量的几何意义如下图:

这样,就可以利用lines[i].point + hypotenuse_len * lines[i].direction直线算出交点了,

致此RVO动态避障代码分析完毕

作者:林绍川