信用评分卡模型

https://www.cnblogs.com/dzy1995/p/10556226.html

https://zhuanlan.zhihu.com/p/44663658

https://blog.csdn.net/htbeker/article/details/79697557

https://zhuanlan.zhihu.com/p/56738542

什么是评分卡？

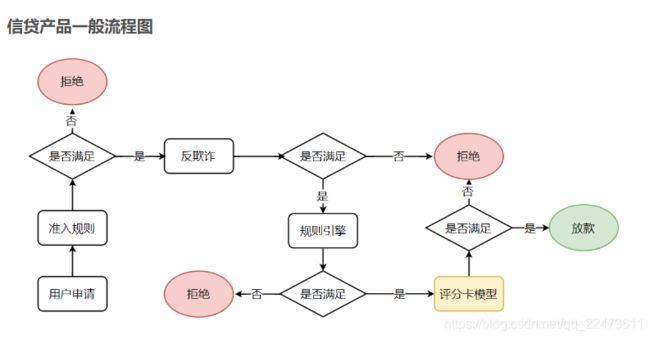
信贷场景中的评分卡

• 以分数的形式来衡量风险几率的一种手段
• 是对未来一段时间内违约/逾期/失联概率的预测
• 有一个明确的区间，不一定是正区间，不过业界都习惯用正区间
• 通常分数越高越安全
• 数据驱动（之前往往是专家驱动，但是专家也有考虑不到或者考虑不全的情况）
• 评分卡类别：反欺诈评分卡、申请评分卡、行为评分卡、催收评分卡 

申请评分卡的概念

用在申请环节，以申请者在申请当日及过去的信息为基础，预测未来放款后的逾期或者违约概率

 为什么要开发申请评分卡？？

• 风险控制：借贷生命周期的第一个关口
• 营销：优质客户识别
• 资本管理：可作为PD模型的一个因子

评分卡的特性

• 稳定性

当总体逾期/违约概率不变时，分数的分布也应不变

• 区分性

违约人群与正常人群的分数应当有显著差异

• 预测能力

低分人群的违约率更高

• 和逾期概率等价

评分可以精准地反映违约/逾期概率，反之亦然

本次建模基本流程：

1.数据准备：收集并整合在库客户的数据，定义目标变量，排除特定样本。
2.探索性数据分析：评估每个变量的值分布情况，处理异常值和缺失值。
3.数据预处理：变量筛选，变量分箱，WOE转换、分割训练集测试集。
4.模型开发：逻辑回归拟合模型。
5.模型评估：常见几种评估方法，ROC、KS等。
6.生成评分卡

 

申请评分卡常用的特征

• 个人信息 学历 性别 收入
• 负债信息 在本金融机构或者其他金融机构负债情况
• 消费能力 商品购买纪录，出境游，奢侈品消费
• 历史信用记录 历史逾期行为
• 新兴数据 人际社交 网络足迹 出行 个人财务

1.3定义目标变量

申请者评分模型需要解决的问题是未来一段时间（如12个月）客户出现违约（如至少一次90天或90天以上逾期）的概率。在这里“12个月”为“观察时间窗口”，“至少一次90天或90天以上逾期”为表现时间窗口即违约日期时长，那么我们如何确定观察时间窗口和违约日期时长（如M2算违约，还是M3算违约）呢？可定义表现期内出现M3一次及以上、M2两次及以上为坏客户，

建立模型预测客户在未来一段时间内是否会违约，那必然需要先定义违约，逾期多长时间算违约，不同业务标准不同。与数据集中还款表现loan_status字段相关，作为目标变量，剩下的字段则作为解释变量

 

基于Python的信用评分卡模型分析 https://www.jianshu.com/p/f931a4df202c

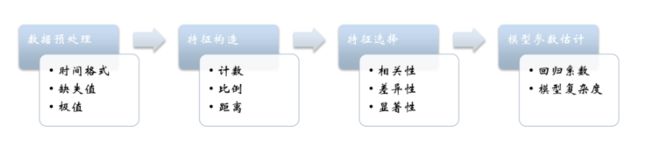
一、项目流程，本次建模基本流程：

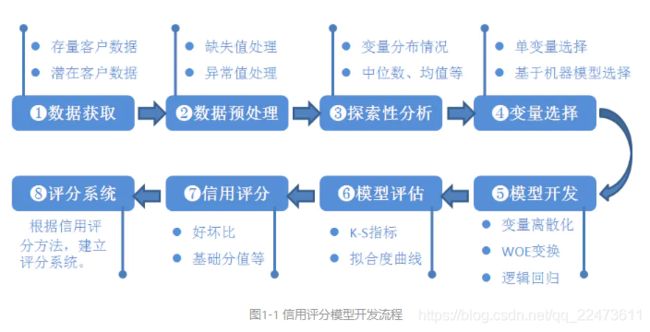
信用风险评级模型的主要开发流程如下：
（1） 数据获取，包括获取存量客户及潜在客户的数据。存量客户是指已经在证券公司开展相关融资类业务的客户，包括个人客户和机构客户；潜在客户是指未来拟在证券公司开展相关融资类业务的客户，主要包括机构客户，这也是解决证券业样本较少的常用方法，这些潜在机构客户包括上市公司、公开发行债券的发债主体、新三板上市公司、区域股权交易中心挂牌公司、非标融资机构等。
（2） 数据预处理，主要工作包括数据清洗、缺失值处理、异常值处理，主要是为了将获取的原始数据转化为可用作模型开发的格式化数据。
（3） 探索性数据分析，该步骤主要是获取样本总体的大概情况，描述样本总体情况的指标主要有直方图、箱形图等。
（4） 变量选择，该步骤主要是通过统计学的方法，筛选出对违约状态影响最显著的指标。主要有单变量特征选择方法和基于机器学习模型的方法 。
（5） 模型开发，该步骤主要包括变量分段、变量的WOE（证据权重）变换和逻辑回归估算三部分。
（6） 模型评估，该步骤主要是评估模型的区分能力、预测能力、稳定性，并形成模型评估报告，得出模型是否可以使用的结论。常见几种评估方法，ROC、KS等。
（7） 信用评分，根据逻辑回归的系数和WOE等确定信用评分的方法。将Logistic模型转换为标准评分的形式。
（8） 建立评分系统，根据信用评分方法，建立自动信用评分系统。

 

二、数据获取

数据的获取途径主要有两个：

• 金融机构自身字段：例用户的年龄，户籍，性别，收入，负债比，在本机构的借款和还款行为等；
• 第三方机构的数据：如用户在其他机构的借贷行为，用户的消费行为数据等。

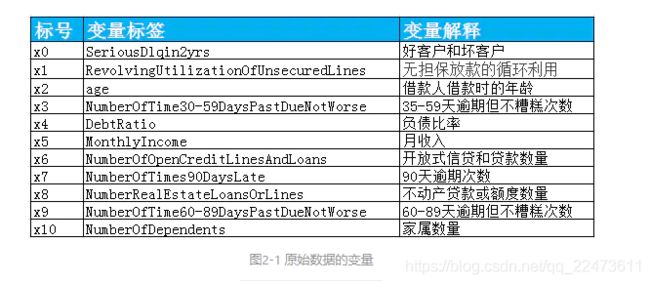
数据属于个人消费类贷款，只考虑信用评分最终实施时能够使用到的数据应从如下一些方面获取数据：
– 基本属性：包括了借款人当时的年龄。
– 偿债能力：包括了借款人的月收入、负债比率。
– 信用往来：两年内35-59天逾期次数、两年内60-89天逾期次数、两年内90天或高于90天逾期的次数。
– 财产状况：包括了开放式信贷和贷款数量、不动产贷款或额度数量。
– 贷款属性：暂无。
– 其他因素：包括了借款人的家属数量（不包括本人在内）。
– 时间窗口：自变量的观察窗口为过去两年，因变量表现窗口为未来两年。

 

三、数据预处理 

数据预处理主要包括数据清洗，变量分箱和 WOE 编码三个步骤。

数据清洗主要是对原始数据中脏数据，缺失值，异常值进行处理。关于对缺失值和异常值的处理，我们采用的方法非常简单粗暴，即删除缺失率超过某一阈值（阈值自行设定，可以为50%，90%等）的变量，将剩余变量中的缺失值和异常值作为一种状态 。

在对数据处理之前，需要对数据的缺失值和异常值情况进行了解。Python内有describe()函数，可以了解数据集的缺失值、均值和中位数等。

    #载入数据
    data = pd.read_csv('cs-training.csv')
    #数据集确实和分布情况
    data.describe().to_csv('DataDescribe.csv')

数据集的详细情况：

图3-1 变量详细情况

从上图可知，变量MonthlyIncome和NumberOfDependents存在缺失，变量MonthlyIncome共有缺失值29731个，NumberOfDependents有3924个缺失值。

3.1 缺失值处理

这种情况在现实问题中非常普遍，这会导致一些不能处理缺失值的分析方法无法应用，因此，在信用风险评级模型开发的第一步我们就要进行缺失值处理。缺失值处理的方法，包括如下几种。
（1） 直接删除含有缺失值的样本。
（2） 根据样本之间的相似性填补缺失值。
（3） 根据变量之间的相关关系填补缺失值。
变量MonthlyIncome缺失率比较大，所以我们根据变量之间的相关关系填补缺失值，我们采用随机森林法：

# 用随机森林对缺失值预测填充函数
def set_missing(df):
    # 把已有的数值型特征取出来
    process_df = df.ix[:,[5,0,1,2,3,4,6,7,8,9]]
    # 分成已知该特征和未知该特征两部分
    known = process_df[process_df.MonthlyIncome.notnull()].as_matrix()
    unknown = process_df[process_df.MonthlyIncome.isnull()].as_matrix()
    # X为特征属性值
    X = known[:, 1:]
    # y为结果标签值
    y = known[:, 0]
    # fit到RandomForestRegressor之中
    rfr = RandomForestRegressor(random_state=0, 
    n_estimators=200,max_depth=3,n_jobs=-1)
    rfr.fit(X,y)
    # 用得到的模型进行未知特征值预测
    predicted = rfr.predict(unknown[:, 1:]).round(0)
    print(predicted)
    # 用得到的预测结果填补原缺失数据
    df.loc[(df.MonthlyIncome.isnull()), 'MonthlyIncome'] = predicted
    return df

NumberOfDependents变量缺失值比较少，直接删除，对总体模型不会造成太大影响。对缺失值处理完之后，删除重复项。

    data=set_missing(data)#用随机森林填补比较多的缺失值
    data=data.dropna()#删除比较少的缺失值
    data = data.drop_duplicates()#删除重复项
    data.to_csv('MissingData.csv',index=False)

3.2 异常值处理

缺失值处理完毕后，我们还需要进行异常值处理。异常值是指明显偏离大多数抽样数据的数值，比如个人客户的年龄为0时，通常认为该值为异常值。找出样本总体中的异常值，通常采用离群值检测的方法。
首先，我们发现变量age中存在0，显然是异常值，直接剔除：

    # 年龄等于0的异常值进行剔除
    data = data[data['age'] > 0]

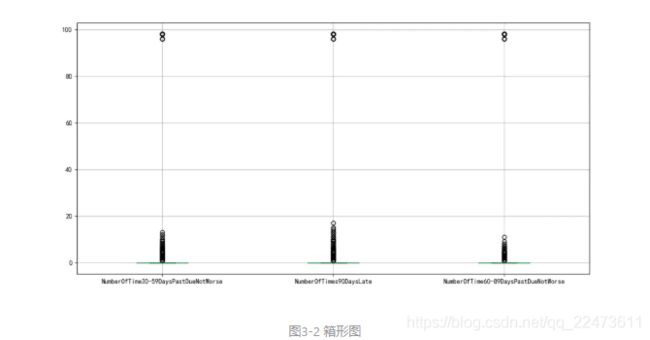
对于变量NumberOfTime30-59DaysPastDueNotWorse、NumberOfTimes90DaysLate、NumberOfTime60-89DaysPastDueNotWorse这三个变量，由下面的箱线图图3-2可以看出，均存在异常值，且由unique函数可以得知均存在96、98两个异常值，因此予以剔除。同时会发现剔除其中一个变量的96、98值，其他变量的96、98两个值也会相应被剔除。

图3-2 箱形图

 

剔除变量NumberOfTime30-59DaysPastDueNotWorse、NumberOfTimes90DaysLate、NumberOfTime60-89DaysPastDueNotWorse的异常值。另外，数据集中好客户为0，违约客户为1，考虑到正常的理解，能正常履约并支付利息的客户为1，所以我们将其取反。

 

    #剔除异常值
    data = data[data['NumberOfTime30-59DaysPastDueNotWorse'] < 90]
    #变量SeriousDlqin2yrs取反
    data['SeriousDlqin2yrs']=1-data['SeriousDlqin2yrs']

3.3 数据切分

为了验证模型的拟合效果，我们需要对数据集进行切分，分成训练集和测试集。

from sklearn.cross_validation import train_test_split

    Y = data['SeriousDlqin2yrs']
    X = data.ix[:, 1:]
    #测试集占比30%
    X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)
    # print(Y_train)
    train = pd.concat([Y_train, X_train], axis=1)
    test = pd.concat([Y_test, X_test], axis=1)
    clasTest = test.groupby('SeriousDlqin2yrs')['SeriousDlqin2yrs'].count()
    train.to_csv('TrainData.csv',index=False)
    test.to_csv('TestData.csv',index=False)

四、探索性分析（EDA）

在建立模型之前，我们一般会对现有的数据进行 探索性数据分析（Exploratory Data Analysis） 。 EDA是指对已有的数据(特别是调查或观察得来的原始数据)在尽量少的先验假定下进行探索。常用的探索性数据分析方法有：直方图、散点图和箱线图等。
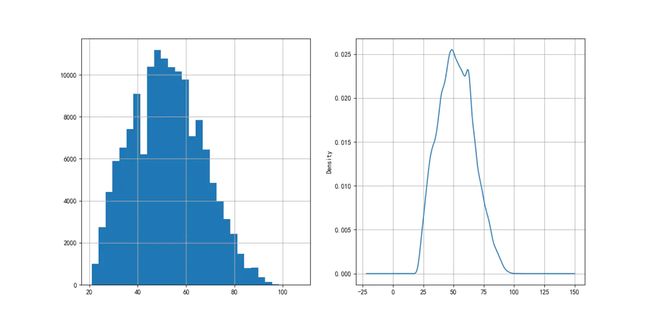
客户年龄分布如图4-1所示，可以看到年龄变量大致呈正态分布，符合统计分析的假设。

2 EDA（探索性数据分析）

该步骤主要是获取数据的大概情况，例如每个字段的缺失值情况（缺失值补全）、异常值情况（删除缺失率70%以上的变量）、平均值、中位数、最大值、最小值、分布情况等。以便制定合理的数据预处理方案。

特征衍生是现有的特征进行某种组合,生成新的具有含义的特征

经过一系列特征初筛和特征衍生，变量已经从144个降低至82个

图4-1 客户年龄分布

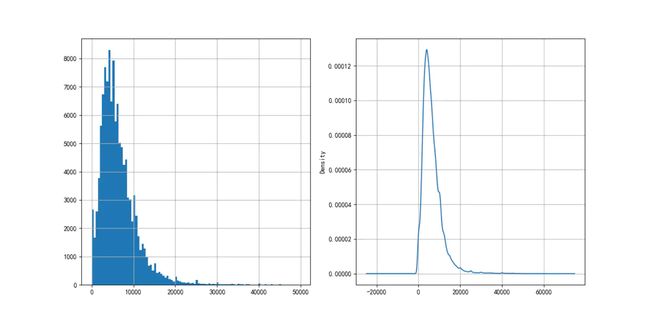
客户年收入分布如图4-2所示，月收入也大致呈正态分布，符合统计分析的需要。

图4-2 客户收入分布

五、变量选择 ，特征变量选择

特征变量选择(排序)对于数据分析、机器学习从业者来说非常重要。好的特征选择能够提升模型的性能，更能帮助我们理解数据的特点、底层结构，这对进一步改善模型、算法都有着重要作用。至于Python的变量选择代码实现可以参考结合Scikit-learn介绍几种常用的特征选择方法。
在本文中，我们采用信用评分模型的变量选择方法，通过WOE分析方法，即是通过比较指标分箱和对应分箱的违约概率来确定指标是否符合经济意义。首先我们对变量进行离散化（分箱）处理。

特征的分箱

分箱简单的解释是：分箱就是为了做到同组之间的差异尽可能的小，不同组之间的差异尽可能的大。

分箱的定义：

• 将连续变量离散化
• 将多状态的离散变量

特征分箱的优势：

1. 特征分箱可以有效处理特征中的缺失值和异常值。
2. 特征分箱后，数据和模型会更稳定。
3. 特征分箱可以简化逻辑回归模型，降低模型过拟合的风险，提高模型的泛化能力。
4. 将所有特征统一变换为类别型变量。
5. 分箱后变量才可以使用标准的评分卡格式，即对不同的分段进行评分。

分箱方法：https://www.jianshu.com/p/c3fa53c54cca

A. 无监督：(1) 等宽 (2) 等频 (3) 聚类（k-means）

B. 有监督：(1) 卡方分箱法(ChiMerge) (2) ID3、C4.5、CART等单变量决策树算法 (3)  信用评分建模的IV最大化分箱 、(4)  best-ks分箱法等 

5.1 分箱处理

变量分箱（binning）是对连续变量离散化（discretization）的一种称呼。信用评分卡开发中一般有常用的等距分段、等深分段、最优分段。其中等距分段（Equval length intervals）是指分段的区间是一致的，比如年龄以十年作为一个分段；等深分段（Equal frequency intervals）是先确定分段数量，然后令每个分段中数据数量大致相等；最优分段（Optimal Binning）又叫监督离散化（supervised discretizaion），使用递归划分（Recursive Partitioning）将连续变量分为分段，背后是一种基于条件推断查找较佳分组的算法。
我们首先选择对连续变量进行最优分段，在连续变量的分布不满足最优分段的要求时，再考虑对连续变量进行等距分段。最优分箱的代码如下：

# 定义自动分箱函数---最优分箱
def mono_bin(Y, X, n ):
    r = 0  #设定斯皮尔曼 初始值
    good=Y.sum()   #好客户的人数
    bad=Y.count()-good   #坏客户的人数
  #下面这段就是分箱的核心 ，就是 机器来 选择 指定 最优的分箱节点，代替我们自己来设置
    while np.abs(r) < 1:   #while ,不满足条件时，跳出循环
        d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.qcut(X, n)}) #注意这里是pd.qcut, Bucket： 将 X 分为 n 段，n由 斯皮尔曼系数决定
        d2 = d1.groupby('Bucket', as_index = True)
        r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)    #　？　？　？    # 以斯皮尔曼系数作为分箱终止条件
        n = n - 1
    d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
    d3['min']=d2.min().X    #  min 就是分箱的节点
    d3['max'] = d2.max().X
    d3['sum'] = d2.sum().Y
    d3['total'] = d2.count().Y
    d3['rate'] = d2.mean().Y
    d3['woe']=np.log((d3['rate']/(1-d3['rate']))/(good/bad))
    d3['goodattribute']=d3['sum']/good
    d3['badattribute']=(d3['total']-d3['sum'])/bad
    iv=((d3['goodattribute']-d3['badattribute'])*d3['woe']).sum()   #返回 iv
    d4 = (d3.sort_index(by = 'min')).reset_index(drop=True)    # 返回 d  
    print("=" * 60)
    print(d4)
    woe=list(d4['woe'].round(3))             #返回 woe
    cut=[]    #  cut 存放箱段节点
    cut.append(float('-inf'))  # 在 列表前加 -inf 
    for i in range(1,n+1):            # n 是前面的 分箱的 分割数  ，所以 分成n+1份
         qua=X.quantile(i/(n+1))     #quantile 分为数  得到分箱的节点
         cut.append(round(qua,4))   # 保留4位小数       #返回cut
    cut.append(float('inf')) # 在列表后加  inf
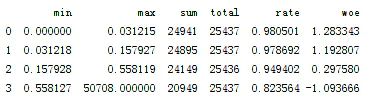
    return d4,iv,cut,woe

针对我们将使用最优分段对于数据集中的RevolvingUtilizationOfUnsecuredLines、age、DebtRatio和MonthlyIncome进行分类。

图5-1 RevolvingUtilizationOfUnsecuredLines分箱情况.png

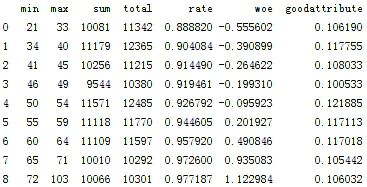
图5-2 age分箱情况.png

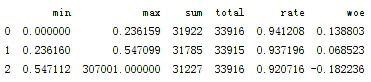
图5-3 DebtRatio分箱情况.png

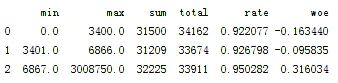
图5-4 MonthlyIncome分箱情况.png

针对不能最优分箱的变量，分箱如下：

对于上述分箱方法不能合理拆分的特征，采用无监督分箱--手动分箱：

    # 连续变量离散化
pinf = float('inf')#正无穷大
ninf = float('-inf')#负无穷大
cutx3 = [ninf, 0, 1, 3, 5, pinf]
cutx6 = [ninf, 1, 2, 3, 5, 7, 9, pinf]   #加了 7，9  
cutx7 = [ninf, 0, 1, 3, 5, pinf]
cutx8 = [ninf, 0,1,2, 3, pinf]
cutx9 = [ninf, 0, 1, 3, pinf]
cutx10 = [ninf, 0, 1, 2, 3, 5, pinf]

def self_bin(Y,X,cat):#自定义人工分箱函数
    good=Y.sum()   #好用户数量
    bad=Y.count()-good   # 坏用户数量
    d1=pd.DataFrame({'X':X,'Y':Y,'Bucket':pd.cut(X,cat)}) #建立个数据框 X-- 各个特征变量 ， Y--用户好坏标签 ， Bucket--各个分箱
    d2=d1.groupby('Bucket', as_index = True)     #  按分箱分组聚合 ，并且社会为 Index
    d3 = pd.DataFrame(d2.X.min(), columns=['min'])  #  添加 min 列 ,不用管里面的 d2.X.min()
    d3['min'] = d2.min().X    #求每个箱段内 X 比如 家庭人数的最小值
    d3['max'] = d2.max().X    #求每个箱段内 X 比如 家庭人数的最大值
    d3['sum'] = d2.sum().Y    #求每个箱段内 Y 好客户的个数
    d3['total'] = d2.count().Y  #求每个箱段内  总共客户数
    d3['rate'] = d2.mean().Y    # 好客户率
    #WOE的全称是“Weight of Evidence”，即证据权重。WOE是对原始自变量的一种编码形式。是为了 计算 iv 准备的
    #要对一个变量进行WOE编码，需要首先把这个变量进行分组处理（也叫离散化、分箱等等，说的都是一个意思）
    d3['woe'] = np.log((d3['rate'] / (1 - d3['rate'])) / (good / bad))   
    d3['goodattribute'] = d3['sum'] / good     # 每个箱段内 好用户 占 总好用户数  的 比率
    d3['badattribute'] = (d3['total'] - d3['sum']) / bad  # 每个箱段内 坏用户 占 总坏用户数 的 比率
    #IV的全称是Information Value，中文意思是信息价值，或者信息量。  通俗的说 就是 变量的预测能力
    iv = ((d3['goodattribute'] - d3['badattribute']) * d3['woe']).sum()
    d4 = (d3.sort_index(by='min'))   #数据框 的 按 min 升序排列
    woe = list(d4['woe'].round(3))
    return d4, iv,woe
#对他们就行分箱处理：

dfx3,ivx3,woex3 = self_bin(trainDf.SeriousDlqin2yrs,trainDf['NumberOfTime30-59DaysPastDueNotWorse'], cutx3)
dfx6,ivx6 ,woex6= self_bin(trainDf.SeriousDlqin2yrs, trainDf['NumberOfOpenCreditLinesAndLoans'], cutx6)
dfx7,ivx7,woex7 = self_bin(trainDf.SeriousDlqin2yrs, trainDf['NumberOfTimes90DaysLate'], cutx7)
dfx8, ivx8,woex8 = self_bin(trainDf.SeriousDlqin2yrs, trainDf['NumberRealEstateLoansOrLines'], cutx8)
dfx9, ivx9,woex9 = self_bin(trainDf.SeriousDlqin2yrs, trainDf['NumberOfTime60-89DaysPastDueNotWorse'], cutx9)
dfx10,ivx10,woex10 = self_bin(trainDf.SeriousDlqin2yrs, trainDf['NumberOfDependents'], cutx10)

5.2 WOE

WoE分析， 是对指标分箱、计算各个档位的WoE值并观察WoE值随指标变化的趋势。其中WoE的数学定义是:
woe=ln(goodattribute/badattribute)
在进行分析时，我们需要对各指标从小到大排列，并计算出相应分档的WoE值。其中正向指标越大，WoE值越小；反向指标越大，WoE值越大。正向指标的WoE值负斜率越大，反响指标的正斜率越大，则说明指标区分能力好。WoE值趋近于直线，则意味指标判断能力较弱。若正向指标和WoE正相关趋势、反向指标同WoE出现负相关趋势，则说明此指标不符合经济意义，则应当予以去除。
woe函数实现在上一节的mono_bin()函数里面已经包含，这里不再重复。

5.3 相关性分析和IV筛选

接下来，我们会用经过清洗后的数据看一下变量间的相关性。注意，这里的相关性分析只是初步的检查，进一步检查模型的VI（证据权重）作为变量筛选的依据。
相关性图我们通过Python里面的seaborn包，调用heatmap()绘图函数进行绘制，实现代码如下：

 

    corr = data.corr()#计算各变量的相关性系数
    xticks = ['x0','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']#x轴标签
    yticks = list(corr.index)#y轴标签
    fig = plt.figure()
    ax1 = fig.add_subplot(1, 1, 1)
    sns.heatmap(corr, annot=True, cmap='rainbow', ax=ax1, annot_kws={'size': 9, 'weight': 'bold', 'color': 'blue'})#绘制相关性系数热力图
    ax1.set_xticklabels(xticks, rotation=0, fontsize=10)
    ax1.set_yticklabels(yticks, rotation=0, fontsize=10)
    plt.show()

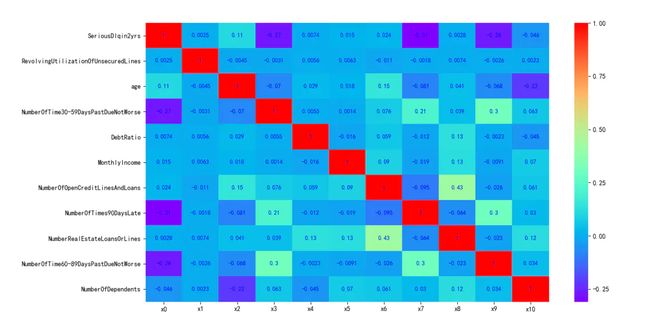
生成的图形如图5-5所示：

 

图5-5 数据集各变量的相关性

由上图可以看出，各变量之间的相关性是非常小的。NumberOfOpenCreditLinesAndLoans和NumberRealEstateLoansOrLines的相关性系数为0.43。
接下来，我进一步计算每个变量的Infomation Value（IV）。IV指标是一般用来确定自变量的预测能力。 其公式为：
IV=sum((goodattribute-badattribute)*ln(goodattribute/badattribute))
通过IV值判断变量预测能力的标准是：
< 0.02: unpredictive
0.02 to 0.1: weak
0.1 to 0.3: medium
0.3 to 0.5: strong
> 0.5: suspicious
IV的实现放在mono_bin()函数里面，

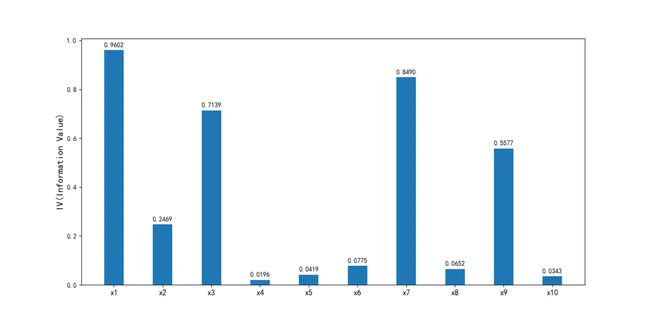
生成的IV图代码：

    ivlist=[ivx1,ivx2,ivx3,ivx4,ivx5,ivx6,ivx7,ivx8,ivx9,ivx10]#各变量IV
    index=['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']#x轴的标签
    fig1 = plt.figure(1)
    ax1 = fig1.add_subplot(1, 1, 1)
    x = np.arange(len(index))+1
    ax1.bar(x, ivlist, width=0.4)#生成柱状图
    ax1.set_xticks(x)
    ax1.set_xticklabels(index, rotation=0, fontsize=12)
    ax1.set_ylabel('IV(Information Value)', fontsize=14)
    #在柱状图上添加数字标签
    for a, b in zip(x, ivlist):
        plt.text(a, b + 0.01, '%.4f' % b, ha='center', va='bottom', fontsize=10)
    plt.show()

输出图像：

 

图5-6 输出的各变量IV图

可以看出，DebtRatio、MonthlyIncome、NumberOfOpenCreditLinesAndLoans、NumberRealEstateLoansOrLines和NumberOfDependents变量的IV值明显较低，所以予以删除。

小结

本文主要介绍了信用评分模型开发过程中的数据预处理、探索性分析和变量选择。数据预处理主要针对缺失值用随机森林法和直接剔除法进行处理，对于异常值主要根据实际情况和箱形图的数据分布，对异常值进行剔除；探索性分析主要对各变量的分布情况进行初始的探究；变量选择主要考虑了变量的分箱方法，根据分箱结果计算WOE值，然后检查变量之间的相关性，根据各变量的IV值来选择对数据处理有好效果的变量。
接下来会介绍信用评分模型的模型开发、模型评估和信用评分等。

 

上一篇文章基于Python的信用评分卡模型分析（一）已经介绍了信用评分卡模型的数据预处理、探索性数据分析、变量分箱和变量选择等。接下来我们将继续讨论信用评分卡的模型实现和分析，信用评分的方法和自动评分系统。

六、模型分析

证据权重（Weight of Evidence,WOE）转换可以将Logistic回归模型转变为标准评分卡格式。引入WOE转换的目的并不是为了提高模型质量，只是一些变量不应该被纳入模型，这或者是因为它们不能增加模型值，或者是因为与其模型相关系数有关的误差较大，其实建立标准信用评分卡也可以不采用WOE转换。这种情况下，Logistic回归模型需要处理更大数量的自变量。尽管这样会增加建模程序的复杂性，但最终得到的评分卡都是一样的。
在建立模型之前，我们需要将筛选后的变量转换为WoE值，便于信用评分。

6.1 WOE转换

我们已经能获取了每个变量的分箱数据和woe数据，只需要根据各变量数据进行替换，实现代码如下：

#替换成woe函数
def replace_woe(series,cut,woe):
    list=[]
    i=0
    while i=0:
            if value>=cut[j]:
                j=-1
            else:
                j -=1
                m -= 1
        list.append(woe[m])
        i += 1
    return list

我们将每个变量都进行替换,并将其保存到WoeData.csv文件中：

    # 替换成woe
    data['RevolvingUtilizationOfUnsecuredLines'] = Series(replace_woe(data['RevolvingUtilizationOfUnsecuredLines'], cutx1, woex1))
    data['age'] = Series(replace_woe(data['age'], cutx2, woex2))
    data['NumberOfTime30-59DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, woex3))
    data['DebtRatio'] = Series(replace_woe(data['DebtRatio'], cutx4, woex4))
    data['MonthlyIncome'] = Series(replace_woe(data['MonthlyIncome'], cutx5, woex5))
    data['NumberOfOpenCreditLinesAndLoans'] = Series(replace_woe(data['NumberOfOpenCreditLinesAndLoans'], cutx6, woex6))
    data['NumberOfTimes90DaysLate'] = Series(replace_woe(data['NumberOfTimes90DaysLate'], cutx7, woex7))
    data['NumberRealEstateLoansOrLines'] = Series(replace_woe(data['NumberRealEstateLoansOrLines'], cutx8, woex8))
    data['NumberOfTime60-89DaysPastDueNotWorse'] = Series(replace_woe(data['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, woex9))
    data['NumberOfDependents'] = Series(replace_woe(data['NumberOfDependents'], cutx10, woex10))
    data.to_csv('WoeData.csv', index=False)

6.2 Logisic模型建立

我们直接调用statsmodels包来实现逻辑回归：

    导入数据
    data = pd.read_csv('WoeData.csv')
    #应变量
    Y=data['SeriousDlqin2yrs']
    #自变量，剔除对因变量影响不明显的变量
    X=data.drop(['SeriousDlqin2yrs','DebtRatio','MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines','NumberOfDependents'],axis=1)
    X1=sm.add_constant(X)
    logit=sm.Logit(Y,X1)
    result=logit.fit()
    print(result.summary())

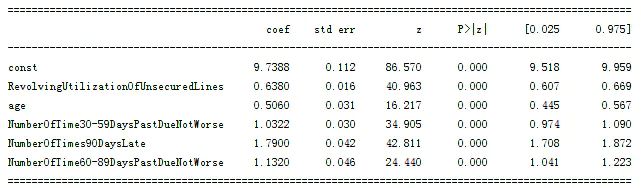
输出结果：

 

图6-1 逻辑回归模型结果.png

通过图6-1可知，逻辑回归各变量都已通过显著性检验，满足要求。

6.3 模型检验

到这里，我们的建模部分基本结束了。我们需要验证一下模型的预测能力如何。我们使用在建模开始阶段预留的test数据进行检验。通过ROC曲线和AUC来评估模型的拟合能力。
在Python中，可以利用sklearn.metrics，它能方便比较两个分类器，自动计算ROC和AUC。
实现代码：

    #应变量
    Y_test = test['SeriousDlqin2yrs']
    #自变量，剔除对因变量影响不明显的变量，与模型变量对应
    X_test = test.drop(['SeriousDlqin2yrs', 'DebtRatio', 'MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines', 'NumberOfDependents'], axis=1)
    X3 = sm.add_constant(X_test)
    resu = result.predict(X3)#进行预测
    fpr, tpr, threshold = roc_curve(Y_test, resu)
    rocauc = auc(fpr, tpr)#计算AUC
    plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % rocauc)#生成ROC曲线
    plt.legend(loc='lower right')
    plt.plot([0, 1], [0, 1], 'r--')
    plt.xlim([0, 1])
    plt.ylim([0, 1])
    plt.ylabel('真正率')
    plt.xlabel('假正率')
    plt.show()

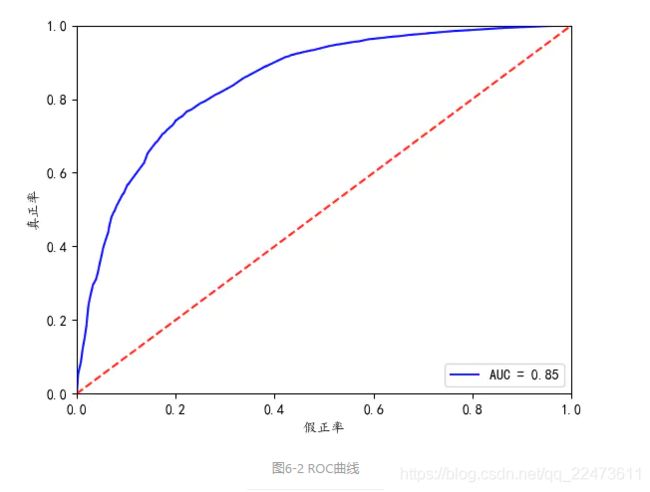
输出结果：

 

从上图可知，AUC值为0.85，说明该模型的预测效果还是不错的，正确率较高。

七、信用评分

我们已经基本完成了建模相关的工作，并用ROC曲线验证了模型的预测能力。接下来的步骤，就是将Logistic模型转换为标准评分卡的形式。

7.1 评分标准

 

 

依据以上论文资料得到：
a=log（p_good/P_bad）
Score = offset + factor * log(odds)
在建立标准评分卡之前，我们需要选取几个评分卡参数：基础分值、 PDO（比率翻倍的分值）和好坏比。 这里， 我们取600分为基础分值，PDO为20 （每高20分好坏比翻一倍），好坏比取20。

    # 计算分数
    # coe为逻辑回归模型的系数
    coe = [9.738849, 0.638002, 0.505995, 1.032246, 1.790041, 1.131956]
    # 我们取600分为基础分值，PDO为20（每高20分好坏比翻一倍），好坏比取20。
    p = 20 / math.log(2)  # p= 28.85390081777927
    q = 600 - 20 * math.log(20) / math.log(2)  #513.5614381022527
    baseScore = round(q + p * coe[0], 0)  #795.0
 

个人总评分=基础分+各部分得分

7.2 部分评分

下面计算各变量部分的分数。各部分得分函数：

 

#计算分数函数
def get_score(coe,woe,factor):
    scores=[]
    for w in woe:
        score=round(coe*w*factor,0)
        scores.append(score)
    return scores

计算各变量得分情况：

    # 各项部分分数
    x1 = get_score(coe[1], woex1, p)
    x2 = get_score(coe[2], woex2, p)
    x3 = get_score(coe[3], woex3, p)
    x7 = get_score(coe[4], woex7, p)
    x9 = get_score(coe[5], woex9, p)

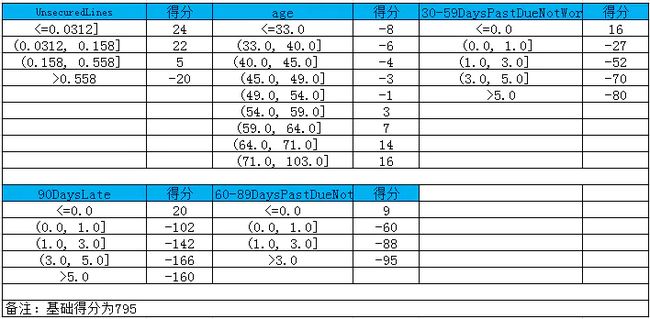
我们可以得到各部分的评分卡如图7-1所示：

图7-1 各变量的评分标准

八、自动评分系统

根据变量来计算分数，实现如下：

#根据变量计算分数
def compute_score(series,cut,score):
    list = []
    i = 0
    while i < len(series):
        value = series[i]
        j = len(cut) - 2
        m = len(cut) - 2
        while j >= 0:
            if value >= cut[j]:
                j = -1
            else:
                j -= 1
                m -= 1
        list.append(score[m])
        i += 1
    return list

我们来计算test里面的分数：

    test1 = pd.read_csv('TestData.csv')
    test1['BaseScore']=Series(np.zeros(len(test1)))+baseScore
    test1['x1'] = Series(compute_score(test1['RevolvingUtilizationOfUnsecuredLines'], cutx1, x1))
    test1['x2'] = Series(compute_score(test1['age'], cutx2, x2))
    test1['x3'] = Series(compute_score(test1['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, x3))
    test1['x7'] = Series(compute_score(test1['NumberOfTimes90DaysLate'], cutx7, x7))
    test1['x9'] = Series(compute_score(test1['NumberOfTime60-89DaysPastDueNotWorse'], cutx9, x9))
    test1['Score'] = test1['x1'] + test1['x2'] + test1['x3'] + test1['x7'] +test1['x9']  + baseScore
    test1.to_csv('ScoreData.csv', index=False)

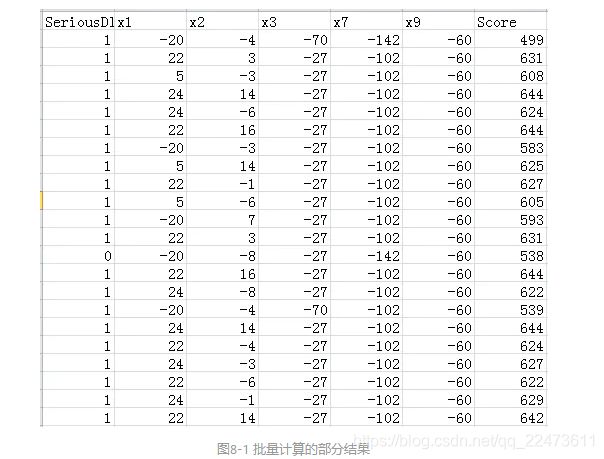
批量计算的部分分结果：

九、总结以及展望

本文通过对kaggle上的Give Me Some Credit数据的挖掘分析，结合信用评分卡的建立原理，从数据的预处理、变量选择、建模分析到创建信用评分，创建了一个简单的信用评分系统。
基于AI 的机器学习评分卡系统可通过把旧数据（某个时间点后，例如2年）剔除掉后再进行自动建模、模型评估、并不断优化特征变量，使得系统更加强大。

 

 

 

 

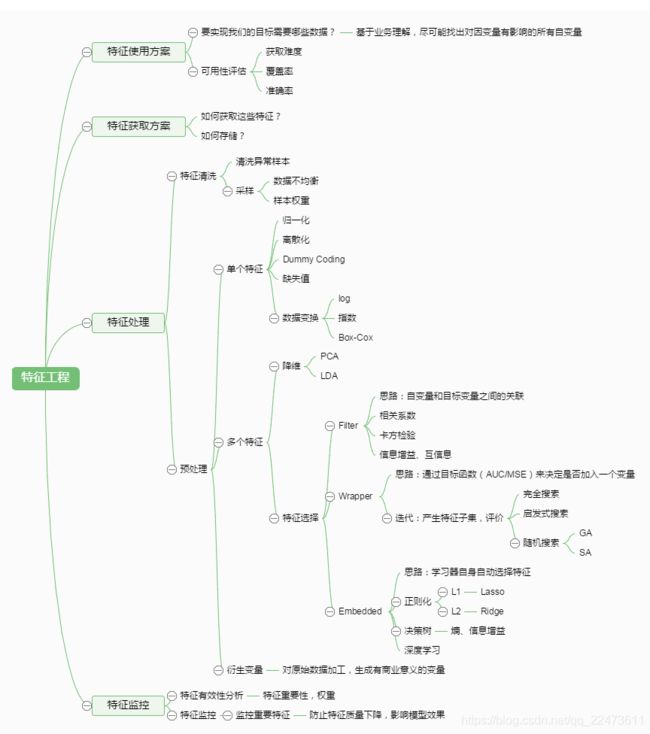
构建信用风险类型的特征

在我们运用模型之前，我们首先要进行特征工程，其本质是一项工程活动，目的是最大限度地从原始数据中提取特征以供算法和模型使用。特征处理是特征工程的核心部分，sklearn提供了较为完整的特征处理方法，包括数据预处理，特征选择，降维等。

https://www.cnblogs.com/jasonfreak/p/5448385.html

 

 

评分卡模型开发-基于逻辑回归的标准评分卡实现

https://www.csdn.net/gather_2c/Mtjakg3sNjQ5LWJsb2cO0O0O.html

由逻辑回归的基本原理，我们将客户违约的概率表示为p，则正常的概率为1-p。因此，可以得到：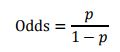

此时，客户违约的概率p可表示为：

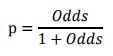
评分卡设定的分值刻度可以通过将分值表示为比率对数的线性表达式来定义，即可表示为下式：

其中，A和B是常数。式中的负号可以使得违约概率越低，得分越高。通常情况下，这是分值的理想变动方向，即高分值代表低风险，低分值代表高风险。
逻辑回归模型计算比率如下所示：

其中，用建模参数拟合模型可以得到模型参数β0，β1，…，βn。
式中的常数A、B的值可以通过将两个已知或假设的分值带入计算得到。通常情况下，需要设定两个假设：
（1）给某个特定的比率设定特定的预期分值；
（2）确定比率翻番的分数（PDO）
根据以上的分析，我们首先假设比率为x的特定点的分值为P。则比率为2x的点的分值应该为P+PDO。代入式中，可以得到如下两个等式：

假设 设定评分卡刻度使得比率为{1:20}（违约正常比）时的分值为50分，PDO为10分，代入式中求得：B=14.43，A=6.78
则分值的计算公式可表示为：

评分卡刻度参数A和B确定以后，就可以计算比率和违约概率，以及对应的分值了。通常将常数A称为补偿，常数B称为刻度。
则评分卡的分值可表达为：

式中：变量x1…xn是出现在最终模型中的自变量，即为入模指标。由于此时所有变量都用WOE转换进行了转换，可以将这些自变量中的每一个都写(βiωij)δij的形式：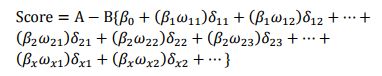

式中ωij 为第i行第j个变量的WOE，为已知变量；βi为逻辑回归方程中的系数，为已知变量；δij为二元变量，表示变量i是否取第j个值。上式可重新表示为：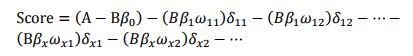

此式即为最终评分卡公式。如果x1…xn变量取不同行并计算其WOE值，式中表示的标准评分卡格式，如表3.20所示：
表3.20表明，变量x1有k1行，变量x2有k2行，以此类推；基础分值等于(A−Bβ0)；由于分值分配公式中的负号，模型参数β0，β1，…，βn也应该是负值；变量xi的第j行的分值取决于以下三个数值：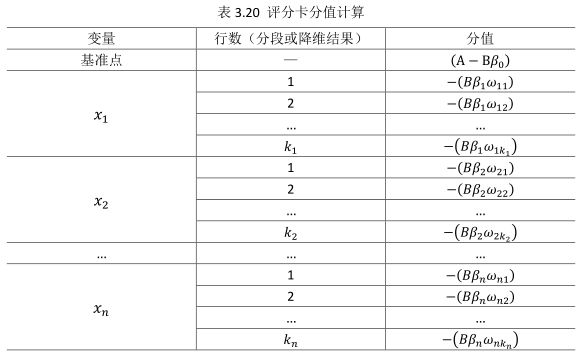

（1）刻度因子B；
（2）逻辑回归方程的参数βi；
（3）该行的WOE值，ωij
综上，我们详细讲述了模型开发及生成标准评分卡各步骤的处理结果，自动生成标准评分卡的R完整代码：

library(klaR)
library(InformationValue)
data(GermanCredit)
train_kfold<-sample(nrow(GermanCredit),800,replace = F)
train_kfolddata<-GermanCredit[train_kfold,]   #提取样本数据集
test_kfolddata<-GermanCredit[-train_kfold,]   #提取测试数据集
credit_risk<-ifelse(train_kfolddata[,"credit_risk"]=="good",0,1)
#将违约样本用“1”表示，正常样本用“0”表示。
tmp<-train_kfolddata[,-21]
data<-cbind(tmp,credit_risk)
quant_vars<-c("duration","amount","installment_rate","present_residence","age",
              "number_credits","people_liable","credit_risk")
             #获取定量指标
quant_GermanCredit<-data[,quant_vars]  #提取定量指标

#逐步回归法，获取自变量中对违约状态影响最显著的指标
base.mod<-lm(credit_risk~1,data = quant_GermanCredit)
#获取线性回归模型的截距
all.mod<-lm(credit_risk~.,data = quant_GermanCredit)
#获取完整的线性回归模型
stepMod<-step(base.mod,scope = list(lower=base.mod,upper=all.mod),
              direction = "both",trace = 0,steps = 1000)
#采用双向逐步回归法，筛选变量
shortlistedVars<-names(unlist(stepMod[[1]]))
#获取逐步回归得到的变量列表
shortlistedVars<-shortlistedVars[!shortlistedVars %in%"(Intercept)"]
#删除逐步回归的截距
print(shortlistedVars)
#输出逐步回归后得到的变量
quant_model_vars<-c("duration","amount","installment_rate","age")
#完成定量入模指标
#提取数据集中全部的定性指标
factor_vars<-c("status","credit_history","purpose","savings","employment_duration",
               "personal_status_sex","other_debtors","property",
               "other_installment_plans","housing","job","telephone","foreign_worker")
               #获取所有名义变量
all_iv<-data.frame(VARS=factor_vars,IV=numeric(length(factor_vars)),
                   STRENGTH=character(length(factor_vars)),stringsAsFactors = F)
                  #初始化待输出的数据框
for(factor_var in factor_vars)
{
  all_iv[all_iv$VARS==factor_var,"IV"]<-InformationValue::IV(X=
  data[,factor_var],Y=data$credit_risk)  
  #计算每个指标的IV值
  all_iv[all_iv$VARS==factor_var,"STRENGTH"]<-attr(InformationValue::IV(X=
  data[,factor_var],Y=data$credit_risk),"howgood")  
  #提取每个IV指标的描述
}
all_iv<-all_iv[order(-all_iv$IV),]    #排序IV
qual_model_vars<-subset(all_iv,STRENGTH=="Highly Predictive")[1:5,]
qual_model_vars<-c("status","credit_history","savings","purpose","property")

#连续变量分段和离散变量降维
#1.变量duration
library(smbinning)
result<-smbinning(df=data,y="credit_risk",x="duration",p=0.05)
result$ivtable

duration_Cutpoint<-c()
duration_WoE<-c()
duration<-data[,"duration"]
for(i in 1:length(duration))
{
  if(duration[i]<=8)
  {
    duration_Cutpoint[i]<-"<= 8"
    duration_WoE[i]<--1.5670
  }
  if(duration[i]<=33&duration[i]>8)
  {
    duration_Cutpoint[i]<-"<= 33"
    duration_WoE[i]<--0.0924
  }
  if(duration[i]> 33)
  {
    duration_Cutpoint[i]<-"> 33"
    duration_WoE[i]<-0.7863
  }
}
#2.变量amount
result<-smbinning(df=data,y="credit_risk",x="amount",p=0.05)
result$ivtable
amount_Cutpoint<-c()
amount_WoE<-c()
amount<-data[,"amount"]
for(i in 1:length(amount))
{
  if(amount[i]<= 3913)
  {
    amount_Cutpoint[i]<-"<= 3913"
    amount_WoE[i]<--0.2536
  }
  if(amount[i]<= 9283&amount[i]> 3913)
  {
    amount_Cutpoint[i]<-"<= 9283"
    amount_WoE[i]<-0.4477
  }
  if(amount[i]> 9283)
  {
    amount_Cutpoint[i]<-"> 9283"
    amount_WoE[i]<-1.3109
  }
}
#3.变量age
result<-smbinning(df=data,y="credit_risk",x="age",p=0.05)
result$ivtable
age_Cutpoint<-c()
age_WoE<-c()
age<-data[,"age"]
for(i in 1:length(age))
{
  if(age[i]<= 34)
  {
    age_Cutpoint[i]<-"<= 34"
    age_WoE[i]<-0.2279
  }
  if(age[i] > 34)
  {
    age_Cutpoint[i]<-" > 34"
    age_WoE[i]<--0.3059
  }
}
#4.变量installment_rate等距分段
install_data<-data[,c("installment_rate","credit_risk")]
tb1<-table(install_data)
total<-list()
for(i in 1:nrow(tb1))
{
  total[i]<-sum(tb1[i,])
}
t.tb1<-cbind(tb1,total)
goodrate<-as.numeric(t.tb1[,"0"])/as.numeric(t.tb1[,"total"])
badrate<-as.numeric(t.tb1[,"1"])/as.numeric(t.tb1[,"total"])
gb.tbl<-cbind(t.tb1,goodrate,badrate)
Odds<-goodrate/badrate
LnOdds<-log(Odds)
tt.tb1<-cbind(gb.tbl,Odds,LnOdds)
WoE<-log((as.numeric(tt.tb1[,"0"])/700)/(as.numeric(tt.tb1[,"1"])/300))
all.tb1<-cbind(tt.tb1,WoE)
all.tb1
installment_rate_Cutpoint<-c()
installment_rate_WoE<-c()
installment_rate<-data[,"installment_rate"]
for(i in 1:length(installment_rate))
{
  if(installment_rate[i]==1)
  {
    installment_rate_Cutpoint[i]<-"=1"
    installment_rate_WoE[i]<-0.06252036
  }
  if(installment_rate[i]==2)
  {
    installment_rate_Cutpoint[i]<-"=2"
    installment_rate_WoE[i]<-0.1459539
  }
  if(installment_rate[i]==3)
  {
    installment_rate_Cutpoint[i]<-"=3"
    installment_rate_WoE[i]<--0.03937517
  }
  if(installment_rate[i]==4)
  {
    installment_rate_Cutpoint[i]<-"=4"
    installment_rate_WoE[i]<--0.1657562
  }
}
#定性指标的降维和WoE
discrete_data<-data[,c("status","credit_history","savings","purpose",
                       "property","credit_risk")]
summary(discrete_data)
#对purpose指标进行降维
x<-discrete_data[,c("purpose","credit_risk")]
d<-as.matrix(x)
for(i in 1:nrow(d))
{
  #合并car(new)、car(used)
  if(as.character(d[i,"purpose"])=="car (new)")  
  {
    d[i,"purpose"]<-as.character("car(new/used)")
  }
  if(as.character(d[i,"purpose"])=="car (used)")
  {
    d[i,"purpose"]<-as.character("car(new/used)")
  }
  #合并radio/television、furniture/equipment
  if(as.character(d[i,"purpose"])=="radio/television") 
  {
    d[i,"purpose"]<-as.character("radio/television/furniture/equipment")
  }
  if(as.character(d[i,"purpose"])=="furniture/equipment")
  {
    d[i,"purpose"]<-as.character("radio/television/furniture/equipment")
  }
  #合并others、repairs、business
  if(as.character(d[i,"purpose"])=="others")
  {
    d[i,"purpose"]<-as.character("others/repairs/business")
  }
  if(as.character(d[i,"purpose"])=="repairs")
  {
    d[i,"purpose"]<-as.character("others/repairs/business")
  }
  if(as.character(d[i,"purpose"])=="business")
  {
    d[i,"purpose"]<-as.character("others/repairs/business")
  }
  #合并retraining、education
  if(as.character(d[i,"purpose"])=="retraining")
  {
    d[i,"purpose"]<-as.character("retraining/education")
  }
  if(as.character(d[i,"purpose"])=="education")
  {
    d[i,"purpose"]<-as.character("retraining/education")
  }
}

new_data<-cbind(discrete_data[,c(-4,-6)],d)
#替换原数据集中的“purpose”指标的值
woemodel<-woe(credit_risk~.,data = new_data,zeroadj=0.5,applyontrain=TRUE)
woemodel$woe
#1.status
status<-as.matrix(new_data[,"status"])
colnames(status)<-"status"
status_WoE<-c()
for(i in 1:length(status))
{
  if(status[i]=="... < 100 DM")
  {
    status_WoE[i]<--0.8671300
  }
  if(status[i]=="0 <= ... < 200 DM")
  {
    status_WoE[i]<--0.4240681
  }
  if(status[i]=="... >= 200 DM / salary for at least 1 year")
  {
    status_WoE[i]<-0.4129033
  }
  if(status[i]=="no checking account")
  {
    status_WoE[i]<-1.2237524
  }
}
#2.credit_history
credit_history<-as.matrix(new_data[,"credit_history"])
colnames(credit_history)<-"credit_history"
credit_history_WoE<-c()
for(i in 1:length(credit_history))
{
  if(credit_history[i]=="no credits taken/all credits paid back duly")
  {
    credit_history_WoE[i]<--1.53771824
  }
  if(credit_history[i]=="all credits at this bank paid back duly")
  {
    credit_history_WoE[i]<--1.00079000
  }
  if(credit_history[i]=="existing credits paid back duly till now")
  {
    credit_history_WoE[i]<--0.09646414
  }
  if(credit_history[i]=="delay in paying off in the past")
  {
    credit_history_WoE[i]<--0.01996074
  }
  if(credit_history[i]=="critical account/other credits existing")
  {
    credit_history_WoE[i]<-0.77276102
  }
}
#3.savings
savings<-as.matrix(new_data[,"savings"])
colnames(savings)<-"savings"
savings_WoE<-c()
for(i in 1:length(savings))
{
  if(savings[i]=="... < 100 DM")
  {
    savings_WoE[i]<--0.3051490
  }
  if(savings[i]=="100 <= ... < 500 DM")
  {
    savings_WoE[i]<--0.2267733
  }
  if(savings[i]=="500 <= ... < 1000 DM")
  {
    savings_WoE[i]<-0.8340112
  }
  if(savings[i]=="... >= 1000 DM")
  {
    savings_WoE[i]<-1.1739617
  }
  if(savings[i]=="unknown/no savings account")
  {
    savings_WoE[i]<-0.7938144
  }
}
#4.property
property<-as.matrix(new_data[,"property"])
colnames(property)<-"property"
property_WoE<-c()
for(i in 1:length(property))
{
  if(property[i]=="real estate")
  {
    property_WoE[i]<-0.49346566
  }
  if(property[i]=="building society savings agreement/life insurance")
  {
    property_WoE[i]<--0.16507975
  }
  if(property[i]=="car or other")
  {
    property_WoE[i]<-0.08054425
  }
  if(property[i]=="unknown/no property")
  {
    property_WoE[i]<--0.65586969
  }
}
#5.purpose
purpose<-as.matrix(new_data[,"purpose"])
colnames(purpose)<-"purpose"
purpose_WoE<-c()
for(i in 1:length(purpose))
{
  if(purpose[i]=="car(new/used)")
  {
    purpose_WoE[i]<--0.11260594
  }
  if(purpose[i]=="domestic appliances")
  {
    purpose_WoE[i]<-0.53602528
  }
  if(purpose[i]=="others/repairs/business")
  {
    purpose_WoE[i]<--0.09146793
  }
  if(purpose[i]=="radio/television/furniture/equipment")
  {
    purpose_WoE[i]<--0.23035114
  }
  if(purpose[i]=="retraining/education")
  {
    purpose_WoE[i]<--0.43547619
  }
}
#入模定量和定性指标
model_data<-cbind(data[,quant_model_vars],data[,qual_model_vars])
#入模定量和定性指标的WOE
credit_risk<-as.matrix(data[,"credit_risk"])
colnames(credit_risk)<-"credit_risk"
model_data_WOE<-as.data.frame(cbind(duration_WoE,amount_WoE,age_WoE,
                installment_rate_WoE,status_WoE,credit_history_WoE,
                savings_WoE,property_WoE,purpose_WoE,credit_risk))
#入模定量和定性指标“分段”
model_data_Cutpoint<-cbind(duration_Cutpoint,amount_Cutpoint,age_Cutpoint,
                     installment_rate_Cutpoint,status,credit_history,
                     savings,property,purpose)
#逻辑回归
m<-glm(credit_risk~.,data=model_data_WOE,family = binomial())
alpha_beta<-function(basepoints,baseodds,pdo)
{
  beta<-pdo/log(2)
  alpha<-basepoints+beta*log(baseodds)
  return(list(alpha=alpha,beta=beta))
}
coefficients<-m$coefficients
#通过指定特定比率（1/20）的特定分值（50）和比率翻番的分数（10），来计算评分卡的系数alpha和beta
x<-alpha_beta(50,0.05,10)
#计算基础分值
basepoint<-round(x$alpha-x$beta*coefficients[1])
#1.duration_score
duration_score<-round(as.matrix(-(model_data_WOE[,"duration_WoE"]*
                                    coefficients["duration_WoE"]*x$beta)))
colnames(duration_score)<-"duration_score"
#2.amount_score
amount_score<-round(as.matrix(-(model_data_WOE[,"amount_WoE"]*
                                  coefficients["amount_WoE"]*x$beta)))
colnames(amount_score)<-"amount_score"
#3.age_score
age_score<-round(as.matrix(-(model_data_WOE[,"age_WoE"]*
                                  coefficients["age_WoE"]*x$beta)))
colnames(age_score)<-"age_score"
#4.installment_rate_score
installment_rate_score<-round(as.matrix(-(model_data_WOE[,"installment_rate_WoE"]*
                                  coefficients["installment_rate_WoE"]*x$beta)))
colnames(installment_rate_score)<-"installment_rate_score"
#5.status_score
status_score<-round(as.matrix(-(model_data_WOE[,"status_WoE"]*
                               coefficients["status_WoE"]*x$beta)))
colnames(status_score)<-"status_score"
#6.credit_history_score
credit_history_score<-round(as.matrix(-(model_data_WOE[,"credit_history_WoE"]*
                                  coefficients["credit_history_WoE"]*x$beta)))
colnames(credit_history_score)<-"credit_history_score"
#7.savings_score
savings_score<-round(as.matrix(-(model_data_WOE[,"savings_WoE"]*
                                          coefficients["savings_WoE"]*x$beta)))
colnames(savings_score)<-"savings_score"
#8.property_score
property_score<-round(as.matrix(-(model_data_WOE[,"property_WoE"]*
                                   coefficients["property_WoE"]*x$beta)))
colnames(property_score)<-"property_score"
#9.purpose_score
purpose_score<-round(as.matrix(-(model_data_WOE[,"purpose_WoE"]*
                                    coefficients["purpose_WoE"]*x$beta)))
colnames(purpose_score)<-"purpose_score"
#输出最终的CSV格式的打分卡
#1.基础分值
r1<-c("","basepoint",20)
m1<-matrix(r1,nrow = 1)
colnames(m1)<-c("Basepoint","Basepoint","Score")
#2.duration的分值
duration_scoreCard<-cbind(as.matrix(c("Duration","",""),ncol=1),
                    unique(cbind(duration_Cutpoint,duration_score)))
#View(duration_scoreCard)
#3.amount的分值
amount_scoreCard<-cbind(as.matrix(c("Amount","",""),ncol=1),
                          unique(cbind(amount_Cutpoint,amount_score)))
#View(amount_scoreCard)
#4.age的分值
age_scoreCard<-cbind(as.matrix(c("Age",""),ncol=1),
                        unique(cbind(age_Cutpoint,age_score)))
#View(age_scoreCard)
#5.installment_rate的分值
installment_rate_scoreCard<-cbind(as.matrix(c("Installment_rate","","",""),ncol=1),
                     unique(cbind(installment_rate_Cutpoint,installment_rate_score)))
#View(installment_rate_scoreCard)
#6.status的分值
status_scoreCard<-cbind(as.matrix(c("Status","","",""),ncol=1),
                                  unique(cbind(status,status_score)))
#View(status_scoreCard)
#7.credit_history的分值
credit_history_scoreCard<-cbind(as.matrix(c("Credit_history","","","",""),ncol=1),
                        unique(cbind(credit_history,credit_history_score)))
#View(credit_history_scoreCard)
#8.savings的分值
savings_scoreCard<-cbind(as.matrix(c("Savings","","","",""),ncol=1),
                                unique(cbind(savings,savings_score)))
#View(savings_scoreCard)
#9.property的分值
property_scoreCard<-cbind(as.matrix(c("Property","","",""),ncol=1),
                         unique(cbind(property,property_score)))
#View(property_scoreCard)
#10.purpose的分值
purpose_scoreCard<-cbind(as.matrix(c("Purpose","","","",""),ncol=1),
                          unique(cbind(purpose,purpose_score)))
#View(purpose_scoreCard)
scoreCard_CSV<-rbind(m1,duration_scoreCard,amount_scoreCard,age_scoreCard,
                     installment_rate_scoreCard,status_scoreCard,credit_history_scoreCard,
                     savings_scoreCard,property_scoreCard,purpose_scoreCard)
#将标准评分卡输出到项目文件中，且命名为ScoreCard.CSV，调整格式即可得到标准评分卡
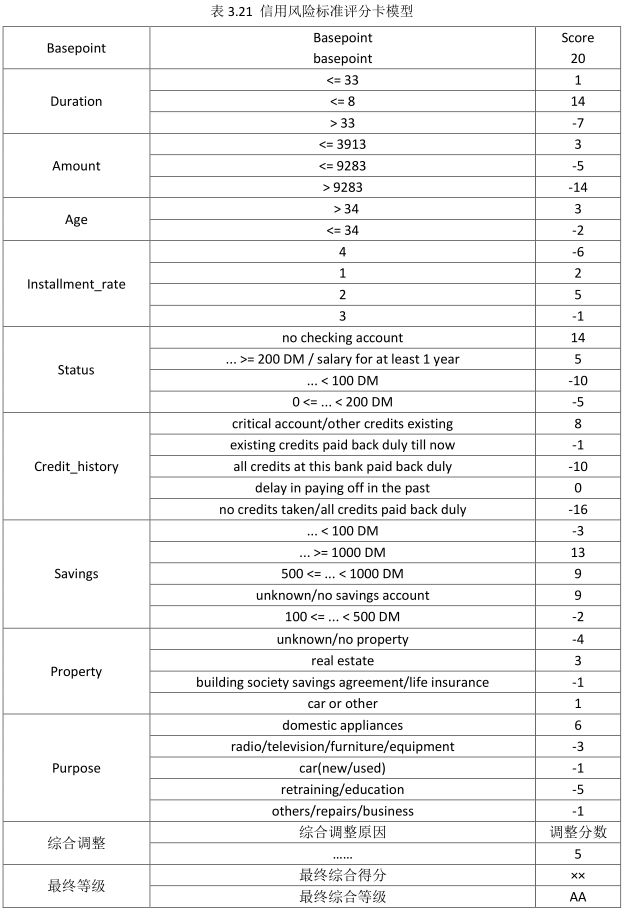
write.csv(scoreCard_CSV,"C:/Users/ZL/Desktop/creditcard_model/ScoreCard.CSV")

需要特别说明的是，上述开发的信用风险评级模型只包含定量和定性两部分，在实际的使用中还要充分考虑到信用风险的特定，增加综合调整部分，以应对可能对客户信用影响较大的突发事件，如客户被刑事起诉、遭遇重大疾病等。完整的信用风险标准评分卡模型，如表3.21所示：

使用小样本开发信用风险评级模型时，通常采用交叉验证（如五折交叉验证）的方法以提高模型的稳定性。由于上述代码采用的是随机抽样，每次抽取样本总体的80%作为样本集，来进行模型开发，剩余样本总体的20%用作模型测试。模型开发过程中，只需要运行上述代码4次，并对得到的标准评分卡、模型中每项的分值取平均值，即可得到最终的标准评分卡模型。