神经网络技巧篇之寻找最优超参数
在神经网络中,除了权重和偏置等参数外,超参数也是一个很常见且重要的参数,这里的超参数是指,比如各层的神经元数量、batch大小、参数更新时的学习率或权值衰减等,如果这些超参数没有设置一个合适的值,模型的性能就会很差。
那如何设置好这个超参数呢?一般都是不断地试错,在这个过程中尽可能高效的找到这个参数。需要注意的是,在评估这个超参数性能的时候,不能使用测试数据来评估,因为使用测试数据就会使得这个超参数对测试数据过拟合,那可能就会导致泛化能力低,这个时候我们一般采取专用的确认数据,一般称为验证数据(validation data),最后才使用测试数据来确认泛化能力。
验证数据,我们可以使用np.random.shuffle来随机选取打乱的数据作为验证数据,下面的方法使用了permutation,也是打乱顺序,区别在于permutation不会更改原来的数组,是拷贝了一份再进行洗牌的,而shuffle会修改原来的值,需看情况来使用。
def shuffle_dataset(x,t):
'''
打乱数据集的训练数据和测试数据
permutation不会修改原数组,shuffle将会修改x,t
'''
p=np.random.permutation(x.shape[0])
x=x[p]
t=t[p]
return x,t超参数是在设定一个大致的范围里面进行随机采样,然后用这个值去评估识别的精度。重复操作,我们观察识别精度的结果,逐步确定超参数的合适范围。超参数的随机采样代码:
weight_decay=10**np.random.uniform(-8, -4)#权值衰减的范围在10的-8次方到-4次方之间
lr=10**np.random.uniform(-6, -2)#学习率的范围在10的-6次方到-2次方之间下面还是基于MNIST数据集来观察验证数据和训练数据的识别精度的比较
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.trainer import Trainer
def shuffle_dataset(x,t):
'''
打乱数据集的训练数据和测试数据
permutation不会修改原数组,shuffle将会修改x,t
'''
p=np.random.permutation(x.shape[0])
x=x[p]
t=t[p]
return x,t
(x_train,t_train),(x_test,t_test)=load_mnist(normalize=True)
x_train=x_train[:500]#(500,784)
t_train=t_train[:500]
#验证数据(示例为选取训练数据中20%的数据)
validation_rate=0.2
validation_num=int(x_train.shape[0]*validation_rate)
x_train,t_train=shuffle_dataset(x_train,t_train)
x_val=x_train[:validation_num]#(100, 784)
t_val=t_train[:validation_num]#(100,)
x_train=x_train[validation_num:]#(400, 784)
t_train=t_train[validation_num:]#(400,)
#print(x_val.shape,t_val.shape,x_train.shape,t_train.shape)
def _train(weight_decay,lr,epochs=50):
network=MultiLayerNet(inputSize=784,hiddenSizeList=[100,100,100,100,100,100],outputSize=10,weight_decay_lambda=weight_decay)
trainer=Trainer(network,x_train,t_train,x_val,t_val,epochs=epochs,mini_batch_size=100,optimizer='SGD',optimizer_param={'lr':lr},verbose=False)
trainer.train()
return trainer.test_acc_list,trainer.train_acc_list
#超参数的随机搜索
results_val={}
results_train={}
for _ in range(50):
#选定在这个范围里面搜索
weight_decay=10**np.random.uniform(-8,-4)
lr=10**np.random.uniform(-6,-2)
val_acc_list,train_acc_list=_train(weight_decay,lr)
print('验证精度:'+str(val_acc_list[-1])+' | 学习率:'+str(lr)+',权值衰减:'+str(weight_decay))
key='lr:'+str(lr)+',w_decay:'+str(weight_decay)
results_val[key]=val_acc_list#学习率和权值组合成key
results_train[key]=train_acc_list
#画图
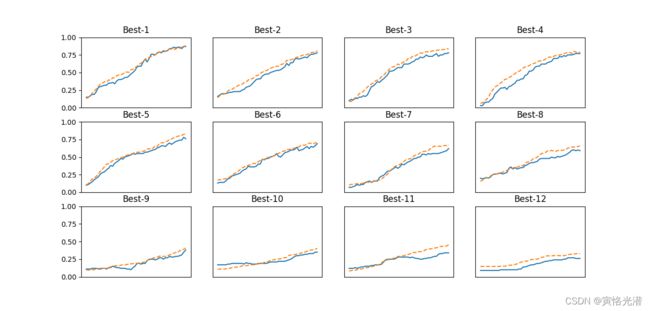
print('----最优超参数降序排列的结果---')
i=0
for key,val_acc_list in sorted(results_val.items(),key=lambda x:x[1][-1],reverse=True):
print('最优验证精度:'+str(val_acc_list[-1])+' | '+key)
plt.subplot(3,4,i+1)
plt.title('Best-'+str(i+1))
plt.ylim(0.0,1.0)
if i%4:plt.yticks([])
plt.xticks([])
x=np.arange(len(val_acc_list))
plt.plot(x,val_acc_list)
plt.plot(x,results_train[key],'--')
i+=1
if i>=12:
break
plt.show()
从打印的数据可以看出,学习率在0.001~0.01以及权值衰减系数在10的-8次方~10的-6次方之间,学习进行的顺利,同样的重复这个操作,我们就可以逐步减小这个寻找范围,直到找到非常合适的超参数。
由此可见,参数的重要性不言而喻,对寻找最优参数的方法感兴趣的伙伴们可以参阅:
神经网络技巧篇之寻找最优参数的方法![]() https://blog.csdn.net/weixin_41896770/article/details/121375510神经网络技巧篇之寻找最优参数的方法【续】
https://blog.csdn.net/weixin_41896770/article/details/121375510神经网络技巧篇之寻找最优参数的方法【续】![]() https://blog.csdn.net/weixin_41896770/article/details/121419590
https://blog.csdn.net/weixin_41896770/article/details/121419590