利用ARIMA模型对房价进行预测
所有代码与解析
ARIMA模型我理解也不是太好,建议大家学习的话去B站搜一下ARIMA找个视频看就可以了,我这个代码在jupyter是跑通的,如果有问题可以按照方格放入jupyter跑
#!/usr/bin/env python
# coding: utf-8
# In[2]:
get_ipython().run_line_magic('load_ext', 'autoreload')
get_ipython().run_line_magic('autoreload', '2')
get_ipython().run_line_magic('matplotlib', 'inline')
get_ipython().run_line_magic('config', "InlineBackend.figure_format = 'retina'")
import sys
import os
import numpy as np
import pandas as pd
import datetime
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.tsa.api as smt
from scipy.interpolate import lagrange
from statsmodels.tsa.stattools import adfuller #ADF检验
from statsmodels.stats.diagnostic import acorr_ljungbox #白噪声检验
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf #画图定阶
from statsmodels.tsa.arima_model import ARIMA #模型
from statsmodels.tsa.arima_model import ARMA #模型
from statsmodels.stats.stattools import durbin_watson #DW检验
from statsmodels.graphics.api import qqplot #qq图
from sklearn.model_selection import train_test_split #划分数据集
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
# In[3]:
data = pd.read_excel(r'F:\I_love_learning\junior\数据挖掘与数据仓库\课程设计\dataroom2.xlsx')
#data
# In[4]:
#X_train , X_test , y_train,y_test = train_test_split(data_day.index,data_day['单价'],test_size=0.25,random_state=0)
# In[5]:
#data_train = pd.DataFrame(y_train)
#data_test = pd.DataFrame(y_test)
#data_train
# In[6]:
data_ana = data[['单价','挂牌时间']].groupby(by = '挂牌时间').mean()
data_ana.sort_index(inplace = True)
#data_ana = data_ana[data_ana.index >datetime.datetime(2019,12,1)]
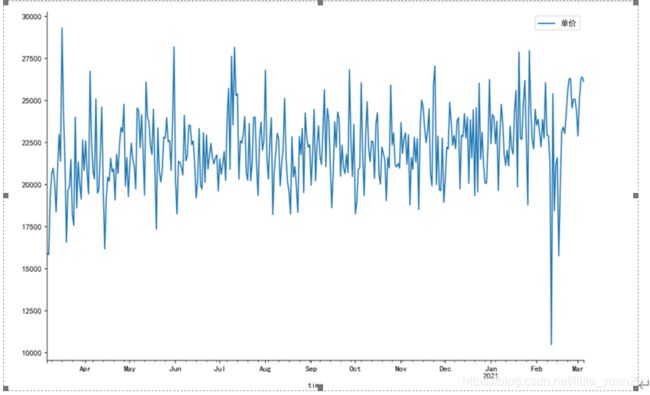
data_ana.plot()
plt.show()
# In[7]:
data_per = data_ana[data_ana.index >= datetime.datetime(2020,1,1)]
data_per.reset_index(inplace = True)
#data_per
# In[8]:
#选取一月到三月的值
date_se = pd.DataFrame({'time':pd.date_range('2020/3/6','2021/3/7')})
#date_se
# In[9]:
#外连接之后拉格朗日填补缺失值
data_day = pd.merge(date_se,data_per,left_on ='time',right_on = '挂牌时间',how = 'outer')
del data_day['挂牌时间']
def na_c(s,n,k=5):
y = s.reindex(list(range(n-k, n)) + list(range(n+1, n+1+k))) #取数不报错代码段
y = y[y.notnull()] # 剔除空值
return(lagrange(y.index,list(y))(n))
# 创建函数,做插值,由于数据量原因,以空值前后5个数据(共10个数据)为例做插值
na_re = []
for i in range(len(data_day['单价'])):
if data_day['单价'].isnull()[i]:
data_day['单价'][i] = na_c(data_day['单价'],i)
print(na_c(data_day['单价'],i))
na_re.append(data_day['单价'][i])
data_day = data_day.dropna()
#data_day
# In[10]:
data_day.set_index('time',inplace = True)
#data_day
# In[60]:
data_train = data_day['2020/3/6':'2021/3/5']
data_test = data_day['2021/3/6':'2021/3/7']
#data_test
# In[61]:
data_train.head()
# In[62]:
data_train.plot(figsize = (12,8))
sns.despine()
# In[63]:
def stationarity(timeseries): #平稳性处理:差分法
#差分法(不平稳处理),保存成新的列,1阶差分,dropna() 删除缺失值
diff1 = timeseries.diff(1).dropna()
diff2 = diff1.diff(1) #在一阶查分基础上做二阶查分
diff1.plot(color = 'red',title='diff 1',figsize=(10,4))
diff2.plot(color = 'black',title='diff 2',figsize=(10,4))
#滚动平均(平滑法不平稳处理)
rolmean = timeseries.rolling(window=4,center = False).mean()
#滚动标准差
rolstd = timeseries.rolling(window=4,center = False).std()
rolmean.plot(color = 'yellow',title='Rolling Mean',figsize=(10,4))
rolstd.plot(color = 'blue',title='Rolling Std',figsize=(10,4))
#ADF检验
x = np.array(diff1['单价'])
adftest = adfuller(x, autolag='AIC')
print (adftest)
#白噪声检验
p_value = acorr_ljungbox(timeseries, lags=1)
print (p_value)
# In[64]:
stationarity(data_train)
'''
ADT检验
(1) 1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较,ADF Test result同时小于1%、5%、10%即说明非常好地拒绝该假设,本数据中,adf结果为-6.9, 小于三个level的统计值。
(2)P-value是否非常接近0.本数据中,P-value 为 6.21e-23,接近0。
ADT检验结果说明数据平稳
非白噪声检验
统计量的P值约为0.0085,小于显著性水平0.05,则可以以95%的置信水平拒绝原假设,认为序列为非白噪声序列(否则,接受原假设,认为序列为纯随机序列。)
'''
# In[ ]:
# In[ ]:
# In[65]:
def tsplot(y, lags = None, title = '', figsize = (14,8)):
fig = plt.figure(figsize = figsize)
layout = (2,2)
ts_ax = plt.subplot2grid(layout , (0,0))
hist_ax = plt.subplot2grid(layout , (0,1))
acf_ax = plt.subplot2grid(layout , (1,0))
pacf_ax = plt.subplot2grid(layout , (1,1))
y.plot(ax=ts_ax)
ts_ax.set_title(title)
y.plot(ax = hist_ax, kind = 'hist', bins = 25)
hist_ax.set_title('Histogram')
smt.graphics.plot_acf(y, lags = lags, ax = acf_ax)
smt.graphics.plot_pacf(y, lags=lags, ax=pacf_ax)
[ax.set_xlim(0) for ax in [acf_ax, pacf_ax]]
sns.despine()
fig.tight_layout()
return ts_ax, acf_ax, pacf_ax
# In[ ]:
# In[66]:
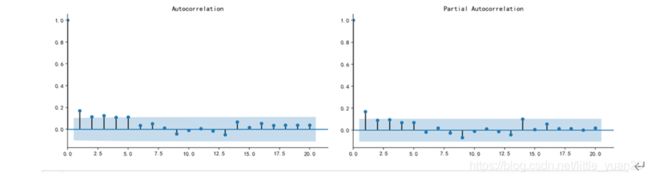
tsplot(data_train, title = 'data', lags = 20)
# In[67]:
arima200 = sm.tsa.SARIMAX(data_train, order = (2,0,0))
model_results = arima200.fit()
# In[68]:
import itertools
p_min = 0
d_min = 1
q_min = 0
p_max = 6
d_max = 1
q_max = 3
# Initialize a DataFrame to store the results
results_bic = pd.DataFrame(
index=['AR{}'.format(i) for i in range(p_min, p_max + 1)],
columns=['MA{}'.format(i) for i in range(q_min, q_max + 1)])
for p, d, q in itertools.product(
range(p_min, p_max + 1), range(d_min, d_max + 1),
range(q_min, q_max + 1)):
if p == 0 and d == 0 and q == 0:
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = np.nan
continue
try:
model = sm.tsa.SARIMAX(
data_train,
order=(p, d, q),
#enforce_stationarity=False,
#enforce_invertibility=False,
)
results = model.fit()
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = results.bic
except:
continue
results_bic = results_bic[results_bic.columns].astype(float)
# In[69]:
#模型选择bic:贝叶斯信息准则:选择最小的值
fig, ax = plt.subplots(figsize=(10, 8))
ax = sns.heatmap(results_bic,
mask=results_bic.isnull(),
ax=ax,
annot=True,
fmt='.2f',
);
ax.set_title('BIC');
# In[70]:
data_diff = data_train.diff()
data_diff = data_diff.dropna()
# In[71]:
train_results = sm.tsa.arma_order_select_ic(
data_diff, ic=['aic', 'bic'], trend='nc', max_ar=6, max_ma=3)
print('AIC', train_results.aic_min_order)
print('BIC', train_results.bic_min_order)
# In[72]:
model = ARIMA(data_train, order = (0,1,1))
# In[73]:
result = model.fit()
print(result.summary())
# In[74]:
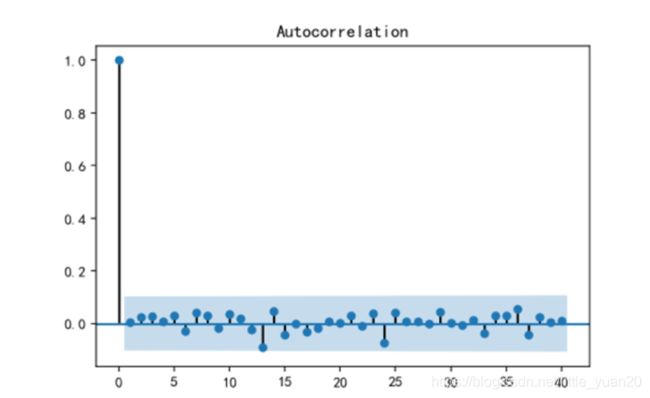
#模型自回归残差检验
model = sm.tsa.ARIMA(data_train, order=(0, 1, 1))
results = model.fit()
resid = results.resid #赋值
fig = plt.figure(figsize=(12,8))
fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40)
plt.show()
# In[75]:
#pred = result.predict('20210305','20210309',dynamic = True)
pred = result.predict('20210101','20210307',dynamic = True,typ = 'levels')
#pred
# In[76]:
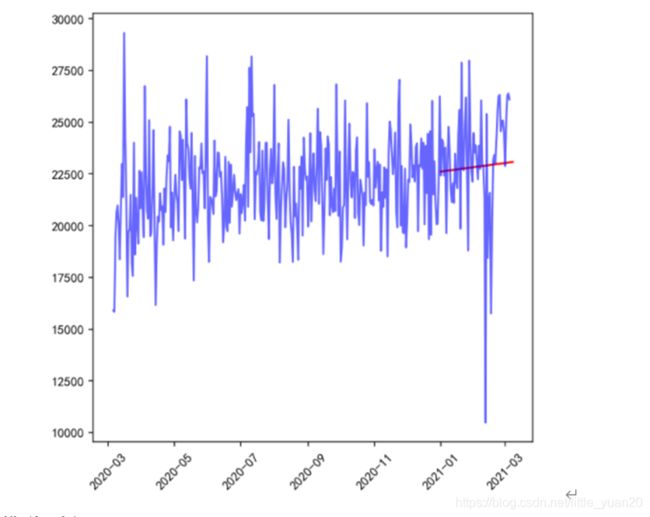
plt.figure(figsize=(6, 6))
plt.xticks(rotation=45)
plt.plot(pred,color = 'red')
plt.plot(data_train, color = 'blue',alpha = 0.6)
# In[77]:
model_results.plot_diagnostics(figsize = (16,12))
# In[78]:
#data_test
# In[81]:
data_train.tail(20)
# In[79]:
pred.tail(3)
一、 数据获取
通过request+BeautifulSoup对天津每个区的房屋价格数据进行爬取,并与小区数据进行合并得到经纬度
二、 数据预处理
三、 分析模型(ARIMA)
得出差分法平稳性操作较好,一阶差分和二阶差分差距不大
2) 探索平滑法进行数据平稳性操作
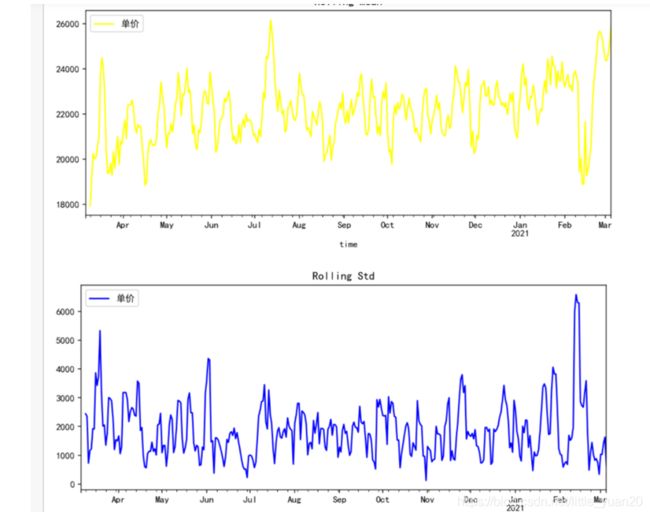
1%、%5、%10不同程度拒绝原假设的统计值和ADF Test result的比较,ADF Test result同时小于1%、5%、10%即说明非常好地拒绝该假设,本数据中,adf结果为-8.32, 小于三个level的统计值。
P-value是否非常接近0.本数据中,P-value 为 3e-13,接近0
可以得出结论,一阶差分后的数据是平稳的
4) 白噪声检验

统计量的P值约为0.001,小于显著性水平0.05,则可以以95%的置信水平拒绝原假设,认为序列为非白噪声序列(否则,接受原假设,认为序列为纯随机序列。)
模型分析:
QQ图呈一条直线, 通过qq图可以看出,残差基本满足了正态分布。