MATLAB:ode45
ode45
ode45实际上是数值分析中数值求解微分方程组的一种方法,4阶五级Runge-Kutta算法。
调用方法
[t,x]=ode45(Fun,tspan,x0,options,pars)
其实这种方程的每一个状态变量都是t的函数,我们可以从现代控制理论的状态空间来想。因此返回[ t,x ],其中t是一个列向量,x是n×n的矩阵,它的每一列就是其中一个状态变量随t的变化值。
t返回列向量的时间点X返回对应T的求解列向量
之后定义.m函数亦或是匿名函数f = @ ( t , x )来描述微分方程组的右边部分,并且是列向量。(注意匿名函数一定是先t后x并且一定有t占位)
EG1:
%三维点或线图 - MATLAB plot3 - MathWorks 中国
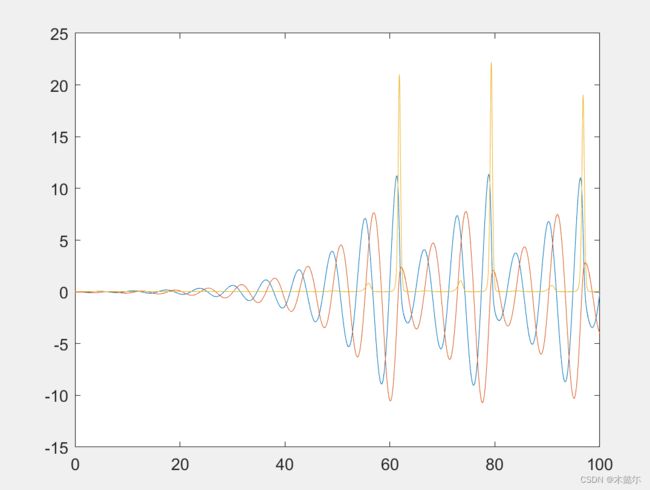
f = @(t,x)[-x(2)-x(3);x(1)+0.2*x(2);0.2+(x(1)-5.7)*x(3)];
[t,y] = ode45(f,[0,100],[0;0;0]);
plot(t,y);
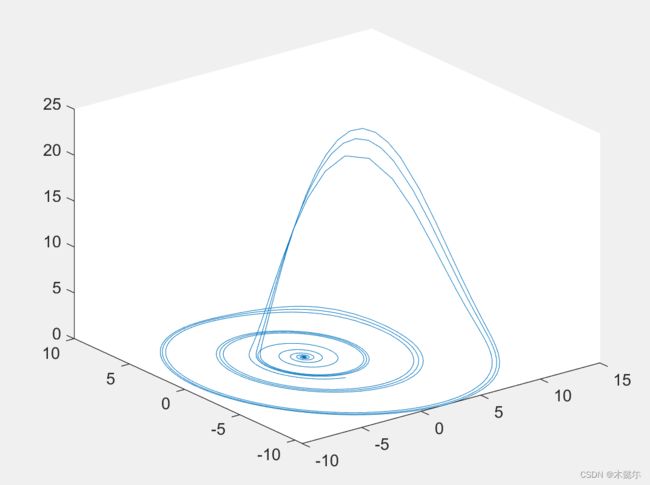
figure;
plot3(y(:,1),y(:,2),y(:,3))
f = @(t,x)[-x(2)-x(3);x(1)+0.2*x(2);0.2+(x(1)-5.7)*x(3)];
[t,y] = ode45(f,[0,100],[0;0;0]);
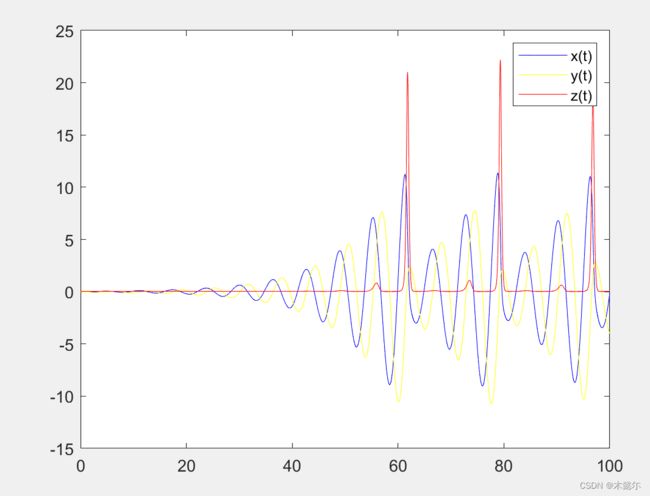
plot(t,y(:,1),"b")
hold on
plot(t,y(:,2),"y")
plot(t,y(:,3),"r")
legend("x(t)","y(t)","z(t)");
figure;
plot3(y(:,1),y(:,2),y(:,3))%第一列,第二列,第三列分别为x,y,z的数据做成三维图
求解非刚性微分方程 - 中阶方法 - MATLAB ode45 - MathWorks 中国