隐马尔可夫模型与序列标注详解

目录

第4章 隐马尔可夫模型与序列标注

4.1 序列标注问题

4.2 隐马尔可夫模型

4.3 隐马尔可夫模型的样本生成

4.4 隐马尔可夫模型的训练

4.5 隐马尔可夫模型的预测

4.6 隐马尔可夫模型应用于中文分词

4.7 性能评测

4.8 总结

第4章 隐马尔可夫模型与序列标注

比如这句话：

头上戴着束发嵌宝紫金冠，齐眉勒着二龙抢珠金抹额

加粗词语是现代入相对陌生的两个“新词”，但我们依然认识它们。当读者读到“戴着”时，心里就已经开始期待一个描述帽饰的名词了。另外，既然存在“披肩”这样的构词法，那么“抹额”的含义也就不难猜测了。人类不需要死记硬背整部词典，而拥有动态组词的能力，生搬硬套现代汉语词典的话，反而查不到这两个饰品词汇。 这说明词语级别的模型天然缺乏OOV召回能力，我们需要更细颗粒度的模型。比词语更细的颗粒就是字符，如果字符级模型能够掌握汉字组词的规律，那么它就能够由字构词、动态地识别新词汇，而不局限于词典了。 具体说来，只要将每个汉字组词时所处的位置(首尾等)作为标签，则中文分词就转化为给定汉字序列找出标签序列的问题。一般而言，由字构词是序列标注模型的一种应用。 在所有“序列标注”模型中，隐马尔可夫模型是最基础的一种。 本章先介绍序列标注问题的定义及应用，然后讲述并实现隐马尔可夫模型，最终将其应用到中文分词上去。

序列标注指的是给定一个序列x=x1x2…xn，找出序列中每个元素对应标签y=y1y2…yn的问题。其中y所有可能的取值集合称为标注集（tagset）。比如，输入一个自然数序列，输出它们的奇偶性，按顺序排列成另一个序列。此时标注集为｛奇，偶｝，标注过程如图4-1所示。图4-1序列标注的最简示例

数字奇偶性的判断只取决于当前元素，这是最简单的情况。然而，大多数情况下，需要考虑前后元素以及之前的标签才能决定当前标签。比如扑克牌游戏“小猫钓鱼”中，双方轮流出牌，第一次出现相同牌时出牌人收走相同两张牌之间的所有牌。如果将出牌顺序记录为序列x，出牌后是否应当收牌作为标签序列y，那么游戏就转化为序列标注问题了，如图4-2所示。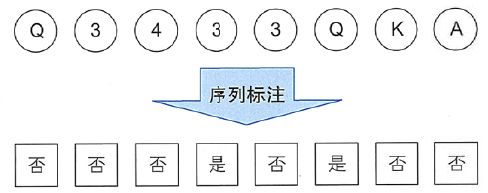图4-2小猫钓鱼转化为序列标注问题

注意这三次出3时是否收牌的标签都不一样，因为根据游戏规则，只有第二次出3时桌上才有相同牌，而第三次出3时前两次的已经被收走了，所以第三次不会触发收牌。 求解序列标注问题的模型一般称为序列标注器（tagger），通常由模型从一个标注数据集{X,Y}={(xi,yi)},i=1,…,K中学习相关知识后再进行预测。在NLP问题中，x通常是字符或词语，而y则是待预测的组词角色或词性等标签。无论是第3章介绍的中文分词、第7章中的词性标注还是第8章中的命名实体识别，都可以转化为序列标注问题。

4.1.1 序列标注与中文分词

考虑一个字符序列（字符串）x，想象切词器真的是在拿刀切割字符串。那么每个字符xi，在分词时无非充当如下两种角色：要么在i之后切开，要么跳过不切。如此，中文分词转化为标注集为{切，过}的序列标注问题，如图4-3所示。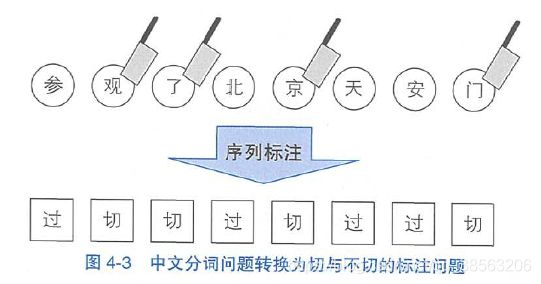图4-3中文分词问题转换为切与不切的标注问题

只要标注器正确标注每个字符切与不切，分词器就能够按照指示切割出正确结果。可以将标注序列看作中文分词的中间结果，往后则是纯粹的字符串分割逻辑。 分词标注集并非只有一种。为了捕捉汉字分别作为词语首尾（Begin、End）、词中（Middle）以及单字成词（Single）时不同的成词概率，人们提出了{B，M，E，S}这种最流行的标注集，如图4-4所示。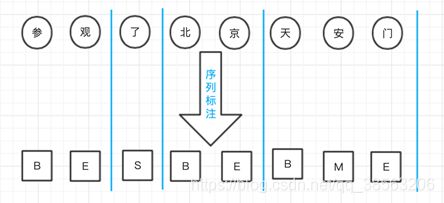图4-4中文分词序列标注的BMES标注集

标注后，分词器将最近两个BE标签对应区间内的所有字符合并为一个词语，S标签对应字符作为单字词语，按顺序输出即完成分词过程。

4.1.2 序列标注与词性标注

词性标注任务是一个天然的序列标注问题：x是单词序列，y是相应的词性序列。需要综合考虑前后的单词与词性才能决定当前单词的词性。如图4-5所示。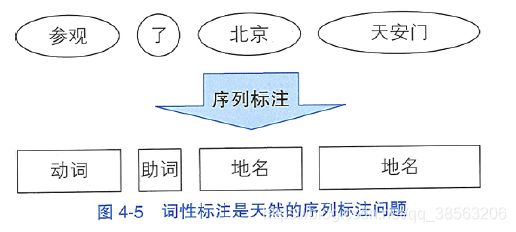图4-5词性标注是天然的序列标注问题

词性标注集同样不是唯一的，人们根据需要制定了不同的标注集。其中最著名的当数863标注集和北大标注集，前者词性数量要少一些，颗粒度要大一些。本书将在第7章中详细介绍这些标注集和相应语料库。 词性标注与“小猫钓鱼”类似，需要综合考虑前后的单词与词性才能决定当前单词的词性。比如副词容易接续动词，“的”字之后容易出现名词。这里的“容易”其实意味着较大的概率，需要使用概率模型去模拟。

4.1.3 序列标注与命名实体识别

所谓命名实体，指的是现实存在的实体，比如人名、地名和机构名。命名实体是OOV的主要组成部分，往往也是句子中最令人关注的成分。命名实体的数量是无穷的，因为世界上每种事物都需要一个名字代表自身。比如每颗星星、每种蛋白质都有自己的名称，宇宙中的星星和蛋白质显然不可数。 简短的人名和地名可以通过中文分词切分，然后通过词性标注来确定所属类别。但地名和机构名常常由多个单词组成（称为复合词），较难识别。由于复合词的丰度较小，导致分词器和词性标注器很难一步到位地将其识别出来，这时常常在分词和词性标注的中间结果之上进行召回。 考虑到字符级别中文分词和词语级别命名实体识别有着类似的特点，都是组合短单位形成长单位的问题。所以命名实体识别可以复用BMES标注集，并沿用中文分词的逻辑，只不过标注的对象由字符变为单词而已。唯一不同的是，命名实体识别还需要确定实体所属的类别。这个额外的要求依然是个标注问题，可以通过将命名实体类别附着到BMES标签来达到目的。比如，构成地名的单词标注为“B/M/E/S-地名”，以此类推。对于那些不构成命名实体的单词，则统-标注为O ( Outside), 即复合词之外。一个典型样本如图4-6所示。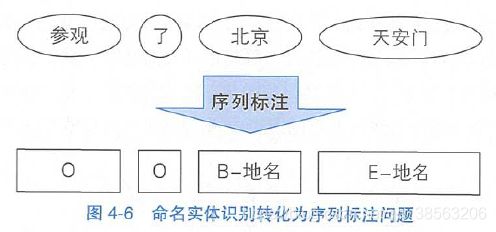图4-6命名实体识别转化为序列标注问题 图4-6后续过程中，命名实体识别模块根据标注结果，将“北京”和“天安门”作为首尾组合成词，并且标注为地名。 总之，序列标注问题是NLP中最常见的问题之一。许多应用任务都可以变换思路，转化为序列标注来解决。所以一个准确的序列标注模型非常重要，直接关系到NLP系统的准确率。机器学习领域为NLP提供了许多标注模型，本着循序渐进的原则，本章介绍其中最基础的一个隐马尔可夫模型。

4.2 隐马尔可夫模型

隐马尔可夫模型( Hidden Markov Model, HMM)是描述两个时序序列联合分布 p(x,y) 的概率模型: x 序列外界可见(外界指的是观测者)，称为观测序列(obsevation sequence); y 序列外界不可见，称为状态序列(state sequence)。比如观测 x 为单词，状态 y 为词性，我们需要根据单词序列去猜测它们的词性。隐马尔可夫模型之所以称为“隐”，是因为从外界来看，状态序列(例如词性)隐藏不可见，是待求的因变量。从这个角度来讲，人们也称状态为隐状态(hidden state),而称观测为显状态( visible state)。隐马尔可夫模型之所以称为“马尔可夫模型”，”是因为它满足马尔可夫假设。 接下来我们先复习一下马尔可夫假设，然后再过渡到隐马尔可夫模型的详细介绍。

4.2.1 从马尔可夫假设到隐马尔可夫模型

在第3章语言模型中，我们曾讲过马尔可夫假设：每个事件的发生概率只取决于前一个事件。将满足该假设的连续多个事件串联在一起，就构成了马尔可夫链。在NLP的语境下，可以将事件具象为单词，于是马尔可夫模型就具象为二元语法模型。 马尔可夫假设：每个事件的发生概率只取决于前一个事件。 马尔可夫链：将满足马尔可夫假设的连续多个事件串联起来，就构成了马尔可夫链。

如果把事件具象为单词，那么马尔可夫模型就具象为二元语法模型。

在此基础之上，隐马尔可夫模型理解起来就并不复杂了：

隐马尔可夫模型：它的马尔可夫假设作用于状态序列，

假设 ① 当前状态 Yt 仅仅依赖于前一个状态 Yt-1， 连续多个状态构成隐马尔可夫链 y。有了隐马尔可夫链，如何与观测序列 x 建立联系呢？

隐马尔可夫模型做了第二个假设: ② 任意时刻的观测 x 只依赖于该时刻的状态 Yt，与其他时刻的状态或观测独立无关。如果用箭头表示事件的依赖关系(箭头终点是结果，依赖于起点的因缘)，则隐马尔可夫模型可以表示为下图所示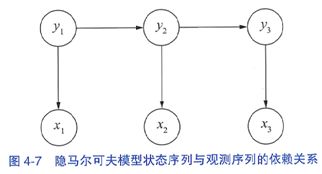

这张图也许有一丝违和感，按通常理解，应当是x决定y，而不是反过来。这是由于在联合概率分布p(x,y)中，两个随机变量并没有固定的先后与因果关系，即p(x,y)=p(y,x)。从贝叶斯定理的角度来讲，联合分布完全可以做两种等价变换： p(x,y）=p(x)p(y|x)=p(y)p(x|y) 隐马尔可夫模型只不过在假设②中釆用了后一种变换而已，即假定先有状态，后有观测，取决于两个序列的可见与否。这种因果关系在现实生活中也能找到例子，比如写文章可以想象为先在脑海中构思好一个满足语法的词性序列，然后再将每个词性填充为具体的词语。 状态与观测之间的依赖关系确定之后，隐马尔可夫模型利用三个要素来模拟时序序列的发生过程----即初始状态概率向量、状态转移概率矩阵和发射概率矩阵，在接下来的三个小节中分别介绍。

4.2.2 初始状态概率向量

系统启动时进入的第一状态y1称为初始状态，假设y有N种可能的取值，即y∈{s1,…,sn}，那么y1就是一个独立的离散型随机变量，由p(y1|π)描述。其中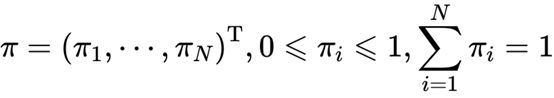是概率分布的参数向量，称为初始状态概率向量。让我们把它添加到示意图上，如图虚线所示。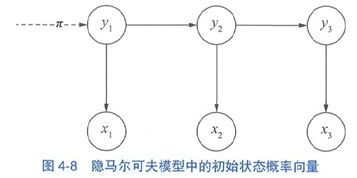给定π，初始状态y1的取值分布就确定了。比如中文分词问题采用{B,M,E,S}标注集时，y1所有可能的取值及对应概率如下： P(y1=B)=0.7 P(y1=M)=0 P(y1=E)=0 P(y1=s)=0.3

那么此时隐马尔可夫模型的初始状态概率向量为π= [0.7,0,0,0.3]。注意标签M和E的概率为0，因为句子第一个字符不可能成为单词的中部或尾部。另外，p(y1=B)>p(y1=S)，也说明句子第一个词是单字的可能性要小一些。

4.2.3 状态转移矩阵

Yt 如何转移到 Yt+1 呢？根据马尔可夫假设，t+1 时的状态仅仅取决于 t 时的状态，既然一共有 N 种状态，那么从状态 Si 到状态 Sj 的概率就构成了一个 NN 的方阵，称为*状态转移矩阵 A：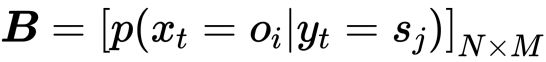

其中下标i、j分别表示状态的第i、j种取值，比如我们约定1表示标注集中的B，依序类推。 将状态转移概率矩阵的作用范围添加到示意图上，得到图4-9。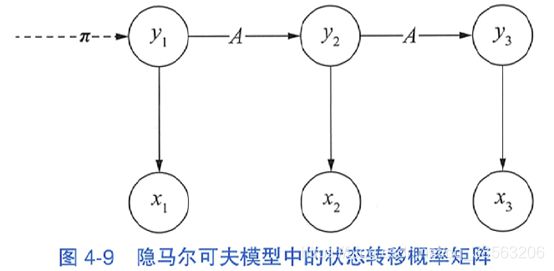图4-9隐马尔可夫模型中的状态转移概率矩阵

状态转移概率的存在有其实际意义，在中文分词中，标签 B 的后面不可能是 S，于是就有 P(Yt+1 = S | Yt = B) = 0就可以模拟这种禁止转移的需求。此外，汉语中的长词相对较少，于是隐马尔可夫模型可以通过较小的p(yt+1=M | yt=M)来模拟该语言现象。同样，词性标注中的“形容词->名词”“副词->动词”也可通过状态转移概率来模拟，这些概率分布参数不需要手动设置，而是通过语料库上的统计自动学习。

4.2.4 发射概率矩阵

有了状态 Yt 之后，如何确定观测 Xt 的概率分布呢？根据隐马尔可夫假设②，当前观测 Xt 仅仅取决于当前状态 Yt。也就是说，给定每种 y，x 都是一个独立的离散型随机变量，其参数对应一个向量。 假设观测 x 一共有 M 种可能的取值，则 x 的概率分布参数向量维度为 M。由于 y 共有 N 种，所以这些参数向量构成了 NM 的矩阵，称为*发射概率矩阵B。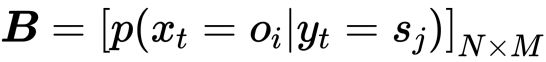

其中，第 i 行 j 列的元素下标 i 和 j 分别代表观测和状态的第 i 种和第 j 种取值，比如我们约定j = i表示字符集中的“阿”。此时p(x1=阿 | y1=B)对应矩阵中左上角第一个元素。如果字符集大小为1000的话，则B就是一个4×1000的矩阵。 将发射概率矩阵B的作用范围添加到示意图上，得到图4-10。图4-10隐马尔可夫模型中的发射概率矩阵 发射（emission）概率矩阵是一个非常形象的术语：将yt想象为不同的彩弹枪，xt想象为不同颜色的子弹，则根据yt确定xt的过程就像拔枪发射彩弹一样。不同的彩弹枪弹仓内的每种彩弹比例不同，导致有些彩弹枪更容易发射红色彩弹，另一些更容易发射绿色彩弹。 发射概率在中文分词中也具备实际意义，有些字符构词时的位置比较固定。比如作为词首的话（一把名为词首的彩弹枪），不容易观测到（发射出）“忑”，因为“忑”一般作为“忐忑”的词尾出现。通过赋予p(x1=忑 | y1=B）较低的概率，隐马尔可夫模型可以有效地防止“忐忑”被错误切开。 初始状态概率向量、状态转移概率矩阵与发射概率矩阵被称为隐马尔可夫模型的三元组λ=（π,A,B），只要三元组确定了，隐马尔可夫模型就确定了。有了隐马尔可夫模型之后，如何使用呢？

4.2.5. 隐马尔可夫模型的三个基本用法

隐马尔可夫模型的作用并不仅限于预测标注序列，它一共解决如下三个问题。

• 样本生成问题：给定模型，如何有效计算产生观测序列的概率？换言之，如何评估模型与观测序列之间的匹配程度？

• 序列预测问题：给定模型和观测序列，如何找到与此观测序列最匹配的状态序列？换言之，如何根据观测序列推断出隐藏的模型状态？

• 模型训练问题：给定观测序列，如何调整模型参数使得该序列出现的概率最大？换言之，如何训练模型使其能最好地描述观测数据？

前两个问题是模式识别的问题：1) 根据隐马尔科夫模型得到一个可观察状态序列的概率(评价)；2) 找到一个隐藏状态的序列使得这个序列产生一个可观察状态序列的概率最大(解码)。第三个问题就是根据一个可以观察到的状态序列集产生一个隐马尔科夫模型（学习）。

另一种解读：

（1）样本生成问题：给定模型λ=（π,A,B），生成满足模型约束的样本，即一系列观测序列及其对应的状态序列{(xi,yi)}。 （2）模型训练问题：给定训练集{(xi,yi)}，估计模型参数λ=（π,A,B）。 （3）序列预测问题：已知模型参数λ=（π,A,B），给定观测序列x，求最可能的状态序列y。 读者也许最关心第三个问题，但前两个问题也很重要。熟练掌握样本生成问题，可以巩固对隐马尔可夫模型的基本流程的理解，而模型训练更是直接关系到最后的预测问题。接下来的几个小节将同步介绍这些问题的解决原理与具体实现。

4.3 隐马尔可夫模型的样本生成

4.3.1 案例假设和模型构造

设想如下案例:某医院招标开发“智能”医疗诊断系统，用来辅助感冒诊断。已知①来诊者只有两种状态:要么健康，要么发烧。②来诊者不确定自己到底是哪种状态，只能回答感觉头晕、体寒或正常。医院认为，③感冒这种病，只跟病人前一天的状态有关，并且，④当天的病情决定当天的身体感觉。有位来诊者的病历卡上完整地记录了最近 T 天的身体感受(头晕、体寒或正常)，请预测这 T 天的身体状态(健康或发烧)。由于医疗数据属于机密隐私，医院无法提供训练数据，但根据医生经验，感冒发病的规律如下图4-11所示(箭头上的数值表示概率)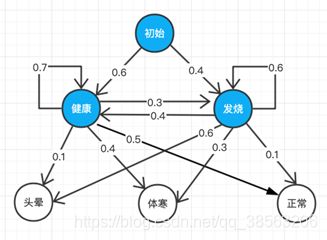：图4-11 病情-体感规律

从上往下看，一个人从初始状态出发，有0.4的概率进入发烧状态。发烧后的第二天有0.6的概率继续发烧，但发烧状态下也可能以0.1概率表现正常。要求设计算法，生成训练样本，作为下一阶段的测试数据。 根据已知条件①②，病情状态（健康、发烧）可作为隐马尔可夫模型的隐状态（图4-11中蓝色状态），而身体感受（头晕、体寒或正常）可作为隐马尔可夫模型的显状态（图中白色状态）。条件③符合隐马尔可夫模型假设一，条件④符合隐马尔可夫模型假设二。这个案例其实描述了一个隐马尔可夫模型，并且参数已经给定（参见图4-11）。其中，虚线对应初始状态概率向量，实线对应状态转移概率矩阵，加粗实线对应发射概率矩阵。