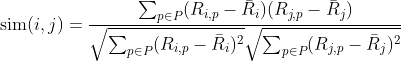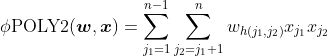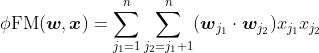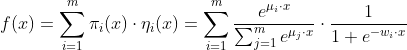《深度学习推荐系统》笔记（1）

目录

0 前言

1 互联网的增长引擎——推荐系统

2 前深度学习时代——推荐系统的进化之路

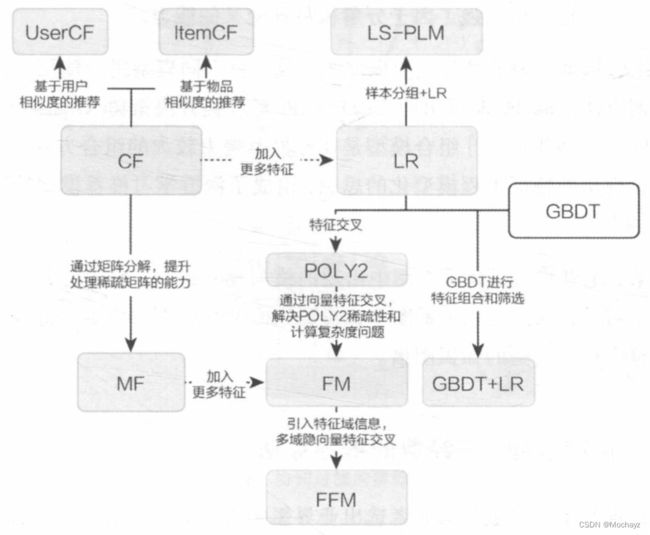
2.1 传统推荐模型的演化关系图

2.2 协同过滤——经典的推荐算法

UserCF

ItemCF

2.3 矩阵分解算法——协同过滤的进化

2.4 逻辑回归——融合多种特征的推荐模型

2.5 从FM到FFM——自动特征交叉的解决方案

POLY2模型——特征交叉的开始

FM模型——隐向量特征交叉

FFM模型——引入特征域的概念

2.6 GBDT+LR——特征工程模型化的开端

2.7 LS-PLM——阿里巴巴曾经的主流推荐系统

---

0 前言

工业界技术研发圈的方法体系：

        (1) 拿着锤子找钉子：跟踪最新的顶会论文或大公司技术博客，寻找创新点，拿到自己的场景试一试，靠撞大运拿结果。

        (2) 问题驱动：定义清楚问题，想清楚技术的需求，然后寻找或构思相应的技术工具。

1 互联网的增长引擎——推荐系统

推荐系统的作用和意义：

        (1) 用户角度：推荐系统解决在“信息过载”的情况下，用户如何高效获得感兴趣信息的问题。

        (2) 公司角度：推荐系统解决产品能够最大限度地吸引用户、留存用户、增加用户黏性、提高用户转化率的问题，从而达到公司商业目标连续增长的目的。

推荐系统要处理的问题：

        对于用户（user），在特定场景（context）下，针对海量的“物品”信息，构建一个函数，预测用户对特定候选物品（item）的喜好程度，再根据喜好程度对所有候选物品进行排序，生成推荐列表。

推荐系统的技术架构：

        (1) 数据和信息

        推荐系统的数据部分主要负责“用户”“物品”“场景”的信息收集与处理。“客户端及服务器端实时数据处理”“流处理平台准实时数据处理”“大数据平台离线数据处理”三种平台的实时性由强到弱，海量数据处理能力由弱到强。

        推荐系统的数据处理系统会将原始数据进一步加工，加工后的数据出口主要有三个：生成推荐模型所需的样本数据，用于算法模型的训练和评估；生成推荐模型服务（model serving）所需的“特征”，用于推荐系统的线上推断；生成系统监控、商业智能（Business Intelligence, BI）系统所需的统计型数据。

        (2) 算法和模型

        模型的结构一般由“召回层”“排序层”“ 补充策略与算法层”组成。

        召回层：一般利用高效的召回规则、算法或简单的模型，快速从海量的候选集中召回用户可能感兴趣的物品。

        排序层：利用排序模型对初筛的候选集进行静排序。

        补充策略与算法层：也被称为“再排序层”，可以在将推荐列表返回之前，为兼顾结果的“多样性”“流行度”“新鲜度”等指标，结合一些补充的策略和算法对推荐列表进行一定的调整，最终形成用户可见的推荐列表。

        在线环境进行模型服务之前，需要通过模型训练（model training）确定参数。可以根据训练环境将训练方法分为“离线训练”和“在线更新”。

        此外，推荐系统的模型部分提供了“离线评估”和“线上A/B测试”等多种评估模块，用得出的评估指标指导下一步的模型迭代优化。

2 前深度学习时代——推荐系统的进化之路

2.1 传统推荐模型的演化关系图

2.2 协同过滤——经典的推荐算法

        “协同过滤”就是协同大家的反馈、评价和意见一起对海量的信息进行过滤，从中筛选出目标用户可能感兴趣的信息的推荐过程。

协同过滤的特点：

        协同过滤是一个直观、可解释性强的模型，但推荐结果的头部效应较明显，处理稀疏向量的能力弱。为了解决上述问题，矩阵分解技术在协同过滤共现矩阵的基础上，使用更稠密的隐向量表示用户和物品，挖掘用户和物品的隐含兴趣和隐含特征。另外，为了引入用户特征、物品特征和上下文特征，推荐系统逐渐发展到以逻辑回归模型为核心的、能够综合不同类型特征的机器学习模型的道路上。

UserCF与ItemCF的应用场景：

        (1) UserCF具备更强的社交特性，适用于新闻推荐场景。

        (2) ItemCF更适用于兴趣变化较为稳定的应用，适用于电商、视频推荐等场景。

UserCF

基于用户的协同过滤算法步骤：

        (1) 找到和目标用户兴趣相似的用户集合。

        (2) 找到这个集合中的用户喜欢的，且目标用户没有听说过的物品推荐给目标用户。

用户相似度计算：

        (1) 余弦相似度

        (2) 皮尔逊相关系数

        其中，代表用户对物品的评分；代表用户对所有物品的平均评分，代表所有物品的集合。

        (3) 修正皮尔逊系数

        其中，代表物品得到所有评分的平均分。

最终结果的排序：

        在获得相似用户之后，利用用户相似度和相似用户的评价的加权平均获得目标用户的评价预测。

        其中，权重是用户和用户的相似度，是用户对物品的评分。

        在获得用户对不同物品的评价预测后，最终的推荐列表根据预测得分进行排序即可得到。

ItemCF

基于物品的协同过滤算法步骤：

        (1) 基于历史数据，构建以用户为行坐标，物品为列坐标的维的共现矩阵。

        (2) 计算共现矩阵两两列向量间的相似性（计算方式与用户相似度的计算方式相同），构建维的物品相似度矩阵。

        (3) 获得用户历史行为数据中的正反馈物品列表。

        (4) 利用物品相似度矩阵，针对目标用户历史行为中的正反馈物品，找出相似的个物品，组成相似物品集合。

        (5) 对相似物品集合中的物品，利用相似度分值进行排序，生成最终的推荐列表。如果一个物品与多个用户行为历史中的正反馈物品相似，那么该物品最终的相似度应该是多个相似度的累加。

        其中，是目标用户的正反馈物品集合，是物品与物品的物品相似度，是用户对物品的已有评分。

2.3 矩阵分解算法——协同过滤的进化

矩阵分解算法的原理：

        矩阵分解算法期望为每一个用户和物品生成一个隐向量，将用户和物品定位到隐向量的表示空间上，距离相近的用户和物品表明兴趣特点接近，在推荐过程中，就应该把距离相近的物品推荐给目标用户。

        用户和物品的隐向量是通过分解协同过滤生成的共现矩阵得到的。矩阵分解算法将维的共现矩阵分解为维的用户矩阵和维的物品矩阵相乘的形式。其中是隐向量的维度，影响隐向量的表达能力、泛化程度，和矩阵分解的求解复杂度。

        基于用户矩阵和物品矩阵，用户对物品的预估评分如下所示。

        其中是用户在用户矩阵中的对应行向量，是物品在物品矩阵中的对应列向量。

矩阵分解的求解过程：

        梯度下降法是进行矩阵分解的主要方法。为了让原始评分与用户向量和物品向量之积的差尽量小，最大限度地保存共现矩阵的原始信息，使用如下加入正则项的目标函数。

        对目标函数的求解可以利用非常标准的梯度下降过程完成：(1) 确定目标函数。(2) 对目标函数求偏导，求取梯度下降的方向和幅度。(3) 利用上一步的求导结果，沿梯度的反方向更新参数。(4) 当迭代次数超过上限或损失低于阈值时，结束训练，否则循环更新。

        隐向量的生成过程其实是对共现矩阵进行全局拟合的过程，因此有相较协同过滤有更强的泛化能力。

消除用户和物品打分的偏差：

        为了消除用户和物品打分的偏差，常用的做法是在矩阵分解时加入用户和物品的偏差向量。

        其中是全局偏差常数，是物品偏差系数，可使用物品收到的所有评分的均值，是用户偏差系数，可使用用户给出的所有评分的均值。矩阵分解目标函数相应地做出改变。

矩阵分解的优点和局限性：

        (1) 泛化能力强；空间复杂度低；更好的扩展性和灵活性。

        (2) 与协同过滤一样，矩阵分解不方便加入用户、物品和上下文相关的特征。

2.4 逻辑回归——融合多种特征的推荐模型

        相比协同过滤和矩阵分解利用用户和物品的“相似度”进行推荐，逻辑回归将推荐问题看成一个分类问题，通过预测正样本的概率对物品进行排序。

基于逻辑回归的推荐过程：

        (1) 将用户、物品和上下文特征转换成数值型特征向量。

        (2) 确定优化目标（以“点击率”为例），利用样本数据进行模型训练，确定模型参数。

        (3) 在模型服务阶段，将特征向量输入逻辑回归模型，经过推断得到用户“点击”物品的概率。

        (4) 利用“点击”概率对所有候选物品进行排序，得到推荐列表。

逻辑回归模型的推断过程：

        (1) 将特征向量作为模型的输入。

        (2) 通过为各特征赋予相应的权重并进行加权求和，得到。

        (3) 将输入sigmoid函数，使之映射到0~1的区间，得到最终的“点击率”。

逻辑回归模型的特点：

        (1) 数学含义上的支撑；可解释性强；工程化的需要。

        (2) 表达能力不强，无法进行特征交叉、特征筛选等一系列较为“高级”的操作。为解决这一问题，衍生出因子分解机等高维的复杂模型。在进入深度学习时代之后，多层神经网络可以完全替代逻辑回归模型。

2.5 从FM到FFM——自动特征交叉的解决方案

POLY2模型——特征交叉的开始

        POLY2模型对所有特征进行了两两交叉，并对所有的特征组合赋予权重。POLY2模型本质上仍是线性模型，便于工程上的兼容。

        POLY2模型存在两个较大的缺陷：在处理互联网数据时经常采用one-hot编码，POLY2将原本就非常稀疏的特征向量变得更稀疏；权重参数多，极大地增加了训练复杂度。

FM模型——隐向量特征交叉

        FM为每个特征学习了一个隐权重向量（latent vector）。在特征交叉时，使用两个特征隐向量的内积作为交叉特征的权重。

        FM极大地降低了训练开销，能更好地解决数据稀疏性的问题，且相比之后的深度学习模型更容易进行线上部署和服务。

FFM模型——引入特征域的概念

        相比FM模型，FFM模型引入了特征域感知（field-aware）这一概念，使模型的表达能力更强。每个特征对应的不是唯一一个隐向量，而是一组隐向量。当特征与特征进行交叉时，特征会从的这一组隐向量中挑出与特征的域对应的隐向量进行交叉，同理。

        FFM模型的表达能力更强，但计算复杂度上升，需要在模型效果和工程投入之间进行权衡。

2.6 GBDT+LR——特征工程模型化的开端

        Facebook提出了一种利用GBDT自动进行特征筛选和组合，进而生成新的离散特征向量，再把该特征向量当作LR模型输入，预估CTR的模型结构。GBDT是由多棵回归树组成的树林，后一棵树以前面树林的结果与真实结果的残差为拟合目标。回归树中每个节点的分裂是一个自然的特征选择过程，而多层节点的结构则对特征进行了有效的自动组合。

GBDT进行特征转换的过程：

        一个训练样本在输入GBDT的某一子树后，会根据每个节点的规则最终落入某一叶子节点，把该叶子节点置1，其他叶子节点置为0，所有叶子节点组成的向量即形成了该棵树的特征向量，把GBDT所有子树的特征向量连接起来，即形成了后续LR模型输入的离散型特征向量。

        事实上，决策树的深度决定了特征交叉的阶数，具备较强的特征组合能力。但GBDT容易过拟合，且特征转换方式实际上丢失了大量特征的数值信息。

        GBDT+LR组合模型的提出，意味着特征工程可以完全交由一个独立的模型来完成，实现真正的端到端（End to End）训练。广义上讲，深度学习模型通过各类网络结构、Embedding层等方法完成特征工程的自动化，都是GBDT+LR开启的特征工程模型化这一趋势的延续。

2.7 LS-PLM——阿里巴巴曾经的主流推荐系统

        LS-PLM（Large Scale Piece-wise Linear Linear Model），又被称为MLR（Mixed Logistic Regression）模型，在逻辑回归的基础上采用分而治之的思路，先对样本进行分片，再在样本分片中应用逻辑回归进行CTR预估。

        LS-PLM的数学形式如下所示，首先用聚类函数对样本进行分类（这里采用了softmax函数对样本进行多分类），再用LR模型计算样本在分片中具体的CTR，然后将二者相乘后求和。

        其中的超参数“分片数”可以较好地平衡模型的拟合与推广能力。

LS-PLM模型的特点：

        (1) 端到端的非线性学习能力；模型的稀疏性强（在建模时引入了L1和L2范数）。

        (2) 可以看作一个加入了注意力（Attention）机制的三层神经网络模型，其中输入层是样本的特征向量，中间层是由（分片的个数）个神经元组成的隐层，对于一个CTR预估问题，最后一层是由单一神经元组成的输出层。