Genlovy_Hoo大神的杰作

[转]支持向量机学习笔记

支持向量机学习笔记 呕心沥血整理的SVM学习笔记，完整总结了SVM的思想和整个求解过程，里面有诸多本人在学习过程中的想法，希望对初学者有帮助！ pdf下载地址：  http://download.csdn.net/detail/u013337691/9771283  链接：http://pan.baidu.com/s/1gfOKhrX 密码：12l9                                     作者：u013337691 发表于2017/3/5 23:31:26  原文链接 阅读：85 评论：0  查看评论

[原]混合灰狼优化（HGWO，DE-GWO）算法matlab源码

说明：博主所有博文及源码中示例所用的支持向量机算法均使用faruto改进的LIBSVM工具箱3.1版本，详细可参见faruto博客http://blog.sina.com.cn/u/1291365075以及http://www.matlabsky.com/thread-17936-1-1.html。 今天学习一个比较新的优化算法，用差分进化(DE)改进原始的灰狼优化（GWO）得到的HGWO（也可以叫DE-GWO）算法。仍然以优化SVR参数为例，需要的同学可以根据需要自己修改源码。 完整程序和示例文件地址：http://download.csdn.net/detail/u013337691/9675376  百度云链接: http://pan.baidu.com/s/1qYvVguS 密码: i7ie function [bestc,bestg,test_pre]=my_HGWO_SVR(para,input_train,output_train,input_test,output_test) % 参数向量 parameters [n,N_iteration,beta_min,beta_max,pCR] % n为种群规模，N_iteration为迭代次数 % beta_min 缩放因子下界 Lower Bound of Scaling Factor % beta_max=0.8; % 缩放因子上界 Upper Bound of Scaling Factor % pCR 交叉概率 Crossover Probability % 要求输入数据为列向量（矩阵） %% 数据归一化 [input_train,rule1]=mapminmax(input_train'); [output_train,rule2]=mapminmax(output_train'); input_test=mapminmax('apply',input_test',rule1); output_test=mapminmax('apply',output_test',rule2); input_train=input_train'; output_train=output_train'; input_test=input_test'; output_test=output_test'; %% 利用差分进化-灰狼优化混合算法（DE_GWO）选择最佳的SVR参数 nPop=para(1); % 种群规模 Population Size MaxIt=para(2); % 最大迭代次数Maximum Number of Iterations nVar=2; % 自变量维数，此例需要优化两个参数c和g Number of Decision Variables VarSize=[1,nVar]; % 决策变量矩阵大小 Decision Variables Matrix Size beta_min=para(3); % 缩放因子下界 Lower Bound of Scaling Factor beta_max=para(4); % 缩放因子上界 Upper Bound of Scaling Factor pCR=para(5); % 交叉概率 Crossover Probability lb=[0.01,0.01]; % 参数取值下界 ub=[100,100]; % 参数取值上界 %% 初始化 % 父代种群初始化 parent_Position=init_individual(lb,ub,nVar,nPop); % 随机初始化位置 parent_Val=zeros(nPop,1); % 目标函数值 for i=1:nPop % 遍历每个个体 parent_Val(i)=fobj(parent_Position(i,:),input_train,output_train,input_test,output_test); % 计算个体目标函数值 end % 突变种群初始化 mutant_Position=init_individual(lb,ub,nVar,nPop); % 随机初始化位置 mutant_Val=zeros(nPop,1); % 目标函数值 for i=1:nPop % 遍历每个个体 mutant_Val(i)=fobj(mutant_Position(i,:),input_train,output_train,input_test,output_test); % 计算个体目标函数值 end % 子代种群初始化 child_Position=init_individual(lb,ub,nVar,nPop); % 随机初始化位置 child_Val=zeros(nPop,1); % 目标函数值 for i=1:nPop % 遍历每个个体 child_Val(i)=fobj(child_Position(i,:),input_train,output_train,input_test,output_test); % 计算个体目标函数值 end %% 确定父代种群中的Alpha,Beta,Delta狼 [~,sort_index]=sort(parent_Val); % 父代种群目标函数值排序 parent_Alpha_Position=parent_Position(sort_index(1),:); % 确定父代Alpha狼 parent_Alpha_Val=parent_Val(sort_index(1)); % 父代Alpha狼目标函数值 parent_Beta_Position=parent_Position(sort_index(2),:); % 确定父代Beta狼 parent_Delta_Position=parent_Position(sort_index(3),:); % 确定父代Delta狼 %% 迭代开始 BestCost=zeros(1,MaxIt); BestCost(1)=parent_Alpha_Val; for it=1:MaxIt a=2-it*((2)/MaxIt); % 对每一次迭代，计算相应的a值，a decreases linearly fron 2 to 0 % 更新父代个体位置 for par=1:nPop % 遍历父代个体 for var=1:nVar % 遍历每个维度 % Alpha狼Hunting r1=rand(); % r1 is a random number in [0,1] r2=rand(); % r2 is a random number in [0,1] A1=2*a*r1-a; % 计算系数A C1=2*r2; % 计算系数C D_alpha=abs(C1*parent_Alpha_Position(var)-parent_Position(par,var)); X1=parent_Alpha_Position(var)-A1*D_alpha; % Beta狼Hunting r1=rand(); r2=rand(); A2=2*a*r1-a; % 计算系数A C2=2*r2; % 计算系数C D_beta=abs(C2*parent_Beta_Position(var)-parent_Position(par,var)); X2=parent_Beta_Position(var)-A2*D_beta; % Delta狼Hunting r1=rand(); r2=rand(); A3=2*a*r1-a; % 计算系数A C3=2*r2; % 计算系数C D_delta=abs(C3*parent_Delta_Position(var)-parent_Position(par,var)); X3=parent_Delta_Position(var)-A3*D_delta; % 位置更新，防止越界 X=(X1+X2+X3)/3; X=max(X,lb(var)); X=min(X,ub(var)); parent_Position(par,var)=X; end parent_Val(par)=fobj(parent_Position(par,:),input_train,output_train,input_test,output_test); % 计算个体目标函数值 end % 产生变异（中间体）种群 for mut=1:nPop A=randperm(nPop); % 个体顺序重新随机排列 A(A==i)=[]; % 当前个体所排位置腾空（产生变异中间体时当前个体不参与） a=A(1); b=A(2); c=A(3); beta=unifrnd(beta_min,beta_max,VarSize); % 随机产生缩放因子 y=parent_Position(a)+beta.*(parent_Position(b)-parent_Position(c)); % 产生中间体 % 防止中间体越界 y=max(y,lb); y=min(y,ub); mutant_Position(mut,:)=y; end % 产生子代种群，交叉操作 Crossover for child=1:nPop x=parent_Position(child,:); y=mutant_Position(child,:); z=zeros(size(x)); % 初始化一个新个体 j0=randi([1,numel(x)]); % 产生一个伪随机数，即选取待交换维度编号？？？ for var=1:numel(x) % 遍历每个维度 if var==j0 || rand<=pCR % 如果当前维度是待交换维度或者随机概率小于交叉概率 z(var)=y(var); % 新个体当前维度值等于中间体对应维度值 else z(var)=x(var); % 新个体当前维度值等于当前个体对应维度值 end end child_Position(child,:)=z; % 交叉操作之后得到新个体 child_Val(child)=fobj(z,input_train,output_train,input_test,output_test); % 新个体目标函数值 end % 父代种群更新 for par=1:nPop if child_Val(par)% 如果子代个体优于父代个体 parent_Val(par)=child_Val(par); % 更新父代个体 end end % 确定父代种群中的Alpha,Beta,Delta狼 [~,sort_index]=sort(parent_Val); % 父代种群目标函数值排序 parent_Alpha_Position=parent_Position(sort_index(1),:); % 确定父代Alpha狼 parent_Alpha_Val=parent_Val(sort_index(1)); % 父代Alpha狼目标函数值 parent_Beta_Position=parent_Position(sort_index(2),:); % 确定父代Beta狼 parent_Delta_Position=parent_Position(sort_index(3),:); % 确定父代Delta狼 BestCost(it)=parent_Alpha_Val; end bestc=parent_Alpha_Position(1,1); bestg=parent_Alpha_Position(1,2); %% 图示寻优过程 plot(BestCost); xlabel('Iteration'); ylabel('Best Val'); grid on; %% 利用回归预测分析最佳的参数进行SVM网络训练 cmd_cs_svr=['-s 3 -t 2',' -c ',num2str(bestc),' -g ',num2str(bestg)]; model_cs_svr=svmtrain(output_train,input_train,cmd_cs_svr); % SVM模型训练 %% SVM网络回归预测 [output_test_pre,~]=svmpredict(output_test,input_test,model_cs_svr); % SVM模型预测及其精度 test_pre=mapminmax('reverse',output_test_pre',rule2); test_pre = test_pre'; function x=init_individual(xlb,xub,dim,sizepop) % 参数初始化函数 % lb：参数下界，行向量 % ub：参数上界，行向量 % dim：参数维度 % sizepop 种群规模 % x：返回sizepop*size(lb,2)的参数矩阵 xRange=repmat((xub-xlb),[sizepop,1]); xLower=repmat(xlb,[sizepop,1]); x=rand(sizepop,dim).*xRange+xLower; %% SVR_fitness -- objective function function fitness=fobj(cv,input_train,output_train,input_test,output_test) % cv为长度为2的横向量，即SVR中参数c和v的值 cmd = ['-s 3 -t 2',' -c ',num2str(cv(1)),' -g ',num2str(cv(2))]; model=svmtrain(output_train,input_train,cmd); % SVM模型训练 [~,fitness]=svmpredict(output_test,input_test,model); % SVM模型预测及其精度 fitness=fitness(2); % 以平均均方误差MSE作为优化的目标函数值 clear clc close all load wndspd % 示例数据为风速（时间序列）数据，共144个样本 %% HGWO-SVR % 训练/测试数据准备（用前3天预测后一天）,用前100天做训练数据 input_train(1,:)=wndspd(1:97); input_train(2,:)=wndspd(2:98); input_train(3,:)=wndspd(3:99); output_train=[wndspd(4:100)]'; input_test(1,:)=wndspd(101:end-3); input_test(2,:)=wndspd(102:end-2); input_test(3,:)=wndspd(103:end-1); output_test=(wndspd(104:end))'; para=[30,500,0.2,0.8,0.2]; [bestc,bestg,test_pre]=my_HGWO_SVR(para,input_train',output_train',input_test',output_test'); %% 预测结果图 err_pre=output_test'-test_pre; figure('Name','测试数据残差图') set(gcf,'unit','centimeters','position',[0.5,5,30,5]) plot(err_pre,'*-'); figure('Name','原始-预测图') plot(test_pre,'*r-');hold on;plot(output_test,'bo-'); legend('预测','原始',0) set(gcf,'unit','centimeters','position',[0.5,13,30,5]) toc 参考文章：Aijun Zhu, Chuanpei Xu, Zhi Li, Jun Wu, and Zhenbing Liu. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC. Journal of Systems Engineering and Electronics Vol. 26, No. 2, April 2015, pp.317–328.  文章地址：http://ieeexplore.ieee.org/document/7111168/ （广告）欢迎扫描关注微信公众号：Genlovhyy的数据小站(Gnelovy212) 作者：u013337691 发表于2016/11/7 17:00:40  原文链接 阅读：970 评论：2  查看评论

[原]DE（差分进化）优化算法MATLAB源码详细中文注解

以优化SVR算法的参数c和g为例，对DE（差分进化）算法MATLAB源码进行了详细中文注解。  完整程序和示例文件地址：http://download.csdn.net/detail/u013337691/9671714  百度云链接: http://pan.baidu.com/s/1dEYAHS9 密码: 6xw5 function [bestc,bestg,test_pre]=my_DE_SVR(para,input_train,output_train,input_test,output_test) % 参数向量 parameters [n,N_iteration,beta_min,beta_max,pCR] % n为种群规模，N_iteration为迭代次数 % beta_min 缩放因子下界 Lower Bound of Scaling Factor % beta_max=0.8; % 缩放因子上界 Upper Bound of Scaling Factor % pCR 交叉概率 Crossover Probability % 要求输入数据为列向量（矩阵） %% 数据归一化 [input_train,rule1]=mapminmax(input_train'); [output_train,rule2]=mapminmax(output_train'); input_test=mapminmax('apply',input_test',rule1); output_test=mapminmax('apply',output_test',rule2); input_train=input_train'; output_train=output_train'; input_test=input_test'; output_test=output_test'; %% 利用差分进化（DE）算法选择最佳的SVR参数 nPop=para(1); % 种群规模 Population Size MaxIt=para(2); % 最大迭代次数Maximum Number of Iterations nVar=2; % 自变量维数，此例需要优化两个参数c和g Number of Decision Variables VarSize=[1,nVar]; % 决策变量矩阵大小 Decision Variables Matrix Size beta_min=para(3); % 缩放因子下界 Lower Bound of Scaling Factor beta_max=para(4); % 缩放因子上界 Upper Bound of Scaling Factor pCR=para(5); % 交叉概率 Crossover Probability lb=[0.01,0.01]; % 参数取值下界 ub=[100,100]; % 参数取值上界 %% 初始化 Initialization empty_individual.Position=[]; % 种群初始化 empty_individual.Cost=[]; % 种群目标函数值初始化 BestSol.Cost=inf; % 最优值初始化 pop=repmat(empty_individual,nPop,1); % 将保存种群信息的结构体扩展为结构体矩阵，行数等于种群大小 for i=1:nPop % 遍历每个个体 pop(i).Position=init_individual(lb,ub,nVar,1); % 随机初始化个体 pop(i).Cost=fobj(pop(i).Position,input_train,output_train,input_test,output_test); % 计算个体目标函数值 if pop(i).Cost<BestSol.Cost % 如果个体目标函数值优于当前最优值 BestSol=pop(i); % 更新最优值 end end BestCost=zeros(MaxIt,1); % 初始化迭代最优值 %% 主循环 DE Main Loop for it=1:MaxIt for i=1:nPop % 遍历每个个体 x=pop(i).Position; % 提取个体位置 % 随机选择三个个体以备变异使用 A=randperm(nPop); % 个体顺序重新随机排列 A(A==i)=[]; % 当前个体所排位置腾空（产生变异中间体时当前个体不参与） a=A(1); b=A(2); c=A(3); % 变异操作 Mutation beta=unifrnd(beta_min,beta_max,VarSize); % 随机产生缩放因子 y=pop(a).Position+beta.*(pop(b).Position-pop(c).Position); % 产生中间体 % 防止中间体越界 y=max(y,lb); y=min(y,ub); % 交叉操作 Crossover z=zeros(size(x)); % 初始化一个新个体 j0=randi([1,numel(x)]); % 产生一个伪随机数，即选取待交换维度编号？？？ for j=1:numel(x) % 遍历每个维度 if j==j0 || rand<=pCR % 如果当前维度是待交换维度或者随机概率小于交叉概率 z(j)=y(j); % 新个体当前维度值等于中间体对应维度值 else z(j)=x(j); % 新个体当前维度值等于当前个体对应维度值 end end NewSol.Position=z; % 交叉操作之后得到新个体 NewSol.Cost=fobj(NewSol.Position,input_train,output_train,input_test,output_test); % 新个体目标函数值 if NewSol.Costi).Cost % 如果新个体优于当前个体 pop(i)=NewSol; % 更新当前个体 if pop(i).Cost<BestSol.Cost % 如果当前个体（更新后的）优于最优个体 BestSol=pop(i); % 更新最优个体 end end end % 保存当前迭代最优个体函数值 Update Best Cost BestCost(it)=BestSol.Cost; end bestc=BestSol.Position(1,1); bestg=BestSol.Position(1,2); %% 图示寻优过程 plot(BestCost); xlabel('Iteration'); ylabel('Best Val'); grid on; %% 利用回归预测分析最佳的参数进行SVM网络训练 cmd_cs_svr=['-s 3 -t 2',' -c ',num2str(bestc),' -g ',num2str(bestg)]; model_cs_svr=svmtrain(output_train,input_train,cmd_cs_svr); % SVM模型训练 %% SVM网络回归预测 [output_test_pre,~]=svmpredict(output_test,input_test,model_cs_svr); % SVM模型预测及其精度 test_pre=mapminmax('reverse',output_test_pre',rule2); test_pre = test_pre'; %% SVR_fitness -- objective function function fitness=fobj(cv,input_train,output_train,input_test,output_test) % cv为长度为2的横向量，即SVR中参数c和v的值 cmd = ['-s 3 -t 2',' -c ',num2str(cv(1)),' -g ',num2str(cv(2))]; model=svmtrain(output_train,input_train,cmd); % SVM模型训练 [~,fitness]=svmpredict(output_test,input_test,model); % SVM模型预测及其精度 fitness=fitness(2); % 以平均均方误差MSE作为优化的目标函数值 function x=init_individual(xlb,xub,dim,sizepop) % 参数初始化函数 % lb：参数下界，行向量 % ub：参数上界，行向量 % dim：参数维度 % sizepop 种群规模 % x：返回sizepop*size(lb,2)的参数矩阵 xRange=repmat((xub-xlb),[sizepop,1]); xLower=repmat(xlb,[sizepop,1]); x=rand(sizepop,dim).*xRange+xLower; clear clc close all load wndspd % 示例数据为风速（时间序列）数据，共144个样本 %% PSO-SVR % 训练/测试数据准备（用前3天预测后一天）,用前100天做训练数据 input_train(1,:)=wndspd(1:97); input_train(2,:)=wndspd(2:98); input_train(3,:)=wndspd(3:99); output_train=[wndspd(4:100)]'; input_test(1,:)=wndspd(101:end-3); input_test(2,:)=wndspd(102:end-2); input_test(3,:)=wndspd(103:end-1); output_test=[wndspd(104:end)]'; para=[30,200,0.2,0.8,0.2]; [bestc,bestg,test_pre]=my_DE_SVR(para,input_train',output_train',input_test',output_test'); % 预测误差计算 MSE=mymse(output_test',test_pre) MAE=mymae(output_test',test_pre) MAPE=mymape(output_test',test_pre) FVD=myfvd(output_test',test_pre) CDFR=mycdfr(output_test',test_pre) %% 预测结果图 err_pre=output_test'-test_pre; figure('Name','测试数据残差图') set(gcf,'unit','centimeters','position',[0.5,5,30,5]) plot(err_pre,'*-'); figure('Name','原始-预测图') plot(test_pre,'*r-');hold on;plot(output_test,'bo-'); legend('预测','原始',0) set(gcf,'unit','centimeters','position',[0.5,13,30,5]) toc 本文参考：http://cn.mathworks.com/matlabcentral/fileexchange/52897-differential-evolution–de-?s_tid=srchtitle （广告）欢迎扫描关注微信公众号：Genlovhyy的数据小站(Gnelovy212)  作者：u013337691 发表于2016/11/3 10:18:45  原文链接 阅读：1290 评论：0  查看评论

[转]GSA（引力搜索）优化算法MATLAB源码详细中文注解

以优化SVM算法的参数c和g为例，对GSA（引力搜索）算法MATLAB源码进行了详细中文注解。  完整程序和示例文件地址：http://download.csdn.net/detail/u013337691/9645312 tic % 计时器 %% 清空环境变量 close all clear clc format compact %% 数据提取 % 载入测试数据wine,其中包含的数据为classnumber = 3,wine:178*13的矩阵,wine_labes:178*1的列向量 load wine.mat % 选定训练集和测试集 % 将第一类的1-30,第二类的60-95,第三类的131-153做为训练集 train_wine = [wine(1:30,:);wine(60:95,:);wine(131:153,:)]; % 相应的训练集的标签也要分离出来 train_wine_labels = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)]; % 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集 test_wine = [wine(31:59,:);wine(96:130,:);wine(154:178,:)]; % 相应的测试集的标签也要分离出来 test_wine_labels = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)]; %% 数据预处理 % 数据预处理,将训练集和测试集归一化到[0,1]区间 [mtrain,ntrain] = size(train_wine); [mtest,ntest] = size(test_wine); dataset = [train_wine;test_wine]; % mapminmax为MATLAB自带的归一化函数 [dataset_scale,ps] = mapminmax(dataset',0,1); dataset_scale = dataset_scale'; train_wine = dataset_scale(1:mtrain,:); test_wine = dataset_scale( (mtrain+1):(mtrain+mtest),: ); %% GSA优化参数 N=20; % 群体规模 Number of agents. max_it=30; % 最大迭代次数 Maximum number of iterations (T). ElitistCheck=1; % 如果ElitistCheck=1,则使用文献中的公式21；如果ElitistCheck=0，则用文献中的公式9. Rpower=1;% 文献中公式7中的R的幂次数 power of 'R' in eq.7. min_flag=1; % 取1求解极小值问题，取0求解极大值问题 1: minimization, 0: maximization. objfun=@objfun_svm; % 目标函数 [Fbest,Lbest,BestChart,MeanChart]=GSA_svm(objfun,N,max_it,ElitistCheck,min_flag,Rpower,... train_wine_labels,train_wine,test_wine_labels,test_wine); % Fbest: 最优目标值 Best result. % Lbest: 最优解 Best solution. The location of Fbest in search space. % BestChart: 最优解变化趋势 The best so far Chart over iterations. % MeanChart: 平均适应度函数值变化趋势 The average fitnesses Chart over iterations. %% 打印参数选择结果 bestc=Lbest(1); bestg=Lbest(2); disp('打印选择结果'); str=sprintf('Best c = %g，Best g = %g',bestc,bestg); disp(str) %% 利用最佳的参数进行SVM网络训练 cmd_gwosvm = ['-c ',num2str(bestc),' -g ',num2str(bestg)]; model_gwosvm = svmtrain(train_wine_labels,train_wine,cmd_gwosvm); %% SVM网络预测 [predict_label,accuracy] = svmpredict(test_wine_labels,test_wine,model_gwosvm); % 打印测试集分类准确率 total = length(test_wine_labels); right = sum(predict_label == test_wine_labels); disp('打印测试集分类准确率'); str = sprintf( 'Accuracy = %g%% (%d/%d)',accuracy(1),right,total); disp(str); %% 结果分析 % 测试集的实际分类和预测分类图 figure; hold on; plot(test_wine_labels,'o'); plot(predict_label,'r*'); xlabel('测试集样本','FontSize',12); ylabel('类别标签','FontSize',12); legend('实际测试集分类','预测测试集分类'); title('测试集的实际分类和预测分类图','FontSize',12); grid on %% 最优适应度变化曲线 figure('Name','最优适应度变化曲线') plot(BestChart,'--k'); title('最优适应度变化曲线'); xlabel('\fontsize{12}\bf Iteration');ylabel('\fontsize{12}\bf Best-so-far'); legend('\fontsize{10}\bf GSA',1); %% 显示程序运行时间 toc function [Fbest,Lbest,BestChart,MeanChart]=GSA_svm(objfun,N,max_it,ElitistCheck,min_flag,Rpower,... train_wine_labels,train_wine,test_wine_labels,test_wine) % 说明 % Main function for Gravitational Search Algorithm. % V: 速度 Velocity. % a: 加速度 Acceleration. % M: 惯性质量 Mass. Ma=Mp=Mi=M; % dim: 自变量维度 Dimension of the test function. % N: 种群规模 Number of agents. % X: 个体位置集，一个N*dim矩阵 Position of agents. dim-by-N matrix. % R: 个体距离 Distance between agents in search space. % [low-up]: 参数范围 Allowable range for search space. % Rnorm: 范数，参考文献公式8 Norm in eq.8. % Rpower: 参考文献公式7 Power of R in eq.7. Rnorm=2; % 使用二阶范数 % 获取目标函数参数界限、维数 get allowable range and dimension of the test function. low=0.01; up=100; dim=2; % 随机初始化种群 random initialization for agents. X=initialization(dim,N,up,low); % 用于保存当前最优值和平均适应度值变化情况 create the best so far chart and average fitnesses chart. BestChart=zeros(1,max_it); MeanChart=zeros(1,max_it); % 初始化个体解 V=zeros(N,dim); for iteration=1:max_it % 检查是否越界 Checking allowable range. X=space_bound(X,up,low); % 计算个体适应度函数值 Evaluation of agents. fitness=zeros(1,N); for agent=1:N fitness(1,agent)=objfun(X(agent,:),train_wine_labels,train_wine,test_wine_labels,test_wine); end % 寻找当前迭代最优个体 if min_flag==1 [best,best_X]=min(fitness); % 最小化情况 minimization. else [best,best_X]=max(fitness); % 最大化情况 maximization. end if iteration==1 Fbest=best; Lbest=X(best_X,:); end % 更新目前为止最优个体 if min_flag==1 if best% 最小化情况 minimization. Fbest=best; Lbest=X(best_X,:); end else if best>Fbest % 最大化情况 maximization Fbest=best; Lbest=X(best_X,:); end end BestChart(iteration)=Fbest; MeanChart(iteration)=mean(fitness); % 计算惯性质量M（文献公式14—20） Calculation of M. eq.14-20 M=massCalculation(fitness,min_flag); % 计算引力常亮（文献公式13） Calculation of Gravitational constant. eq.13. G=Gconstant(iteration,max_it); % 计算加速度 Calculation of accelaration in gravitational field. eq.7-10,21. a=Gfield(M,X,G,Rnorm,Rpower,ElitistCheck,iteration,max_it); % 个体移动 Agent movement. eq.11-12 [X,V]=move(X,a,V); end % This function initializes the position of the agents in the search space, randomly. function X=initialization(dim,N,up,down) if size(up,2)==1 X=rand(N,dim).*(up-down)+down; end if size(up,2)>1 for i=1:dim high=up(i); low=down(i); X(:,i)=rand(N,1).*(high-low)+low; end end % This function calculates the mass of each agent. eq.14-20 function M =massCalculation(fit,min_flag) % Here, make your own function of 'mass calculation' Fmax=max(fit); Fmin=min(fit); [~,N]=size(fit); if Fmax==Fmin M=ones(N,1); else if min_flag==1 % for minimization best=Fmin; worst=Fmax; % eq.17-18. else % for maximization best=Fmax; worst=Fmin; % eq.19-20. end M=(fit-worst)./(best-worst); % eq.15. end M=M./sum(M); % eq.16. % This function calculates Gravitational constant. eq.13. function G=Gconstant(iteration,max_it) % here, make your own function of 'G'. alfa=20; G0=100; G=G0*exp(-alfa*iteration/max_it); % eq.28. % This function calculates the accelaration of each agent in gravitational field. eq.7-10,21. function a=Gfield(M,X,G,Rnorm,Rpower,ElitistCheck,iteration,max_it) [N,dim]=size(X); % In the last iteration, only 2 percent of agents apply force to the others. % 在最后一次迭代中，只有百分之二的个体对其它个体有引力？？？ final_per=2; % 计算总引力 total force calculation if ElitistCheck==1 kbest=final_per+(1-iteration/max_it)*(100-final_per); % 参考文献公式21中kbest的计算 kbest in eq.21. kbest=round(N*kbest/100); else kbest=N; % eq.9. end [~,ds]=sort(M,'descend'); E=zeros(N,dim); for i=1:N % 遍历种群 E(i,:)=zeros(1,dim); for ii=1:kbest j=ds(ii); if j~=i R=norm(X(i,:)-X(j,:),Rnorm); % 欧氏距离 Euclidian distanse. for k=1:dim E(i,k)=E(i,k)+rand*(M(j))*((X(j,k)-X(i,k))/(R^Rpower+eps)); % note that Mp(i)/Mi(i)=1 end end end end % 加速度 acceleration a=E.*G; % note that Mp(i)/Mi(i)=1 % This function updates the velocity and position of agents. function [X,V]=move(X,a,V) % movement. [N,dim]=size(X); V=rand(N,dim).*V+a; % eq.11. X=X+V; % eq.12. % This function checks the search space boundaries for agents. function X=space_bound(X,up,low) [N,dim]=size(X); for i=1:N % 对越界值进行重新初始化 Agents that go out of the search space, are reinitialized randomly. Tp=X(i,:)>up; Tm=X(i,:)i,:)=(X(i,:).*(~(Tp+Tm)))+((rand(1,dim).*(up-low)+low).*logical((Tp+Tm))); % 将越界值重置为边界值 Agents that go out of the search space, are returned to the boundaries. % Tp=X(i,:)>up; % Tm=X(i,:) % X(i,:)=(X(i,:).*(~(Tp+Tm)))+up.*Tp+low.*Tm; end %% SVM_Objective Function function f=objfun_svm(cv,train_wine_labels,train_wine,test_wine_labels,test_wine) % cv为长度为2的横向量，即SVM中参数c和v的值 cmd = [' -c ',num2str(cv(1)),' -g ',num2str(cv(2))]; model=svmtrain(train_wine_labels,train_wine,cmd); % SVM模型训练 [~,fitness]=svmpredict(test_wine_labels,test_wine,model); % SVM模型预测及其精度 f=1-fitness(1)/100; % 以分类预测错误率作为优化的目标函数值 参考文献：E. Rashedi, H. Nezamabadi-pour and S. Saryazdi,  GSA: A Gravitational Search Algorithm，Information sciences, vol. 179，no. 13, pp. 2232-2248, 2009. （广告）欢迎扫描关注微信公众号：Genlovhyy的数据小站(Gnelovy212) 作者：u013337691 发表于2016/10/4 9:17:38  原文链接 阅读：960 评论：0  查看评论

[原]SA（模拟退火）优化算法MATLAB源码详细中文注解

以优化SVM算法的参数c和g为例，对SA（模拟退火）算法MATLAB源码进行了逐行中文注解。  完整程序和示例文件地址：http://download.csdn.net/detail/u013337691/9644107  链接：http://pan.baidu.com/s/1i5G0gPB 密码：4ge8 % 使用模拟退火法寻优SVM中的参数c和g % 使用METROPOLIS接受准则 %% 清空环境 tic % 计时 clear clc close all format compact %% 数据提取 % 载入测试数据wine,其中包含的数据为classnumber = 3,wine:178*13的矩阵,wine_labes:178*1的列向量 load wine.mat % 选定训练集和测试集 % 将第一类的1-30,第二类的60-95,第三类的131-153做为训练集 train_wine = [wine(1:30,:);wine(60:95,:);wine(131:153,:)]; % 相应的训练集的标签也要分离出来 train_wine_labels = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)]; % 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集 test_wine = [wine(31:59,:);wine(96:130,:);wine(154:178,:)]; % 相应的测试集的标签也要分离出来 test_wine_labels = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)]; %% 数据预处理 % 数据预处理,将训练集和测试集归一化到[0,1]区间 [mtrain,ntrain] = size(train_wine); [mtest,ntest] = size(test_wine); dataset = [train_wine;test_wine]; % mapminmax为MATLAB自带的归一化函数 [dataset_scale,ps] = mapminmax(dataset',0,1); dataset_scale = dataset_scale'; train_wine = dataset_scale(1:mtrain,:); test_wine = dataset_scale( (mtrain+1):(mtrain+mtest),: ); %% SA算法主程序 lb=[0.01,0.01]; % 参数取值下界 ub=[100,100]; % 参数取值上界 % 冷却表参数 MarkovLength=100; % 马可夫链长度 DecayScale=0.85; % 衰减参数 StepFactor=0.2; % Metropolis步长因子 Temperature0=8; % 初始温度 Temperatureend=3; % 最终温度 Boltzmann_con=1; % Boltzmann常数 AcceptPoints=0.0; % Metropolis过程中总接受点 % 随机初始化参数 range=ub-lb; Par_cur=rand(size(lb)).*range+lb; % 用Par_cur表示当前解 Par_best_cur=Par_cur; % 用Par_best_cur表示当前最优解 Par_best=rand(size(lb)).*range+lb; % 用Par_best表示冷却中的最好解 % 每迭代一次退火(降温)一次，直到满足迭代条件为止 t=Temperature0; itr_num=0; % 记录迭代次数 while t>Temperatureend itr_num=itr_num+1; t=DecayScale*t; % 温度更新（降温) for i=1:MarkovLength % 在此当前参数点附近随机选下一点 p=0; while p==0 Par_new=Par_cur+StepFactor.*range.*(rand(size(lb))-0.5); % 防止越界 if sum(Par_new>ub)+sum(Par_new0 p=1; end end % 检验当前解是否为全局最优解 if (objfun_svm(Par_best,train_wine_labels,train_wine,test_wine_labels,test_wine)>... objfun_svm(Par_new,train_wine_labels,train_wine,test_wine_labels,test_wine)) % 保留上一个最优解 Par_best_cur=Par_best; % 此为新的最优解 Par_best=Par_new; end % Metropolis过程 if (objfun_svm(Par_cur,train_wine_labels,train_wine,test_wine_labels,test_wine)-... objfun_svm(Par_new,train_wine_labels,train_wine,test_wine_labels,test_wine)>0) % 接受新解 Par_cur=Par_new; AcceptPoints=AcceptPoints+1; else changer=-1*(objfun_svm(Par_new,train_wine_labels,train_wine,test_wine_labels,test_wine)... -objfun_svm(Par_cur,train_wine_labels,train_wine,test_wine_labels,test_wine))/Boltzmann_con*Temperature0; p1=exp(changer); if p1>rand Par_cur=Par_new; AcceptPoints=AcceptPoints+1; end end end end %% 结果显示 disp(['最小值在点:',num2str(Par_best)]); Objval_best= objfun_svm(Par_best,train_wine_labels,train_wine,test_wine_labels,test_wine); disp(['最小值为:',num2str(Objval_best)]); %% 显示运行时间 toc %% SVM_Objective Function function f=objfun_svm(cv,train_wine_labels,train_wine,test_wine_labels,test_wine) % cv为长度为2的横向量，即SVM中参数c和v的值 cmd = [' -c ',num2str(cv(1)),' -g ',num2str(cv(2))]; model=svmtrain(train_wine_labels,train_wine,cmd); % SVM模型训练 [~,fitness]=svmpredict(test_wine_labels,test_wine,model); % SVM模型预测及其精度 f=1-fitness(1)/100; % 以分类预测错误率作为优化的目标函数值 （广告）欢迎扫描关注微信公众号：Genlovhyy的数据小站(Gnelovy212) 作者：u013337691 发表于2016/9/30 16:24:18  原文链接 阅读：164 评论：0  查看评论

[原]FA（萤火虫算法）MATLAB源码详细中文注解

以优化SVM算法的参数c和g为例，对FA（萤火虫算法）MATLAB源码进行了逐行中文注解。  完整程序和示例文件地址：http://download.csdn.net/detail/u013337691/9626263  链接：http://pan.baidu.com/s/1kVbd5cV 密码：7ym8 tic % 计时器 %% 清空环境变量 close all clear clc format compact %% 数据提取 % 载入测试数据wine,其中包含的数据为classnumber = 3,wine:178*13的矩阵,wine_labes:178*1的列向量 load wine.mat % 选定训练集和测试集 % 将第一类的1-30,第二类的60-95,第三类的131-153做为训练集 train_wine = [wine(1:30,:);wine(60:95,:);wine(131:153,:)]; % 相应的训练集的标签也要分离出来 train_wine_labels = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)]; % 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集 test_wine = [wine(31:59,:);wine(96:130,:);wine(154:178,:)]; % 相应的测试集的标签也要分离出来 test_wine_labels = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)]; %% 数据预处理 % 数据预处理,将训练集和测试集归一化到[0,1]区间 [mtrain,ntrain] = size(train_wine); [mtest,ntest] = size(test_wine); dataset = [train_wine;test_wine]; % mapminmax为MATLAB自带的归一化函数 [dataset_scale,ps] = mapminmax(dataset',0,1); dataset_scale = dataset_scale'; train_wine = dataset_scale(1:mtrain,:); test_wine = dataset_scale( (mtrain+1):(mtrain+mtest),: ); %% FA优化参数 % 参数向量 parameters [n N_iteration alpha betamin gamma] % n为种群规模，N_iteration为迭代次数 para=[10,50,0.5,0.2,1]; % 待优化参数上下界 Simple bounds/limits for d-dimensional problems d=2; % 待优化参数个数 Lb=[0.01,0.01]; % 下界 Ub=[100,100]; % 上界 % 参数初始化 Initial random guess u0=Lb+(Ub-Lb).*rand(1,d); % 迭代寻优 Display results [bestsolutio,bestojb]=ffa_mincon_svm(@objfun_svm,u0,Lb,Ub,para,train_wine_labels,train_wine,test_wine_labels,test_wine); %% 打印参数选择结果 bestc=bestsolutio(1); bestg=bestsolutio(2); disp('打印选择结果'); str=sprintf('Best c = %g，Best g = %g',bestc,bestg); disp(str) %% 利用最佳的参数进行SVM网络训练 cmd_gwosvm = ['-c ',num2str(bestc),' -g ',num2str(bestg)]; model_gwosvm = svmtrain(train_wine_labels,train_wine,cmd_gwosvm); %% SVM网络预测 [predict_label,accuracy] = svmpredict(test_wine_labels,test_wine,model_gwosvm); % 打印测试集分类准确率 total = length(test_wine_labels); right = sum(predict_label == test_wine_labels); disp('打印测试集分类准确率'); str = sprintf( 'Accuracy = %g%% (%d/%d)',accuracy(1),right,total); disp(str); %% 结果分析 % 测试集的实际分类和预测分类图 figure; hold on; plot(test_wine_labels,'o'); plot(predict_label,'r*'); xlabel('测试集样本','FontSize',12); ylabel('类别标签','FontSize',12); legend('实际测试集分类','预测测试集分类'); title('测试集的实际分类和预测分类图','FontSize',12); grid on %% 显示程序运行时间 toc % 萤火虫算法主程序开始 Start FA function [nbest,fbest]=ffa_mincon_svm(costfhandle,u0, Lb, Ub, para,train_wine_labels,train_wine,test_wine_labels,test_wine) % 检查输入参数 Check input parameters (otherwise set as default values) if nargin<5 para=[20 100 0.25 0.20 1]; end if nargin<4 Ub=[]; end if nargin<3 Lb=[]; end if nargin<2 disp('Usuage: FA_mincon(@cost,u0,Lb,Ub,para)'); end % n=number of fireflies % MaxGeneration=number of pseudo time steps % ------------------------------------------------ % alpha=0.25; % Randomness 0--1 (highly random) % betamn=0.20; % minimum value of beta % gamma=1; % Absorption coefficient % ------------------------------------------------ n=para(1); MaxGeneration=para(2); alpha=para(3); betamin=para(4); gamma=para(5); % 检查上界向量与下界向量长度是否相同 Check if the upper bound & lower bound are the same size if length(Lb) ~=length(Ub) disp('Simple bounds/limits are improper!') return end % 计算待优化参数维度 Calcualte dimension d=length(u0); % 初始化目标函数值 Initial values of an array zn=ones(n,1)*10^100; % ------------------------------------------------ % 初始化萤火虫位置 generating the initial locations of n fireflies [ns,Lightn]=init_ffa(n,d,Lb,Ub,u0); for k=1:MaxGeneration % 迭代开始 % 更新alpha（可选）This line of reducing alpha is optional alpha=alpha_new(alpha,MaxGeneration); % 对每个萤火虫计算目标函数值 Evaluate new solutions (for all n fireflies) for i=1:n zn(i)=costfhandle(ns(i,:),train_wine_labels,train_wine,test_wine_labels,test_wine); Lightn(i)=zn(i); end % 根据亮度排序 Ranking fireflies by their light intensity/objectives [Lightn,Index]=sort(zn); ns_tmp=ns; for i=1:n ns(i,:)=ns_tmp(Index(i),:); end %% 找出当前最优 Find the current best nso=ns; Lighto=Lightn; nbest=ns(1,:); Lightbest=Lightn(1); % 另存最优值 For output only fbest=Lightbest; % 向较优方向移动 Move all fireflies to the better locations [ns]=ffa_move(n,d,ns,Lightn,nso,Lighto,alpha,betamin,gamma,Lb,Ub); end % ----- All the subfunctions are listed here ------------ % 初始化萤火虫位置 The initial locations of n fireflies function [ns,Lightn]=init_ffa(n,d,Lb,Ub,u0) ns=zeros(n,d); if ~isempty(Lb) % 如果参数界限不为空 if there are bounds/limits for i=1:n ns(i,:)=Lb+(Ub-Lb).*rand(1,d); % 则在取值范围内随机取值 end else % 如果没有设置参数界限 for i=1:n ns(i,:)=u0+randn(1,d); % 在原有参数上加白噪声 end end % 初始化目标函数 initial value before function evaluations Lightn=ones(n,1)*10^100; % Move all fireflies toward brighter ones function [ns]=ffa_move(n,d,ns,Lightn,nso,Lighto,alpha,betamin,gamma,Lb,Ub) % 参数取值范围绝对值 Scaling of the system scale=abs(Ub-Lb); % 更新萤火虫 Updating fireflies for i=1:n % The attractiveness parameter beta=exp(-gamma*r) for j=1:n r=sqrt(sum((ns(i,:)-ns(j,:)).^2)); % Update moves if Lightn(i)>Lighto(j) % 如果i比j亮度更强 Brighter and more attractive beta0=1; beta=(beta0-betamin)*exp(-gamma*r.^2)+betamin; tmpf=alpha.*(rand(1,d)-0.5).*scale; ns(i,:)=ns(i,:).*(1-beta)+nso(j,:).*beta+tmpf; end end % end for j end % end for i % 防止越界 Check if the updated solutions/locations are within limits [ns]=findlimits(n,ns,Lb,Ub); % This function is optional, as it is not in the original FA % The idea to reduce randomness is to increase the convergence, % however, if you reduce randomness too quickly, then premature % convergence can occur. So use with care. % alpha参数更新函数 function alpha=alpha_new(alpha,NGen) % alpha_n=alpha_0(1-delta)^NGen=10^(-4); % alpha_0=0.9 delta=1-(10^(-4)/0.9)^(1/NGen); alpha=(1-delta)*alpha; % 防止越界 Make sure the fireflies are within the bounds/limits function [ns]=findlimits(n,ns,Lb,Ub) for i=1:n % Apply the lower bound ns_tmp=ns(i,:); I=ns_tmp% Apply the upper bounds J=ns_tmp>Ub; ns_tmp(J)=Ub(J); % Update this new move ns(i,:)=ns_tmp; end %% SVM_Objective Function function f=objfun_svm(cv,train_wine_labels,train_wine,test_wine_labels,test_wine) % cv为长度为2的横向量，即SVM中参数c和v的值 cmd = [' -c ',num2str(cv(1)),' -g ',num2str(cv(2))]; model=svmtrain(train_wine_labels,train_wine,cmd); % SVM模型训练 [~,fitness]=svmpredict(test_wine_labels,test_wine,model); % SVM模型预测及其精度 f=1-fitness(1)/100; % 以分类预测错误率作为优化的目标函数值 （广告）欢迎扫描关注微信公众号：Genlovhyy的数据小站(Gnelovy212) 作者：u013337691 发表于2016/9/9 15:13:27  原文链接 阅读：330 评论：0  查看评论

[原]GWO（灰狼优化）算法MATLAB源码逐行中文注解

以优化SVM算法的参数c和g为例，对GWO算法MATLAB源码进行了逐行中文注解。  完整程序和示例文件地址：http://download.csdn.net/detail/u013337691/9624866  链接：http://pan.baidu.com/s/1hrCheBE 密码：4p6m tic % 计时器 %% 清空环境变量 close all clear clc format compact %% 数据提取 % 载入测试数据wine,其中包含的数据为classnumber = 3,wine:178*13的矩阵,wine_labes:178*1的列向量 load wine.mat % 选定训练集和测试集 % 将第一类的1-30,第二类的60-95,第三类的131-153做为训练集 train_wine = [wine(1:30,:);wine(60:95,:);wine(131:153,:)]; % 相应的训练集的标签也要分离出来 train_wine_labels = [wine_labels(1:30);wine_labels(60:95);wine_labels(131:153)]; % 将第一类的31-59,第二类的96-130,第三类的154-178做为测试集 test_wine = [wine(31:59,:);wine(96:130,:);wine(154:178,:)]; % 相应的测试集的标签也要分离出来 test_wine_labels = [wine_labels(31:59);wine_labels(96:130);wine_labels(154:178)]; %% 数据预处理 % 数据预处理,将训练集和测试集归一化到[0,1]区间 [mtrain,ntrain] = size(train_wine); [mtest,ntest] = size(test_wine); dataset = [train_wine;test_wine]; % mapminmax为MATLAB自带的归一化函数 [dataset_scale,ps] = mapminmax(dataset',0,1); dataset_scale = dataset_scale'; train_wine = dataset_scale(1:mtrain,:); test_wine = dataset_scale( (mtrain+1):(mtrain+mtest),: ); %% 利用灰狼算法选择最佳的SVM参数c和g SearchAgents_no=10; % 狼群数量，Number of search agents Max_iteration=10; % 最大迭代次数，Maximum numbef of iterations dim=2; % 此例需要优化两个参数c和g，number of your variables lb=[0.01,0.01]; % 参数取值下界 ub=[100,100]; % 参数取值上界 % v = 5; % SVM Cross Validation参数,默认为5 % initialize alpha, beta, and delta_pos Alpha_pos=zeros(1,dim); % 初始化Alpha狼的位置 Alpha_score=inf; % 初始化Alpha狼的目标函数值，change this to -inf for maximization problems Beta_pos=zeros(1,dim); % 初始化Beta狼的位置 Beta_score=inf; % 初始化Beta狼的目标函数值，change this to -inf for maximization problems Delta_pos=zeros(1,dim); % 初始化Delta狼的位置 Delta_score=inf; % 初始化Delta狼的目标函数值，change this to -inf for maximization problems %Initialize the positions of search agents Positions=initialization(SearchAgents_no,dim,ub,lb); Convergence_curve=zeros(1,Max_iteration); l=0; % Loop counter循环计数器 % Main loop主循环 while l% 对迭代次数循环 for i=1:size(Positions,1) % 遍历每个狼 % Return back the search agents that go beyond the boundaries of the search space % 若搜索位置超过了搜索空间，需要重新回到搜索空间 Flag4ub=Positions(i,:)>ub; Flag4lb=Positions(i,:)% 若狼的位置在最大值和最小值之间，则位置不需要调整，若超出最大值，最回到最大值边界； % 若超出最小值，最回答最小值边界 Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb; % ~表示取反 % 计算适应度函数值 cmd = [' -c ',num2str(Positions(i,1)),' -g ',num2str(Positions(i,2))]; model=svmtrain(train_wine_labels,train_wine,cmd); % SVM模型训练 [~,fitness]=svmpredict(test_wine_labels,test_wine,model); % SVM模型预测及其精度 fitness=100-fitness(1); % 以错误率最小化为目标 % Update Alpha, Beta, and Delta if fitness% 如果目标函数值小于Alpha狼的目标函数值 Alpha_score=fitness; % 则将Alpha狼的目标函数值更新为最优目标函数值，Update alpha Alpha_pos=Positions(i,:); % 同时将Alpha狼的位置更新为最优位置 end if fitness>Alpha_score && fitness% 如果目标函数值介于于Alpha狼和Beta狼的目标函数值之间 Beta_score=fitness; % 则将Beta狼的目标函数值更新为最优目标函数值，Update beta Beta_pos=Positions(i,:); % 同时更新Beta狼的位置 end if fitness>Alpha_score && fitness>Beta_score && fitness% 如果目标函数值介于于Beta狼和Delta狼的目标函数值之间 Delta_score=fitness; % 则将Delta狼的目标函数值更新为最优目标函数值，Update delta Delta_pos=Positions(i,:); % 同时更新Delta狼的位置 end end a=2-l*((2)/Max_iteration); % 对每一次迭代，计算相应的a值，a decreases linearly fron 2 to 0 % Update the Position of search agents including omegas for i=1:size(Positions,1) % 遍历每个狼 for j=1:size(Positions,2) % 遍历每个维度 % 包围猎物，位置更新 r1=rand(); % r1 is a random number in [0,1] r2=rand(); % r2 is a random number in [0,1] A1=2*a*r1-a; % 计算系数A，Equation (3.3) C1=2*r2; % 计算系数C，Equation (3.4) % Alpha狼位置更新 D_alpha=abs(C1*Alpha_pos(j)-Positions(i,j)); % Equation (3.5)-part 1 X1=Alpha_pos(j)-A1*D_alpha; % Equation (3.6)-part 1 r1=rand(); r2=rand(); A2=2*a*r1-a; % 计算系数A，Equation (3.3) C2=2*r2; % 计算系数C，Equation (3.4) % Beta狼位置更新 D_beta=abs(C2*Beta_pos(j)-Positions(i,j)); % Equation (3.5)-part 2 X2=Beta_pos(j)-A2*D_beta; % Equation (3.6)-part 2 r1=rand(); r2=rand(); A3=2*a*r1-a; % 计算系数A，Equation (3.3) C3=2*r2; % 计算系数C，Equation (3.4) % Delta狼位置更新 D_delta=abs(C3*Delta_pos(j)-Positions(i,j)); % Equation (3.5)-part 3 X3=Delta_pos(j)-A3*D_delta; % Equation (3.5)-part 3 % 位置更新 Positions(i,j)=(X1+X2+X3)/3;% Equation (3.7) end end l=l+1; Convergence_curve(l)=Alpha_score; end bestc=Alpha_pos(1,1); bestg=Alpha_pos(1,2); bestGWOaccuarcy=Alpha_score; %% 打印参数选择结果 disp('打印选择结果'); str=sprintf('Best Cross Validation Accuracy = %g%%，Best c = %g，Best g = %g',bestGWOaccuarcy*100,bestc,bestg); disp(str) %% 利用最佳的参数进行SVM网络训练 cmd_gwosvm = ['-c ',num2str(bestc),' -g ',num2str(bestg)]; model_gwosvm = svmtrain(train_wine_labels,train_wine,cmd_gwosvm); %% SVM网络预测 [predict_label,accuracy] = svmpredict(test_wine_labels,test_wine,model_gwosvm); % 打印测试集分类准确率 total = length(test_wine_labels); right = sum(predict_label == test_wine_labels); disp('打印测试集分类准确率'); str = sprintf( 'Accuracy = %g%% (%d/%d)',accuracy(1),right,total); disp(str); %% 结果分析 % 测试集的实际分类和预测分类图 figure; hold on; plot(test_wine_labels,'o'); plot(predict_label,'r*'); xlabel('测试集样本','FontSize',12); ylabel('类别标签','FontSize',12); legend('实际测试集分类','预测测试集分类'); title('测试集的实际分类和预测分类图','FontSize',12); grid on snapnow %% 显示程序运行时间 toc % This function initialize the first population of search agents function Positions=initialization(SearchAgents_no,dim,ub,lb) Boundary_no= size(ub,2); % numnber of boundaries % If the boundaries of all variables are equal and user enter a signle % number for both ub and lb if Boundary_no==1 Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb; end % If each variable has a different lb and ub if Boundary_no>1 for i=1:dim ub_i=ub(i); lb_i=lb(i); Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i; end end （广告）欢迎扫描关注微信公众号：Genlovhyy的数据小站(Gnelovy212) 作者：u013337691 发表于2016/9/8 10:26:19  原文链接 阅读：764 评论：2  查看评论

[原]CS（布谷鸟搜索）算法MATLAB源码逐行中文注解

以优化SVM算法的参数c和g为例，对CS算法MATLAB源码进行了逐行中文注解。  完整程序和示例文件地址：http://download.csdn.net/detail/u013337691/9622335  链接：http://pan.baidu.com/s/1sl2BzKL 密码：pkdn tic % 计时 %% 清空环境导入数据 clear clc close all load wndspd % 示例数据为风速（时间序列）数据，共144个样本 % 训练/测试数据准备（用前3天预测后一天）,用前100天做测试数据 train_input(1,:)=wndspd(1:97); train_input(2,:)=wndspd(2:98); train_input(3,:)=wndspd(3:99); train_output=[wndspd(4:100)]'; test_input(1,:)=wndspd(101:end-3); test_input(2,:)=wndspd(102:end-2); test_input(3,:)=wndspd(103:end-1); test_output=[wndspd(104:end)]'; [input_train,rule1]=mapminmax(train_input); [output_train,rule2]=mapminmax(train_output); input_test=mapminmax('apply',test_input,rule1); output_test=mapminmax('apply',test_output,rule2); %% CS-SVR time=20; n=20; % n为巢穴数量 pa=0.25; % 被宿主发现的概率 dim = 2; % 需要寻优的参数个数 Lb=[0.01,0.01]; % 设置参数下界 Ub=[100,100]; % 设置参数上界 % 随机初始化巢穴 nest=zeros(n,dim); for i=1:n % 遍历每个巢穴 nest(i,:)=Lb+(Ub-Lb).*rand(size(Lb)); % 对每个巢穴，随机初始化参数 end fitness=ones(1,n); % 目标函数值初始化 [fmin,bestnest,nest,fitness]=get_best_nest(nest,nest,fitness,input_train,output_train,input_test,output_test); % 找出当前最佳巢穴和参数 %% 迭代开始 for t=1:time new_nest=get_cuckoos(nest,bestnest,Lb,Ub); % 保留当前最优解，寻找新巢穴 [~,~,nest,fitness]=get_best_nest(nest,new_nest,fitness,input_train,output_train,input_test,output_test); % 找出当前最佳巢穴和参数 new_nest=empty_nests(nest,Lb,Ub,pa); % 发现并更新劣质巢穴 % 找出当前最佳巢穴和参数 [fnew,best,nest,fitness]=get_best_nest(nest,new_nest,fitness,input_train,output_train,input_test,output_test); if fnewend end %% 打印参数选择结果 bestobjfun=fmin; bestc=bestnest(1); bestg=bestnest(2); disp('打印参数选择结果'); str=sprintf('Best c = %g，Best g = %g',bestc,bestg); disp(str) %% 利用回归预测分析最佳的参数进行SVM网络训练 cmd_cs_svr=['-s 3 -t 2',' -c ',num2str(bestnest(1)),' -g ',num2str(bestnest(2))]; model_cs_svr=svmtrain(output_train',input_train',cmd_cs_svr); % SVM模型训练 %% SVM网络回归预测 [output_test_pre,acc]=svmpredict(output_test',input_test',model_cs_svr); % SVM模型预测及其精度 test_pre=mapminmax('reverse',output_test_pre',rule2); test_pre = test_pre'; err_pre=wndspd(104:end)-test_pre; figure('Name','测试数据残差图') set(gcf,'unit','centimeters','position',[0.5,5,30,5]) plot(err_pre,'*-'); figure('Name','原始-预测图') plot(test_pre,'*r-');hold on;plot(wndspd(104:end),'bo-'); legend('预测','原始') set(gcf,'unit','centimeters','position',[0.5,13,30,5]) result=[wndspd(104:end),test_pre]; MAE=mymae(wndspd(104:end),test_pre) MSE=mymse(wndspd(104:end),test_pre) MAPE=mymape(wndspd(104:end),test_pre) %% 显示程序运行时间 toc （广告）欢迎扫描关注微信公众号：Genlovhyy的数据小站(Gnelovy212)  作者：u013337691 发表于2016/9/5 18:53:51  原文链接 阅读：347 评论：1  查看评论

[原]ABC（智能蜂群算法）优化SVM_源码逐行中文注解

​最近发现要彻底、快速地弄懂一个算法，最好的办法就是找源码来，静下心，一行一行的学习。所以我把ABC算法的源码找来逐行做了中文注释，并以优化SVM参数为例，进行学习。 废话不多说，直接上MATLAB代码（ABC-SVR）： tic % 计时 %% 清空环境，准备数据 clear clc close all load wndspd % 示例数据为风速（时间序列）数据，共144个样本 % 训练/测试数据准备（用前3天预测后一天）,用前100天的数据做训练 train_input(1,:)=wndspd(1:97); train_input(2,:)=wndspd(2:98); train_input(3,:)=wndspd(3:99); train_output=[wndspd(4:100)]'; test_input(1,:)=wndspd(101:end-3); test_input(2,:)=wndspd(102:end-2); test_input(3,:)=wndspd(103:end-1); test_output=[wndspd(104:end)]'; % 数据归一化处理 [input_train,rule1]=mapminmax(train_input); [output_train,rule2]=mapminmax(train_output); input_test=mapminmax('apply',test_input,rule1); output_test=mapminmax('apply',test_output,rule2); %% %%%%%%%%%%%%%用ABC算法优化SVR中的参数c和g开始%%%%%%%%%%%%%%%%%%%% %% 参数初始化 NP=20; % 蜂群规模 FoodNumber=NP/2; % 蜜源（解）数量 limit=100; % 当有蜜源连续没被更新的次数超过limit时，该蜜源将被重新初始化 maxCycle=10; % 最大迭代次数 % 待优化参数信息 D=2; % 待优化参数个数，次数为c和g两个 ub=ones(1,D)*100; % 参数取值上界，此处将c和g的上界设为100 lb=ones(1,D)*(0.01); % 参数取值下界，此处将c和g的下界设为0.01 runtime=2; % 可用于设置多次运行（让ABC算法运行runtime次）以考察程序的稳健性 BestGlobalMins=ones(1,runtime); % 全局最小值初始化，这里的优化目标为SVR预测结果中的平均平方误差（MSE），初始化为最差值1 BestGlobalParams=zeros(runtime,D); % 用于存放ABC算法优化得到的最优参数 for r=1:runtime % 运行ABC算法runtime次 % 初始化蜜源 Range = repmat((ub-lb),[FoodNumber 1]); Lower = repmat(lb, [FoodNumber 1]); Foods = rand(FoodNumber,D) .* Range + Lower; % 计算每个蜜源（解）得目标函数值，fobj为计算SVR预测的平均平方误差（MSE）的函数，根据自己的实际问题变异目标函数即可 ObjVal=ones(1,FoodNumber); for k = 1:FoodNumber ObjVal(k) = fobj(Foods(k,:),input_train,output_train,input_test,output_test); end Fitness=calculateFitness(ObjVal); % 计算适应度函数值 trial=zeros(1,FoodNumber); % 用于记录第i个蜜源有连续trail(i)次没被更新过 % 标记最优蜜源（解） BestInd=find(ObjVal==min(ObjVal)); BestInd=BestInd(end); GlobalMin=ObjVal(BestInd); % 更新全局最优目标函数值 GlobalParams=Foods(BestInd,:); % 更新全局最优参数为最优蜜源 iter=1; % 迭代开始 while ((iter <= maxCycle)) % 循环条件 %%%%%%%%%%%%%%%%%%%%%引领蜂搜索解的过程%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% for i=1:(FoodNumber) % 遍历每个蜜源（解） Param2Change=fix(rand*D)+1; % 随机选择需要变异的参数 neighbour=fix(rand*(FoodNumber))+1; % 随机选择相邻蜜源（解）以准备变异 % 需要保证选择的相邻蜜源不是当前蜜源（i） while(neighbour==i) neighbour=fix(rand*(FoodNumber))+1; end sol=Foods(i,:); % 提取当前蜜源（解）对应的的参数 % 参数变异得到新的蜜源：v_{ij}=x_{ij}+\phi_{ij}*(x_{kj}-x_{ij}) sol(Param2Change)=Foods(i,Param2Change)+(Foods(i,Param2Change)-Foods(neighbour,Param2Change))*(rand-0.5)*2; % 确保参数取值范围不越界 ind=find(solub); sol(ind)=ub(ind); % 计算变异后蜜源的目标函数值和适应度函数值 ObjValSol=fobj(sol,input_train,output_train,input_test,output_test); FitnessSol=calculateFitness(ObjValSol); % 更新当前蜜源的相关信息 if (FitnessSol>Fitness(i)) Foods(i,:)=sol; Fitness(i)=FitnessSol; ObjVal(i)=ObjValSol; trial(i)=0; % 如果当前蜜源被更新了，则对应的trial归零 else trial(i)=trial(i)+1; % 如果当前蜜源没有被更新，则trial(i)加1 end end %%%%%%%%%%%%%%%%%%%%%%%% 跟随蜂搜索解的过程 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 计算解（蜜源）的概率 prob=(0.9.*Fitness./max(Fitness))+0.1; % 循环初始化 i=1; t=0; while(t<FoodNumber) % 循环条件 if(rand1; % 循环计数器加1 Param2Change=fix(rand*D)+1; % 随机确定需要变异的参数 neighbour=fix(rand*(FoodNumber))+1; % 随机选择相邻蜜源（解） % 需要保证选择的相邻蜜源不是当前蜜源（i） while(neighbour==i) neighbour=fix(rand*(FoodNumber))+1; end sol=Foods(i,:); % 提取当前蜜源i（解）对应的的参数 % 参数变异得到新的蜜源：v_{ij}=x_{ij}+\phi_{ij}*(x_{kj}-x_{ij}) sol(Param2Change)=Foods(i,Param2Change)+(Foods(i,Param2Change)-Foods(neighbour,Param2Change))*(rand-0.5)*2; % 防止参数越界 ind=find(solub); sol(ind)=ub(ind); % 计算变异后蜜源的目标函数值和适应度函数值 ObjValSol=fobj(sol,input_train,output_train,input_test,output_test); FitnessSol=calculateFitness(ObjValSol); % 更新当前蜜源的相关信息 if (FitnessSol>Fitness(i)) Foods(i,:)=sol; Fitness(i)=FitnessSol; ObjVal(i)=ObjValSol; trial(i)=0; % 如果当前蜜源被更新了，则对应的trial归零 else trial(i)=trial(i)+1; % 如果当前蜜源没有被更新，则trial(i)加1 end end i=i+1; % 更新i if (i==(FoodNumber)+1) % 若值超过蜜源数量，则i重新初始化 i=1; end end % 记住最优蜜源 ind=find(ObjVal==min(ObjVal)); ind=ind(end); if (ObjVal(ind)<GlobalMin) GlobalMin=ObjVal(ind); GlobalParams=Foods(ind,:); end %%%%%%%%%%%% 侦查蜂搜索解的过程 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 找出连续最多次都没有被更新的蜜源 ind=find(trial==max(trial)); ind=ind(end); % 如果连续没有更新的次数大于限定次数，则由侦查蜂重新初始化该蜜源 if (trial(ind)>limit) Bas(ind)=0; sol=(ub-lb).*rand(1,D)+lb; ObjValSol=fobj(sol,input_train,output_train,input_test,output_test); FitnessSol=calculateFitness(ObjValSol); Foods(ind,:)=sol; Fitness(ind)=FitnessSol; ObjVal(ind)=ObjValSol; end iter=iter+1; end % 一次ABC算法完结 BestGlobalMins(r)=GlobalMin; % 记录本次ABC算法的最优目标函数值 BestGlobalParams(r,:)=GlobalParams; % 记录本次ABC算法的最优参数 end % end of runs %% %%%%%%%%%%%%%用ABC算法优化SVR中的参数c和g结束%%%%%%%%%%%%%%%%%%%% %% 打印参数选择结果，这里输出的是最后一次ABC算法寻优得到的参数 bestc=GlobalParams(1); bestg=GlobalParams(2); disp('打印选择结果'); str=sprintf('Best c = %g，Best g = %g',bestc,bestg); disp(str) %% 利用回归预测分析最佳的参数进行SVM网络训练 cmd_cs_svr=['-s 3 -t 2',' -c ',num2str(bestc),' -g ',num2str(bestg)]; model_cs_svr=svmtrain(output_train',input_train',cmd_cs_svr); % SVM模型训练 %% SVM网络回归预测 [output_test_pre,acc]=svmpredict(output_test',input_test',model_cs_svr); % SVM模型预测及其精度 test_pre=mapminmax('reverse',output_test_pre',rule2); test_pre = test_pre'; err_pre=wndspd(104:end)-test_pre; figure('Name','测试数据残差图') set(gcf,'unit','centimeters','position',[0.5,5,30,5]) plot(err_pre,'*-');legend('预测残差：实际-预测',0); figure('Name','原始-预测图') plot(test_pre,'*r-');hold on;plot(wndspd(104:end),'bo-'); legend('预测','原始') set(gcf,'unit','centimeters','position',[0.5,13,30,5]) result=[wndspd(104:end),test_pre]; MAE=mymae(wndspd(104:end),test_pre) MSE=mymse(wndspd(104:end),test_pre) MAPE=mymape(wndspd(104:end),test_pre) %% 显示程序运行时间 toc 完整程序和示例数据文件下载地址：http://download.csdn.net/detail/u013337691/9621448 （广告）欢迎扫描关注微信公众号：Genlovhyy的数据小站(Gnelovy212)  作者：u013337691 发表于2016/9/4 17:22:57  原文链接 阅读：334 评论：0  查看评论

[原]用基于信息熵的topsis方法实现学生成绩的综合排名

TOPSIS方法排序的基本思路是首先定义决策问题的正理想解（即最好的）和负理想解（即最坏的），然后把实际可行解（样本）和正理想解与负理想解作比较。通过计算实际可行解与正理想解和负理想解的加权欧氏距离，得出实际可行解与正理想解的接近程度，以此作为排序的依据。若某个可行解（样本）最靠近理想解，同时又最远离负理想解,则此解排序最靠前。  通常，当排序时有多个指标需要考虑时，常用“专家打分法”来确定各个指标的权重，这容易造成评价结果可能由于人的主观因素而形成较大偏差。熵值法能较客观地反映数据本身信息的有序性,它通过评价指标值构成的判断矩阵来确定指标的权重，这样能尽量消除各因素权重的主观性，使评价结果更符合实际。  下面通过MATLAB实现基于信息熵的topsis方法，学习代码的同时也就弄清楚topsis方法的原理了： %% 熵topsis方法的MATLAB实现，以“兰州大学数学与统计学院2015年应用统计硕士研究生复试分数”为例 %% 清空环境，导入数据 clear clc close all % 兰州大学数学与统计学院2015年应用统计硕士研究生复试分数 % 成绩包括：初试总分X1、复试笔试成绩X2、复试专业面试成绩X3、复试外语笔试成绩X4、复试外语口语及听力测试成绩X5，共五个科目 % 原始排名计算方法：总分=（X1/5）*0.5+X2*0.2+（((X4+X5)/2)*0.2+X3*0.8）*0.3 load score data=score(:,2:end); %% 数据归一化处理 [n,m]=size(data); maxdata=repmat(max(data),n,1); mindata=repmat(min(data),n,1); max_min=maxdata-mindata; stddata=(data-mindata)./max_min; %% 利用信息熵计算不同科目的权重 f=(1+stddata)./repmat(sum(1+stddata),n,1); e=-1/log(n)*sum(f.*log(f)); d=1-e; w=d/sum(d); % 权重向量 %% 计算加权决策矩阵，确定正理想解和负理想解 normdata=repmat(w,n,1).*stddata; % 加权决策矩阵 posideal=max(normdata); % 正理想解 negideal=min(normdata); % 负理想解 %% 计算加权后的决策数据与正负理想解的欧式距离 dtopos=sqrt(sum((normdata-repmat(posideal,n,1)).^2,2)); dtoneg=sqrt(sum((normdata-repmat(negideal,n,1)).^2,2)); %% 计算各样本与理想解得接近程度并得到排序结果 d=dtoneg./(dtoneg+dtopos); [dscore,index]=sort(d,'descend'); %% 结果对比 result=[{'新名次'},{'原名次'},{'名次变化'};num2cell(score(:,1)), num2cell(index),num2cell(index-score(:,1))] 程序运行结果如下：  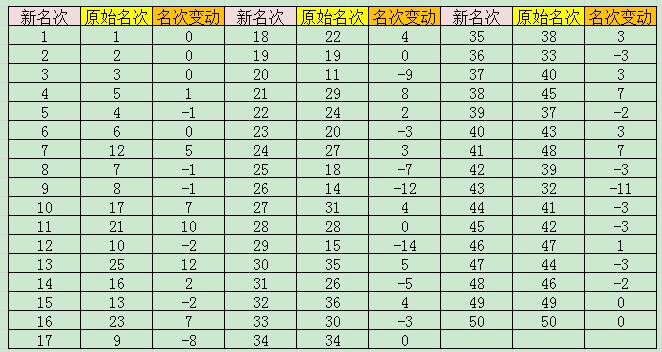作者：u013337691 发表于2016/8/8 14:20:48  原文链接 阅读：247 评论：0  查看评论

[原]Python爬虫实践：从中文歌词库抓取歌词

利用BeautifulSoup库构建一个简单的网络爬虫，从中文歌词库网站抓取凤凰传奇所有曲目的歌词（http://www.cnlyric.com/geshou/1927.html）。 from urllib.request import urlopen from bs4 import BeautifulSoup import re import numpy import csv starturl="http://www.cnlyric.com/geshou/1927.html" # 凤凰传奇歌词地址第一页 # 找出下一页的链接 def findnextlinks(starturl,nextlinks): """ 该函数用于从starturl页面开始，递归找出所有“下一页”的链接地址 要求nextlinks为一个空的列表""" try: html=urlopen(starturl) bsobj=BeautifulSoup(html,"lxml") nextpagelink=bsobj.find("div",{"class":"PageList"}).input.\ previous_sibling.previous_sibling.attrs["href"] nextlink="http://www.cnlyric.com/geshou/"+nextpagelink nextlinks.append(nextlink) findnextlinks(nextlink,nextlinks) except: print("\n所有“下一页”的链接寻找完毕") return nextlinks nextlinks=[] nextlinks=findnextlinks(starturl,nextlinks) # 所有“下一页”的链接列表 # 找出存放歌词的链接列表 def findlrclinks(urllists): """ 该函数用于找出列表urllists中的链接页面上存放歌词的链接 """ Sites=[] for urllist in urllists: html=urlopen(urllist) bsobj=BeautifulSoup(html,"lxml") for link in bsobj.findAll(href=re.compile("^(../LrcXML/)")): site="http://www.cnlyric.com"+link.attrs["href"].lstrip("..") Sites.append(site) return Sites nextlinks.insert(0,starturl) # 将开始页面也加入链接列表中 Sites=findlrclinks(nextlinks) # 找出所有存放歌词的链接 print("\n所有曲目歌词所在的xml文件链接寻找完毕") def getlrc(lrclink): """ 该函数用于找出歌词链接lrclink中的歌词，并以列表形式保存 """ LRC=[] html=urlopen(lrclink) bsobj=BeautifulSoup(html,"lxml") lrcpre=bsobj.findAll("lrc") for lrclabel in lrcpre: lrc=lrclabel.get_text() LRC.append(lrc) return LRC csvfile=open("凤凰传奇歌词集.csv","w+") # 创建csv文件用于保存数据 try: writer=csv.writer(csvfile) rowindex=1 for lrcurl in Sites: LRC=getlrc(lrcurl) LRC.insert(0,str(rowindex).zfill(3)) writer.writerow(LRC) # 将每首哥编号并将歌词写入从中文件中 rowindex+=1 finally: csvfile.close() # 关闭csv文件 运行结果： 参考资料：Ryan Mitchell著，陶俊杰，陈小莉译《Python网络数据采集》 作者：u013337691 发表于2016/7/19 13:39:39  原文链接 阅读：1021 评论：0  查看评论

[原]Python爬虫实践：获取空气质量历史数据

利用BeautifulSoup库构建一个简单的网络爬虫，从天气后报网站抓取兰州空气质量历史数据（http://www.tianqihoubao.com/aqi/lanzhou.html）。 from urllib.request import urlopen from bs4 import BeautifulSoup import re import numpy import csv def getdatawithtablehead(url): """ 该函数用于获取带表头的数据 """ html=urlopen(url) bsobj=BeautifulSoup(html,"lxml") # 获取BeautifulSoup对象 tablelist=bsobj.findAll("tr") # 获取所有的表格 Dataset=[] tablehead=tablelist[0].get_text().strip("\n").split("\n\n") Dataset.append(tablehead) # 获取表头 for datalist in tablelist[1:]: data=datalist.get_text().replace(" ","").replace("\n\r","").\ strip("\n").split("\n") Dataset.append(data) # 获取当月每一天的数据 return Dataset def getdata(url): """ 该函数用于获取不带表头的数据 """ html=urlopen(url) bsobj=BeautifulSoup(html,"lxml") tablelist=bsobj.findAll("tr") dataset=[] for datalist in tablelist[1:]: data=datalist.get_text().replace(" ","").replace("\n\r","").\ strip("\n").split("\n") dataset.append(data) return dataset # 兰州空气质量指数(AQI)-PM2.5查询地址： starturl="http://www.tianqihoubao.com/aqi/lanzhou.html" html=urlopen(starturl) bsobj=BeautifulSoup(html,"lxml") # 获取BeautifulSoup对象 # 找到所有存放月度数据的网页链接，并以列表的形式按月份先后顺序保存这些链接 Sites=[] for link in bsobj.findAll(href=re.compile("^(/aqi/lanzhou-)")): site="http://www.tianqihoubao.com"+link.attrs['href'] Sites.append(site) Sites.reverse() Dataset=getdatawithtablehead(Sites[0]) # 获取表头和第一个月度数据 for url in Sites[1:]: dataset=getdata(url) Dataset=numpy.row_stack((Dataset,dataset)) # 获取所有月度数据 csvfile=open("Dataset.csv","w+") # 创建csv文件用于保存数据 try: writer=csv.writer(csvfile) for i in range(numpy.shape(Dataset)[0]): writer.writerow((Dataset[i,:])) # 将数据逐行写入csv文件 finally: csvfile.close() # 关闭csv文件 运行结果： 参考资料：Ryan Mitchell著，陶俊杰，陈小莉译《Python网络数据采集》 作者：u013337691 发表于2016/7/13 8:38:40  原文链接 阅读：209 评论：0  查看评论

[原]k近邻（kNN）算法的Python实现（基于欧氏距离）

k近邻算法是机器学习中原理最简单的算法之一，其思想为：给定测试样本，计算出距离其最近的k个训练样本，将这k个样本中出现类别最多的标记作为该测试样本的预测标记。  k近邻算法虽然原理简单，但是其泛华错误率却不超过贝叶斯最有分类器错误率的两倍。所以实际应用中，k近邻算法是一个“性价比”很高的分类工具。  基于欧式距离，用Python3.5实现kNN算法： 主程序： from numpy import* import operator def myED(testdata,traindata): """ 计算欧式距离，要求测试样本和训练样本以array([ [],[],...[] ])的形式组织， 每行表示一个样本，一列表示一个属性""" size_train=traindata.shape[0] # 训练样本量大小 size_test=testdata.shape[0] # 测试样本大小 XX=traindata**2 sumXX=XX.sum(axis=1) # 行平方和 YY=testdata**2 sumYY=YY.sum(axis=1) # 行平方和 Xpw2_plus_Ypw2=tile(mat(sumXX).T,[1,size_test])+\ tile(mat(sumYY),[size_train,1]) EDsq=Xpw2_plus_Ypw2-2*(mat(traindata)*mat(testdata).T) # 欧式距离平方 distances=array(EDsq)**0.5 #欧式距离 return distances def mykNN(testdata,traindata,labels,k): """ kNN算法主函数，labels组织成列表形式 """ size_test=testdata.shape[0] D=myED(testdata,traindata) Dsortindex=D.argsort(axis=0) # 距离排序，提取序号 nearest_k=Dsortindex[0:k,:] # 提取最近k个距离的样本序号 label_nearest_k=array(labels)[nearest_k] # 提取最近k个距离样本的标签 label_test=[] if k==1: label_test=label_nearest_k else: for smp in range(size_test): classcount={} labelset=set(label_nearest_k[:,smp]) # k个近邻样本的标签集合 for label in labelset: classcount[label]=list(label_nearest_k[:,smp]).count(label) # 遍历k个近邻样本的标签，并计数，并以字典保存标签和计数结果 sortedclasscount=sorted(classcount.items(),\ key=operator.itemgetter(1),reverse=True) # 按照计数结果排序 label_test.append(sortedclasscount[0][0]) # 提取出现最多的标签 return label_test,D 示例： # 以下示例数据摘自周志华《机器学习》P202表9.1 labels=[1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0] traindata=array([[0.6970,0.4600],[0.7740,0.3760],[0.6340,0.2640],\ [0.6080,0.3180],[0.5560,0.2150],[0.4030,0.2370],[0.4810,0.1490],\ [0.4370,0.2110],[0.6660,0.0910],[0.2430,0.2670],[0.2450,0.0570],\ [0.3430,0.0990],[0.6390,0.1610],[0.6570,0.1980],[0.3600,0.3700],\ [0.5930,0.0420],[0.7190,0.1030]]) testdata=array([[0.3590,0.1880],[0.3390,0.2410],[0.2820,0.2570],\ [0.7480,0.2320],[0.7140,0.3460],[0.4830,0.3120],[0.4780,0.4370],\ [0.5250,0.3690],[0.7510,0.4890],[0.5320,0.4720],[0.4730,0.3760],\ [0.7250,0.4450],[0.4460,0.4590]]) k=5 label_test,distances=mykNN(testdata,traindata,labels,k) print('\n') print(label_test) 示例结果： >>[1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1] 作者：u013337691 发表于2016/7/11 20:15:18  原文链接 阅读：90 评论：0  查看评论

[原]梯度下降法实现softmax回归MATLAB程序

梯度下降法实现softmax回归MATLAB程序 版权声明：本文原创，转载须注明来源。 解决二分类问题时我们通常用Logistic回归，而解决多分类问题时若果用Logistic回归，则需要设计多个分类器，这是相当麻烦的事情。softmax回归可以看做是Logistic回归的普遍推广（Logistic回归可看成softmax回归在类别数为2时的特殊情况），在多分类问题上softmax回归是一个有效的工具。 关于softmax回归算法的理论知识可参考这两篇博文：http://deeplearning.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92 ；  http://blog.csdn.net/acdreamers/article/details/44663305 。 本文自编mysoftmax_gd函数用于实现梯度下降softmax回归，代码如下（链接：http://pan.baidu.com/s/1geF2WMJ 密码：9x3x）： MATLAB程序代码： function [theta,test_pre,rate] = mysoftmax_gd(X_test,X,label,lambda,alpha,MAX_ITR,varargin) % 该函数用于实现梯度下降法softmax回归 % 调用方式：[theta,test_pre,rate] = mysoftmax_gd(X_test,X,label,lambda,alpha,MAX_ITR,varargin) % X_test：测试输入数据 % X：训练输入数据，组织为m*p矩阵，m为案例个数，p为加上常数项之后的属性个数 % label：训练数据标签，组织为m*1向量（数值型） % lambda：权重衰减参数weight decay parameter % alpha：梯度下降学习速率 % MAX_ITR：最大迭代次数 % varargin：可选参数，输入初始迭代的theta系数，若不输入，则默认随机选取 % theta：梯度下降法的theta系数寻优结果 % test_pre：测试数据预测标签 % rata：训练数据回判正确率 % Genlovy Hoo，2016.06.29. [email protected] %% 梯度下降寻优 Nin=length(varargin); if Nin>1 error('输入太多参数') % 若可选输入参数超过1个，则报错 end [m,p] = size(X); numClasses = length(unique(label)); % 求取标签类别数 if Nin==0 theta = 0.005*randn(p,numClasses); % 若没有输入可选参数，则随机初始化系数 else theta=varargin{1}; % 若有输入可选参数，则将其设定为初始theta系数 end cost=zeros(MAX_ITR,1); % 用于追踪代价函数的值 for k=1:MAX_ITR [cost(k),grad] = softmax_cost_grad(X,label,lambda,theta); % 计算代价函数值和梯度 theta=theta-alpha*grad; % 更新系数 end %% 回判预测 [~,~,Probit] = softmax_cost_grad(X,label,lambda,theta); [~,label_pre] = max(Probit,[],2); index = find(label==label_pre); % 找出预测正确的样本的位置 rate = length(index)/m; % 计算预测精度 %% 绘制代价函数图 figure('Name','代价函数值变化图'); plot(0:MAX_ITR-1,cost) xlabel('迭代次数'); ylabel('代价函数值') title('代价函数值变化图');% 绘制代价函数值变化图 %% 测试数据预测 [mt,pt] = size(X_test); Probit_t = zeros(mt,length(unique(label))); for smpt = 1:mt Probit_t(smpt,:) = exp(X_test(smpt,:)*theta)/sum(exp(X_test(smpt,:)*theta)); end [~,test_pre] = max(Probit_t,[],2); function [cost,thetagrad,P] = softmax_cost_grad(X,label,lambda,theta) % 用于计算代价函数值及其梯度 % X：m*p输入矩阵，m为案例个数，p为加上常数项之后的属性个数 % label：m*1标签向量（数值型） % lambda：权重衰减参数weight decay parameter % theta：p*k系数矩阵，k为标签类别数 % cost：总代价函数值 % thetagrad：梯度矩阵 % P：m*k分类概率矩阵，P（i，j）表示第i个样本被判别为第j类的概率 m = size(X,1); % 将每个标签扩展为一个k维横向量（k为标签类别数），若样本i属于第j类，则 % label_extend（i，j）= 1，否则label_extend（i，j）= 0。 label_extend = [full(sparse(label,1:length(label),1))]'; % 计算预测概率矩阵 P = zeros(m,size(label_extend,2)); for smp = 1:m P(smp,:) = exp(X(smp,:)*theta)/sum(exp(X(smp,:)*theta)); end % 计算代价函数值 cost = -1/m*[label_extend(:)]'*log(P(:))+lambda/2*sum(theta(:).^2); % 计算梯度 thetagrad = -1/m*X'*(label_extend-P)+lambda*theta; clear clc close all load fisheriris % MATLAB自带数据集 % 对标签重新编号并准备训练/测试数据集 index_train = [1:40,51:90,101:140]; index_test = [41:50,91:100,141:150]; species_train = species(index_train); X=[ones(length(species_train),1),meas(index_train,:)]; label = zeros(size(species_train)); label(strcmp('setosa',species_train)) = 1; label(strcmp('versicolor',species_train)) = 2; label(strcmp('virginica',species_train)) = 3; species_test = species(index_test); X_test = [ones(length(species_test),1),meas(index_test,:)]; lambda = 0.004; % 权重衰减参数Weight decay parameter alpha = 0.1; % 学习速率 MAX_ITR=500; % 最大迭代次数 [theta,test_pre,rate] = mysoftmax_gd(X_test,X,label,lambda,alpha,MAX_ITR) clear clc close all load MNISTdata % MNIST数据集 % 准备训练/测试数据集 label = labels(1:9000); % 训练集标签 X = [ones(length(label),1),[inputData(:,1:9000)]']; % 训练集输入数据 label_test = labels(9001:end); % 测试集标签 X_test = [ones(length(label_test),1),[inputData(:,9001:end)]']; % 测试输入数据 lambda = 0.004; % 权重衰减参数Weight decay parameter alpha = 0.1; % 学习速率 MAX_ITR=100; % 最大迭代次数 [theta,test_pre,rate] = mysoftmax_gd(X_test,X,label,lambda,alpha,MAX_ITR) index_t = find(label_test==test_pre); % 找出预测正确的样本的位置 rate_test = length(index_t)/length(label_test); % 计算预测精度 水平有限，敬请指正交流。[email protected] 。 参考资料：  【1】：http://deeplearning.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92  【2】：http://blog.csdn.net/acdreamers/article/details/44663305