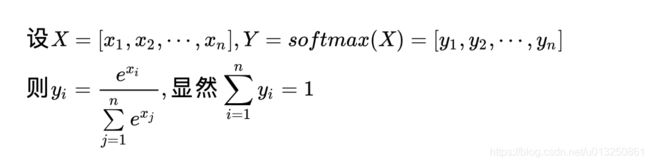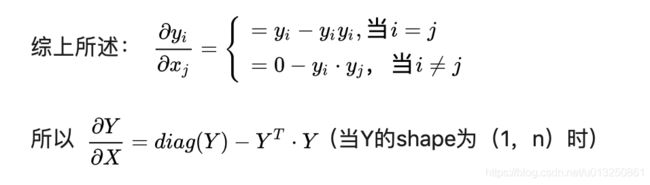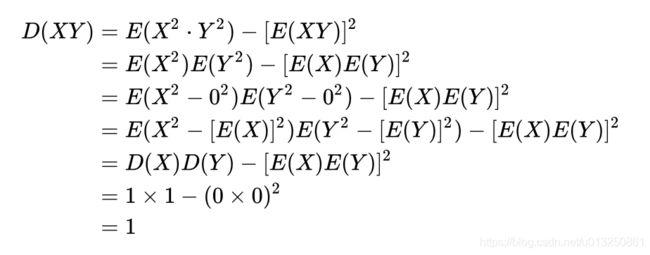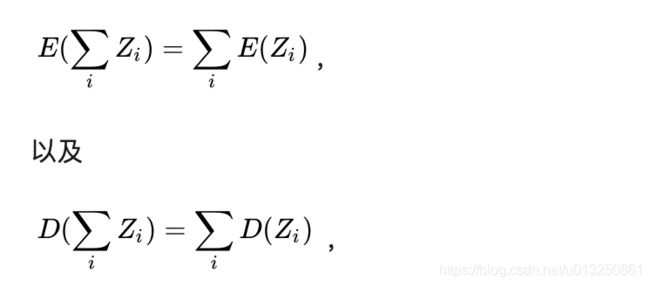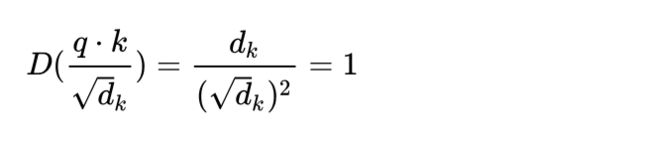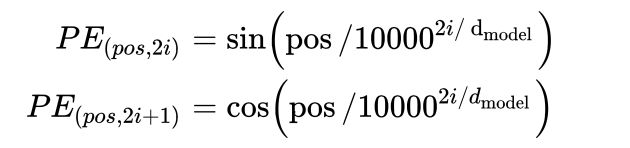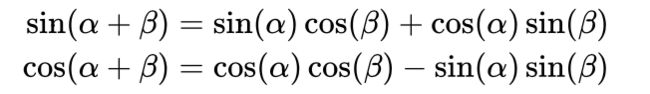NLP-生成模型-2017-Transformer（一）：Encoder-Decoder模型【非序列化；并行计算】【O(n^2·d)，n为序列长度，d为维度】【用正余弦函数进行“绝对位置函数式编码”】

《原始论文：Attention Is All You Need》

一、Transformer 概述

在2017年《Attention Is All You Need》论文里第一次提出Transformer之前，常用的序列模型都是基于卷积神经网络或者循环神经网络，表现最好的模型也是基于encoder- decoder框架的基础加上attention机制。

2018年10月，Google发出一篇论文《BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding》, BERT模型横空出世, 并横扫NLP领域11项任务的最佳成绩!

而在BERT中发挥重要作用的结构就是Transformer, 之后又相继出现XLNet，RoBERT等模型击败了BERT，但是他们的核心没有变，仍然是：Transformer.

相比之前占领市场的LSTM和GRU模型，Transformer有两个显著的优势:

1. Transformer能够利用分布式GPU进行并行训练，提升模型训练效率.
2. 在分析预测更长的文本时, 捕捉间隔较长的语义关联效果更好.

测评比较图:

在著名的SOTA机器翻译榜单https://paperswithcode.com/上, 几乎所有排名靠前的模型都使用Transformer,

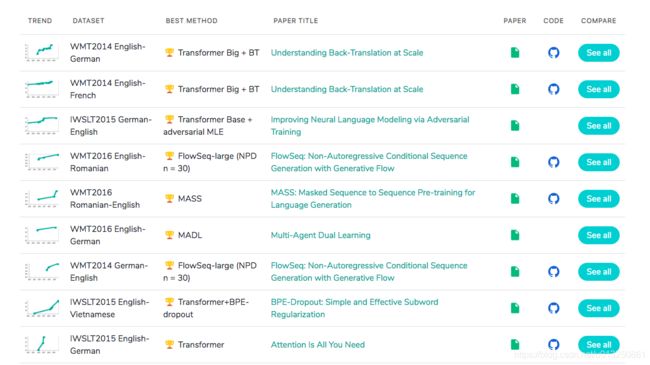
传统Seq2Seq模型中的神经网络一般使用RNN，但是RNN有个缺点：无法并行计算，导致计算特别耗时。

Transformer 是一种基于 Encoder-Decoder 结构、Attention机制、Self-Attention机制的Seq2Seq模型。Transformer 模型中不再使用RNN或CNN做数据转换，而是使用一种Self-Attention Layer结构做数据转换，从而实现并行计算。

Transformer is a kind of Seq2Seq model with “Self-attention” Layer instead of RNN/CNN 。

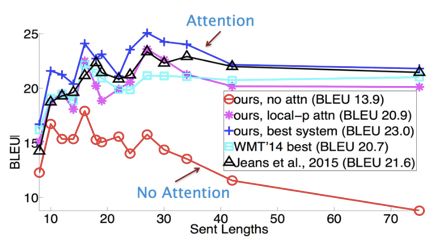
Transformer 在机器翻译任务上的表现超过了 RNN，CNN，只用 encoder-decoder 和 attention 机制就能达到很好的效果，最大的优点是可以高效地并行化。

Transformer模型的作用：基于seq2seq架构的transformer模型可以完成NLP领域研究的典型任务, 如机器翻译, 文本生成等. 同时又可以构建预训练语言模型，用于不同任务的迁移学习.

在接下来的架构分析中, 我们将假设使用Transformer模型架构处理从一种语言文本到另一种语言文本的翻译工作, 因此很多命名方式遵循NLP中的规则. 比如: Embeddding层将称作文本嵌入层, Embedding层产生的张量称为词嵌入张量, 它的最后一维将称作词向量等.

1、Transformer相比于RNN/LSTM有什么优势

对于Transformer比传统序列模型RNN/LSTM具备优势的第一大原因就是强大的并行计算能力.

• 对于RNN来说, 任意时刻t的输入是时刻t的输入x(t)和上一时刻的隐藏层输出h(t-1), 经过运算后得到当前时刻隐藏层的输出h(t), 这个h(t)也即将作为下一时刻t+1的输入的一部分. 这个计算过程是RNN的本质特征, RNN的历史信息是需要通过这个时间步一步一步向后传递的. 而这就意味着RNN序列后面的信息只能等到前面的计算结束后, 将历史信息通过hidden state传递给后面才能开始计算, 形成链式的序列依赖关系, 无法实现并行.
• 对于Transformer结构来说, 在self-attention层, 无论序列的长度是多少, 都可以一次性计算所有单词之间的注意力关系, 这个attention的计算是同步的, 可以实现并行.

对于Transformer比传统序列模型RNN/LSTM具备优势的第二大原因就是强大的特征抽取能力.

• Transformer因为采用了Multi-head Attention结构和计算机制, 拥有比RNN/LSTM更强大的特征抽取能力, 这里并不仅仅由理论分析得来, 而是大量的试验数据和对比结果, 清楚的展示了Transformer的特征抽取能力远远胜于RNN/LSTM.
• 注意: 不是越先进的模型就越无敌, 在很多具体的应用中RNN/LSTM依然大有用武之地, 要具体问题具体分析.

2、为什么说Transformer可以代替seq2seq?

seq2seq的两大缺陷

• 1: seq2seq架构的第一大缺陷是将Encoder端的所有信息压缩成一个固定长度的语义向量中, 用这个固定的向量来代表编码器端的全部信息. 这样既会造成信息的损耗, 也无法让Decoder端在解码的时候去用注意力聚焦哪些是更重要的信息.
• 2: seq2seq架构的第二大缺陷是无法并行, 本质上和RNN/LSTM无法并行的原因一样.

Transformer的改进

• Transformer架构同时解决了seq2seq的两大缺陷, 既可以并行计算, 又应用Multi-head Attention机制来解决Encoder固定编码的问题, 让Decoder在解码的每一步可以通过注意力去关注编码器输出中最重要的那些部分.

3、self-attention公式中的归一化有什么作用? 为什么要添加scaled?

3.1 self-attention中的归一化概述

训练上的意义: 随着词嵌入维度d_k的增大, q * k 点积后的结果也会增大, 在训练时会将softmax函数推入梯度非常小的区域, 可能出现梯度消失的现象, 造成模型收敛困难.

数学上的意义: 假设q和k的统计变量是满足标准正态分布的独立随机变量, 意味着q和k满足均值为0, 方差为1. 那么q和k的点积结果就是均值为0, 方差为d_k, 为了抵消这种方差被放大d_k倍的影响, 在计算中主动将点积缩放1/sqrt(d_k), 这样点积后的结果依然满足均值为0, 方差为1.

3.2 softmax的梯度变化

这里我们分3个步骤来解释softmax的梯度问题:

第一步: softmax函数的输入分布是如何影响输出的.

• 对于一个输入向量x, softmax函数将其做了一个归一化的映射, 首先通过自然底数e将输入元素之间的差距先"拉大", 然后再归一化为一个新的分布. 在这个过程中假设某个输入x中最大的元素下标是k, 如果输入的数量级变大(就是x中的每个分量绝对值都很大), 那么在数学上会造成y_k的值非常接近1.
• 具体用一个例子来演示, 假设输入的向量x = [a, a, 2a], 那么随便给几个不同数量级的值来看看对y3产生的影响

  a = 1时,   y3 = 0.5761168847658291
  a = 10时,  y3 = 0.9999092083843412
  a = 100时, y3 = 1.0
  

• 采用一段实例代码将a在不同取值下, 对应的y3全部画出来, 以曲线的形式展示:

  from math import exp
  from matplotlib import pyplot as plt
  import numpy as np 
  f = lambda x: exp(x * 2) / (exp(x) + exp(x) + exp(x * 2))
  x = np.linspace(0, 100, 100)
  y_3 = [f(x_i) for x_i in x]
  plt.plot(x, y_3)
  plt.show()
  

  得到如下的曲线:
  
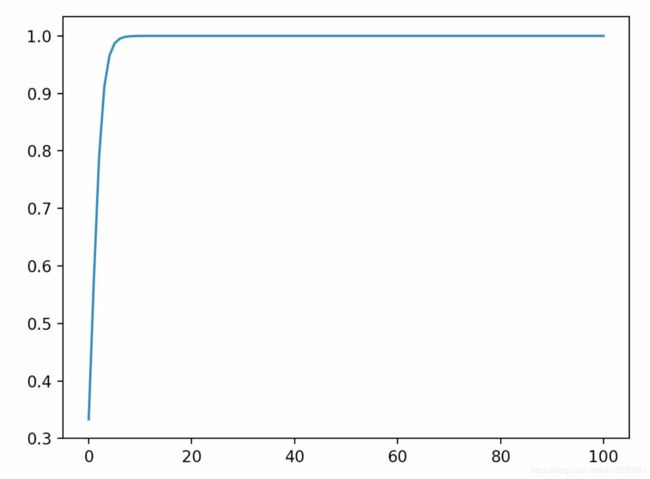
• 从上图可以很清楚的看到输入元素的数量级对softmax最终的分布影响非常之大.
• 结论: 在输入元素的数量级较大时, softmax函数几乎将全部的概率分布都分配给了最大值分量所对应的标签.

第二步: softmax函数在反向传播的过程中是如何梯度求导的.

• 首先定义神经网络的输入和输出:
  
• 反向传播就是输出端的损失函数对输入端求偏导的过程, 这里要分两种情况,
  • 第一种如下所示:
    
  • 第二种如下所示:
    
• 经过对两种情况分别的求导计算, 可以得出最终的结论如下:
  

第三步: softmax函数出现梯度消失现象的原因.

• 根据第二步中softmax函数的求导结果, 可以将最终的结果以矩阵形式展开如下:
  
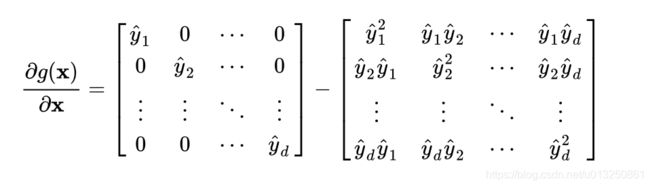
• 根据第一步中的讨论结果, 当输入x的分量值较大时, softmax函数会将大部分概率分配给最大的元素, 假设最大元素是x1, 那么softmax的输出分布将产生一个接近one-hot的结果张量y_ = [1, 0, 0,…, 0], 此时结果矩阵变为:
  
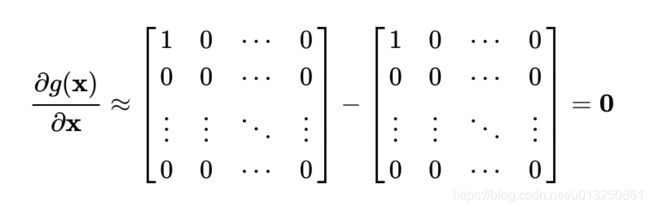
• 结论: 综上可以得出, 所有的梯度都消失为0(接近于0), 参数几乎无法更新, 模型收敛困难.

3.3 维度与点积大小的关系

针对为什么维度会影响点积的大小, 原始论文中有这样的一点解释如下:

To illustrate why the dot products get large, assume that the components of q and k 
are independent random variables with mean 0 and variance 1. Then their doct product,
q*k = (q1k1+q2k2+......+q(d_k)k(d_k)), has mean 0 and variance d_k.

• 我们分两步对其进行一个推导, 首先就是假设向量q和k的各个分量是相互独立的随机变量, X = q_i, Y = k_i, X和Y各自有d_k个分量, 也就是向量的维度等于d_k, 有E(X) = E(Y) = 0, 以及D(X) = D(Y) = 1.

• 可以得到E(XY) = E(X)E(Y) = 0 * 0 = 0

• 同理, 对于D(XY)推导如下:
  

• 根据期望和方差的性质, 对于互相独立的变量满足下式:
  

• 根据上面的公式, 可以很轻松的得出q*k的均值为E(qk) = 0, D(qk) = d_k.

• 所以方差越大, 对应的qk的点积就越大, 这样softmax的输出分布就会更偏向最大值所在的分量.

• 一个技巧就是将点积除以sqrt(d_k), 将方差在数学上重新"拉回1", 如下所示:
  

最终的结论: 通过数学上的技巧将方差控制在1, 也就有效的控制了点积结果的发散, 也就控制了对应的梯度消失的问题!

4 Transformer架构的并行化是如何进行的? 具体体现在哪里?

4.1 Transformer架构中Encoder的并行化

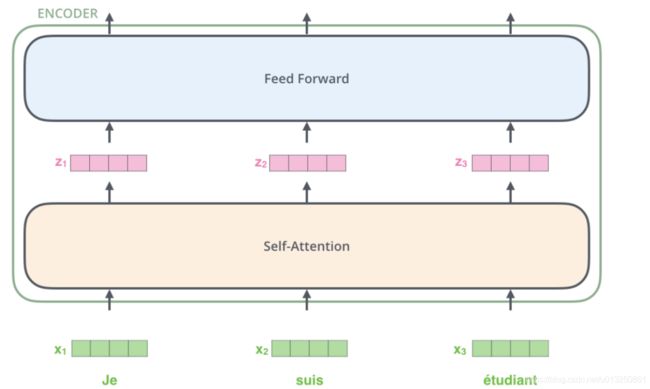
首先Transformer的并行化主要体现在Encoder模块上.

• 1: 上图最底层绿色的部分, 整个序列所有的token可以并行的进行Embedding操作, 这一层的处理是没有依赖关系的.

• 2: 上图第二层土黄色的部分, 也就是Transformer中最重要的self-attention部分, 这里对于任意一个单词比如 $x_1$, 要计算 $x_1$对于其他所有token的注意力分布, 得到 $z_1$. 这个过程是具有依赖性的, 必须等到序列中所有的单词完成Embedding才可以进行. 因此这一步是不能并行处理的. 但是从另一个角度看, 我们真实计算注意力分布的时候, 采用的都是矩阵运算, 也就是可以一次性的计算出所有token的注意力张量, 从这个角度看也算是实现了并行, 只是矩阵运算的"并行"和词嵌入的"并行"概念上不同而已.

• 3: 上图第三层蓝色的部分, 也就是前馈全连接层, 对于不同的向量z之间也是没有依赖关系的, 所以这一层是可以实现并行化处理的. 也就是所有的向量z输入Feed Forward网络的计算可以同步进行, 互不干扰.

4.2 Transformer架构中Decoder的并行化

其次Transformer的并行化也部分的体现在Decoder模块上.

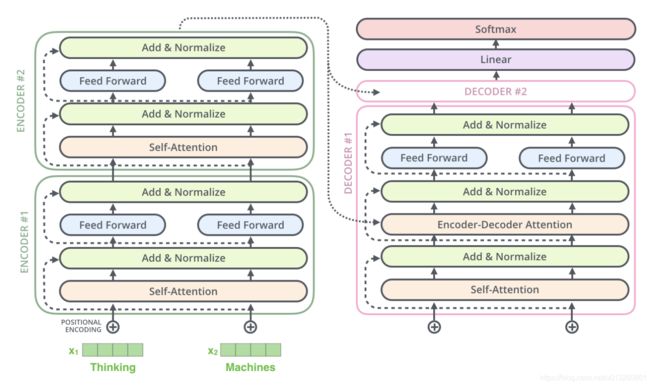
• 1: Decoder模块在训练阶段采用了并行化处理. 其中Self-Attention和Encoder-Decoder Attention两个子层的并行化也是在进行矩阵乘法, 和Encoder的理解是一致的. 在进行Embedding和Feed Forward的处理时, 因为各个token之间没有依赖关系, 所以也是可以完全并行化处理的, 这里和Encoder的理解也是一致的.

• 2: Decoder模块在预测阶段基本上不认为采用了并行化处理. 因为第一个time step的输入只是一个"SOS", 后续每一个time step的输入也只是依次添加之前所有的预测token.

• 3: 注意: 最重要的区别是训练阶段目标文本如果有20个token, 在训练过程中是一次性的输入给Decoder端, 可以做到一些子层的并行化处理. 但是在预测阶段, 如果预测的结果语句总共有20个token, 则需要重复处理20次循环的过程, 每次的输入添加进去一个token, 每次的输入序列比上一次多一个token, 所以不认为是并行处理.

5、Transformer结构特点：

1. 全部用self-attention的自注意力机制。
2. 在self-attention的基础上改进了Multi-Attention和Mask Multi-Attention两种多头注意力机制。
3. 网络由多个层组成，每个层都由多头注意力机制和前馈网络构成。
4. 由于在全局进行注意力机制的计算，忽略了序列中最重要的位置信息，添加了位置编码（Position Encoding），使用正弦函数完成，为每个部分的位置生成位置向量。

Transformer模型在输入时采用的是固定长度序列输入，且Transformer模型的时间复杂度和句子/序列长度的平方成正比（每一层的复杂度：$O(n^2\cdot d)$，$n$ 为句子/序列长度，$d$ 为词向量维度），因此一般序列长度都限制在最大512，因为太大的长度，模型训练的时间消耗太大。

此外Transformer模型又不像RNN这种结构，可以将最后时间输出的隐层向量作为整个序列的表示，然后作为下一序列的初始化输入。所以用Transformer训练语言模型时，不同的序列之间是没有联系的，因此这样的Transformer在长距离依赖的捕获能力是不够的，此外在处理长文本的时候，若是将文本分为多个固定长度的片段，对于连续的文本，这无异于将文本的整体性破坏了，导致了文本的碎片化，这也是Transformer-XL被提出的原因。

6、Transformer复杂度

Transformer的复杂度与输入序列的长度的平方成正比：

$$O(n^2\cdot d)$$

• $n$：表示输入序列长度；
• $d$：表示词向量维度，一般取100/200/300

所以Transformer模型的输入序列的长度不能太大，否则会导致Transformer复杂度指数级增长，训练变慢。

Transformer各类模型中，$n$ 一般最长取 512。

7、Transformer的历史意义

1. 提出self-attention，拉开了非序列化模型的序幕。
2. 为预训练模型的到来打下了坚实的基础

8、Transformer的缺点

尽管 Transformer 最初是为翻译任务而构建的，但最近的趋势表明，它在语言建模上的应用也可以带来显著的效果。但是，为了获得最佳应用，需要对其架构进行一些修改。

为什么？Transformer 有什么问题？

与 RNN 相比，Transformer 的一项重大改进是其捕获长期依赖关系的能力。但是，Transformer 需要存储的中间步骤（梯度）信息比 RNN 要多的多，并且随着序列长度的增加而指数级增加【$O(n^2\cdot d)$，其中 $n$ 表示输入的文本长度】。换句话说，如果你试图一次输入整个文档，内存可能会爆炸（BOOM！）

为了防止出现此问题，早期有些做法是将文档分成固定大小的文本段（Segment），一次训练一段。这虽然解决了内存问题，但是破坏了模型捕获长期依赖关系的能力。例如句子 “The daughter had a nice umbrella | that her mother gave her”，如果 “daughter” 和 “her” 属于不同段。那么在编码 “her 时将无法知晓"daughter” 的信息。

我们知道GPT就是使用Transformer来进行语言模型的建模。因为Transformer要求输入是定长的词序列(不像RNN可以处理长度不确定的输入序列)，太长的截断，不足的padding，这样我们把一个语料库的字符串序列切分成固定长度的segments。它有下面一些问题：

• 由于定长的要求，我们不可能让输入太长。因此虽然Self-Attention机制虽然不太受长度的约束，但是Transformer的语言模型实际能够考虑的上下文就是输入的长度。
• 因为我们在序列语言模型的时候通常很难准确的分句(或者有时候一个句子比最大长度还长)，所以一个Segment很可能不是一个完整的句子(甚至它是从某个句子的中间部分开始的)，这样前面的几个词就很难预测(给人一个没头没脑的句子也很难预测)，因为语言模型是自回归的，一步错步步错。这就是所谓的context fragmentation的问题。
• 预测的性能问题，假设我们要使用Transformer语言模型来计算一个句子的概率(而不是用于下游的任务)，那么我们首先要计算$P(x_1)$，然后计算$P(x_2|x_1)$，……，一直计算到$P(x_T|x_1,\dots ,x_{T-1})$。每个时刻都需要用Transformer计算一次，而不能像RNN那样之前的把历史都编码到一个context向量里。

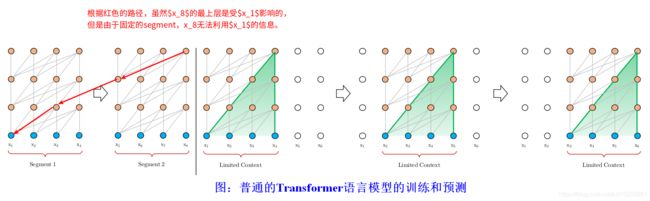
上图做是普通的Transformer语言模型的训练过程。假设Segment的长度为4，如图中我标示的：根据红色的路径，虽然$x_8$的最上层是受$x_1$影响的，但是由于固定的segment，x_8无法利用 $x_1$ 的信息。而预测的时候的上下文也是固定的4，比如预测$x_6$时我们需要根据$[x_2,x_3,x_4,x_5]$来计算，接着把预测的结果作为下一个时刻的输入。接着预测$x_7$的时候需要根据$[x_3,x_4,x_5,x_6]$完全进行重新的计算。之前的计算结果一点也用不上。

如何解决这个问题呢？Transformer-XL。

二、Transformer总体架构

Transformer总体架构可分为四个部分:

• 输入部分
• 输出部分
• 编码器部分
• 解码器部分

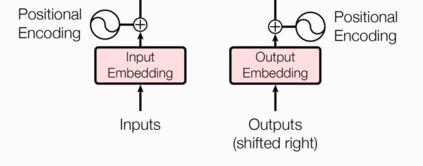
1、输入部分

• 源文本嵌入层及其位置编码器
• 目标文本嵌入层及其位置编码器

1.1 Embedding Layer（文本嵌入层）

Embedding Layer（文本嵌入层）的作用：无论是源文本嵌入还是目标文本嵌入，都是为了将文本中词汇的数字表示转变为向量表示, 由一维转为多维，希望在高维空间捕捉词汇间的关系.

• 文本中的单词在输入到文本嵌入层之前，已经通过word2index操作转换为数值【每个单词用该单词在所在词汇表中的序号表示】，将字符串形式的单词转为序号形式，然后输入到文本嵌入层。
• 再通过文本嵌入层将每个单词的一维的数值型序号转为多维向量。

1.2 Positional Encoding（位置编码器）

位置编码器的作用：因为在Transformer的编码器结构中, 并没有针对词汇位置信息的处理，因此需要在Embedding层后加入位置编码器，将词汇位置不同可能会产生不同语义的信息加入到词嵌入张量中, 以弥补位置信息的缺失.

需要使用位置嵌入的原因也很简单，因为 Transformer 摈弃了 RNN 的结构，因此需要一个东西来标记各个字之间的时序 or 位置关系，而这个东西，就是位置嵌入。

位置编码器中使用sin()函数、cos()函数将所添加的Positional Encoding张量的值域范围控制1到-1，这很好的控制了嵌入数值的大小, 有助于梯度的快速计算.

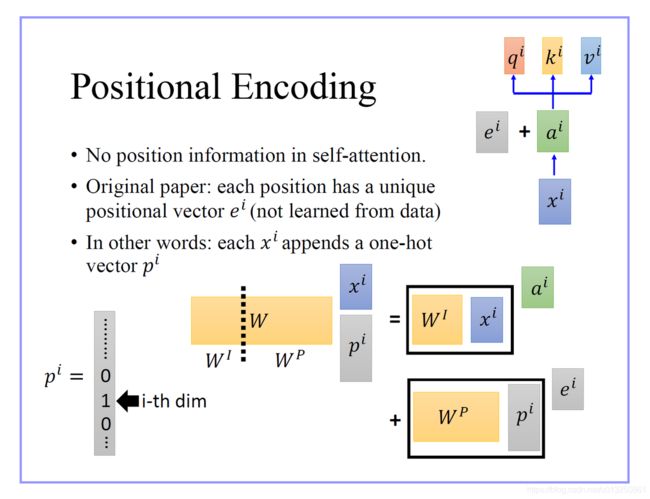
Transformer中直接采用正弦函数和余弦函数来编码位置信息, 如下图所示:

• $d_{model}$ 代表词嵌入维度；
• $i$ 代表当前的维度（从0开始，到$d_{model}/2-1$ 结束）；
• $pos$ 代表当前单词在当前句子中所处的位置索引；
• 维度 $2i$ 以及维度 $2i+1$ 对 位置索引 $pos$ 的缩放因子相等，且都为：$\frac{1}{10000^{2i/d_{model}}}$
• 位置索引 $pos$ 在 维度 $2i$、$2i+1$ 缩放后的值一样，都为 $\frac{pos}{10000^{2i/d_{model}}}$，不同的是：
  • 维度 $2i$ 用sin() 函数进行再次缩放
  • 维度 $2i+1$ 用cos() 函数进行再次缩放；

比如：$d_{model}=512$，句子长度为20，则该句子中第3个单词的位置编码信息（所有512个维度的各个维度的位置编码）为：
$$\begin{array}{rl}& [\\ & sin(\frac{3}{10000^{2\times 0/512}}),cos(\frac{3}{10000^{2\times 0/512}}),\\ & sin(\frac{3}{10000^{2\times 1/512}}),cos(\frac{3}{10000^{2\times 1/512}}),\\ & sin(\frac{3}{10000^{2\times 2/512}}),cos(\frac{3}{10000^{2\times 2/512}}),\\ & ...,\\ & sin(\frac{3}{10000^{2\times 253/512}}),cos(\frac{3}{10000^{2\times 253/512}})\\ & sin(\frac{3}{10000^{2\times 254/512}}),cos(\frac{3}{10000^{2\times 254/512}})\\ ]& \end{array}$$

需要注意: 三角函数应用在此处的一个重要的优点, 因为对于任意的PE(pos+k), 都可以表示为PE(pos)的线性函数, 大大方便计算. 而且周期性函数不受序列长度的限制, 也可以增强模型的泛化能力.

class PositionEncoding(nn.Module):
    def __init__(self, max_seq_len, word_embedding_size):  # max_seq_len: 每个句子的最大长度
        super(PositionEncoding, self).__init__()
        pos_enc = np.array([[pos / np.power(10000, 2.0 * (j // 2) / word_embedding_size) for j in range(word_embedding_size)] for pos in range(max_seq_len)])
        pos_enc[:, 0::2] = np.sin(pos_enc[:, 0::2])
        pos_enc[:, 1::2] = np.cos(pos_enc[:, 1::2])
        pad_row = np.zeros([1, word_embedding_size])
        pos_enc = np.concatenate([pad_row, pos_enc]).astype(np.float32)

        # additional single row for PAD idx
        self.pos_enc = nn.Embedding(max_seq_len + 1, word_embedding_size)
        # fix positional encoding: exclude weight from grad computation
        self.pos_enc.weight = nn.Parameter(torch.from_numpy(pos_enc), requires_grad=False)

    def forward(self, input_len):
        max_len = torch.max(input_len)
        tensor = torch.cuda.LongTensor if input_len.is_cuda else torch.LongTensor
        input_pos = tensor([list(range(1, len + 1)) + [0] * (max_len.item() - len) for len in input_len.cpu().numpy()])
        # 前面123，后面补0

        return self.pos_enc(input_pos)

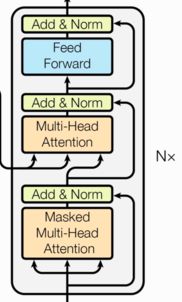
2、编码器

• 由N个编码器层堆叠而成（经典的Transformer结构中的Encoder模块包含6个Encoder Block， 6个一模一样的Encoder Block层层堆叠在一起, 共同组成完整的Encoder）
• 每个编码器层由两个子层连接结构组成
  • 第一个子层连接结构包括一个多头自注意力子层和规范化层以及一个残差连接
  • 第二个子层连接结构包括一个前馈全连接子层和规范化层以及一个残差连接

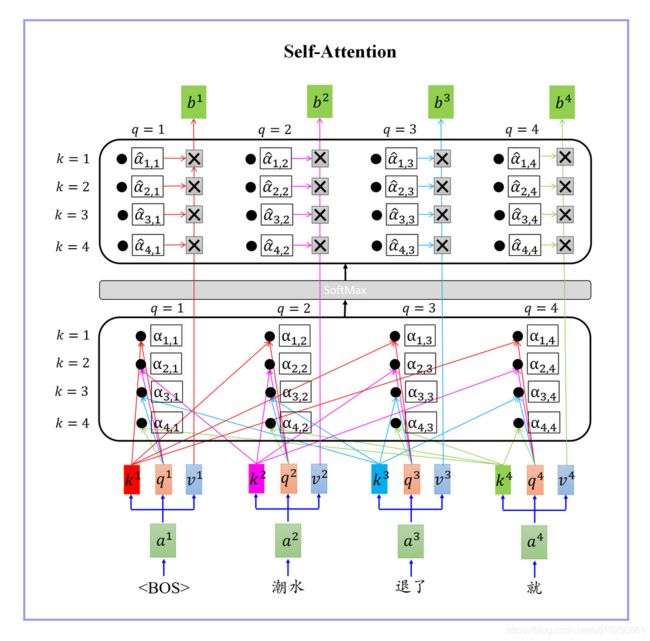
2.1 Self-Attention(自注意力层)内部结构

什么是注意力：我们观察事物时，之所以能够快速判断一种事物(当然允许判断是错误的), 是因为我们大脑能够很快把注意力放在事物最具有辨识度的部分从而作出判断，而并非是从头到尾的观察一遍事物后，才能有判断结果. 正是基于这样的理论，就产生了注意力机制.

注意力计算规则需要三个指定的输入Q(query), K(key), V(value), 然后通过计算公式得到注意力的结果, 这个结果代表query在key和value作用下的注意力表示.

• Q, K, V的比喻解释：Q是一段准备被概括的文本; K是给出的提示; V是大脑中的对提示K的延伸，最终可以用简单的注意力张量来表达较复杂的Q。
• 当输入的Q=K=V时, 称作自注意力计算规则。所给的提示K就是Q本身。

常见的注意力计算规则有三种:

1. 将Q，K进行纵轴拼接, 做一次线性变化, 再使用softmax处理获得结果最后与V做张量乘法.
   $$Attention(Q,K,V)=Softmax(Linear([Q,K]))\cdot V$$

2. 将Q，K进行纵轴拼接, 做一次线性变化后再使用tanh函数激活, 然后再进行内部求和, 最后使用softmax处理获得结果再与V做张量乘法.

$$Attention(Q,K,V)=Softmax(sum(tanh(Linear([Q,K]))))\cdot V$$

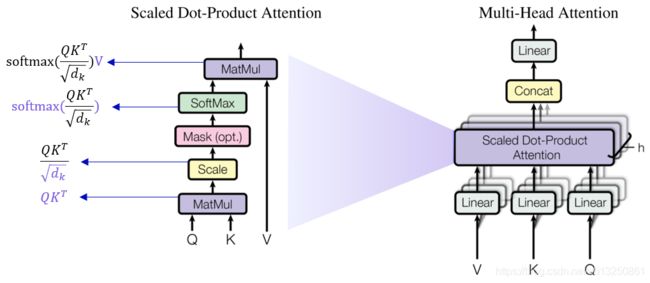
3. 将Q与K的转置做点积运算, 然后除以一个缩放系数, 再使用softmax处理获得结果最后与V做张量乘法.

$$Attention(Q,K,V)=Softmax(\frac{Q\cdot K}{\sqrt{d_k}})\cdot V$$

Q, K, V的比喻解释，假如我们有一个问题: 给出一段文本，使用一些关键词对它进行描述!

• key：为了方便统一正确答案，这道题可能预先已经给大家写出了一些关键词作为提示.其中这些给出的提示就可以看作是key，
• query：而整个的文本信息就相当于是query，
• value：value的含义则更抽象，可以比作是你看到这段文本信息后，脑子里浮现的答案信息，
• 这里我们又假设大家最开始都不是很聪明，第一次看到这段文本后脑子里基本上浮现的信息就只有提示这些信息(即key)，因此key与value基本是相同的，
• 但是随着我们对这个问题的深入理解，通过我们的思考脑子里想起来的东西原来越多，并且能够开始对我们的query(也就是这段文本)提取关键信息进行表示. 这就是注意力作用的过程，
• 通过这个过程，我们最终脑子里的value发生了变化，
• 以上步骤就是根据提示key生成了query的关键词value的方法，也就是另外一种特征表示方法.

一般注意力机制： 刚刚我们说到key和value一般情况下默认是相同，与query是不同的，这种是我们一般注意力机制； 自注意力机制：当query与key和value三者都相同时，这种情况我们称为自注意力机制

• 使用一般注意力机制，是使用不同于给定文本的关键词表示它.
• 使用自注意力机制，需要用给定文本自身来表达自己，也就是说你需要从给定文本中抽取关键词来表述它, 相当于对文本自身的一次特征提取.
  
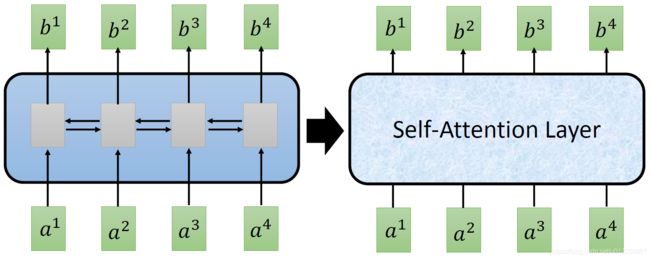
• $b^i$ is obtained based on the whole input sequence。
• $b^1,b^2,b^3,b^4$ can be parallelly computed。
• You can try to replace any thing that has been done by RNN with self-attention。

注意力机制：注意力机制是注意力计算规则能够应用的深度学习网络的载体, 除了注意力计算规则外, 还包括一些必要的全连接层以及相关张量处理, 使其与应用网络融为一体. 使用自注意力计算规则的注意力机制称为自注意力机制.

class ScaledDotProductAttention(nn.Module):
    def __init__(self, d_k, dropout=.1):
        super(ScaledDotProductAttention, self).__init__()
        self.scale_factor = np.sqrt(d_k)
        self.softmax = nn.Softmax(dim=-1)
        self.dropout = nn.Dropout(dropout)

    def forward(self, q, k, v, attn_mask=None):
    	# q、k、v的形状：
        # q: [b_size x n_heads x len_q x d_k]：torch.Size([batchSize * self.num_heads, seqLen, head_dim])
        # k: [b_size x n_heads x len_k x d_k]：torch.Size([batchSize * self.num_heads, seqLen, head_dim])
        # v: [b_size x n_heads x len_v x d_v]：torch.Size([batchSize * self.num_heads, seqLen, head_dim])
        # note: (len_k == len_v)

        # attention_weight: [b_size x n_heads x len_q x len_k]
        scores = torch.matmul(q, k.transpose(-1, -2)) / self.scale_factor
        if attn_mask is not None:
            assert attn_mask.size() == scores.size()
            # 将等于1的地方设置为负无穷 attn_mask = seq_k.data.eq(0).unsqueeze(1)，等于0为True
            scores.masked_fill_(attn_mask, -1e9)
        attention_weight = self.dropout(self.softmax(scores))

        # outputs: [b_size x n_heads x len_q x d_v]
        context_vector = torch.matmul(attention_weight, v)

        return context_vector, attention_weight

Step-01

$$\begin{array}{r}\left[\begin{array}{cccc}{k}^1& k^2& k^3& k^4\end{array}\right]=w^k\cdot \left[\begin{array}{cccc}{a}^1& a^2& a^3& a^4\end{array}\right]\\ \\ \left[\begin{array}{cccc}{q}^1& q^2& q^3& q^4\end{array}\right]=w^q\cdot \left[\begin{array}{cccc}{a}^1& a^2& a^3& a^4\end{array}\right]\\ \\ \left[\begin{array}{cccc}{v}^1& v^2& v^3& v^4\end{array}\right]=w^v\cdot \left[\begin{array}{cccc}{a}^1& a^2& a^3& a^4\end{array}\right]\end{array}$$

Step-02

$$\begin{array}{r}\left[\begin{array}{cccc}{\alpha }_{11}& {\alpha }_{12}& {\alpha }_{13}& {\alpha }_{14}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}& {\alpha }_{24}\\ {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}& {\alpha }_{34}\\ {\alpha }_{41}& {\alpha }_{42}& {\alpha }_{43}& {\alpha }_{44}\end{array}\right]=\frac{\{\left[\begin{array}{c}{k}^1\\ k^2\\ k^3\\ k^4\end{array}\right]\cdot \left[\begin{array}{cccc}{q}^1& q^2& q^3& q^4\end{array}\right]\}}{\sqrt{d}}\end{array}$$
其中：$d$ is the dim of $q$ and $k$，一般就是词向量维度

Step-03：Softmax

$${\hat{\alpha }}_{ij}=\frac{e^{{\alpha }_{ij}}}{{\sum }_{k=1}^4{e}^{{\alpha }_{kj}}}$$

Step-04

$$\begin{array}{r}\left[\begin{array}{cccc}{b}^1& b^2& b^3& b^4\end{array}\right]=\left[\begin{array}{cccc}{v}^1& v^2& v^3& v^4\end{array}\right]\cdot \left[\begin{array}{cccc}{\hat{\alpha }}_{11}& {\hat{\alpha }}_{12}& {\hat{\alpha }}_{13}& {\hat{\alpha }}_{14}\\ {\hat{\alpha }}_{21}& {\hat{\alpha }}_{22}& {\hat{\alpha }}_{23}& {\hat{\alpha }}_{24}\\ {\hat{\alpha }}_{31}& {\hat{\alpha }}_{32}& {\hat{\alpha }}_{33}& {\hat{\alpha }}_{34}\\ {\hat{\alpha }}_{41}& {\hat{\alpha }}_{42}& {\hat{\alpha }}_{43}& {\hat{\alpha }}_{44}\end{array}\right]\end{array}$$

self-attention是一种通过自身和自身进行关联的attention机制, 从而得到更好的representation来表达自身.

self-attention是attention机制的一种特殊情况：在self-attention中, Q=K=V, 序列中的每个单词(token)都和该序列中的其他所有单词(token)进行attention规则的计算。

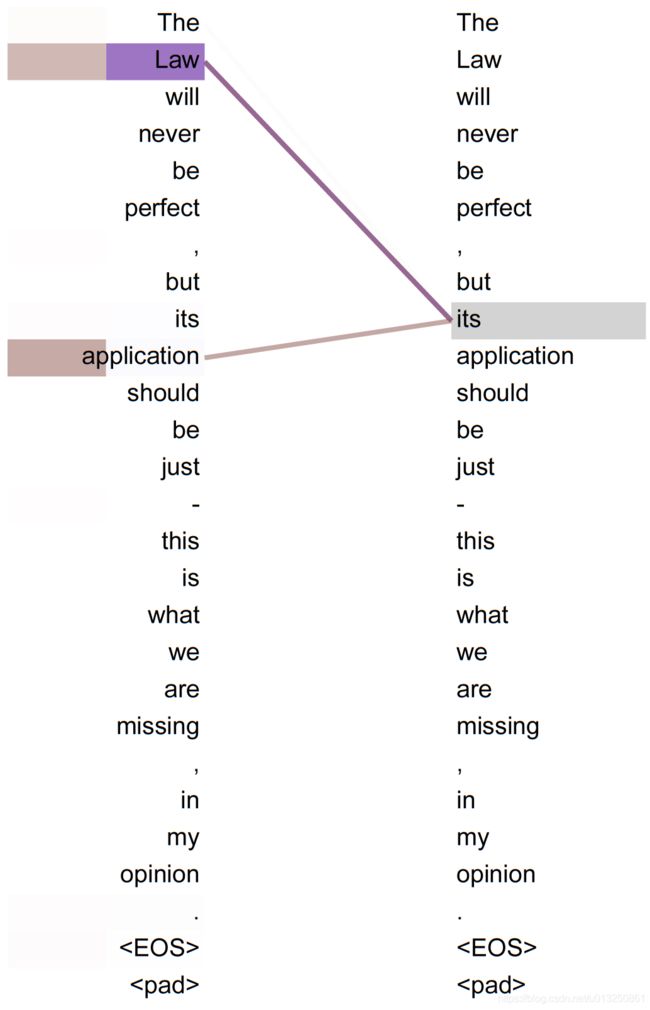
attention机制计算的特点在于, 可以直接跨越一句话中不同距离的token, 可以远距离的学习到序列的知识依赖和语序结构.

• 从上图中可以看到, self-attention可以远距离的捕捉到语义层面的特征(its的指代对象是Law).
• 应用传统的RNN, LSTM, 在获取长距离语义特征和结构特征的时候, 需要按照序列顺序依次计算, 距离越远的联系信息的损耗越大, 有效提取和捕获的可能性越小.
• 但是应用self-attention时, 计算过程中会直接将句子中任意两个token的联系通过一个计算步骤直接联系起来,

关于self-attention为什么要使用(Q, K, V)三元组而不是其他形式:

• 首先一条就是从分析的角度看, 查询Query是一条独立的序列信息, 通过关键词Key的提示作用, 得到最终语义的真实值Value表达, 数学意义更充分, 完备.
• 这里不使用(K, V)或者(V)没有什么必须的理由, 也没有相关的论文来严格阐述比较试验的结果差异, 所以可以作为开放性问题未来去探索, 只要明确在经典self-attention实现中用的是三元组就好.

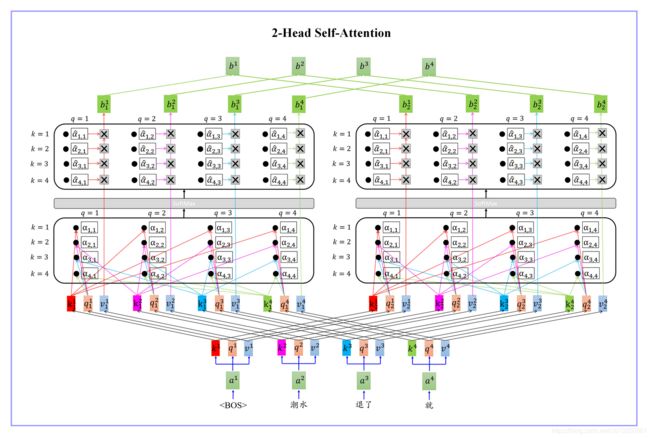
2.2 Multi-Head Self-Attention(多头注意力子层)内部结构

采用Multi-head Attention的原因

• 1: 原始论文中提到进行Multi-head Attention的原因是将模型分为多个头, 可以形成多个子空间, 让模型去关注不同方面的信息, 最后再将各个方面的信息综合起来得到更好的效果.
• 2: 多个头进行attention计算最后再综合起来, 类似于CNN中采用多个卷积核的作用, 不同的卷积核提取不同的特征, 关注不同的部分, 最后再进行融合.
• 3: 直观上讲, 多头注意力有助于神经网络捕捉到更丰富的特征信息.

Multi-head Attention的计算方式：

• 1: Multi-head Attention和单一head的Attention唯一的区别就在于, 其对特征张量的最后一个维度进行了分割, 一般是对词嵌入的embedding_dim=512进行切割成head=8, 这样每一个head的嵌入维度就是512/8=64, 后续的Attention计算公式完全一致, 只不过是在64这个维度上进行一系列的矩阵运算而已.
• 2: 在head=8个头上分别进行注意力规则的运算后, 简单采用拼接concat的方式对结果张量进行融合就得到了Multi-head Attention的计算结果.

多头注意力机制的作用：这种结构设计能让每个注意力机制去优化每个词汇的不同特征部分，从而均衡同一种注意力机制可能产生的偏差，让词义拥有来自更多元的表达。

实验表明多头注意力机制确实可以提升模型效果.

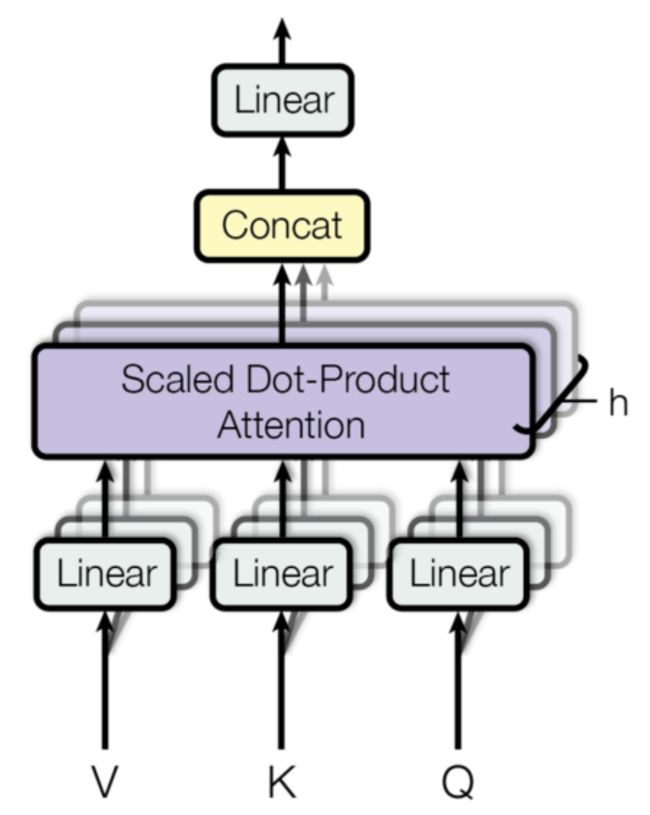
上述的多头self-attention, 对应的数学公式形式如下:

从多头注意力的结构图中，貌似这个所谓的多个头就是指多组线性变换层，其实并不是，只有使用了一组线性变化层

• 三个变换张量(实例化的线性层)对Q，K，V分别进行线性变换，这些变换不会改变原有张量的尺寸，因此每个变换矩阵都是方阵，
• 得到线性变换层输出结果后，多头的作用才开始显现，每个头开始从词义层面分割 “输出的张量”，也就是每个头都想通过分割 “线性变换层输出的张量”获得一组Q，K，V，然后进行注意力机制的计算，但是每个头只获得句子中每个词的词向量的一部分。也就是每个头只分割最后一维的词嵌入向量，得到其中的一部分。
• 比如：词向量总维度为6,被3个head平分,每个head获得词向量中2个维度的数据
• 这就是所谓的多头，将每个头平分获得的词向量中送到注意力机制中, 就形成多头注意力机制。最后再将各个头输出的query的注意力表示进行拼接得到最终的query的注意力表示。

$$\begin{array}{r}{k}_1^i=w_1^k\cdot k^i{k}_2^i=w_2^k\cdot k^i\\ q_1^i=w_1^q\cdot q^i{q}_2^i=w_2^q\cdot q^i\\ v_1^i=w_1^v\cdot v^i{v}_2^i=w_2^v\cdot v^i\end{array}$$

多头注意力机制中需要使用多个相同的线性层, 可以使用克隆函数clones来生成一个克隆线性层列表。

2.3 前馈全连接层

在Transformer中 “前馈全连接层” 就是具有两层线性层的全连接网络，中间有一个Relu激活函数, 对应的数学公式形式如下:

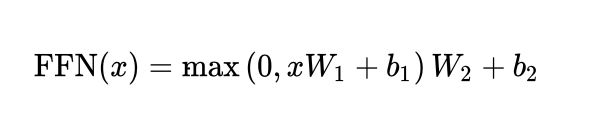
• $x$ ：上一层的输出（一般是Self-Attention层的输出）
• $W_1$、 $W_2$、 $b_1$、 $b_2$ 都是要学习的参数

注意: 原版论文中的前馈全连接层, 输入和输出的维度均为 $d_{model}$ = 512, 层内的连接维度 $d_{ff}$ = 2048, 均采用4倍的大小关系.

前馈全连接层的作用：单纯的多头注意力机制可能对复杂过程的拟合程度不够, 通过增加两层网络来增强模型的能力.

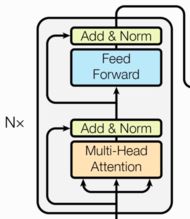
2.4 残差链接&规范化层【Add & Norm】

Add & Norm模块接在每一个Encoder Block和Decoder Block中的每一个子层的后面. 具体来说Add表示残差连接, Norm表示LayerNorm.

• 对于每一个Encoder Block, 里面的两个子层后面都有Add & Norm.
• 对于每一个Decoder Block, 里面的三个子层后面都有Add & Norm.
• 具体的数学表达形式为: LayerNorm(x + Sublayer(x)), 其中Sublayer(x)为子层的输出.

Add残差连接的作用: 和其他神经网络模型中的残差连接作用一致, 都是为了将信息传递的更深, 增强模型的拟合能力. 试验表明残差连接的确增强了模型的表现.

Norm规范化层的作用：规范化层是所有深层网络模型都需要的标准网络层，因为随着网络层数的增加，通过多层的计算后参数可能开始出现过大或过小的情况，这样可能会导致学习过程出现异常，模型可能收敛非常的慢. 因此都会在一定层数后接规范化层进行数值的规范化，使其特征数值在合理范围内.

元素的规范化值=(元素的原始值-元素所在维度均值)/元素所在维度方差
$$\hat{x}=\frac{x-\mu }{\sigma }=\frac{\text{元素的原始值}-\text{元素所在维度均值}}{\text{元素所在维度方差}}$$

class LayerNormalization(nn.Module):
    def __init__(self, d_hid, eps=1e-6):
        super(LayerNormalization, self).__init__()
        self.gamma = nn.Parameter(torch.ones(d_hid))
        self.beta = nn.Parameter(torch.zeros(d_hid))
        self.eps = eps

    def forward(self, z):
        mean = z.mean(dim=-1, keepdim=True, )
        std = z.std(dim=-1, keepdim=True, )
        ln_out = (z - mean) / (std + self.eps)
        ln_out = self.gamma * ln_out + self.beta

        return ln_out

2.5 子层连接结构

如下图所示，输入到每个子层以及规范化层的过程中，还使用了残差链接（跳跃连接），因此我们把这一部分结构整体叫做子层连接（代表子层及其链接结构），在每个编码器层中，都有两个子层，这两个子层加上周围的链接结构就形成了两个子层连接结构.

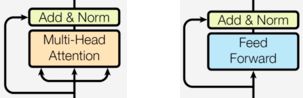
计算注意力权重之前，对Q/K/V的形状要进行转置操作，对第二维和第三维进行转置操作，为了让代表句子长度维度和词向量维度能够相邻，这样注意力机制才能找到词义与句子位置的关系。

import torch
import torch.nn as nn
import torch.nn.init as init

from transformer.modules import Linear
from transformer.modules import ScaledDotProductAttention
from transformer.modules import LayerNormalization

'''
编码器由N个编码器层堆叠而成（经典的Transformer结构中的Encoder模块包含6个Encoder Block， 6个一模一样的Encoder Block层层堆叠在一起, 共同组成完整的Encoder）

每个编码器层（Layer）由两个子层(SubLayer)连接结构组成:
    第一个子层连接结构(SubLayer)包括一个多头自注意力子层和规范化层以及一个残差连接
    第二个子层连接结构(SubLayer)包括一个前馈全连接子层和规范化层以及一个残差连接
'''

class MultiHeadAttention(nn.Module):
    def __init__(self, d_k, d_v, d_model, n_heads, dropout):
        super(MultiHeadAttention, self).__init__()
        self.d_k = d_k
        self.d_v = d_v
        self.d_model = d_model
        self.n_heads = n_heads

        self.w_q = Linear(d_model, d_k * n_heads)
        self.w_k = Linear(d_model, d_k * n_heads)
        self.w_v = Linear(d_model, d_v * n_heads)

        self.attention = ScaledDotProductAttention(d_k, dropout)

    def forward(self, q, k, v, attention_mask):
        b_size = q.size(0)
        # 进入多头处理环节
        # 做完线性变换后，开始为每个头分割输入，这里使用view方法对线性变换的结果进行维度重塑，多加了一个维度 n_heads，代表头数。这样就意味着每个头可以获得一部分词特征组成的句子。
        # 然后对第二维和第三维进行转置操作，为了让代表句子长度维度和词向量维度能够相邻，这样注意力机制才能找到词义与句子位置的关系，
        q_s = self.w_q(q).view(b_size, -1, self.n_heads, self.d_k).transpose(1, 2)  # q: [b_size x len_q x d_model] ----> q_s: [b_size x len_q x n_heads x d_k] ----> q_s: [b_size x n_heads x len_q x d_k]
        k_s = self.w_k(k).view(b_size, -1, self.n_heads, self.d_k).transpose(1, 2)  # k: [b_size x len_k x d_model] ----> k_s: [b_size x len_k x n_heads x d_k] ----> k_s: [b_size x n_heads x len_k x d_k]
        v_s = self.w_v(v).view(b_size, -1, self.n_heads, self.d_v).transpose(1, 2)  # v: [b_size x len_k x d_model] ----> v_s: [b_size x len_k x n_heads x d_v] ----> v_s: [b_size x n_heads x len_k x d_v]

        # 扩展 attention_mask 的维度，使之与 q_s、k_s、v_s 维度一致
        if attention_mask.dim() == 3:  # attention_mask: [b_size x len_q x len_k]
            attention_mask = attention_mask.unsqueeze(1).repeat(1, self.n_heads, 1, 1)

        # 得到每个头的输入后，接下来就是将他们传入到attention中
        context_vector, attention_weight = self.attention(q_s, k_s, v_s, attention_mask=attention_mask)  # context_vector: [b_size x n_heads x len_q x d_v], attention_weight: [b_size x n_heads x len_q x len_k]

        # 合并多头分别计算attention的结果
        context_vector = context_vector.transpose(1, 2)  # 通过多头注意力计算后，得到每个头计算结果组成的(len_q x d_v)维张量，我们需要将其转换为输入的形状以方便后续的计算【进行第一步处理环节的逆操作，对第二和第三维进行转置】[b_size x n_heads x len_q x d_v]---->[b_size x len_q x n_heads x d_v]
        context_vector = context_vector.contiguous().view(b_size, -1, self.n_heads * self.d_v)  # # 使用view重塑形状，变成和输入形状相同，将最后一维大小恢复为embedding_dim【contiguous方法的作用就是能够让转置后的张量应用view方法，否则将无法直接使用】  context_vector: [b_size x len_q x n_heads * d_v]

        return context_vector, attention_weight


class MultiHeadAttnAddNormSubLayer(nn.Module):
    '''
    残差链接 & 规范化层 & 多头注意力层
    '''

    def __init__(self, d_k, d_v, d_model, n_heads, dropout):
        super(MultiHeadAttnAddNormSubLayer, self).__init__()
        self.n_heads = n_heads
        self.multihead_attention = MultiHeadAttention(d_k, d_v, d_model, n_heads, dropout)
        self.proj = Linear(n_heads * d_v, d_model)
        self.dropout = nn.Dropout(dropout)
        self.layer_norm = LayerNormalization(d_model)

    def forward(self, q, k, v, attention_mask):  # q: [b_size x len_q x d_model]; k: [b_size x len_k x d_model]; v: [b_size x len_v x d_model] note (len_k == len_v)
        residual = q
        q = self.layer_norm(q)
        context_vector, attention_weight = self.multihead_attention(q, k, v, attention_mask=attention_mask)  # context_vector: a tensor of shape [b_size x len_q x n_heads * d_v]
        output = self.dropout(self.proj(context_vector))  # project back to the residual size, outputs: [b_size x len_q x d_model]
        output = self.layer_norm(residual + output)

        return output, attention_weight

class FeedForwardAddNormSubLayer(nn.Module):
    '''
    残差链接 & 规范化层 & 前馈层
    '''

    def __init__(self, d_model, d_ff, dropout=0.1):
        super(FeedForwardAddNormSubLayer, self).__init__()
        self.relu = nn.ReLU()
        self.conv1 = nn.Conv1d(in_channels=d_model, out_channels=d_ff, kernel_size=1)
        self.conv2 = nn.Conv1d(in_channels=d_ff, out_channels=d_model, kernel_size=1)
        self.dropout = nn.Dropout(dropout)
        self.layer_norm = LayerNormalization(d_model)

    def forward(self, inputs):
        # inputs: [b_size x len_q x d_model]
        residual = inputs
        output = self.dropout(self.conv2(self.relu(self.conv1(inputs.transpose(1, 2)))).transpose(1, 2))

        return self.layer_norm(residual + output)

2.6 编码器层

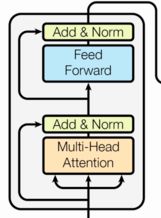
编码器层的作用：作为编码器的组成单元, 每个编码器层完成一次对输入的特征提取过程, 即编码过程。

import torch.nn as nn
from transformer.sublayers import MultiHeadAttnAddNormSubLayer
from transformer.sublayers import MultiBranchAttnAddNormSubLayer
from transformer.sublayers import FeedForwardAddNormSubLayer

class EncoderLayer(nn.Module):
    def __init__(self, d_k, d_v, hidden_size, d_ff, n_heads, dropout=0.1):
        super(EncoderLayer, self).__init__()
        self.encoder_self_attention = MultiHeadAttnAddNormSubLayer(d_k, d_v, hidden_size, n_heads, dropout)
        self.feed_forward = FeedForwardAddNormSubLayer(hidden_size, d_ff, dropout)

    def forward(self, encoder_inputs, encoder_self_attention_mask):
        encoder_outputs, encoder_self_attention_weight = self.encoder_self_attention(encoder_inputs, encoder_inputs, encoder_inputs, attention_mask=encoder_self_attention_mask)
        encoder_outputs = self.feed_forward(encoder_outputs)

        # (batch_size , sen_len, hidden_size)  (batch_size, len_q, len_k)
        return encoder_outputs, encoder_self_attention_weight

2.7 编码器

class PositionEncoding(nn.Module):
    def __init__(self, max_seq_len, word_embedding_size):  # max_seq_len: 每个句子的最大长度
        super(PositionEncoding, self).__init__()
        pos_enc = np.array([[pos / np.power(10000, 2.0 * (j // 2) / word_embedding_size) for j in range(word_embedding_size)] for pos in range(max_seq_len)])
        pos_enc[:, 0::2] = np.sin(pos_enc[:, 0::2])
        pos_enc[:, 1::2] = np.cos(pos_enc[:, 1::2])
        pad_row = np.zeros([1, word_embedding_size])
        pos_enc = np.concatenate([pad_row, pos_enc]).astype(np.float32)

        # additional single row for PAD idx
        self.pos_enc = nn.Embedding(max_seq_len + 1, word_embedding_size)
        # fix positional encoding: exclude weight from grad computation
        self.pos_enc.weight = nn.Parameter(torch.from_numpy(pos_enc), requires_grad=False)

    def forward(self, input_len):
        max_len = torch.max(input_len)
        tensor = torch.cuda.LongTensor if input_len.is_cuda else torch.LongTensor
        input_pos = tensor([list(range(1, len + 1)) + [0] * (max_len.item() - len) for len in input_len.cpu().numpy()])
        # 前面123，后面补0

        return self.pos_enc(input_pos)

import torch
import torch.nn as nn
import numpy as np
from transformer.modules import PositionEncoding
from transformer.layers import EncoderLayer

def get_attention_paddiing_mask(seq_q, seq_k):
    assert seq_q.dim() == 2 and seq_k.dim() == 2
    b_size, len_q = seq_q.size()
    b_size, len_k = seq_k.size()
    pad_attn_mask = seq_k.data.eq(0).unsqueeze(1)  # b_size x 1 x len_k
    return pad_attn_mask.expand(b_size, len_q, len_k)  # b_size x len_q x len_k

class Encoder(nn.Module):
    def __init__(self, n_layers, d_k, d_v, d_model, d_ff, n_heads, max_seq_len, src_vocab_size, dropout=0.1, weighted=False):
        # n_layers: Layer层数量
        # d_k,d_v：用于计算Attention的K、V的维度;
        # d_model: 模型中间隐藏层的维度;
        # d_ff: FeedForward网络的中间隐藏层的维度;
        # n_head: 多头注意力机制的头数;
        # max_seq_len: 输入文本最大长度;
        # src_vocab_size: 源语言词表大小;
        super(Encoder, self).__init__()
        self.d_model = d_model
        self.src_emb = nn.Embedding(num_embeddings=src_vocab_size, embedding_dim=d_model, padding_idx=0)
        self.pos_emb = PositionEncoding(max_seq_len * 10, d_model)
        self.dropout_emb = nn.Dropout(dropout)
        self.encoder_layer = EncoderLayer if not weighted else WeightedEncoderLayer
        self.encoder_layers = nn.ModuleList([self.encoder_layer(d_k, d_v, d_model, d_ff, n_heads, dropout) for _ in range(n_layers)])

    def forward(self, encoder_input_ids, encoder_inputs_len, return_attention_weight=False):  # encoder_input_ids: (batch_size, sen_len)
        encoder_inputs = self.dropout_emb(self.src_emb(encoder_input_ids) + self.pos_emb(encoder_inputs_len))  # 序列化后的输入文本经过文本嵌入层、位置编码层、Dropout层
        encoder_self_attention_mask = get_attention_paddiing_mask(encoder_input_ids, encoder_input_ids)

        encoder_self_attention_weights = []  # 用于存放每一层Layer得到的encoder_self_attention_weight

        # 将encoder_inputs依次经过多层 Encoder Layer
        for layer_idx, encoder_layer in enumerate(self.encoder_layers):
            if layer_idx == 0:  # 第一层decoder_layer是以位置编码层的输出作为输入，之后所有的decoder_layer都是以上一层的decoder_layer的输出作为输入
                encoder_inputs = encoder_inputs
            else:
                encoder_inputs = encoder_outputs
            encoder_outputs, encoder_self_attention_weight = encoder_layer(encoder_inputs=encoder_inputs, encoder_self_attention_mask=encoder_self_attention_mask)
            if return_attention_weight:
                encoder_self_attention_weights.append(encoder_self_attention_weight)

        # encoder_outputs: 输入文本中的所有序列化的词汇id转为词向量(batch_size, src_sen_len, d_model)
        return encoder_outputs, encoder_self_attention_weights

3、解码器

解码器的作用：根据编码器的结果以及上一次预测的结果, 对下一次可能出现的’值’进行特征表示。

• 由N个解码器层堆叠而成
• 每个解码器层由三个子层连接结构组成
  • 第一个子层连接结构包括
    • 一个掩码多头自注意力子层（Masked Decoder-Decoder Self-Attention Layer）
    • 规范化层
    • 一个残差连接
  • 第二个子层连接结构包括
    • 一个多头注意力子层（Encoder-Decoder Attention Layer）
    • 规范化层
    • 一个残差连接
  • 第三个子层连接结构包括
    • 一个前馈全连接子层（Feed-Forward Layer）
    • 规范化层
    • 一个残差连接

import torch
import torch.nn as nn
import numpy as np
from transformer.modules import PositionEncoding
from transformer.layers import DecoderLayer

def get_attention_paddiing_mask(seq_q, seq_k):
    assert seq_q.dim() == 2 and seq_k.dim() == 2
    b_size, len_q = seq_q.size()
    b_size, len_k = seq_k.size()
    pad_attn_mask = seq_k.data.eq(0).unsqueeze(1)  # b_size x 1 x len_k
    return pad_attn_mask.expand(b_size, len_q, len_k)  # b_size x len_q x len_k


def get_attention_subsequent_mask(seq):
    assert seq.dim() == 2
    attn_shape = [seq.size(0), seq.size(1), seq.size(1)]
    subsequent_mask = np.triu(np.ones(attn_shape), k=1)
    subsequent_mask = torch.from_numpy(subsequent_mask).byte()
    if seq.is_cuda:
        subsequent_mask = subsequent_mask.cuda()

    return subsequent_mask

class Decoder(nn.Module):
    def __init__(self, n_layers, d_k, d_v, d_model, d_ff, n_heads, max_seq_len, tgt_vocab_size, dropout=0.1, weighted=False):
        # n_layers: Decoder的层数;
        # d_k,d_v：用于计算Attention的K、V的维度;
        # d_model: 模型中间隐藏层的维度;
        # d_ff: FeedForward网络的中间隐藏层的维度;
        # n_head: 多头注意力机制的头数;
        # max_seq_len: 输出文本最大长度;
        # src_vocab_size: 目标语言词表大小;
        super(Decoder, self).__init__()
        self.d_model = d_model
        self.tgt_emb = nn.Embedding(num_embeddings=tgt_vocab_size, embedding_dim=d_model, padding_idx=0)  # 文本嵌入层
        self.pos_emb = PositionEncoding(max_seq_len * 10, d_model)  # 位置编码层
        self.dropout_emb = nn.Dropout(dropout)  # Dropout层
        self.decoder_layer = DecoderLayer if not weighted else WeightedDecoderLayer  # 初始化 Decoder Layer
        self.decoder_layers = nn.ModuleList([self.decoder_layer(d_k, d_v, d_model, d_ff, n_heads, dropout) for _ in range(n_layers)])  # 构建多层 Decoder Layer

    def forward(self, decoder_input_ids, decoder_inputs_len, encoder_input_ids, encoder_outputs, return_attention_weight=False, is_initial=False):
        # 通过文本嵌入层、位置编码层、Dropout层将 decoder_input_ids 进行编码, 将Decoder的序列化的输入文本进行向量化 (batch_size, sen_len) --> (batch_size, sen_len, d_model)
        decoder_inputs = self.dropout_emb(self.tgt_emb(decoder_input_ids) + self.pos_emb(decoder_inputs_len))
        # 计算 Mask
        decoder_self_attention_padding_mask = get_attention_paddiing_mask(decoder_input_ids, decoder_input_ids)  # Transformer 的 Decoder中的 Self-Attention 都需要忽略 padding 部分的影响
        decoder_self_attention_subsequent_mask = get_attention_subsequent_mask(decoder_input_ids)  # Subsequent掩码张量的作用：在transformer中, 掩码张量的主要作用在应用attention时，有一些生成的attention张量中的值计算有可能已知了未来信息而得到的，未来信息被看到是因为训练时会把整个输出结果都一次性进行Embedding，但是理论上解码器的的输出却不是一次就能产生最终结果的，而是一次次通过上一次结果综合得出的，因此，未来的信息可能被提前利用. 所以，我们会进行遮掩.
        decoder_self_attention_mask = torch.gt((decoder_self_attention_padding_mask + decoder_self_attention_subsequent_mask), 0)
        decoder_encoder_attention_padding_mask = get_attention_paddiing_mask(decoder_input_ids, encoder_input_ids)  # Transformer 的 Encoder、Decoder之间的 Attention 需要忽略 padding 部分的影响

        # 用于存放每一层得到的 decoder_self_attention_weights、decoder_encoder_attention_weights
        decoder_self_attention_weights, decoder_encoder_attention_weights = [], []

        # 将decoder_inputs依次经过多层Decoder Layer
        for layer_idx, decoder_layer in enumerate(self.decoder_layers):
            # 第一层decoder_layer是以位置编码层的输出作为输入，之后所有的decoder_layer都是以上一层的decoder_layer的输出作为输入
            if layer_idx == 0:
                decoder_inputs = decoder_inputs
            else:
                decoder_inputs = decoder_outputs

            # decoder_outputs: 经过当前DecoderLayer后得到的输出值 (batch_size, max_tgt_sen_len, d_model)
            # decoder_self_attention_weight: 经过当前DecoderLayer后得到的decoder_inputs的多头自注意力权重 (batch_size, n_head, tgt_sen_len, tgt_sen_len)
            # decoder_encoder_attention_weight: 经过当前DecoderLayer后得到的decoder_inputs与encoder_outputs的多头注意力权重 (batch_size, n_head, tgt_sen_len, src_sen_len)
            decoder_outputs, decoder_self_attention_weight, decoder_encoder_attention_weight = decoder_layer(decoder_inputs=decoder_inputs, encoder_outputs=encoder_outputs, decoder_self_attention_mask=decoder_self_attention_mask, decoder_encoder_attention_padding_mask=decoder_encoder_attention_padding_mask, is_initial=is_initial)

            if return_attention_weight:
                decoder_self_attention_weights.append(decoder_self_attention_weight)
                decoder_encoder_attention_weights.append(decoder_encoder_attention_weight)

        # decoder_outputs: 经过Decoder，得到的输出(batch_size, max_tgt_sen_len, d_model)【max_tgt_sen_len是本batch中最长文本的长度】
        return decoder_outputs, decoder_self_attention_weights, decoder_encoder_attention_weights

3.1 Subsequent mask / 掩码张量【防止标签泄露】

Decoder模块的多头self-attention需要做look-ahead-mask, 因为在预测的时候"不能看见未来的信息", 所以要将当前的token和之后的token全部mask.

掩代表遮掩，码就是我们张量中的数值，它的尺寸不定(大小由传入的size参数决定)，里面一般只有1和0的元素，代表位置被遮掩或者不被遮掩，至于是0位置被遮掩还是1位置被遮掩可以自定义，因此它的作用就是让另外一个张量中的一些数值被遮掩，也可以说被替换, 它的表现形式是一个张量.

Subsequent掩码张量的作用：在transformer中, 掩码张量的主要作用在应用attention时，有一些生成的attention张量中的值计算有可能已知了未来信息而得到的，未来信息被看到是因为训练时会把整个输出结果都一次性进行Embedding，但是理论上解码器的的输出却不是一次就能产生最终结果的，而是一次次通过上一次结果综合得出的，因此，未来的信息可能被提前利用. 所以，我们会进行遮掩.

3.2 Encoder-Decoder attention层

这一层区别于自注意力机制的Q = K = V, 此处矩阵Q来源于Decoder端经过上一个Decoder Block的输出, 而矩阵K, V则来源于Encoder端的输出, 造成了Q != K = V的情况。这样设计是为了让Decoder端的token能够给予Encoder端对应的token更多的关注.

Decoder Block中有2个注意力层的作用: 多头self-attention层是为了拟合Decoder端自身的信息, 而Encoder-Decoder attention层是为了整合Encoder和Decoder的信息.

3.3 解码器层

解码器层的作用：作为解码器的组成单元, 每个解码器层根据给定的输入向目标方向进行特征提取操作，即解码过程。解码器层的最终输出是由”编码器层的最终输出“、”目标数据张量“一同作为解码器层的输入的特征提取结果。

import torch.nn as nn
from transformer.sublayers import MultiHeadAttnAddNormSubLayer
from transformer.sublayers import MultiBranchAttnAddNormSubLayer
from transformer.sublayers import FeedForwardAddNormSubLayer
from transformer.modules import LayerNormalization

class DecoderLayer(nn.Module):
    def __init__(self, d_k, d_v, hidden_size, d_ff, n_heads, dropout=0.1):
        super(DecoderLayer, self).__init__()
        self.decoder_self_attention = MultiHeadAttnAddNormSubLayer(d_k, d_v, hidden_size, n_heads, dropout)
        self.decoder_encoder_attention = MultiHeadAttnAddNormSubLayer(d_k, d_v, hidden_size, n_heads, dropout)
        self.feed_forward = FeedForwardAddNormSubLayer(hidden_size, d_ff, dropout)
        self.layer_norm = LayerNormalization(hidden_size)

    def forward(self, decoder_inputs, encoder_outputs, decoder_self_attention_mask, decoder_encoder_attention_padding_mask, is_initial):
        # decoder_inputs: 表示Decoder端的目标文本序列化后的所有词汇的向量表示(batch_size, tgt_sen_len, d_model)
        # encoder_outputs: 表示Encoder端的最终得到的向量表示(batch_size, src_sen_len, d_model)
        # 因为要做两次attention，所以分了选择
        if is_initial:
            decoder_outputs, decoder_self_attention_weight = self.decoder_self_attention(q=decoder_inputs, k=decoder_inputs, v=decoder_inputs, attention_mask=decoder_self_attention_mask)  # 自注意力机制的Q = K = V (batch_size, sen_len, d_model)
            decoder_outputs, decoder_encoder_attention_weight = self.decoder_encoder_attention(q=decoder_outputs, k=encoder_outputs, v=encoder_outputs, attention_mask=decoder_encoder_attention_padding_mask)  # 这一层区别于自注意力机制的Q = K = V, 此处矩阵Q来源于Decoder端经过上一个Decoder Block的输出, 而矩阵K, V则来源于Encoder端的输出, 造成了Q != K = V的情况
        else:
            decoder_outputs, decoder_encoder_attention_weight = self.decoder_encoder_attention(q=decoder_inputs, k=encoder_outputs, v=encoder_outputs, attention_mask=decoder_encoder_attention_padding_mask)
            decoder_self_attention_weight = None

        decoder_outputs_ = self.feed_forward(decoder_outputs)
        decoder_outputs_ = self.layer_norm(decoder_outputs_ + decoder_outputs)  # add & self.layer_norm
        # decoder_outputs_: (batch_size, max_tgt_sen_len, d_model)
        # decoder_self_attention_weight:(batch_size, n_head, max_tgt_sen_len, )
        return decoder_outputs_, decoder_self_attention_weight, decoder_encoder_attention_weight

import torch
import torch.nn as nn

class LayerNormalization(nn.Module):
    def __init__(self, d_hid, eps=1e-6):
        super(LayerNormalization, self).__init__()
        self.gamma = nn.Parameter(torch.ones(d_hid))
        self.beta = nn.Parameter(torch.zeros(d_hid))
        self.eps = eps

    def forward(self, z):
        mean = z.mean(dim=-1, keepdim=True, )
        std = z.std(dim=-1, keepdim=True, )
        ln_out = (z - mean) / (std + self.eps)
        ln_out = self.gamma * ln_out + self.beta

        return ln_out

3.4 Decoder端的输入解析

Decoder端的架构: Transformer原始论文中的Decoder模块是由N=6个相同的Decoder Block堆叠而成, 其中每一个Block是由3个子模块构成, 分别是多头self-attention模块, Encoder-Decoder attention模块, 前馈全连接层模块.

6个Block的输入不完全相同:

• 最下面的一层Block接收的输入是经历了MASK之后的Decoder端的输入 + Encoder端的输出.
• 其他5层Block接收的输入模式一致, 都是前一层Block的输出 + Encoder端的输出.
• 最底层的Block在训练阶段, 每一个time step的输入是上一个time step的输入加上真实标签序列向后移一位. 具体来看, 就是每一个time step的输入序列会越来越长, 不断的将之前的输入融合进来.
• 最底层的Block在训练阶段, 真实的代码实现中, 采用的是MASK机制来模拟输入序列不断添加的过程.
• 最底层的Block在预测阶段, 每一个time step的输入是从time step=0开始, 一直到上一个time step的预测值的累积拼接张量. 具体来看, 也是随着每一个time step的输入序列会越来越长. 相比于训练阶段最大的不同是这里不断拼接进来的token是每一个time step的预测值, 而不是训练阶段每一个time step取得的groud truth值.

Decoder在训练阶段的输入解析:

• 从第二层Block到第六层Block的输入模式一致, 无需特殊处理, 都是固定操作的循环处理.
• 聚焦在第一层的Block上: 训练阶段每一个time step的输入是上一个time step的输入加上真实标签序列向后移一位. 具体来说, 假设现在的真实标签序列等于"How are you?",
  • 当time step=1时, 输入张量为一个特殊的token, 比如"SOS";
  • 当time step=2时, 输入张量为"SOS How";
  • 当time step=3时, 输入张量为"SOS How are",
  • 以此类推…
• 注意: 在真实的代码实现中, 训练阶段不会这样动态输入, 而是一次性的把目标序列全部输入给第一层的Block, 然后通过多头self-attention中的MASK机制对序列进行同样的遮掩即可.

Decoder在预测阶段的输入解析:

• 同理于训练阶段, 预测时从第二层Block到第六层Block的输入模式一致, 无需特殊处理, 都是固定操作的循环处理.
• 聚焦在第一层的Block上: 因为每一步的输入都会有Encoder的输出张量, 因此这里不做特殊讨论, 只专注于纯粹从Decoder端接收的输入. 预测阶段每一个time step的输入是从time step=0, input_tensor="SOS"开始, 一直到上一个time step的预测输出的累计拼接张量. 具体来说:
  • 当time step=1时, 输入的input_tensor=“SOS”, 预测出来的输出值是output_tensor=“What”;
  • 当time step=2时, 输入的input_tensor=“SOS What”, 预测出来的输出值是output_tensor=“is”;
  • 当time step=3时, 输入的input_tensor=“SOS What is”, 预测出来的输出值是output_tensor=“the”;
  • 当time step=4时, 输入的input_tensor=“SOS What is the”, 预测出来的输出值是output_tensor=“matter”;
  • 当time step=5时, 输入的input_tensor=“SOS What is the matter”, 预测出来的输出值是output_tensor=“?”;
  • 当time step=6时, 输入的input_tensor=“SOS What is the matter ?”, 预测出来的输出值是output_tensor=“EOS”, 代表句子的结束符, 说明解码结束, 预测结束.

4、输出部分

• 线性层
  • 线性层的作用：通过对上一步的线性变化得到指定维度的输出, 也就是转换维度的作用.
• softmax层
  • softmax层的作用：使最后一维的向量中的数字缩放到0-1的概率值域内, 并满足他们的和为1.

---

---

---

参考资料：
Transformer一统江湖：自然语言处理三大特征抽取器比较
The Transformer Family
The Illustrated Transformer
The Annotated Transformer
A Deep Dive Into the Transformer Architecture – The Development of Transformer Models
Transformer图解
Transformer代码阅读
Transformer: A Novel Neural Network Architecture for Language Understanding
图解Transformer（完整版）
NLP 中的Mask全解
Talk to Transformer
Transformer的pytorch实现
基于pytorch的transformer代码实现（包含Batch Normalization，Layer normalization，Mask等讲述）